0 引言

随着20世纪初Bachelier在其博士论文^[1]中引入布朗运动作为风险资产价格变动过程, 微分方程在金融中得到了广泛应用, 如经典的Black-Scholes期权定价模型^[2], Merton的最优投资消费模型^[3]等.近年来, Taksar等人在文献[4]中考虑了精算领域中的几类最优分红模型, 这些模型的求解可归结为求解常微分方程(或者其变分不等式)问题, 且不难求出解的表达式.而对于非稳态问题, 对应的是抛物型方程, 一般不能给出显性解.因此需要用到偏微分程技术对问题的解进行先验估计来定性定量地刻画解和自由边界的性质(见[5-6]).本文的模型来自于文献[4], 但考虑的是有限时间的模型.

在金融领域, 关于梯度约束的抛物型变分不等式在文献[7-10]中已得到一些进展, 解决此类问题的一般方法是把目标函数的变分不等式转化成其梯度的变分不等式, 这样就把梯度约束问题转变成了函数约束问题.但由于本文中遇到的是半无界问题, 如果按上述方法将会产生一个混合边界条件而不方便讨论, 故我们直接对梯度约束的变分不等式进行惩罚逼近来获得解和自由边界的性质.最终我们不仅证明变分不等式$ W^{2, 1}_{p, loc}$解的存在性和上下界, 还通过确定$v_x$、$v_{xx}$、$v_t$、$v_{xt}$的符号, 精确给出并严格证明了自由边界是以0为起点、严格单调递增、$C^\infty $的曲线.

1 金融模型

我们考虑在概率空间$(\Omega, {\cal F}, {\cal F}_t, \mathit{\boldsymbol{P}})$(这里${\cal F}_t$满足通常条件, 即完备且右连续)上的随机最优控制问题.设资产过程$R_s$满足随机过程

$ \begin{eqnarray} \left\{\!\! \begin{array}{l} {\rm d}R_{s}=\mu {\rm d}t+\sigma {\rm d}W_{s}-{\rm d}L_{s}, t\leqslant s\leqslant T, \\ R_{t-}=x, x> 0, \end{array} \right. \end{eqnarray} $

(1)

其中, $W_s$为${\cal F}_s$适应标准布朗运动; $\mu$和$\sigma$为常数, 分别代表风险资产的收益率和波动率; $T $为到期日; $L_s$为${\cal F}_s$适应、单调递增的右连续左极限过程, 代表资产累积分红.我们把所有以$t$时刻作为时间起点的累积分红过程集记为${\cal L}_t$.定义

$ \begin{eqnarray} \tau=\inf\{s\geqslant t:R_s\leqslant0\}. \end{eqnarray} $

(2)

则$\tau$是${\cal F}_s$停时, 代表破产时间.在固定策略$L$下, 至到期日或者破产时的红利贴现的数学期望为

$ {J_{t,x}}(L) = {E_{t,x}}[\int_t^{{T^ \wedge }\tau } {{{\rm{e}}^{ - c(s - t)}}{\rm{d}}{L_s}} ]: = E[\int_t^{{T^ \wedge }\tau } {{{\rm{e}}^{ - c(s - t)}}{\rm{d}}{L_s}|{R_{t - }} = x} ], $

其中常数$c$为贴现因子.模型的目的是寻找最优的分红策略, 使得值函数

$ V(x,t) = \mathop {\sup }\limits_{L \in {L_t}} {J_{t,x}}(L) = \mathop {\sup }\limits_{L \in {L_t}} {E_{t,x}}[\int_t^{{T^ \wedge }\tau } {{{\rm{e}}^{ - c(s - t)}}{\rm{d}}{L_s}} ]. $

(3)

通过动态规划原理(见[11]), 可得到$V$满足以下半无界区域上的变分不等式问题

$ \begin{eqnarray} \left\{\!\! \begin{array}{l} \min\Big\{-V_t-\dfrac{1}{2}\sigma^2V_{xx}-\mu V_x+cV, \;V_x-1\Big\}=0, x>0, 0 < t\leqslant T, \\[2mm] V(0, t)=0, 0 < t\leqslant T, \\ V(x, T)=x, x>0. \end{array} \right. \end{eqnarray} $

(4)

作变换$v(x, t)=V(x, T-t)$, 则$v(x, t)$满足以下变分不等式的初边值问题

$ \begin{eqnarray} \left\{\!\! \begin{array}{l} \min\Big\{v_t-\dfrac{1}{2}\sigma^2v_{xx}-\mu v_x+cv, \;v_x-1\Big\}=0, (x, t) \in (0, \infty)\times(0, T], \\[2mm] v(0, t)=0, 0 < t\leqslant T, \\ v(x, 0)=x, x>0. \end{array} \right. \end{eqnarray} $

(5)

2 值函数的性质

我们将证明问题(5)的解满足:存在$x_\infty>0$(稳态问题的自由边界点), 使得当$x>x_\infty$时, $ v_x\equiv1$(见定理3.5).因此, 只需要考虑以下有界区域问题

$ \begin{eqnarray} \left\{\!\! \begin{array}{l} \min\{v_t-\mathcal{F} v, \;v_x-1\}=0, (x, t)\in Q_T^N:=(0, N)\times(0, T], \\ v(0, t)=0, v_x(N, t)=1, 0 < t\leqslant T, \\ v(x, 0)=x, 0 < x < N, \end{array} \right. \end{eqnarray} $

(6)

其中, $\mathcal{F} v:=\frac{1}{2}\sigma^2v_{xx}+\mu v_x-cv$, $N>x_\infty$为一常数.

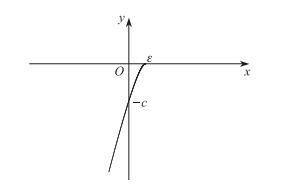
引入惩罚函数$\beta _{\varepsilon}(x)$(见图 1), 满足

$ \begin{eqnarray*} &&\beta _{\varepsilon }(\cdot)\in C^{2}(-\infty, +\infty ), \; \beta _{\varepsilon }(x)\leqslant 0, \\[2mm] &&\beta _{\varepsilon }^{\prime }(x)\geqslant 0, \; \beta _{\varepsilon }^{\prime \prime }(x)\leqslant 0, \;\beta _{\varepsilon}(0)=-c, \\[2mm] &&\lim\limits_{\varepsilon \rightarrow 0}\beta _{\varepsilon }(x)=\left\{\!\! \begin{array}{ll} 0, &x>0, \\ -\infty, &x < 0. \end{array} \right. \end{eqnarray*}% $

考虑惩罚逼近问题

$ \begin{eqnarray} \left\{\!\! \begin{array}{l} v^\varepsilon_t-\mathcal{F} v^\varepsilon+(1+x) \beta _{\varepsilon }(v^\varepsilon_x-1)=0, (x, t)\in Q_T^N, \\ v^\varepsilon(0, t)=0, v^\varepsilon_x(N, t)=1, 0 < t\leqslant T, \\ v^\varepsilon(x, 0)=x, 0 < x < N. \end{array} \right. \end{eqnarray} $

(7)

定理2.1  问题(7)存在解$v^\varepsilon(x, t)\in C^{2, 1}(\overline{Q_T^N}\setminus \{(0, 0)\})\cap C^{1, 0}(\overline{Q_T^N})$, 并且满足

$ \begin{eqnarray} x\leqslant v^\varepsilon\leqslant x+\dfrac{\mu}{c}(1-{\rm e}^{-ct})+\varepsilon\Big(x+\dfrac{\mu}{c}\Big). \end{eqnarray} $

(8)

证明  由Leray-Schauder不动点定理(见[12]), 可以证明问题(7)存在解$v^\varepsilon(x, t)\in C^{1+\alpha, \frac{1+\alpha}{2}}(\overline{Q_T^N})$, 再由Schauder估计(见[13]), 可得$v^\varepsilon(x, t)\in C^{2+\alpha, 1+\frac{\alpha}{2}}(\overline{Q_T^N}\setminus \{(0, 0)\})$.

我们证明式(8)的第一个不等式.令$\phi(x, t)=x$, 则

$ \left\{\!\! \begin{array}{l} \phi_t-\mathcal{F} \phi+(1+x)\beta_{\varepsilon}(\partial_x \phi-1)=-\mu-c\leqslant0, (x, t)\in Q_T^N, \\ \phi(0, t)=0, \partial_x \phi(N, t)=1, 0 < t\leqslant T, \\ \phi(x, 0)=x, 0 < x < N, \end{array} \right. $

由拟线性方程的比较原理(见[14]), $v^\varepsilon\geqslant \phi=x$成立.

再证式(8)的第二个不等式, 令$\Phi(x, t)=x+\frac{\mu}{c}(1-e^{-ct})+\varepsilon(x+\frac{\mu}{c})$, 则

$ \!\! \left\{\!\! \begin{array}{l} \Phi_t-\mathcal{F} \Phi+(1+x)\beta_{\varepsilon}(\partial_x \Phi-1)=c \varepsilon x\geqslant0, (x, t)\in Q_T^N, \\ \Phi(0, t)\geqslant0, \partial_x \Phi(N, t)=1+\varepsilon, 0 < t\leqslant T, \\ \Phi(x, 0)\geqslant x, 0 < x < N. \end{array} \right. $

由比较原理, $v^\varepsilon\leqslant \Phi=x+\frac{\mu}{c}(1-{\rm e}^{-ct})+\varepsilon(x+\frac{\mu}{c})$成立.

性质2.2

$ \begin{eqnarray} v^\varepsilon_x \geqslant 1. \end{eqnarray} $

(9)

证明  对(7)中的方程两边关于$x$求偏导数, 有

$ \begin{eqnarray} \partial_tv^\varepsilon_x-\mathcal{F} v^\varepsilon_x+\beta _{\varepsilon }(v^\varepsilon_x-1)+(1+x)\beta'_{\varepsilon }(v^\varepsilon_x-1)\partial_xv^\varepsilon_x=0. \end{eqnarray} $

(10)

令$w(x, t)\equiv1$, 则

$ \partial_tw-\mathcal{F} w+\beta_\varepsilon(w-1)+(1+x)\beta'_\varepsilon(v^\varepsilon_x-1)\partial_xw=0. $

再由

$ v^\varepsilon_x(0, t)\geqslant1, v^\varepsilon_x(N, t)=1, 0 < t\leqslant T, $

$ v^\varepsilon_x(x, 0)=1, 0 < x < N, $

由比较原理, 得$v^\varepsilon_x\geqslant1$.

性质2.3

$ v^\varepsilon_t\geqslant 0. $

证明  对任意的$h>0$, 令$\widetilde{v}(x, t)=v^\varepsilon(x, t+h)$, 则有

$ \left\{\!\! \begin{array}{l} \partial_t\widetilde{v}-\mathcal{F} \widetilde{v}+(1+x)\beta_{\varepsilon}(\widetilde{v}_x-1)=0, (x, t)\in Q_{T-h}^N, \\[1mm] \widetilde{v}(0, t)=0, \widetilde{v}_x(N, t)=1, 0 < t\leqslant T-h, \\[1mm] \widetilde{v}(x, 0)=v^\varepsilon(x, h)\geqslant x, 0 < x < N.\\ \end{array} \right. $

由比较原理, $\widetilde{v}\geqslant v^\varepsilon$, 即$v^\varepsilon_t\geqslant 0$成立.

性质2.4

$ v^\varepsilon_{xt}\geqslant 0. $

证明  注意到$\widetilde{v}_x$和$v^\varepsilon_x$均满足式(10).又因为$(\widetilde{v}-v^\varepsilon)|_{x=0}=0$, $\widetilde{v}-v^\varepsilon\geqslant0$, 所以$\partial_x(\widetilde{v}-v^\varepsilon)|_{x=0}\geqslant0$.并且$\partial_x(\widetilde{v}-v^\varepsilon)|_{x=N}=0$, $\partial_x(\widetilde{v}-v^\varepsilon)|_{t=0}= v^\varepsilon_x(h, t)-1\geqslant0$.由比较原理, $\widetilde{v}_x\geqslant v^\varepsilon_x$, 即$v^\varepsilon_{xt}\geqslant 0$.

性质2.5

$ v^\varepsilon_{xx}\leqslant 0. $

证明  我们先证明

$ \begin{eqnarray} v^\varepsilon_x(x, t)\leqslant v^\varepsilon_x(0, t), (x, t)\in Q_T. \end{eqnarray} $

(11)

事实上, 比较式(10), $f^\varepsilon(x, t):=v^\varepsilon_x(0, t)$满足

$ \partial_tf^\varepsilon-\mathcal{F} f^\varepsilon+\beta _{\varepsilon }(v^\varepsilon_x-1)+(1+x)\beta'_{\varepsilon }(v^\varepsilon_x-1)\partial_xf^\varepsilon=\partial_tf^\varepsilon+cf^\varepsilon+\beta _{\varepsilon }(v^\varepsilon_x-1), $

由性质2.4、性质2.2, $\partial_tf^\varepsilon\geqslant0$, $f^\varepsilon\geqslant 1$, $\beta _{\varepsilon }(v^\varepsilon_x-1)\geqslant -c$, 故

$ \partial_tf^\varepsilon-\mathcal{F} f^\varepsilon+\beta _{\varepsilon }(v^\varepsilon_x-1)+(1+x)\beta'_{\varepsilon }(v^\varepsilon_x-1)\partial_xf^\varepsilon\geqslant0, $

从而

$ \partial_tf^\varepsilon-\mathcal{F} f^\varepsilon+(1+x)\beta'_{\varepsilon }(v^\varepsilon_x-1)\partial_xf^\varepsilon\geqslant \partial_tv^\varepsilon_x-\mathcal{F} v^\varepsilon_x+(1+x)\beta'_{\varepsilon }(v^\varepsilon_x-1)\partial_xv^\varepsilon_x. $

此外, $f^\varepsilon(0, t)=v^\varepsilon_x(0, t)$, $f^\varepsilon(N, t)\geqslant1= v^\varepsilon_x(N, t)$, $f^\varepsilon(x, 0)=1= v^\varepsilon_x(x, 0)$, 由比较原理, 式(11)成立.

对任意的$h>0$, 令$\overline{v}(x, t)=v^\varepsilon(x+h, t)$, 则在$Q_T^{N-h}$上, $\overline{v}_x$和$v^\varepsilon_x $均满足式(10).又$ (\overline{v}_x-v^\varepsilon_x)|_{x=0}=v^\varepsilon_x(h, t)-v^\varepsilon_x(0, t)\leqslant0$, $(\overline{v}_x-v^\varepsilon_x)|_{x=N-h}=1-v^\varepsilon_x(N-h, t)\leqslant0$, $ (\overline{v}_x-v^\varepsilon_x)|_{t=0}=1-1=0$.由比较原理得, $\overline{v}_x\leqslant v^\varepsilon_x$, 即$v^\varepsilon_{xx}\leqslant 0$.

定理2.6  问题(6)存在唯一解$v(x, t)\in W^{2, 1}_p(Q_T^N)$.

证明   对式(7)式用$L_p$估计(见[13]), 有

$ |v^\varepsilon|_{W^{2, 1}_p(Q_T^N)}\leqslant C(|v^\varepsilon|_{L_p(Q_T^N)}+|\beta_{\varepsilon}(\cdot)|_{L_p(Q_T^N)}+1)\leqslant C_1, $

其中, $ C_1$不依赖于$\varepsilon$.由嵌入定理(见[11]), 当$p>3$时, $W^{2, 1}_p(Q_T^N)\subset\subset C^{1+\alpha, \frac{1+\alpha}{2}}(\overline{Q_T^N})$($\alpha=1- \frac{3}{p}$).故$v^\varepsilon $存在子列, 不妨仍记为$v^\varepsilon$, 以及$v\in W^{2, 1}_{p}(Q_T^N)\cap C^{1+\alpha, \frac{1+\alpha}{2}}(\overline{Q_T^N})$, 使得$v^\varepsilon$在$W^{2, 1}_p(Q_T^N)$中弱收敛, 在$ C^{1+\alpha, \frac{1+\alpha}{2}}(\overline{Q_T^N})$中强收敛于$v$.

下面证明$v$满足(6).由式(7)及式(9)可知

$ v^\varepsilon_t-\mathcal{F} v^\varepsilon\geqslant0, v^\varepsilon_x\geqslant1. $

令$\varepsilon\rightarrow0$可得

$ v_t-\mathcal{F} v\geqslant0, v_x\geqslant1. $

若有$(x, t)\in Q_T^N$使得$v_x(x, t)>1$, 则由$v_x$的连续性及$v^\varepsilon_x$在$Q_T^N$上一致收敛于$v_x$可得, 存在$ \delta>0$, 使得对$(x, t)$的领域$B_\delta$中的任一点$ (y, s)$, 当$\varepsilon < \delta$时有$v^\varepsilon_x(y, s)-1>\delta$, 故在$(y, s)$处$v^\varepsilon_t-\mathcal{F} v^\varepsilon=0$($\varepsilon < \delta$).令$\varepsilon\rightarrow0$可得$v_t-\mathcal{F} v=0$, 因此, $v$满足(6)中的方程.而$v$显然满足(6)中的边界条件, 故$v$是(6)的解.

再证唯一性, 若问题(6)存在两个满足线性增长条件的解$v_1$, $v_2$, 令${\cal N}=\{(x, t):\partial_xv_1>\partial_xv_2\}$, 则在${\cal N}$上有

$ \left\{\!\! \begin{array}{l} {\cal L}_tv_1=0, {\cal L}_tv_2\geqslant0, (x, t)\in {\cal N}, \\ v_1=v_2=0, (x, t)\in\partial_p{\cal N}\cap \{(0, t):t\in \bf{R}\}, \\ \partial_xv_1=\partial_xv_2, (x, t)\in\partial_p{\cal N}\backslash (\{(0, t):t\in \bf{R}\} \cup\{(x, 0):x\in \bf{R}\}\cup\{(x, T):x\in \bf{R}\}), \\ v_1=v_2=x, (x, t)\in\partial_p{\cal N}\cap \{(x, 0):x\in \bf{R}\}, \end{array} \right. $

其中$\partial_p{\cal N}$代表${\cal N}$的抛物边界.由比较原理, $v_2\geqslant v_1$.由此得到

$ \{(x, t):\partial_xv_1> \partial_xv_2\}\subset\{(x, t):v_2\geqslant v_1\}, $

即有

$ C:=\{(x, t):v_2 < v_1\}\subset\{(x, t):\partial_xv_1\leqslant \partial_xv_2\}. $

若$C$非空, 取其一连通分支$D$, 则$D$是一开区域, 在$D$的左边界上有$v_1=v_2$, 而在$D$内部有$\partial_xv_1\leqslant \partial_xv_2$, 由此可得在$D$内部有$v_1\leqslant v_2$, 矛盾.故$C$为空集.同理可证, $\{(x, t):v_1 < v_2\}$为空集.因此, 有$v_1=v_2$成立, 从而证明了问题(6)的解是唯一的.

3 自由边界的性质

根据变分不等式, 定义以下两个区域

$ \hbox{分红区域}: {\cal D}=\{(x, t):v_x=1\}, $

$ \hbox{停止分红区域}: {\cal ND}=\{(x, t):v_x>1\}, $

两者的边界在方程上称为自由边界.由于$v_x$关于$x$单调递减, 于是自由边界可表示成状态变量$x$关于时间$t$的函数$x=d(t)$, 可定义为

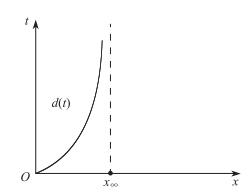
$ d(t):=\inf\big\{x\geqslant0:v_x(x, t)=1\big\}, t\geqslant0. $

关于自由边界, 有以下性质.

定理3.1  $d(t)$单调递增.

证明  由性质2.4, 即$v_x$关于$t$单调递增, 可得结论.

定理3.2  $d(t)$连续, 且$d(0)=0$.

证明  若$d(t)$在$t_0$处不连续, 则由$d(t)$的单调递增性, 有$d(t_0-) < d(t_0+)$.由$ d(t)$的定义及$v_x$的连续性, 有$v_x(d(t_0-), t_0)=v_x(d(t_0+), t_0)=1$.又由$v_x$关于$x$的单调性, 对任意的$x\in (d(t_0-), d(t_0+))$, $v_x(x, d(t_0))=1$, 进而$v_{xx}(x, t_0)=0$.再由$v$满足的方程可得, 对$x\in (d(t_0-), d(t_0+))$, 有$v_{t}(x, t_0)=\mu-cv(x, t_0)$, 进而$v_{tx}(x, t_0)=-cv_x(x, t_0)=-c < 0 $, 这与性质2.4矛盾, 故$d(t)$连续.此外, 由于$v(x, 0)=x$, 即$v_x(x, 0)=1$, 故有$d(0)=0$.

定理3.3   当$t>0$时, $d(t)>0$.

证明  若结论不成立, 则$t_0=\inf\{t\geqslant0:d(t)>0\}>0$, 令$\widetilde{v}(x, t)=v(x, t+t_0)$, 则$ \widetilde{v}$与$v$都满足(6).由解的唯一性有$\widetilde{v}=v$, 即$v$与时间无关, 即$v\equiv x$, 但$v\equiv x$明显不是(6)的解, 矛盾.故结论成立.

为进一步得到自由边界更多的性质, 我们考虑$u=v_x$满足的变分不等式.由于在${\cal ND}$内部, 有$v_t-\mathcal{F} v=0$, 故有$u_t-\mathcal{F} u=0$, 而在${\cal D}$上, $v_t-\mathcal{F} v\geqslant0$, 故在自由边界上有$u_t-\mathcal{F} u=\partial_x(v_t-\mathcal{F} v)\geqslant0$.而在${\cal D}$内部, 由于$u\equiv1$, 容易验证其上$u_t-\mathcal{F} u\equiv c>0$.因此$u$满足函数约束的变分不等式：

$ \begin{eqnarray} \left\{\!\! \begin{array}{l} \min\{u_t-\mathcal{F} u, \;u-1\}=0, (x, t)\in \Omega_T, \\ u(0, t)=f(t), 0 < t\leqslant T, \\ u(x, 0)=1, x>0. \end{array} \right. \end{eqnarray} $

(12)

其中, $f(t)=v_x(0, t)$.

利用文献[15]的方法, 我们可证明以下结论.

定理3.4    $d(t)\in C^\infty((0, \infty))$且严格单调递增.

下面, 我们给出自由边界的上界.

定理3.5    $d(t)$满足

$ d(t) < x_\infty:=\frac{\sigma^2}{\sqrt{\mu^2+2\sigma^2c}}\ln{\frac{\sqrt{\mu^2+2\sigma^2c} +\mu}{\sqrt{\mu^2+2\sigma^2c}-\mu}}, $

这里, $x_\infty$是对应稳态问题的自由边界点.由此可知, 问题(6)的解和问题(5)的解相同.

证明   考虑稳态问题

$ \begin{eqnarray} \left\{\!\! \begin{array}{l} \min\{-\mathcal{F} v, \;v_x-1\}=0, x\in(0, \infty), \\ v(0)=0 \end{array} \right. \end{eqnarray} $

(13)

的解$\widehat{V}$, 满足

$ \widehat{V}(x)=\left\{\!\! \begin{array}{l} C({\rm e}^{\theta_1x}-{\rm e}^{\theta_2x}), 0\leqslant x < x_\infty, \\ C_1+x, x_\infty\leqslant x < +\infty, \end{array} \right. $

其中$\theta_1$、$\theta_2$($\theta_1 < \theta_2$)是特征方程

$ -\frac{1}{2}\sigma^2\theta^2-\mu\theta+c=0 $

的两根.

$ \begin{align*} &x_\infty=\frac{2}{\theta_1-\theta_2}\ln\Big|\frac{\theta_1}{\theta_2}\Big|=\frac{\sigma^2}{\sqrt{\mu^2+2\sigma^2c}}\ln{\frac{\sqrt{\mu^2+2\sigma^2c}+\mu}{\sqrt{\mu^2+2\sigma^2c}-\mu}}, \\ &C=(\theta_1{\rm e}^{\theta_1x_\infty}-\theta_2{\rm e}^{\theta_2x_\infty})^{-1}, C_1=C({\rm e}^{\theta_1x_\infty}-{\rm e}^{\theta_2x_\infty})-x_\infty, \end{align*} $

(见[4]).

这里, 我们也可以把$\widehat{V}$理解为以下抛物型变分不等式的解

$ \left\{\!\! \begin{array}{l} \min\{v_t-\mathcal{F} v, \;v_x-1\}=0, (x, t)\in Q_T^N, \\ v(0, t)=0, v_x(N, t)=1, 0 < t\leqslant T, \\ v(x, 0)=\widehat{V}(x), 0 < x < N. \end{array} \right. $

则由比较原理, 问题(6)的解$v\leqslant\widehat{V}(x)$.又由$v(0, t)=\widehat{V}(0)=0 $, 可得$v_x(0, t)\leqslant\widehat{V}_x(0)$.

而由于$\widehat{V}_x(x)$满足

$ \left\{\!\! \begin{array}{l} \min\{\widehat{V}_t-\mathcal{F} \widehat{V}_x, \;\widehat{V}_x-1\}=0, (x, t)\in Q_T^N, \\ \widehat{V}_x(0, t)=\widehat{V}_x(0)(\geqslant v_x(0, t)), \widehat{V}_x(N, t)=1, 0 < t\leqslant T, \\ \widehat{V}_x(x, 0)=\widehat{V}_x(x)(\geqslant1), 0 < x < N. \end{array} \right. $

由比较原理, 问题(12)的解$u\leqslant\widehat{V}_x(x)$, 故有$\big\{(x, t):v_x(x, t)=1\big\}\supset\big\{(x, t):\widehat{V}_x(x)=1\big\}$, 从而

$ \inf\big\{x\geqslant0:v_x(x, t)=1\big\}\leqslant\inf\big\{x\geqslant0:\widehat{V}_x(x)=1\big\}, $

即$d(t)\leqslant x_\infty$.

4 最优策略及验证定理

在本节中, 我们根据自由边界构造最优策略.令

$ d_T(s)=d(T-t), t\leqslant s < T. $

我们采用如下分红策略$L^{*}_s$.

$ \begin{eqnarray} &&L^{*}_s-L^{*}_{s-}=R^{*}_{s-}-d_T(s), \hbox{如果}\;R^{*}_{s-}>d_T(s), \end{eqnarray} $

(14)

$ \begin{eqnarray} &&{\rm d}L^{*}_s=0, \hbox{如果}\;R^{*}_{s-} < d_T(s). \end{eqnarray} $

(15)

即当$R^{*}_{s-}>d_T(s)$时, 将资产超出$d_T(s)$的部分进行分红, 使$R^{*}$回到自由边界$d_T(s)$上; 而当$R^{*}_{s-}<d_T(s)$时, 采用不分红的策略, 等待资产升值.由此可知, 除起始$t$时刻外, $R^{*}_s$将保持连续且不会越过自由边界, 最终$s\rightarrow T$时收敛于$d_T(T)=0$.下面的定理证明, $L^{*}_s$是最优策略, 而问题(4)的解$V(x, t)$是式(3)所定义的值函数.

定理4.1   设$L^{*}_s$满足式(14)、(15), $V(x, t)$是(4)的解, 则有

$ \begin{eqnarray} &&V(x, t)\geqslant J_{t, x}(L), \forall L_s\in {\cal L}_t, \end{eqnarray} $

(16)

$ \begin{eqnarray} &&V(x, t)= J_{t, x}(L^*). \end{eqnarray} $

(17)

证明  先证明式(16).设$R_s$, $\tau$分别是$L_s$对应的资产过程和破产时间, 由It${\rm{\hat o}}$公式,

$ \begin{align} &V(x,t)={{E}_{t,x}}[{{\rm{e}}^{-c(T\wedge \tau -t)}}V({{R}_{T\wedge \tau }},T\wedge \tau )] \\ &+{{E}_{t,x}}[\int_{t}^{{{T}^{\wedge }}\tau }{{{\rm{e}}^{-c(s-t)}}(-{{V}_{t}}-\frac{1}{2}{{\sigma }^{2}}{{V}_{xx}}-\mu {{V}_{x}}+cV)({{R}_{s}},s)\rm{d}s}] \\ &+{{E}_{t,x}}[\int_{t}^{{{T}^{\wedge }}\tau }{{{\rm{e}}^{-c(s-t)}}{{V}_{x}}({{R}_{s}},s)\rm{d}L_{s}^{c}}]-{{E}_{t,x}}[\sum\limits_{t\le s\le T\wedge \tau }{{{\rm{e}}^{-c(s-t)}}}(V({{R}_{s}},s)-V({{R}_{s-}},s))]. \\ \end{align} $

上式第一、二项非负, 而利用$V_x\geqslant1$, 有

$ \begin{align} &{{E}_{t,x}}[\int_{t}^{{{T}^{\wedge }}\tau }{{{\rm{e}}^{-c(s-t)}}{{V}_{x}}({{R}_{s}},s)\rm{d}L_{s}^{c}}]\ge {{E}_{t,x}}[\int_{t}^{{{T}^{\wedge }}\tau }{{{\rm{e}}^{-c(s-t)}}\rm{d}L_{s}^{c}}], \\ &[V({{R}_{s-}},s)-V({{R}_{s}},s)\ge {{R}_{s-}}-{{R}_{s}}={{L}_{s}}-{{L}_{s-}}, \\ \end{align} $

故有

$ \begin{align*} V(x, t)&\geqslant E_{t, x}\Big[\int_{t}^{{{T}^{\wedge }}\tau }{\rm e}^{-c(s-t)}{\rm d}L^c_s\Big]+E_{t, x}\Big[\sum\limits_{t\leqslant s\leqslant T\wedge\tau}{\rm e}^{-c(s-t)}(L_s-L_{s-})\Big]\\ &=E_{t, x}\Big[\int_{t}^{{{T}^{\wedge }}\tau }{\rm e}^{-c(s-t)}{\rm d}L_s\Big], \end{align*} $

即式(16)成立.

再证明式(17).设$R^*_s$, $\tau^*$分别是$L^*_s$对应的资产过程和破产时间, 由It${\rm{\hat o}}$公式,

$ \begin{align} &V(x,t)={{E}_{t,x}}[{{\rm{e}}^{-c(T\wedge {{\tau }^{*}}-t)}}V(R_{T\wedge {{\tau }^{*}}}^{*},T\wedge {{\tau }^{*}})] \\ &+{{E}_{t,x}}[\mathop{\int }_{t}^{{{T}^{\wedge }}{{\tau }^{*}}}{{\rm{e}}^{-c(s-t)}}(-{{V}_{t}}-\frac{1}{2}{{\sigma }^{2}}{{V}_{xx}}-\mu {{V}_{x}}+cV)(R_{s}^{*},s)\rm{d}s] \\ &+{{E}_{t,x}}[\int_{t}^{{{T}^{\wedge }}\tau }{{{\rm{e}}^{-c(s-t)}}}{{V}_{x}}(R_{s}^{*},s)\rm{d}L_{s}^{*c}] \\ &-{{E}_{t,x}}[\sum\limits_{t\le s\le T\wedge \tau }{{{\rm{e}}^{-c(s-t)}}}(V(R_{s}^{*},s)-V(R_{s-}^{*},s))]. \\ \end{align} $

由于$d_T(T)=0$, 故$R^*_T=0$, 故$R^*_{T\wedge \tau^*}=0$, 从而上式第一项为0.由式(14), $R^*_s$除起点外始终小于$d_T(s) $, 故上式第二项中的被积函数为0.再由式(15), ${\rm d}L^*_s=1_{\{R^*_s=d_T(s)\}}{\rm d}L^*_s, \;s>t$, 而当$ R^*_s=d_T(s)$时, $V_x=1$, 故有

$ V(x, t) =E_{t, x}\Big[\mathop{\int }_{t}^{{{T}^{\wedge }}{{\tau }^{*}}}{\rm e}^{-c(s-t)}{\rm d}L^{*c}_s\Big]-E_{t, x}\Big[\sum\limits_{t\leqslant s\leqslant T\wedge\tau}{\rm e}^{-c(s-t)}(V(R^*_s, s)-V(R^*_{s-}, s))\Big]. $

若$x\leqslant d_T(t)$, 则$L^{*}_s$和$R^{*}_s$始终连续, 故

$ V(x, t) =E_{t, x}\Big[\mathop{\int }_{t}^{{{T}^{\wedge }}{{\tau }^{*}}}{\rm e}^{-c(s-t)}{\rm d}L^{*}_s\Big]; $

若$x> d_T(t)$, 则$V_x(y, t)=1$对$y\in(f_T(t), x)$成立, 且$L^{*}_s$和$R^{*}_s$除起点$t$外始终连续, 故

$ \begin{align*} V(x, t) &=E_{t, x}\Big[\mathop{\int }_{t}^{{{T}^{\wedge }}{{\tau }^{*}}}{\rm e}^{-c(s-t)}{\rm d}L^{*c}_s\Big]-E_{t, x}\Big[V(R^*_t, t)-V(R^*_{t-}, t)\Big]\\[2mm] &=E_{t, x}\Big[\mathop{\int }_{t}^{{{T}^{\wedge }}{{\tau }^{*}}}{\rm e}^{-c(s-t)}{\rm d}L^{*c}_s\Big]-E_{t, x}(R^*_t-R^*_{t-}) \\[2mm] &=E_{t, x}\Big[\mathop{\int }_{t}^{{{T}^{\wedge }}{{\tau }^{*}}}{\rm e}^{-c(s-t)}{\rm d}L^{*c}_s\Big]+E_{t, x}(L^*_t-L^*_{t-}) \\[2mm] &=E_{t, x}\Big[\mathop{\int }_{t}^{{{T}^{\wedge }}{{\tau }^{*}}}{\rm e}^{-c(s-t)}{\rm d}L^{*}_s\Big]. \end{align*} $

综上, 式(17)成立.