0 引言
随着现代科技的发展, 物联网的研究得到了空前发展, 并且变得越来越复杂.对物联网的深入研究最终归结为数学问题.而图的标号问题是20世纪60年代提出的, 它是图论中具有实际应用背景的研究课题, Rosa于1967年提出著名的优美树猜想:每一棵树都是优美树[1]. Marumuthu于2015年首次提出了图的边魔幻优美标号[2], 文献[3]给出具有完全图核心的网络模型可以演变成无标度图(已知每个复杂网络是具有自组织、自相似、吸引子、小世界、无标度中的部分或全部性质的网络).文献[4-9]也给出了几种图标号研究的成果, 文献[10]是对图标号较为全面的综合报道.
本文定义新的图标号, 叫做边魔幻偶优美标号, 研究了具有此类标号的几类图以及这类标号的可封闭性和包含性.给出一种新的添加叶子法, 叫做礼花运算.通过礼花运算, 得到具有边魔幻偶优美标号的可扩散网络模型, 还使得具有边魔幻偶优美标号的图在添加叶子后仍然是边魔幻偶优美的.最后, 把具有边魔幻奇、偶标号的网络模型进行结合, 得到了具有边魔幻优美标号的网络模型.
1 定义与术语
文中论及的图均为无向、简单图, 没有定义的术语和符号参见文献[4].一个$(p, q)$-图是有$p$个顶点和$q$条边的图.为方便起见, 短记号$[m, n]$表示集合$\{m, m+1, m+2, \cdots, n\}$, 其中$m$和$n$均为非负整数; 记号$[s,
t]^e$表示偶数集$\{s, s+2, \cdots, t\}$, 这里的偶数$s$和偶数$t$满足$0 \leq s < t$.定义新的图标号如下.
定义1.1 设$(p, q)$-图$G$有一个映射$f:V(G)
\cup E(G)\rightarrow [0, 2(p+q-1)]^e$, 其中$p=\mid V(G)\mid $,
$q=\mid E(G)\mid $.若存在偶常数$k$, 使对任意边$uv\in E(G)$, 总有$\mid f(u)+f(v)-f(uv)\mid =k$, 则称标号$f$为边魔幻偶优美标号(edge-magic even-graceful labeling), $k$为魔幻常数(magic constant), 图$G$为边魔幻偶优美图(edge-magic even-graceful graph).
定义1.2 设$(p, q)$-图$G_{1}$是初始图.任选图$G_{\mu-1}(\mu-1>1)$的若干片叶子$x_{1}, x_{2},
\cdots, x_{s}$, 给每片叶子$x_{i}$连接新的顶点$y_{i,
1}, y_{i, 2}, \cdots, y_{i, m}$, 得到图$G_{\mu}$.该运算过程叫做礼花运算(firework-operation).在星图上实施多次礼花运算所得到的一类树称为礼花树(firework-tree).
定义1.3 给定$n$个顶点的完全图$K_{n}$和连通图$H_{1}, H_{2}, \cdots,
H_{n}$, 允许某些$H_{j}$没有顶点.完全图$K_{n}$的顶点集合为$V(K_{n})=\{u_{1}, u_{2}, \cdots,
u_{n}\}$, 且每一个$H_{i}(i\in[1, n])$有一个代表顶点$v_{i}\in
V(H_{i})$.对$i\in[1, n]$, 将$H_{i}$的代表顶点$v_{i}
$与完全图$K_{n}$的顶点$u_{i}$重合, 所得到的图叫做以$K_{n}$为基的复合图, 记为$C\langle K_{n} \circ
(H_{1}, H_{2}, \cdots, H_{n})\rangle$.
完全二分图$K_{n, m}$中的特殊图类$K_{1, m}$叫做星, 除星$K_{1, m}$的中心顶点外, $K_{1, m}$的其余顶点为叶子(度数为1的顶点称为叶子).将星$K_{1,
m}$的中心顶点$w_{i}$与完全图$K_{n}$的顶点$u_{i}\in
V(K_{n})=\{u_{1}, u_{2}, \cdots, u_{n}\}$重合, 得到一类重要的网络模型$G=C\langle K_{n} \circ (K_{1, m_{1}}, K_{1,
m_{2}}, \cdots, K_{1, m_{n}})\rangle $, 当$n$和$m_{i}(i\in [1, n])$均在变化时, 网络模型$G$是基于$K_{n}$的网络模型, 其中$K_{n}$构成$G$的核心[3].
2 主要结论及证明
引理2.1 基为$K_{2}$的复合图$C\langle K_{2}
\circ (K_{1, m_{1}}, K_{1, m_{2}})\rangle$是边魔幻偶优美的.
证明 设$K_{2}$的顶点分别为$u_{1, 0},
u_{2, 0}$, 并且$V(K_{1, m_{i}})$=$\{w_{i, 0}, u_{i, 1}, u_{i, 2},
\cdots, u_{i, m_{i}}\}$, 其中$i\in [1, 2]$.将顶点$w_{i, 0}$与顶点$u_{i, 0}$重合后, 得到基为$K_{2}$的复合图$C\langle
K_{2} \circ (K_{1, m_{1}}, K_{1, m_{2}})\rangle$.该复合图的标号如下: $f(w_{1, 0})=0, f(w_{2, 0})=2(m_{1}+2), f(w_{1,
0}w_{2, 0})=2, f(u_{1, i})=2(m_{1}+i+ 2)$和$f(w_{1,
0}u_{1, i})=2+2i, i\in[1, m_{1}]$; $f(u_{2,
j})=4(m_{1}+j)+2$和$f(w_{2, 0}u_{2, j})=4(m_{1}+j+1),
j\in$ $[1, m_{2}]$.经计算, 有
|
$
\begin{align*}
\mid f(w_{1, 0})+f(u_{1, i})-f(w_{1, 0}u_{1, i})\mid &=\mid f(w_{2, 0})+f(u_{2, j})-f(w_{2, 0}u_{2, j})\mid \\
&=\mid 0+2(m_{1}+i+2)-2-2i\mid=2(m_{1}+1).
\end{align*}
$
|
进而导出$f(V(C) \cup E(C))=[0, 2(p+q-1)]^e$.因此,
$f$是一个边魔幻偶优美标号, 复合图$C\langle K_{2} \circ (K_{1,
m_{1}}, K_{1,
m_{2}})\rangle$的边魔幻偶优美性得证.
引理2.2 基为$K_{3}$的复合图$G=C\langle K_{3}
\circ (K_{1, m_{1}}, K_{1, m_{2}}, K_{1,
m_{3}})\rangle$是边魔幻偶优美的.
证明 设$K_{3}$的顶点分别为$u_{1, 0},
u_{2, 0}, u_{3, 0}$, 并且$V(K_{1, m_{i}})\!=\!\{w_{i, 0}, u_{i,
1}, u_{i, 2}, \cdots, u_{i, m_{i}}\}$, 其中$i\in [1,
3]$.将顶点$w_{i, 0}$与顶点$u_{i, 0}$重合后, 就得到基为$K_{3}$的复合图$G=C\langle K_{3} \circ (K_{1,
m_{1}}, K_{1, m_{2}}, K_{1, m_{3}})\rangle$.设$\mid V(G)
\mid=n $, 则$\mid E(G)\mid=n $, $m_{1}+m_{2}+m_{3}=n-3$.定义复合图$G$的标号$g$如下: $g(w_{1, 0})=0,
g(w_{2, 0})=4, g(w_{3, 0})=8, g(w_{1, 0}w_{2, 0})=2, g(w_{2, 0}w_{3,
0})=10$, $ g(w_{1, 0}w_{3, 0})=6=s$, $g(u_{1, 1})=2s, g(w_{1,
0}u_{1, 1})=2(s+1)$, $g(u_{2, 1})=3s, g(w_{2, 0}u_{2, 1})=3s+2$, $
g(u_{3, 1})=3s-2, g(w_{3, 0}u_{3, 1})=3s+4$, $g(u_{1, i})=4(4+i)$,
$g(w_{1, 0}u_{1, i})=4(4+i)+2, i\in[2, m_{1}];$ $g(u_{2,
j})=4(m_{1}+j+3)$, $g(w_{2, 0}u_{2, j})=4(m_{1}+j+3)+2, j\in[2,
m_{2}]$.计算得
|
$
\begin{align*}
\mid g(u)+g(v)-g(uv)\mid &=\mid 4+4(m_{1}+j+3)-4(m_{1}+j+3)-2\mid
\\
&=\mid 4+4(4+i)-4(4+i)-2\mid =2.
\end{align*}
$
|
进而导出$g(V(G) \cup E(G))=[0, 2(p+q-1)]^e$.因此,
$g$是一个边魔幻偶优美标号, 复合图$G= C\langle K_{3}
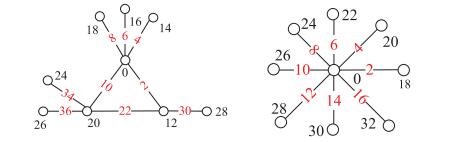
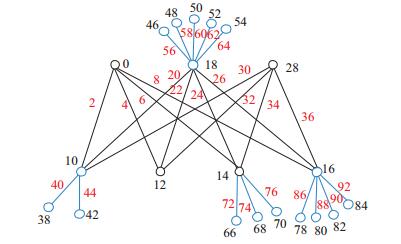
\circ (K_{1, m_{1}}, K_{1, m_{2}}, K_{1, m_{3}})\rangle$的边魔幻偶优美性得证(图 1左图是个边魔幻偶优美的基为$K_3$的复合图).
推论2.3 ⅰ)存在基为$K_{3}$的复合图$G=C\langle
K_{3} \circ (K_{1, m}, K_{1, m}, K_{1,
m})\rangle$是边魔幻偶优美图.
ⅱ)存在基为$K_{3}$的复合图$G=C\langle K_{3} \circ (K_{1, m},
K_{1, m+d}, K_{1, m+2d})\rangle(d\!>\!0)$是边魔幻偶优美图.
ⅲ)存在基为$K_{3}$的复合图$G=C\langle K_{3} \circ (K_{1, m},
K_{1, mq}, K_{1, mq^2})\rangle$$(q>0)$是边魔幻偶优美图.
ⅳ)存在基为$K_{3}$的复合图$G=C\langle K_{2} \circ (K_{1,
m_{1}}, K_{1, m_{2}}, K_{1, m_{3}})\rangle$($m_{1}m_{2}m_{3}=0,
m_{1}+m_{2}+m_{3}\neq 0)$是边魔幻偶优美图.
引理2.4 图$K_{1, n}$是边魔幻偶优美的.
证明 对任意的$k\!\geq\! 5$, 设星图$K_{1,
n}$的中心点为$x$, 叶子上的顶点为$y_{i}$, 点集合$V(K_{1,
n}) =\{x, y_{i}\mid i\in [1, n]\}$, 边集合$E(K_{1,
n})=\{xy_{i}\mid i\in [1, n]\}$.现给出星图$K_{1,
n}$的一个标号如下: $h(x)=0$; $h(y_{i})=k+2i, i\in [1,
n]$; $h(xy_{i})=2i, i\in [1, n]$.由式子$\mid
h(x)+h(y_{i})-h(xy_{i})\mid =\mid k+ 2i-2i\mid
=k$可导出$h(V(K_{1, n}) \cup E(K_{1, n}))=[0, 2k]^e$.所以,
$h$是星图$K_{1, n}$的一个边魔幻偶优美标号, 引理得证(如图 1右图, 图$K_{1,
8}$是边魔幻偶优美的).
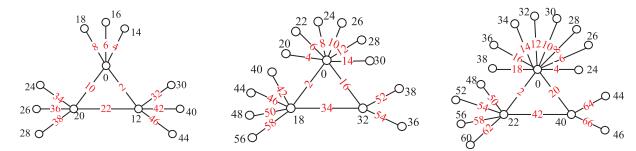
结合礼花运算, 在上述引理的基础上, 可以发现:由基为$K_{3}$的复合图$G$和星图$K_{1,
n}$扩散而得到的网络模型具有边魔幻偶优美标号.故有如下的定理.
定理2.5 存在基为$K_{3}$的复合图$G=C\langle
K_{3} \circ (K_{1, m_{1}}, K_{1, m_{2}}, K_{1, m_{3}})\rangle$的可扩散网络模型具有边魔幻偶优美性.
证明 任意选择复合图$G$(不妨设图$G$为图$G_{1}$)的若干片叶子$x_{1},
x_{2}, \cdots, x_{s}$, 给每片叶子$x_{i}$连接新的顶点$y_{i, 1}, y_{i, 2}, \cdots, y_{i, m}$, 重复任意次, 得到新图$G_{\mu}$.下证新图$G_{\mu}$具有边魔幻偶优美性.由引理2.2可知, 图$G_{1}$是边魔幻偶优美的.按照礼花运算, 任意选择图$G_{\mu-1}$的若干片叶子$x_{1}^{\mu-1}$, $x_{2}^{\mu-1}$, $ \cdots
$, $ x_{s_{l}}^{\mu-1}$, 给每片叶子$x_{s_{r}}^{\mu-1}$($r\in [1,
l]$)连接新的顶点$y_{r, 1}^{\mu}$, $y_{r, 2}^{\mu}$, $ \cdots,
y_{r, m}^{\mu}$.此时, 每片叶子$x_{s_{r}}^{\mu-1}$($r\in [1,
l]$)所连接新的顶点个数$N_{\mu }=\frac{1}{2}[g_{\mu
}(x_{s_{r}}^{\mu-1}y_{r, 1}^{\mu})-g(y_{r,
1}^{\mu})]$由$k(k\geq5)$决定, 则得到图$G_{\mu}$.设由图$G_{1}$到$G_{2}$一直到$G_{\mu-1}$的过程中, 每次连接了$N_{a}$($a\in [2, \mu-1]$)个新的顶点, 设图$G_{\mu-1}$的边和点的个数和为$P_{\mu-1}+Q_{\mu-1}$, 则$P_{\mu-1}+Q_{\mu-1}=\sum_{a=2}^{\mu-1}2N_{a}+k+1$.
假设图$G_{\mu}$是边魔幻偶优美的, 即有图$G_{\mu}$的边魔幻偶优美标号$g_{\mu}$, 使得:
$g_{\mu}(y_{r, {1}}^{\mu})=2(P_{\mu-1}+Q_{\mu-1})$,
$g_{\mu}(x_{s_{r}}^{\mu-1}y_{r, 1}^{\mu})=\mid
g_{\mu}(x_{s_{r}}^{\mu-1})+2(P_{\mu-1}+Q_{\mu-1})-k\mid $, $r\in [1,
l]$; $g_{\mu}(y_{r, m}^{\mu})=2(P_{\mu-1}+Q_{\mu-1}+m)$,
$g_{\mu}(x_{s_{r}}^{\mu-1}y_{r,
m}^{\mu})=g_{\mu}(x_{s_{r}}^{\mu-1}y_{r, 1}^{\mu})+2m$, $m\in [1,
N_{\mu}]$.
下证由图$F_{\mu}$进行礼花运算得到的图$F_{\mu+1}$是边魔幻偶优美的.任意选择图$G_{\mu}$的若干片叶子$y_{1}^{\mu}, y_{2}^{\mu},
\cdots, y_{t_{j}}^{\mu}$, 给每片叶子$y_{t_{w}}^{\mu+1}, w\in [1,
j]$, 连接新的顶点$z_{w, 1}^{\mu+1}, z_{w, 2}^{\mu+1}, \cdots,
z_{w, h}^{\mu+1}$, 每片叶子$y_{t_{w}}^{\mu+1}, w\in [1, j]$, 所连接新的顶点个数$N_{\mu+1}=\frac{1}{2}[g(y_{t_{w}}^{\mu}z_{w,
1}^{\mu+1})-g(z_{w, {1}}^{\mu+1})]$也由$k(k\geq5)$决定, 得到图$G_{\mu+1}$.
设由图$G_{1}$到$G_{2}$一直到$G_{\mu}$的过程中, 每次连接了$N_{a}$($a\in [2, \mu]$)个新的顶点, 设图$G_{\mu}$的边和点的个数和为$P_{\mu}+Q_{\mu}$, 则$P_{\mu}+Q_{\mu}=\sum_{a=2}^{\mu}2N_{a}+k+1$.现给出图$G_{\mu+1}$的一个标号: $g_{\mu+1}(z_{w, {1}}^{\mu+1})=
2(P_{\mu}+Q_{\mu}+1)$, $g_{\mu+1}(y_{t_{w}}^{\mu}z_{w,
1}^{\mu+1})$=$\mid
g_{\mu+1}(u_{t_{w}}^{\mu})+2(P_{\mu}+Q_{\mu}+1)-k\mid$, $w\in [1,
j]$; $g_{\mu+1}(z_{w, h}^{\mu+1})=2(P_{\mu}+Q_{\mu}+h) $,
$g_{\mu+1}(y_{t_{w}}^{\mu}z_{w,
h}^{\mu+1})=g_{\mu+1}(y_{t_{w}}^{\mu}z_{w, 1}^{\mu+1})+2h$, $h\in
[1, N_{\mu+1}]$, 对图$G_{\mu+1}$中由每片叶子与所连顶点得到的任意边$uv\in
E(G_{\mu+1})$以及$w\in [1, j]$, 计算出
|
$
\begin{align*}
&\mid g_{\mu+1}(u)+g_{\mu+1}(v)-g_{\mu+1}(uv)\mid\\
=&\mid g_{\mu+1}(u_{t_{w}}^{\mu})+2(P_{\mu}+Q_{\mu}+h)
-[g_{\mu+1}(u_{t_{w}}^{\mu})+2(P_{\mu}+Q_{\mu}+h)-k]\mid
\\
=&\mid
g_{\mu+1}(u_{t_{w}}^{\mu})-g_{\mu+1}(u_{t_{w}}^{\mu})+2(P_{\mu}+Q_{\mu}+h)-2(P_{\mu}+Q_{\mu}+h)+k
\mid =k,
\end{align*}
$
|
得到$g_{\mu+1}(E(G_{\mu+1}) \cup V(G_{\mu+1}))=[0, 2(p+q-1)]^e$, 其中$p=\mid V(G_{\mu+1})\mid $, $q=\mid E(G_{\mu+1})\mid $.所以,
$g_{\mu+1}$是一个边魔幻偶优美标号, 即图$G_{\mu+1}$是边魔幻偶优美的.
综上, 由数学归纳法可知, 对任意偶数$k(k\!\geq\!5)$, 图$G_{\mu}$的边魔幻偶优美性得证.
定理2.6 存在具有边魔幻偶优美的礼花树$F_{\mu}$.
证明 对任意偶数$k(k\geq5)$, 当${\mu}=1$时, 礼花树$F_{1}$就是星树$K_{1, n}$, 由引理2.4可知,
$f_{1}(x)=0$; $f_{1}(y_{i})=k+2i, i\in [1, n]$; $f_{1}(xy_{i})=2i,
i\in [1, n]$.则有
|
$
\mid f_{1}(x)+f_{1}(y_{i})-f_{1}(xy_{i})\mid =\mid k+2i-2i\mid =k.
$
|
这证得$f_{1}(V(K_{1, n}) \cup E(K_{1, n}))=[0, 2k]^e$.则礼花树$F_{1}$是边魔幻偶优美的.类似地, 由定理2.5, 用数学归纳法可证明, 任意选择礼花树$F_{\mu-1}$的若干片叶子$x_{1}^{\mu-1}$, $x_{2}^{\mu-1}$, $\cdots $, $
x_{s_{l}}^{\mu-1}$, 给每片叶子$x_{s_{r}}^{\mu-1}$($r\in [1, l]$)连接新的顶点$y_{r, 1}^{\mu}$, $y_{r, 2}^{\mu}$, $ \cdots$, $y_{r,
m}^{\mu}$.此时, 每片叶子$x_{s_{r}}^{\mu-1}$($r\in [1, l]$)所连接新的顶点个数$N_{\mu }=\frac{1}{2}[f_{\mu
}(x_{s_{r}}^{\mu-1}y_{r, 1}^{\mu})-f(y_{r,
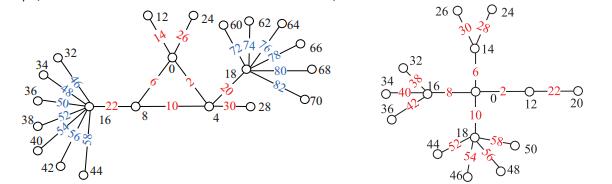
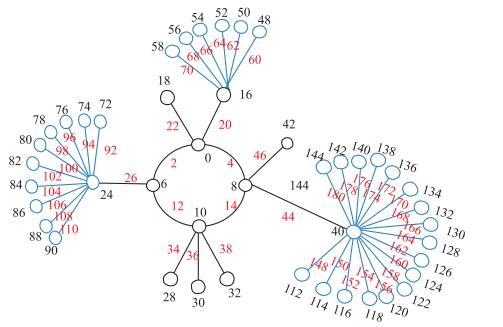
1}^{\mu})]$由$k(k\geq5)$决定, 则得到边魔幻偶优美的礼花树$F_{\mu}$(图 4右图是一个边魔幻偶优美的礼花树).
定理2.7 设$k(k\geq5)$是任意给定常数, $K_{1,
n}$是具有边魔幻奇优美标号的星图, 作$K_{1,
n}$的拷贝$K'_{1, n}$的边魔幻偶优美星图, 连接两颗星树的中心$x_{1}$和$x_{2} $, 所得到的新树具有边魔幻优美标号.任意选择新树的若干叶子进行多次礼花运算所得网络模型也是边魔幻优美的.
证明 由引理2.4可知, 先给出连接星树$K_{1,
n}$和$K'_{1, n}$的中心$x_{1}$和$x_{2} $, 所得到的新树$T$的标号如下: $h(x_{1})=1, h(x_{2})=k+1,
h(x_{1}x_{2})=2, h(y_{1, i})=k+i+1$和$h(x_{1}y_{1,
i})=i+2, i\in[1, k-2]$; $h(y_{2, j})=2(k+j-1)$和$h(x_{2}y_{2,
j})=2(k+i)-1, j\in[1, k-2]$.计算得
|
$
\begin{align*}
\mid h(x_{1})+h(y_{1, i})-h(x_{1}y_{1, i})\mid=\mid h(x_{2})+h(y_{2, j})-h(x_{2}y_{2, j})\mid=\mid 1+k+i+1-i-2 \mid=k.
\end{align*}
$
|
新树$T$的边魔幻优美性得证.任选新树$T$的若干叶子$y_{1,
m}$, $y_{2, n}$$(m\in[1, k-2], n\in[1, k-2])$, 给每片叶子连接新的顶点, 进行礼花运算, 同定理2.5的证明, 可证得该网络模型具有边魔幻优美标号(图 5是一个$k=5$的边魔幻优美的网络模型).
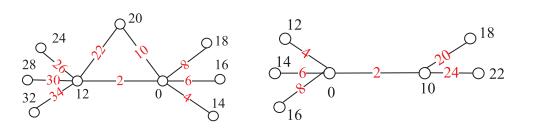
为更好地理解本文的定理, 给出以下2个例子(见图 6和图 7).
和
|
$
\mbox{gph}
D^{(2)}S(\widehat{\mu}, \widehat{x}, \widehat{w}, \widehat{v})=T^{(2)}(\mbox{gph}S, (\widehat{\mu}, \widehat{x}), (\widehat{w}, \widehat{v})).
$
|
因此,
$D(DS(\widehat{\mu}, \widehat{x}))(\widehat{w}, \widehat{v})=D^{(2)}S(\widehat{\mu}, \widehat{x}, \widehat{w}, \widehat{v})$.同理,
$D(DK(\widehat{\mu}, \widehat{x}))(\widehat{w}, \widehat{v})=D^{(2)}K(\widehat{\mu}, \widehat{x}, \widehat{w}, \widehat{v})$.那么, (5)式成立.由于(6)式证明过程与引理3.2相似, 此处省略.
注2.2 (ⅰ)从定理2.3和定理2.4不难发现一个有趣的结论:集值隐函数的相依导数和二阶相依导数仍为相应的集值隐函数.并且从定理2.3到定理2.4能够推得(1)式的集值隐函数的高阶相依导数在相似条件下可以求得.
(ⅱ) $\mbox{gph} S$的凸性可以通过$\mbox{gph} f$的凸性得到.