0 引言

随着科技的发展, 信息流通加速, 尤其是互联网如此普及的今天, 我们的社会进入数据信息极度膨胀的时代, 短时间内产生的数据量, 比人类过去几千年产生的数据量总和还要多.面对海量的数据, 如何有效地处理这些数据显得尤为重要, 而窗口函数就是应对大数据处理的一种解决方案.窗口函数的语法非常简单, 却可以用来代替复杂的子查询语句, 克服了传统的相关子查询的缺点^[1], 可以实现诸如排名(rank)、百分比(percentiles)、移动均值(moving average)、最大值(MAX)、最小值(MIN)以及累积求和(cumulative sums)等相对复杂的操作.

窗口函数作为一种OLAP类型的处理方法, 最早在SQL: 1999^[2]中引入, 在SQL: 2003^[3]中正式规范其标准.窗口函数自被提出之后获得了迅猛的发展, 现在几乎所有的主流数据库均支持窗口函数, 例如Oracle、Microsoft SQL Server、IBM DB2、SAP HANA、PostgreSQL以及Actian VectorWise等.

窗口函数的出现, 使得对数据的操作不再局限于单个元组而是一组特定范围的元组, 但是又不像GROUP BY子句那样只返回一个结果, 窗口函数可以针对每一个元组返回它在整个窗口中的计算结果.运用之前提到的各种分析函数, 就可以实现高效的分析方案, 不仅如此, 实现如此复杂的功能只需要一条非常简单的SQL语句, 降低对于数据库使用者数据处理编程能力的要求.正是基于窗口函数的这些优点, 越来越多的实际应用开始使用窗口函数作为处理数据的手段, 这种趋势在未来还会越来越明显.

例如, 给定一张出租车行车记录表taxi, 包含4个属性: carid、roadid、velocity和time_t. carid是出租车的唯一标识, roadid是每一条路的唯一标识, velocity是出租车的瞬时速度, time_t则是传感器获取速度信息的具体时间, 时间间隔为1 min.下面是一条带Window函数的SQL语句, 表示将所有数据按照路段和出租车ID(Identity)分组, 然后在每个路段上按照时间排序, 选取时间范围前后10 min的最大瞬时速度, 间接反映路况交通信息.

$ \begin{align*} &\bf {SELECT}\\ &~~~~~~~~roadid, carid, time\_t, MAX(velocity)\\ &~~~~~~~~OVER(PARTITION ~BY~ roadid, carid ~ORDER ~BY~ time\_t\\ &~~~~~~~~ROWS~BETWEEN~10~PRECEDING~AND ~10~ FOLLOWING)\\ &{\bf {FROM}} ~taxi; \end{align*} $

尽管窗口函数已经设计的足够精巧, 但是在实际的实现当中, 每个环节仍然没有采用最优化的执行策略, 也就是说整个窗口函数的执行不够高效.在大数据背景下, 这种不够优化的执行策略严重制约着窗口函数的发展, 因此设计出更加优化的执行策略成为当前一个重要的研究课题.

目前主流的商业数据库都不同程度地支持窗口函数, 而且随着版本的升级, 窗口函数的执行策略不断被完善, 例如PostgreSQL在9.4版本之后对窗口函数的执行过程做了改进, 支持朴素聚集、累积聚集以及基于反函数的聚集3种执行策略, 但是最新版本的PostgresSQL依然没有提供对于MIN/MAX函数的优化支持.

窗口的概念并非是数据库领域所独有的, 在数据流处理方面早已引入滑动窗口(sliding window)的概念, 利用滑动窗口保存已经到达的数据, 然后滑动窗口的位置, 实现各类计算.针对数据流领域的滑动窗口, 已经存在很多卓有成效的研究工作:文献[4]在数据流基础上对top- $k$ 问题进行研究; 文献[5]对滑动窗口的语义进行了丰富; 文献[6]则是针对滑动窗口计算存在重叠提出一种改进的优化策略; 文献[7-9]等借鉴消除重复计算的思想, 利用共享计算对滑动窗口的计算过程进行优化.但是滑动窗口和我们讨论的窗口函数应用领域不同, 数据流中很多数据并不能随时访问, 而且数据本身存在不确定性, 对计算的结果并不要求完全准确, 因而很多方法并不能直接在窗口函数中使用, 不过这些优化的思想给我们的优化工作提供了借鉴.

窗口函数执行时, 首先需要进行数据重排序, 然后再执行窗口函数.在重排序阶段, 窗口函数的PARTITION操作与GROUP BY分组操作非常类似, 都是将数据表中的数据按照特定属性划分, 然后对每个组内的元组进行各种数据操作.目前文献[10]针对GROUP BY提出一些新的优化方法, 但是这些方法并不适用于窗口函数.主要因为GROUP BY在整个分组上操作数据返回一个结果, 而窗口函数则保留了原始数据, 并在此基础上计算出额外属性列, 而且窗口函数的语意性更强, 在分组的基础上可以指定任意物理上或逻辑上的窗口大小.在重排序阶段也已经存在一些有效的改进工作, 文献[11]提出了一种基于全排序的重排序方法, 文献[12]则在此基础上提出了更高效的哈希排序和分段排序, 这种排序方法避免相关窗口重复PARTITION和SORT, 提高了单条SQL语句中存在多个窗口函数时的重排序速度.其他更早的排序工作^[13-15], 则从ORDER BY子句和GROUP BY子句中属性关系的角度出发, 针对中间结果的重复利用, 提出了基于函数依赖的排序优化框架.

在窗口函数执行阶段, 文献[16]提出了一种基于segment tree的通用执行框架.文献[17]针对count distinct等窗口聚集函数提出一种改进执行策略.文献[18]则提出了一种基于临时窗口的MIN/MAX优化策略, 通用计算框架适用度固然广泛, 但也决定了它在特定的窗口函数上很难达到最优的执行效果.文献[18]所提的方法虽然比基础的执行策略有了较大的改进, 但是其依然不够完善, 在某些数据分布状态下其效果甚至不如未优化过的执行策略.

本文的工作关注窗口函数的执行阶段, 在文献[18]所提出的方法基础上提出了一种改进的优化策略IM $^{2}$ , 进一步提升了MIN/MAX窗口函数在各类数据分布状态下的执行效率, 并在PostgreSQL中实现该策略, 通过实验验证了其有效性.本文主要贡献点包括以下3点.

(1) 总结窗口函数现有执行策略的局限性, 针对MIN/MAX窗口聚集函数, 提出一种改进的执行算法—— ${\rm IM}^{2}$ .

(2) 详细讨论 ${\rm IM}^{2}$ 算法的空间时间复杂度, 与现有执行策略进行对比分析, 从理论层面证明该算法的有效性, 并采用top- $k$ 策略对该算法相关参数的选取提供指导.

(3) 在PostgreSQL中实现 ${\rm IM}^{2}$ 算法, 采用TPC-H基准测试, 与目前主流的商业数据库SQL Server以及PostgreSQL默认执行策略进行对比实验, 验证 ${\rm IM}^{2}$ 算法的有效性.

本文结构如下:第1节介绍窗口函数现有执行策略; 第2节详细介绍 ${\rm IM}^{2}$ 算法实现过程; 第3节进行实验, 展示与分析结果; 第4节对工作进行总结与展望.

1 窗口函数的执行

本文主要研究的是MIN和MAX窗口函数的执行优化, 这两个函数都属于聚集型的窗口函数, 在标准SQL中, 聚集型窗口函数的通用格式为

$ \text{Agg_func(expression)OVER(}\\ ~~~~~~~~~~\text{[PARTITION BYexpr_list]}\\ ~~~~~~~~~~\text{[ORDER BY order_list [fram_clause]]), } $

其中, Agg_func是一个普通的聚集函数(例如SUM、AVG等), 但在窗口函数中, 聚集函数只作用于当前的窗口, 并为每一个元组返回聚集的结果. OVER子句定义了窗口, 并通过另外3个子句描述窗口的详细内容, 具体如下.

$\bullet$ PARTITION BY子句定义了窗口的分区, 所谓分区就是指将具有相同指定属性值的元组划分在一起.

$\bullet$ ORDER BY子句定义窗口的重排序, 排序的范围被限定在PARTITION所指定的分区内部, 每个分区各自排序, 互相不影响.

$\bullet$ frame_clause定义了边框, 该子句如果缺省则会默认每一个由PARTITION定义的分区即为一个边框. frame_clause的基本形式是ROWS/RANGE BETWEEN p_value AND f_value, 其中p_value定义了边框头与当前元组的位置关系, f_value定义了边框尾和当前元组的关系.目前主要有3种不同的定义模式UNBOUNDED、CURRENT和value PRECEDING/FOLLOWING.

对于每一条元组都可以通过上述的3个子句确定其窗口的位置和大小.标准SQL中有两种确定窗口范围的模式: RANGE模式和ROWS模式.两种模式的区别在于, ROWS是以元组作为比较的单位, 而RANGE则是以值作为比较的单位, 例如某一个聚集窗口函数采用BETWEEN value1 PRECEDING AND value2 FOLLOWING的方式来确定边框, 那么ROWS模式确定边框包含当前元组以及与之相邻的前value1个和后value2个元组, 而RANGE模式确定的边框包括当前元组以及与之相邻的元组中实际值相差在value1至value2的元组.

窗口函数拥有众多不同的计算函数, 但是函数的执行流程大致相同.首先要经过PARTITION和ORDER阶段, 将拥有相同PARTITION值的元组划分到一起, 在每个划分内部按照ORDER BY的值进行排序, 不同分区的排序过程互不影响, 然后是选择相应的执行策略计算窗口函数.

如图 1所示, 整张表先按照奇偶属性进行PARTITION, 所有元组被分成两个分区, 然后在每个分区内部按照ORDER BY属性值的大小排序, 最后通过边框定义子句确定当前边框大小, 当所有的窗口边界被确定下来以后, 便会选择合适的执行策略进行窗口函数的计算.

(1) 朴素聚集策略

该策略的核心思想是针对每一个窗口每次都全部访问所有的元组, 由于相邻窗口之间存在大量重叠, 这种方法就会产生大量重复的工作, 造成其效率低下.但是该方法可用于任何一种聚集函数的计算, 适应性广, 通常被作为最后的选择方案.

(2) 累积聚集策略

该策略在执行时可以重用之前的计算结果, 不需要像朴素策略那样每次扫描全部元组, 实际上聚集策略每次只会扫描尾部新增加的少量元组, 利用上一次计算的结果快速计算出最终结果, 因而非常高效.在这种策略PostgreSQL中被作为首选方案, 但是适应范围有限, 只对边框头不发生改变的窗口函数有效.

(3) 可移除聚集策略

该策略主要用于处理存在反函数的窗口函数, 例如COUNT等函数.执行时首先判断已经聚集过的元组是否依然在当前窗口的范围内, 如果有元组不在其中则调用相对应的反函数将这部分元组剔除, 然后只要再计算新加入的少量元组即可, 因而具有反函数的聚集函数采用该策略拥有较高的效率.

PostgreSQL实现了这三种执行策略, 并根据当前聚集函数的类型决定选择哪种策略去执行.通过上述的讨论分析可知, 像COUNT这种带有反函数的窗口聚集函数以及边框头不变化的窗口函数在PostgreSQL中有着不错的运行效率.但是像MIN/MAX以及其他更为一般的窗口函数只能采用朴素聚集策略, 效率很低.

1.1 PostgreSQL中MIN/MAX窗口函数执行

PostgreSQL中MIN/MAX窗口函数的执行策略采用朴素聚集的方式.为了更好地说明该策略的执行过程, 首先定义窗口的概念.

定义1 由OVER子句定义的包含partition和order by子句以及边框子句所构成的元组集称为一个窗口, 用 $W_i(h, t, V)$ 表示, 其中 $W_i$ 指一个分区中的第 $i$ 个窗口, $h$ 指窗口 $W_i$ 的起始位置, $t$ 指窗口 $W_i$ 的终止位置, $V$ 指窗口 $W_i$ 的转移值, 也就是窗口计算的临时结果.

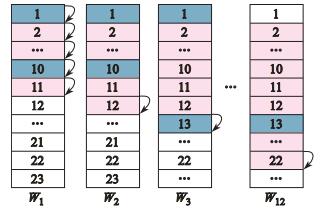
图 2展示了MIN/MAX窗口函数的执行过程, 其中深灰色表示当前进行计算的元组, 浅灰色代表当前窗口范围内的元组, 箭头代表计算当前窗口函数时需要进行读取操作.图中第一个窗口( $W_1$ )起始位置是1, 终止位置是11, 此时需要遍历窗口中的所有元组; 而第二个窗口( $W_2$ )由于起始位置与第一个窗口相比并没有发生变化, 只不过在尾部需要多读取一个新的元组.此时可以利用上次的计算结果, 只需要一次新的元组访问, 随后的10个窗口均是如此; 但是到了第十二个窗口( $W_{12}$ ), 窗口的起始位置发生改变, 则必须重新遍历所有的元组才能计算最终结果, 而且自该窗口之后的窗口都必须重新遍历.

算法1是MIN/MAX窗口聚集函数默认执行策略的伪代码, 其中 $W_i$ 代表分区中的第 $i$ 个窗口, $W_{i}\cdot h$ 表示当前窗口的起始位置, $W_i\cdot t$ 表示当前窗口的结束位置, $W_i\cdot V$ 则表示当前窗口的转移值.首先对于分区中的每一个窗口, 初始化当前窗口的参数 $W_i\cdot h$ 、 $W_i\cdot t$ 和 $W_i\cdot V$ , 并将读指针置于窗口的起始位置(第3行); 然后判断当前窗口的起始位置与前一个窗口起始位置, 如果相等则先将上一次的计算结果存入 $W_i\cdot V$ ; 再后将读指针置于上一个窗口末尾处, 只遍历新加入的元组得到最终的结果值.如果当前窗口起始位置与前一个窗口起始位置不相等则需要重新遍历当前窗口中的所有元组才能计算得到最终结果.

算法1  PostgreSQL MIN/MAX执行算法
输入:经过重排序的表 $T'$ 输出:每个元组所对应的MAX/MIN函数值
1. FOR表 $T'$ 中的每一个分区 $P$ DO 2.  FOR分区 $P$ 中的每一个窗口 3.    初始化 $W_i\cdot h$ 、 $W_i\cdot t$ 、 $W_i\cdot V$ ; 4.  IF $W_i\cdot h==W_{i-1}\cdot h$ THEN 5.     $W_i\cdot V\leftarrow W_{i-1}\cdot V;$ 6.   FOR each row in ( $W_{i-1}{\cdot} t$ , $W_i\cdot t$ ] DO 7.    $W_i\cdot V\leftarrow $ transfunc ( $W_i\cdot V, R_m$ ); 8.   ELSE 9.    FOR each row in [ $W_i\cdot h, W_i\cdot t$ ] DO 10.    $W_i\cdot V\leftarrow $ transfunc ( $W_i\cdot V, R_m$ ); 11.   RETURN $W_i\cdot V$ ;

1.2 代价估算

对于MIN/MAX窗口函数, 当采用类似ROWS BETWEENT value PRECEDING AND value FOLLOWING的方式定义边框时, 除了边界部分窗口可采用累积策略, 多数情况下只能采用朴素聚集策略.

假设当前表拥有 $N$ 条元组, 窗口大小平均是 $T$ , 那么朴素聚集策略每条元组需要重复获取 $T$ 次, 总的计算代价是 $\Theta (NT)$ .计算的代价与窗口的大小和表中总的元组个数的乘积成正比, 原因是朴素聚集策略在窗口头部发生变化时必须重新遍历窗口内所有的元组.

可以看出在这种执行策略之下, 执行瓶颈在于需要重复读取和遍历数据, 即在窗口头部发生变化时, 上一个窗口的计算结果不能被新窗口利用, 而相邻的窗口拥有大量重叠的元组, 因而执行效率不高.

如果MIN/MAX窗口函数采用类似BETWEEN UNBOUNDED PRECEDING and CURRENT ROW的方式定义边框, 那么整个MIN/MAX窗口函数计算可以采用累积策略, 除第一个窗口需要获取全部的元组, 其他窗口每次只需要获取新加入的元组即可, 总的计算代价是 $\Theta(N)$ , 与窗口的大小不再成正比.

综上所述, 除了特殊条件下, MIN/MAX窗口函数的计算代价非常巨大, 与数据规模以及窗口大小的乘积成正比.

2 改进的MIN/MAX窗口函数优化技术——IM $^{2}$

本文前面已经讨论了现有MIN/MAX窗口函数执行策略的瓶颈所在, 本文的优化思路是要记录元组遍历过程中可能会重复使用的元组的信息, 以便多次利用这部分元组, 减少重新遍历所有元组的次数.

2.1 优化执行策略描述

在数据流处理中^[19], SKYLINE指的是在数据中寻找一些特殊位置的数据点, 把这些点用折线连接之后可以覆盖其他所有的数据, 这样的一条折线就是SKYLINE.

如图 3所示, 黑色点代表数据, $Y$ 轴表示数据值的大小, $X$ 轴可以表示时间, 所选取的数据点有个共同特点, 即在它的时间节点之后没有比它更大的点存在, 把所有符合这种特点的数据连接起来就形成一条SKYLINE.本文对SKYLINE模型加以改造, 使其应用于窗口函数计算当中, 新增SKYLINE元组的定义.

定义2 对于MAX函数, 在窗口函数内的元组如果满足在其之后不存在比其大的元组(对于MIN函数则是不存在比其小的元组), 那么称这个元组为SKYLINE元组.

IM $^{2}$ 算法思路是在进行窗口函数计算时, 按顺序存储所有的SKYLINE元组, 这样每当窗口滑动时, 只要剔除滑出当前窗口的SKYLNE元组, 将新加入的SKYLINE元组放到合适的位置, 然后更新SKYLINE元组队列, 并把队列头部的元组作为计算结果返回, 就可以避免对整个窗口的扫描.由SKYLINE元组队列的性质得知, 处于尾部的元组更新频率比较高, 维护成本相应增大, 本文正是基于这种考虑并没有选择保存所有的SKYLINE元组, 而是采取top- $k$ 策略, 只保留最多前 $k$ 个SKYLINE元组, 并通过理论分析和实验验证的方式确定 $k$ 的取值.

为了记录SKYLINE元组的信息, 需要增加数据结构SW. SW结构中包含:一个HEAD数组用来存储被选择元组的位置信息; TAIL记录当前窗口的尾部位置; value数组中存放的是被选择的元组中的值, 该数组与HEAD数组一一对应; actNUM用来记录HEAD和value中有多少个有效的数据; curPOS记录当前排名第一的元组在数组中的下标; maxNUM记录最大能够存储元组信息的个数, 以及一个布尔类型参数flag. SW的数据结构定义如下.

STRUCT SW{

    int HEAD[];   //SKYLINE元组的位置信息

    int TAIL;   //窗口尾部位置

    int value[];   //SKYLINE元组值

    int actNUM;   //有效元组个数

    int curPOS;   //当前在队列头部的元组下标

    int maxNUM;   //最大能存储的SKYLINE元组数量

    bool flag;   //是否要将新元组加入队列

};

如图 4所示, 假设当前maxN=2, 而且当前的聚集函数是MAX.首先第一次遍历窗口 $W_1$ , 找到两个SKYLINE元组(1)和(10), 并用SW结构存储元组信息; 然后计算 $W_2$ 时发现HEAD[curP]所存位置还在当前窗口内部, 表明这个值是有效的, 可以继续使用; 再后比较新元组(12), 发现它比元组(10)要小, 而且actN==maxN, 也就是此时SW没有剩余空间, 则直接忽略.开始计算窗口 $W_3$ , 先判断HEAD[curP]是否在当前窗口内, 假设还是满足的; 然后比较新元组(13)发现它比value[curP]小; 再后从小到大遍历value数组, 比较与元组(13)的大小, 发现value[curP+actN-1] $<$ 元组(13), 则更新SW结构, 将该处替换为元组(13)的信息.之后只要HEAD[curP]标示的位置在当前窗口就一直重复这种操作.

当计算窗口 $W_{12}$ 时, HEAD[curP]已经不在当前窗口范围之内, 则将该值剔除, 顺序扫描HEAD剩下的活跃数据, 直到发现某一HEAD值在当前窗口内的元组为止. 图 4中发现位置(13)的SKYLINE元组满足条件, 则将该元组的值与新元组(22)的值比较返回较大的即可, 这样就避免了重新扫描遍历整个窗口.如果HEAD中没有任何满足条件的值, 那么此时必须重新遍历整个窗口.需要注意的是对于窗口 $W_{12}$ , 如果新元组(22)大于value[curP]则正常更新SW结构, 如果新元组(22)小于value[curP], 虽然此时actN $<$ maxN, 即SW存在剩余空间, 但是却不能存储元组(22), 因为丢失新元组之前的元组信息, 不能确定元组(22)是否应该存入SW.

算法2描述了IM $^2$ MAX窗口函数优化算法, 其中有关窗口表示的相关符号与算法1相同, 这里不再赘述.算法首先对于数据表中的每一个分区, 初始化用于存储SKYLINE元组的SW结构(第2行).对于分区中的每一个窗口, 初始化当前窗口的参数 $W_i\cdot h$ 、 $W_i\cdot t$ 和 $W_i\cdot V$ , 并将读指针置于窗口的起始位置(第4行).

算法2  IM $^{2}$ MAX函数优化算法
输入: PARTITION和ORDER之后的表 $T$ 输出:每个元组所对应的MAX/MIN函数值
1. FOR $T$ 中的每一个分区 $P$ DO 2.   初始化SW结构; 3.    FOR分区 $P$ 中的每一个窗口 $W_i$ DO 4.      初始化 $W_i\cdot h$ 、 $W_i\cdot t$ 、 $W_i\cdot V$ ; 5.        IF $W_i\cdot h==W_{i-1}\cdot h$ THEN 6.         $W_i\cdot V\leftarrow W_{i-1}\cdot V$ ; 7.      FOR rows in ( $W_{i-1}\cdot t, W_i\cdot t$ ) DO 8.         $W_i\cdot V\leftarrow$ transfunc ( $W_i\cdot V, R_m$ ) 9.        IF $W_i\cdot V>{\rm SW}\cdot {\rm value} [{\rm cur}{\rm P}]$ THEN 10.          resetSW $({\rm SW}, \; r_m, \; W_i\cdot V)$ ; 11.        ELSE 12.          updateSW( ${\rm SW}, R_m$ ); 13.      SW.TAIL $\leftarrow W_i\cdot t$ ; 14.      ELSE IF $W_i\cdot h\leq {\rm SW}\cdot {\rm HEAD}\lceil {\rm curP} \rceil$ THEN 15.         $W_i\cdot V\leftarrow {\rm SW.value}[{\rm curP}]$ ; 16.        FOR rows in ( ${\rm SW}.{\rm TAIL}, W_i\cdot t$ )DO 17.           $W_i\cdot V\leftarrow$ transfunc( $W_i\cdot V$ , $R_m$ ); 18.          IF $W_i\cdot V>{\rm SW}.{\rm value}[{\rm cur P}]$ THEN 19.           resetSW( ${\rm SW}, \; r_m, \;W_i\cdot V$ ) 20.        ELSE 21.          updateSW( ${\rm SW}, R_m$ ); 22.      SW.TAIL $\leftarrow W_{i}, t$ 23.    ELSE IF $W_k\cdot h\leq {\rm SW}.{\rm HEAD}\lceil {\rm curP}+{\rm actN}-1 \rceil$ 24.    THEN 25.      SW.curPOS $\leftarrow {\rm findpos} ({\rm SW}, \;W_i\cdot h);$ 26.       $W_i\cdot V\leftarrow {\rm SW}.{\rm value}\lceil {\rm curP}\rceil$ 27.      FOR rows in ( ${\rm SW}.{\rm TAIL}, \;W_i\cdot t$ )DO 28.         $W_i\cdot V\leftarrow$ transfunc( $W_i\cdot V, \; R_m$ ); 29.        IF $W_i\cdot V>{\rm SW.value}\lceil {\rm curP} \rceil$ THEN 30.          resetSW $({\rm SW}, \;r_m, \;W_i\cdot V)$ 31.        ELSE 32.          updateSW( ${\rm SW}, \;R_m$ ); 33.      SW.TAIL $\leftarrow W_i\cdot t$ 34.    ELSE 35.      FOR each row in [ $W_i\cdot s, \;W_i\cdot e$ ]DO 36.       $W_i\cdot V\leftarrow $ transfunc( $W_i\cdot V, \;R_m$ ); 37.      IF $W_i\cdot TV>{\rm SW.value}\lceil {\rm curP} \rceil$ THEN 38.        resetSW $({\rm SW}, \;r_m, \;W_i\cdot V)$ 39.      ELSE 40.         updateSW( ${\rm SW}, \;R_m$ ); 41.      SW.TAIL $\leftarrow W_i\cdot t$ 42.    RETURN $W_i\cdot TV$ ;

当前窗口的起始位置与上一个窗口的起始位置相比, 如果位置相同, 则只需遍历与上一个窗口相比新增的元组, 如果新的元组大于SW中最大的SKYLINE元组则重置SW结构, 只保存新元组的信息, 并把新元组的值作为最终计算结果.与此同时, 如果新元组小于SW中最大SKYLINE元组, 则更新SW结构(第12行), 把SW中已存最大值作为最终计算结果.所有元组遍历结束后更新SW的结束位置(第13行).

如果起始位置不相同, 则比较当前窗口的起始位置与SW中所存最大元组的起始位置; 如果当前窗口的起始位置不大于SW所存最大SKYLINE元组的起始位置, 首先将SW存储的最大SKYLINE元组值赋予当前窗口的转移值, 并遍历从SW记录的窗口的终止位置到当前窗口的终止位置处的元组及计算相应的转移值.与此同时, 如果每次新元组大于SW的最大SKYLINE元组则重置SW结构, 否则就执行更新操作, 所有元组遍历结束后更新SW的结束位置(第14-22行); 如果当前窗口的起始位置大于SW所存最大SKYLINE元组的起始位置, 则对SW中已存的所有SKYLINE元组进行二分查找, 找到一个满足条件元组, 将该元组值赋值给当前窗口的转移值, 并把在其之前的失效SKYLINE元组剔除, 剩余操作与前一种情况一致(第23-33行).

如果SW结构中没有满足条件的元组, 则遍历窗口内的所有元组, 并计算其相应的转移值.与此同时, 实时重置或者更新SW结构.所有元组遍历结束后更新临时窗口的结束位置(第34-41行).

算法中resetSW函数处理新的SKYLINE元组比任何已经存储的SKYLINE都大的情况, 此时只保存新元组的相关信息即可. updateSW函数则在新元组到来时负责更新SW结构, 核心思想是将新元组与SW已经存的元组进行排名, 剔除排名在新元组之后元组, 如果有剩余空间, 则将新元组信息添加进SW结构.当然并非存在剩余空间时都可以添加数据, 因为算法并没有保存所有的SKLINE元组.假设SW结构已满, 并且新来的元组没有添加到SW, 当某一时刻满足算法第23行的判断条件, 选取元组之后, 失效的元组被剔除, 此后若新元组到来排名却在最后, 虽然存在剩余空间却不能将其添加到SW, 因为已经丢失了很多在新元组之前元组信息.为了准确判断是否更新SW还需要借助SW中的flag变量.

2.2 算法复杂度分析

假设存储窗口内所有的SKYLINE元组个数为 $k$ , 并且数据服从均匀分布, 那么每次有新元组到来只需要与已有的SKYLINE元组进行排序.已存储的元组是有序排列的, 因而此时排序问题变成二分查找插入问题, 插入新元组之后再将排在新元组之后的SKYLINE元组删除即可.该过程的复杂度为 $\Theta(\log k)$ , 对于拥有 $N$ 个元组的表, 整个窗口函数的执行复杂度为 $\Theta(N\log k)$ .

假设当前数据中每个元素从均匀分布中随机独立选取, 而对于 $n$ 个元组中的第 $i$ 元组满足SKYLINE条件的概率为

$ \int_0^1 {{p^{n - i}}{\text{d}}p = \frac{1}{{n - i + 1}}} $

(1)

对于一个大小为 $T$ 的窗口, SKYLINE值的期望个数为

$ \begin{align} \sum\limits_{i = 1}^Y {\int_0^1} T^{n-i}{\text d}T=1+\dfrac{1}{2}+\cdots +\dfrac{1}{T}\approx \ln T. \end{align} $

(2)

公式(2)的含义是, 如果数据服从均匀分布, 需要全部存储SKYLINE元组个数的期望是 $\Theta (\log T)$ , 然而存储全部SKYLINE元组并非最好的策略, 因为SKYLINE元组排名越靠后, 被替换更新的可能性就越大, 而其被利用的可能性越小, 即存储排名靠后的元组收益不高, 从复杂度 $\Theta(N \log k)$ 也可以看出, 当假设条件全部成立时复杂度与 $k$ 正相关.

本文采用top- $k$ 策略, 选取前 $k$ 个SKYLINE元组保存下来, $k$ 的选取会根据窗口的大小 $T$ 来决定, 取值介于1和 $\Theta(\log T)$ 之间.这种策略没有存储所有的SKYLINE元组, 存在元组全部失效的可能性, $k$ 取值越小, 失效的可能性越大, 一旦全部失效需要重新遍历窗口, 因而 $k$ 的取值不能太小, 实验发现 $k$ 取 $\log T/2$ 左右效果最好.

3 实验结果与分析 3.1 实验环境

本文的实验环境为一台联想90AU0010CP台式电脑, 该电脑拥有英特尔第四代酷睿i5-4460@3.20GHz四核CPU, 8GB DDR3L 1600MHz的内存.实验所用数据库包括PostgreSQL9.4.4和Microsoft SQL Server 2012(Standard Edition), 并修改了PostgreSQL的源代码, 实现本文提出的IM $^{2}$ 优化算法.实验中所有数据库工作内存被设置为500 MB.

3.2 实验内容

实验使用的数据来自TPC-H基准测试, 通过TPC-H的数据生成工具DBGEN生成两张张MYORDER测试表, 其中一张是包含1 500 000条元组, 数据大小为170 M, 另外一张包含15 000 000条元组, 大小为1.7 GB.本文实验使用如下两条SQL语句进行测试, 两条语句ORDER属性不同, 用于产生不同的数据分布.

SQL-1:

SELECT

o_totalprice, MAX(totalprice)

OVER(ORDER BY o_orderkey ROWS)

       BETWEEN val PRECEDING AND val FOLLOWING

FROM myorder;

SQL-2:

SELECT

o_totalprice, MAX(o_totalprice)

OVER(ORDER BY o_totalprice DESC ROWS

       BETWEEN val PRECEDING AND val FOLLOWING)

FROM myorder;

3.3 对比实验简介

$\bullet$ PG: PostgreSQL默认执行算法

$\bullet$ SQLServer: SQLServer 2012 (Standard Edition)

$\bullet$ TW:该方法发表在计算机学报2016, 作为baseline

$\bullet$ IM $^{2}$ : top- $k$ IM $^{2}$ 优化算法

3.4 实验结果

首先比较的是PostgreSQL默认执行策略、SQL Server默认执行策略以及本文提出的IM $^{2}$ 执行策略, 结果如图 5所示.在执行相同的SQL语句时, IM $^{2}$ 算法的执行效率比普通商业数据的默认执行算法高很多, 而且可以发现PostgreSQL和SQL Server在计算MAX聚集窗口函数时采用的是朴素聚集的方法, 在数据量一定的前提下, 执行时间与窗口大小成正比, 图中蓝色和红色两条线也印证了这一点.本文提出的IM $^{2}$ 算法则有着巨大的优势, 窗口大小的变化对执行时间影响很小, 一直维持较高的执行效率.

图 6展示的是IM $^{2}$ 算法在不同的 $k$ 值下的执行时间, 图中展示的是 $k$ =1、 $k$ =5和 $k$ =8时的结果.实验结果去除了SQL语句编译以及重排序阶段, 只对比窗口函数执行期间的时间消耗.需要说明的是, 当 $k$ =1时, 本文的IM $^{2}$ 算法退化为文献[18]提出的TW算法.从图中可以明显地看出, 本文提出的IM $^{2}$ 算法在 $k$ 取值大于1时, 比TW算法大约提升了10%的效率; 同时也可以看出, 并非 $k$ 取值越大越好, 图中IM $^{2}$ -5的效率要高于IM $^{2}$ -8, 也就是说存储过多的备选元组, 增加了维护这部分数据的时间代价, 从而降低执行的效率, 因此 $k$ 的值不宜过大. 图 7则是在1.7 GB数据下进行的实验, 此时 $k$ 取值为1、3、5, 我们发现本文提出的IM $^{2}$ 算法依然比TW算法存在优势.

图 8展示的是采用不同 $k$ 值的IM $^{2}$ 算法与PostgreSQL默认执行策略在SQL-2上的执行时间.可以看出TW(IM $^{2}$ -1)算法此时和PostgreSQL的默认算法基本重合, 甚至不及默认算法, 这是因为当数据逆序排列时, TW算法失效, 而且由于其需要维护额外的数据结构, 因而比PostgreSQL的默认算法执行速度慢.在这种情况下, 本文的IM $^{2}$ 算法在 $k$ 值大于1时有着明显的优势, 而且 $k$ 取值越大, 优化效果越明显, 但是随着 $k$ 值增大, 优化效果的增长越来越不明显, 鉴于图 7的实验结果, $k$ 值比较大时, 在其他数据分布条件下反而效率不高, 因而 $k$ 的取值不宜过大. 图 9则是在1.7 GB的数据集上进行的实验, 此时 $k$ 取值分别为1、3、5, 可以发现在数据量变大之后, IM $^{2}$ 算法依然能保持其高效性.

图 10展示窗口大小为1 000时, $k$ 值的选取与优化效果的关系, 此时SKYLINE元组的期望是8, 可以发现随着 $k$ 增大, 执行时间呈现出先降后增的趋势, 进一步说明之前的分析, $k$ 并非越大越好, 而且可以发现 $k$ 在取期望值一半时优化效果比较好.

4 总结与展望

本文通过对窗口函数的执行过程进行分析, 发现现有执行算法的瓶颈所在, 针对MIN/MAX窗口聚集函数提出一种改进的执行算法——IM $^2$ , 该算法通过预存储多个临时值的方式避免重复计算, 达到优化的目的.从理论和实验两个方面验证了该算法的有效性, 并在PostgreSQL中实现了IM $^{2}$ 算法.

本文的工作依然存在不足, IM $^{2}$ 算法并非一种通用的执行策略, 不能用于除MIN/MAX之外的其他聚集函数, 在未来的工作中, 我们将基于现有的工作, 结合文献[16]的方法, 继续改进算法, 从而将该算法应用到通用执行框架中.