行波在生物种群领域中一直以来可以很好地反映种群在时空中的分布情况, 特别是在诠释入侵种群在空间的传播方面得到了很好应用.由于在现实世界中种群的分布受多种因素的制约, 比如种群内相互作用的反应时滞因素, 许多生物数学学者也着手研究时滞反应扩散方程中行波解的存在性问题.文献[1]利用上下解的理论和单调迭代的方法讨论了一类带离散时滞的反应扩散方程中波前解的存在性; 文献[2]还进一步发现时滞还可以导致慢行波解的出现.当种群模型中的时滞表现为分布时滞的时候, 文献[3-6]借助改进上下解和单调迭代方法讨论了一些带非局部时滞或者时空滞后反应扩散方程中波前解的存在性问题.此外, 文献[7]借助几何奇异摄动理论[8]还讨论了时空滞后效应下种群模型中行波解的存在性问题, 指出在小时滞情况下该行波解的存在条件, 但是并未考虑随着时滞的增加该行波解的动力学行为将如何变化.关于行波解动力学行为方面的研究还主要集中在种群模型为反应扩散方程或者带空间非局部效应的反应扩散方程的情况.例如, 文献[9]对两变量的反应扩散方程中行波解的动力学行为做了大量的研究, 指出当描述种群的反应扩散方程的反应方程存在超临界的Hopf分支时, 行波解的动力学会发生一些变化.具体地讲, 当系统的反应方程发生超临界的Hopf分支时, 会导致系统出现一族周期解.
对于存在时空时滞的种群模型, 最早是由英国的生物数学家Britton提出[10], 且时滞对该种群模型的行波解的影响很少有人关注.本文主要在该模型的基础上考虑如下形式的种群模型
| $ u_t =d\Delta u+ru(1+\alpha u-\beta u^2-(1+\alpha -\beta )(f\ast \ast u)), $ | (1) |
其中
| $ (f\ast \ast u)(x, t)=\int_{-\infty }^t {\int_{\textbf{R}} {f(x-y, t-s)u(y, s){\rm d}y{\rm d}s} }, \quad f(x, t)=\frac{1}{\sqrt {4\pi t} }{\rm e}^{-\frac{\left| x \right|^2}{4t}}\frac{1}{\tau }{\rm e}^{-\frac{t}{\tau }}, $ |
在本节中, 主要关注模型(1)在时空滞后项的条件下, 其波前解的存在性.为了研究方便, 令
| $ \left\{\!\! {\begin{array}{l} u_t =\Delta u+f_1 (u, v), \\ v_t =\Delta v+f_2 (u, v), \\ \end{array}} \right. $ | (2) |
其中
| $ \begin{align*} &f_1 (u, v)=ru(1+\alpha -\beta u^2-(1+\alpha -\beta )v), \\ &f_2 (u, v)=\frac{1}{\tau }(u-v). \end{align*} $ |
下面利用几何奇异摄动理论证明系统(2)在时滞
情况1 当
| $ u_t =\Delta u+ru[1+\alpha u-\beta u^2-(1+\alpha-\beta )u]. $ | (3) |
系统(3)的行波解有如下的形式
| $ u(x, t)=\varphi (z), \quad z=x+ct, $ |
其中
| $ c{\varphi }'={\varphi }''+r\varphi [1+\alpha \varphi-\beta \varphi ^2-(1+\alpha-\beta )\varphi], $ | (4) |
并且满足如下的边界条件:
对于系统(4), 我们有如下的结论:
定理1.1 如果
证明 首先, 令
| $ \left\{\!\! {\begin{array}{l} {\varphi }'=\phi, \\ {\phi }'=c{\varphi }'-r\varphi [1+(\beta-1)\varphi-\beta \varphi ^2]. \\ \end{array}} \right. $ | (5) |
系统(5)有三个平衡点(0, 0), (1, 0),
为了证明连接平衡点(0, 0)和(1, 0)的异宿轨道的存在性, 需要先证明对合适的
| $ B=\left\{ {(\varphi, \phi ):0\le \varphi \le 1, 0\le \phi \le \lambda \varphi } \right\}, $ |
是负向不变集.也就是对该三角集合
| $ \begin{align*} f\cdot n&=(\phi, c\phi +r\varphi [1+(\beta-1)\varphi-\beta \varphi ^2])\cdot (\lambda, -1)\left| {_{(\varphi, \lambda \varphi)}}\right. \\ &=\varphi [\lambda ^2-c\lambda +r(1+(\beta-1)\varphi-\beta \varphi ^2)] \\ &\le \varphi \Big[\lambda ^2-c\lambda +r\frac{(\beta +1)^2}{4\beta }\Big]. \end{align*} $ |
这样当
从上面的分析知道, 对于鞍点(1, 0)而言, 总存在一个不稳定流形分枝, 使得系统(5)有沿该不稳定流形又连接平衡点(0, 0)和(1, 0)的异宿轨道存在.
情况2 当
| $ \left\{\!\!{\begin{array}{l} {\zeta }''-{\zeta }'+r\zeta [1+\alpha \zeta-\beta \zeta ^2-( 1+\alpha-\beta )\xi]=0, \\[2mm] {\xi }''-c\xi +\dfrac{1}{\tau }(\zeta -\xi )=0, \\ \end{array}} \right. $ | (6) |
并且满足边界条件
| $ \zeta (-\infty )=0, \quad \zeta (+\infty )=1, \quad \xi (-\infty )=0, \quad \xi (+\infty )=1. $ |
为了得到(6)的解, 我们需要令
| $ \left\{\!\! {\begin{array}{l} {\zeta }'=\widetilde {\zeta }, \\ {\widetilde {\zeta }}'=c{\zeta }'-r\zeta [1+\alpha \zeta-\beta \zeta ^2-(1+\alpha-\beta )\xi], \\ {\xi }'=\widetilde {\xi }, \\[2mm] {\widetilde {\xi }}'=c{\xi }'-\dfrac{1}{\tau }(\zeta -\xi ), \end{array}} \right. $ | (7) |
显然, 系统(7)有两个平衡点(0, 0, 0, 0)和(1, 0, 1, 0).
若引进小参数
| $ \left\{\!\! {\begin{array}{l} {u}'=\widetilde {u}, \\ {\widetilde {u}}'=c\widetilde {u}-ru[1+\alpha u-\beta u^2-(1+\alpha -\beta )v], \\ \varepsilon {v}'=\widetilde {v}, \\ \varepsilon {\widetilde {v}}'=\varepsilon c\widetilde {v}-(u-v). \\ \end{array}} \right. $ | (8) |
值得注意的是, 当
| $ z=\varepsilon \eta . $ |
在此变换下, 系统(8)变为
| $ \left\{\!\! {\begin{array}{l} {u}'=\varepsilon \widetilde {u}, \\ {\widetilde {u}}'=\varepsilon c\widetilde {u}+\varepsilon ru[1+\alpha u-\beta u^2-(1+\alpha-\beta )v], \\ {v}'=\widetilde {v}, \\ {\widetilde {v}}'=\varepsilon c\widetilde {v}+(v-u). \end{array}} \right. $ | (9) |
系统(9)通常称为快变系统.需要注意的是, 当
当
| $ M_0 =\left\{ {(u, \widetilde {u}, v, \widetilde {v})\in {\textbf{R}}^4:\widetilde {v}=0, u=v} \right\}. $ |
如果此2维不变流形
再结合Feniche的理论, 我们知道要得到系统(8)的双曲性, 就必须使得系统(9)的线性化部分的特征值在虚轴上的个数恰好等于流形
| $ \left({\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ {-1} & 0 & 1 & 0 \\ \end{array} }\right). $ |
显然, 上面的矩阵的4个特征值分别为0、0、1、
| $ M_\varepsilon =\{(u, \widetilde {u}, v, \widetilde {v})\in {\textbf{R}}^4:\widetilde{v}=g(u, \widetilde {u}, \varepsilon ), v=u+h( u, \widetilde {u}, \varepsilon)\}, $ |
其中函数
| $ g(u, \widetilde {u}, 0)=h(u, \widetilde {u}, 0)=0. $ | (10) |
于是, 函数
| $ g(u, \widetilde {u}, \varepsilon )=\varepsilon g_1 +\varepsilon ^2g_2 +\cdots, \quad h(u, \widetilde {u}, \varepsilon )=\varepsilon h_1 +\varepsilon ^2h_2 +\cdots . $ | (11) |
从上面的分析, 我们知道系统(8)在不变流形
| $ \Big(1+\frac{\partial h}{\partial u}\Big){u}'_z +\frac{\partial h}{\partial \widetilde {u}}{\widetilde {u}}'_z ={v}'_z . $ | (12) |
把式(12)带入系统(8), 并限制在流形
| $ \varepsilon \Big[\Big(1+\frac{\partial h}{\partial u}\Big)\widetilde {u}+\frac{\partial h}{\partial \widetilde {u}}(c\widetilde {u}-ru-\alpha ru^2+\beta ru^3+(1+\alpha-\beta )ru(u+h))\Big]=g. $ | (13) |
同时结合
| $ \varepsilon \Big[\frac{\partial g}{\partial u}\widetilde {u}+\frac{\partial g}{\partial \widetilde {u}}(c\widetilde {u}-ru-\alpha ru^2+\beta ru^3+(1+\alpha-\beta )ru(u+h))\Big]=c\varepsilon g+h. $ | (14) |
再把式(11)带入式(13)和式(14), 整理比较关于
| $ \begin{align*} &g_1 (u, \widetilde {u})=\widetilde {u}, \quad g_2 (u, \widetilde {u})=0, \\ &h_1 (u, \widetilde {u})=0, \quad h_2 (u, \widetilde {u})=-ru-\alpha ru^2+\beta ru^3+(1+\alpha -\beta )ru^2. \end{align*} $ |
这样, 我们可以得到函数
| $ g(u, \widetilde {u}, \varepsilon )=\varepsilon \widetilde {u}+o( \varepsilon ), \\ h(u, \widetilde {u}, \varepsilon )=(-ru-\alpha ru^2+\beta ru^3+(1+\alpha -\beta )ru^2)\varepsilon ^2+o(\varepsilon ^2). $ | (15) |
有了函数
| $ \left\{\!\! {\begin{array}{l} {u}'_z =\widetilde {u}, \\ {\widetilde {u}}'_z =c\widetilde {u}-ru-\alpha ru^2+\beta ru^3+(1+\alpha -\beta )ru(u+h), \\ \end{array}} \right. $ | (16) |
其中
| $ \left\{\!\! {\begin{array}{l} u=u_0 +\varepsilon ^2u_1 +\cdots, \\ \widetilde {u}=\widetilde {u}_0 +\varepsilon ^2\widetilde {u}_1 +\cdots, \end{array}} \right. $ | (17) |
把式(17)带入系统(16)得到关于
| $ \frac{\rm d}{{\rm d}z}\left({\begin{array}{*{20}c} {u_1 } \\ {\widetilde {u}_1 } \\ \end{array} }\right)+\left({\begin{array}{*{20}c} 0 & {-1} \\ {G(u_0 )} & {-c} \\ \end{array} }\right)\left({\begin{array}{*{20}c} {u_1 } \\ {\widetilde {u}_1 } \\ \end{array} }\right)=\left({\begin{array}{*{20}c} 0 \\ {H(u_0 )} \\ \end{array} }\right), $ | (18) |
其中
| $ G(u_0 )=r+2r\alpha u_0 -3r\beta u_0^2 -2r(1+\alpha -\beta )u_0, \\ H(u_0 )=r(1+\alpha -\beta )u_0 (-ru_0 -\alpha ru_0^2 +\beta ru_0^3 +r(1+\alpha -\beta )u_0^2 ). $ |
通过以上的分析, 我们可得到如下的结论.
定理1.2 对于任意给定的
证明 设
| $ \int_{-\infty }^{+\infty } (y( s ), m( s )){\rm d} s, $ |
其中
| $ \int_{-\infty }^{+\infty} \left(y( z ), \left({\begin{array}{*{20}c} 0 \\ {H(u_0 )} \\ \end{array} }\right)\right){\rm d} z=0, $ |
对所有的函数
| $ \ell ^\ast =-\frac{{\rm d}}{{\rm d}z}+\left({\begin{array}{*{20}c} 0 & {G(u_0 )} \\ {-1} & {-c} \\ \end{array} }\right). $ |
于是, 为了得到Ker
| $ \frac{{\rm d}y(z)}{{\rm d}z}=\left({\begin{array}{*{20}c} 0 & {G(u_0 )} \\ 1 & {-c} \\ \end{array} }\right)y( z ). $ |
对于系统(19)而言, 由于其系数矩阵是一个非常数矩阵, 所以很难找到其一般形式的解.然而, 我们只需要找满足
为了验证上面的理论分析和验证时滞对行波解动力学行为的影响, 借助数值方法来对系统(2)进行验证.选取1维的空间来反应该种群在空间的分布状况.在所有的数值结果中, 系统的边界条件为Neumann边界条件且空间范围为
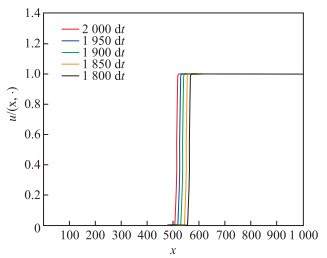
|
图 1 当取 |
从上面的数值模拟结果表明, 种群模型的时空滞后项中的时滞对该系统的行波动力学行为有着重要的影响.当时滞量非常小的时候, 系统存在单调递增的波前解.但是, 随着时滞的增加, 系统行波解的波形也随之发生变化.当时滞增加到某一数值时, 行波解开始出现振荡衰减到空间均匀状态的情况.然后当时滞继续增加到某一临界值时, 行波解又开始出现振荡尾巴的现象.这些结果的生物解释和意义为:现实生态环境中的种群在一定的情况下, 种群在空间的分布呈现出行波的传播方式, 而且种群个体因食物资源竞争所导致的相互作用时间对种群的空间传播行为有着重要的影响.当种群因食物资源竞争相互作用的时间比较少时, 种群可以获得快速的增长, 从而有利于种群在空间方向上的传播; 当种群因食物资源竞争相互作用的时间比较大时, 种群的增长受到了抑制, 从而导致种群在空间传播出现振荡的行为.另外可以借助行波的波速和振幅, 预测种群在空间传播的速度和传播的范围, 为提前做好种群资源的管理, 特别是某些有害入侵物种的控制提供一些理论方面的帮助和指导.
3 结论本文主要讨论了一类带时空滞后的单种群模型的行波解模式的存在性, 具体地讲主要做了如下方面的工作:首先利用奇异几何摄动理论讨论该种群模型在小时滞的情况下波前解的存在性; 然后借助数值计算的方法, 选取合适的系统参数, 来验证前面所得到的理论分析.以上所得到的结果说明了种群在空间分布的波动行为, 也表明了种群随着自身相互作用时间的变化其空间分布的波动行为也随之发生改变.该结果可以为生物学家分析某类入侵种群在空间分布上的传播速度和传播范围提供一定的指导和借鉴.
| [1] | WU J, ZOU X. Travelling wave fronts of reaction diffusion systems with delays[J]. Journal of Dynamics and Differential Equations, 2001, 13(3): 651-687. DOI:10.1023/A:1016690424892 |
| [2] | ZOU X. Delay induced traveling wave fronts in reaction diffusion equation of Kpp-Fisher type[J]. Journal of Computation and Applied Mathematics, 2002, 146(2): 309-321. DOI:10.1016/S0377-0427(02)00363-1 |
| [3] | WANG Z C, LI W T, RUAN S G. Traveling wave fronts in reaction-diffusion systems with spatio-temporal delays[J]. Journal of Differential Equation, 2006, 222(1): 185-232. DOI:10.1016/j.jde.2005.08.010 |
| [4] | LI W T, RUAN S G, WANG Z C. On the diffusive Nicholson's blowflies equation with nonlocal delay[J]. Journal of Nonlinear Science, 2007, 17(6): 505-525. DOI:10.1007/s00332-007-9003-9 |
| [5] | WANG Z, LI W, RUAN S. Existence and stability of traveling wave fronts in reaction advection diffusion equations with nonlocal delay[J]. Journal of Differential Equations, 2007, 238(1): 153-200. DOI:10.1016/j.jde.2007.03.025 |
| [6] | LI W T, LIN G, RUAN S G. Existence of travelling wave solution in delayed reaction diffusion systems with applications to diffusion competition systems[J]. Nonlinearity, 2006, 19(6): 1253-1273. DOI:10.1088/0951-7715/19/6/003 |
| [7] | ZHANG J M, PENG Y H. Travelling waves of the diffusive Nicholson's blowflies equation with strong generic delay kernel and non-local effect[J]. Nonlinear Analysis, 2008, 68(5): 1263-1270. DOI:10.1016/j.na.2006.12.019 |
| [8] | FENICHEL N. Geometric singular perturbation theory for ordinary differential equations[J]. Journal Differential Equations, 1979, 31(1): 53-98. DOI:10.1016/0022-0396(79)90152-9 |
| [9] | SHERRATT J A. Invading wave fronts and their oscillatory wakes are linked by a modulated travelling phase resetting wave[J]. Physica D, 1998, 117(1): 145-166. |
| [10] | BRITTON N F. Aggregation and the competitive exclusion principle[J]. Journal of theoretical biology, 1989, 136(1): 57-66. DOI:10.1016/S0022-5193(89)80189-4 |



