0 引言

随着金融市场的迅速发展, 金融市场日益呈现出高度的不确定性和高风险性.金融活动在给投资者带来高额回报的同时, 也蕴含着极大的风险.回望期权是一种强路径依赖性期权, 它在到期日的收益依赖于整个期权在有效期内风险资产的最大值或最小值, 这样使得回望期权在交割日的收益比较高, 价格非常昂贵, 更有研究的意义.

国外早期关于回望期权的定价问题由Goldman等^[1], Conze和Viswanathan^[2]以及Garman^[3]提出, 给出了经典B-S模型连续情形下欧式浮动执行价的回望期权的闭形式解. Broadie等^[4]则讨论了离散情形下的欧式浮动执行价格的欧式回望期权定价问题. Aitsahlia和Lai^[5]应用随机分析的二元性提出了一个监测欧式回望期权估计的数值方法.近年来, 许多中国学者在回望期权的研究方面也取得了很好的成绩, 袁国军等^[6]讨论了有交易成本的回望期权定价问题, 戴民运用二叉树方法讨论了回望期权的定价问题, 详细给出了路径依赖期权的数值方法.此外, 还有许多学者对回望期权的定价方法做了很深入的研究.

为了使期权的定价更加准确, 国内外许多专家学者在期权定价时引入了分数布朗运动、混合分数布朗运动, 并且考虑了交易费等情况, 其中国外的Peters^[7]首先提出了用分数布朗运动来刻画资产价格的变化.随后Rogers^[8]又对分数布朗运动下的套期保值问题进行了研究, 发现分数布朗运动路径积分理论下的市场存在着套利机会.国内的孙琳^[9]给出了分数布朗运动带交易费用的期权定价公式.桑利恒等^[10]也给出了分数布朗运动下回望期权定价公式, 王晓天等人^[11-12]利用泰勒展开方法得到了混合布朗情形下带交易成本的欧式期权定价, 并且讨论了多维分数布朗运动模型下带交易成本的Merton模型, 扩展了原有的结果.而Kabanov和Safarian^[13]计算了Leland方法中带交易费用欧式看涨期权价值的极限保值误差, Grandits和Schachingery^[14]则进一步优化了Leland方法的证明. Merton^[15]运用二项式模型构建了两阶段的期权复制策略, 导出了支付固定比例交易成本时的期权定价模型, 并考虑了保值组合债券在调整时产生的交易成本.国内学者利用证券组合技术和无套利原理建立了带交易费用的多资产期权定价模型, 利用无套利原理和对冲组合策略得到了分数布朗运动下有红利支付和存在交易费用的期权定价公式.

本文在考虑交易费的基础上, 结合混合分数布朗运动模型, 建立了混合分数布朗运动下带有交易费的回望看跌期权定价模型, 并给出了数值解.最后, 通过数值实验验证了该方法的有效性.

1 定价模型 1.1 模型假设

(ⅰ)允许卖空股票;

(ⅱ)无套利机会;

(ⅲ)投资者按无风险利率$r$贷入或贷出;

(ⅳ)令$\{ {B_t| {t\in[ {0, T}]}} \}$表示银行货币账户$B$在$t$时刻的价值, 满足以下方程

$ \begin{align} {\rm d}B_t =rB_t {\rm d}t, \quad B_0 =1; \end{align} $

(1.1)

(ⅴ)假设标的股票价格$S_t $满足随机微分方程

$ \begin{align} {\rm d}S_t =\mu S_t {\rm d}t+\sigma _1 S_t {\rm d}B_t ^H+\sigma _2 S_t {\rm d}B_t , \end{align} $

(1.2)

其中$\mu$为漂移系数, $\sigma_1$, $\sigma_2$为扩散系数, $B_t^H $为以$H$为参数的分数布朗运动, $B_t$服从标准布朗运动, ${\rm d}B=\Phi \sqrt {{\rm d}t} $, ${\rm d}B_t^H =\Phi {\rm d}t^H$, $\Phi $是服从标准正态分布的随机变量;

(ⅵ)买卖标的股票需要支付固定交易费用$\kappa |v_t|S_t $, 其中$v_t $是$t$时刻交易标的股票价格变化的份额, $v_t >0$表示买进, $v_t <0$表示卖出, $\kappa >0$为交易费固定比率;

(ⅶ)对冲投资组合的期望回报率等于无风险利率.

1.2 模型推导

定理1  考虑具有浮动执行价格的回望看跌期权, 相应的路径依赖变量$J_t =\max \limits_{0\le u\le t} S_u $, 假设标的股票价格$S_t $满足随机微分方程(1.2), 则混合分数布朗运动下带固定交易费率的回望看跌期权价值$V=V(S_t , J_t , t)$满足如下数学模型:

$ \begin{align} \left\{\!\! \begin{array}{l} \dfrac{\partial V}{\partial t}+( \widetilde{\sigma }_1 +\widetilde {\sigma }_2 )S_t^2 \dfrac{\partial ^2V}{\partial S_t ^2}+(r-q)S_t \dfrac{\partial V}{\partial S_t }-rV=0, \\ V(S_T , J_T , T)=J_T -S_T \quad ( {0\le S_T \le J_T <\infty } ), \\ {\dfrac{\partial V}{\partial J_t }} \Big|_{S_t =J_t } =0\quad ( {0\le t\le T}), \end{array} \right. \end{align} $

(1.3)

其中

$ \begin{align*} \begin{array}{l} \widetilde {\sigma }_1 =H\sigma _1^2 t^{2H-1} +\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1( {\delta t})^{H-1}, \\ \widetilde {\sigma }_2 =\dfrac{1}{2}\sigma _2^2 +\sqrt {\dfrac{2}{{\pi }\delta t}} \kappa \sigma _2, \\ \end{array} \end{align*} $

这里$\delta t$表示对冲时间间隔.

证明  考虑一个期权买方对冲的投资组合:一份回望看跌期权多头和$\Delta $份标的资产空头组成, 则该组合的价值为

$ \begin{align} \Pi =V_t -\Delta S_t , \end{align} $

(1.4)

由分数伊藤公式得

$ \begin{align} {\rm d}V=\Big( {\dfrac{\partial V}{\partial t}+H\sigma _1 ^2t^{2H-1}S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }+\dfrac{1}{2}\sigma _2^2 S_t^2 \dfrac{\partial ^2V} {\partial S_t^2 }}\Big){\rm d}t+\dfrac{\partial V}{\partial J_t }{\rm d}J_t +\dfrac{\partial V}{\partial S_t }{\rm d}S_t. \end{align} $

(1.5)

在实际情况中, 离散市场交易时间对$\Pi $加以调整, 组合在每个时间段$\delta t$内进行一次保值, 其中$\delta t$为无穷小量.而股价的变化为

$ \begin{align} \delta S_t =\mu S_t \delta t+\sigma _1 S_t \delta B_t ^H+\sigma _2 S_t \delta B_t . \end{align} $

(1.6)

将交易成本看成由于投资者买卖金融资产时的直接费用, 以交易额的固定比率$\kappa$来表示, 当期权在有效期内标的股票头寸发生$v_t$份额变化时, 交易费用为$\kappa|v_t|S_t $.如果期权在有效期内股票的头寸只发生了一次变化, 在经历$\delta t$时间段后, $\Pi$的变化为

$ \begin{align} \delta \Pi =\delta V-( {\Delta \delta S_t +\kappa| v_t| S_t } )-q\Delta S_t \delta t. \end{align} $

(1.7)

为了达到对冲的目的, 需尽量减小风险, 取$\Delta =\frac{\partial V}{\partial S_t }$.

将式(1.5)、(1.6)代入式(1.7), 得到

$ \begin{align} & \delta \Pi =\delta V-({\Delta \delta S_t +\kappa \vert v_t \vert S_t })-q\Delta S_t \delta t \notag\\ & \quad =\Big({\dfrac{\partial V}{\partial t}+H\sigma _1 ^2t^{2H-1}S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }+\dfrac{1}{2}\sigma _2^2 S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }}\Big)\delta t+ \dfrac{\partial V}{\partial J_t }\delta J_t \notag\\ &\qquad +\dfrac{\partial V}{\partial S_t }\delta S_t -\Big( {\dfrac{\partial V}{\partial S_t }\delta S_t -\kappa |v_t|S_t } \Big)-q\dfrac{\partial V}{\partial S_t }S_t \delta t \notag\\ & \quad =\Big( {\dfrac{\partial V}{\partial t}+H\sigma _1 ^2t^{2H-1}S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }+\dfrac{1}{2}\sigma _2^2 S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }} \Big)\delta t+\dfrac{\partial V}{\partial J_t }\cdot\dfrac{\partial J}{\partial t}\delta t \notag\\ &\qquad +\kappa |v_t|S_t -q\dfrac{\partial V}{\partial S_t }S_t \delta t. \end{align} $

(1.8)

保值调整策略而产生的交易变化份额$v_t$为

$ \begin{align} v_t =\dfrac{\partial V}{\partial S_t }(S+\delta S, t+\delta t)-\dfrac{\partial V}{\partial S_t }(S, t). \end{align} $

(1.9)

对式(1.9)进行泰勒展开, 得到

$ \begin{align} v_t =&\dfrac{\partial ^2V}{\partial S_t^2 }(S, t)\delta S+ \dfrac{\partial ^2V}{\partial S_t \partial t}(S, t)\delta t+\cdots \notag\\ =&(\mu S_t \delta t+\sigma _1 S_t \Phi \delta t^H+\sigma _2 S_t \Phi \sqrt {\delta t} )\dfrac{\partial ^2V}{\partial S_t^2 }+\dfrac{\partial ^2V} {\partial S_t \partial t}(S, t)\delta t+\cdots , \end{align} $

(1.10)

其中$H\in( {\frac{1}{2}, 1})$.忽略掉$\sqrt {\delta t} $的高阶无穷小量, 则有

$ \begin{align} v_t \approx (\sigma _1 S_t \Phi \sqrt {\delta t^H} + \sigma _2 S_t \Phi \sqrt {\delta t} )\dfrac{\partial ^2V}{\partial S_t^2 }. \end{align} $

(1.11)

所以在时间间隔为$\delta t$时, 期望交易费为

$ \begin{align} E(\kappa S_t|v_t|)=E\Big({\kappa \sigma _1 S_t^2 \Phi \sqrt {\delta t^H} \dfrac{\partial ^2V}{\partial S_t^2 }+\kappa \sigma _2 S_t^2 \Phi \sqrt {\delta t} \dfrac{\partial ^2V}{\partial S_t^2 }}\Big). \end{align} $

(1.12)

对$\forall t>s\ge 0$, 分数布朗运动的增量满足

$ \begin{align} &B^H(t)-B^H(s)\sim N({0, |{t-s}|^{2H}}), \\ E( {\kappa | {\nu _t }|S_t })&=\Big[ {\kappa \sigma _1 S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }\Phi( {\delta t} )^H} \Big|+\kappa \sigma _2 S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }(S_t , t)\Phi \sqrt {\delta t} \delta } \Big|} \Big] \notag\\ &=\sqrt {\dfrac{2}{\pi }} \kappa \sigma _1 ( {\delta t} )^HS_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|+\sqrt {\dfrac{2}{\pi }} \kappa \sigma _2 \sqrt {\delta t} S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|+O( {\delta t})^H \notag\\ & \approx \sqrt {\dfrac{2}{\pi }} \kappa \sigma _1( {\delta t} )^HS_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|+ \sqrt {\dfrac{2}{\pi }} \kappa \sigma _2 \sqrt {\delta t} S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|, \end{align} $

(1.13)

所以

$ \begin{align} E(\delta \Pi )=&\Big( {\dfrac{\partial V}{\partial t}+H\sigma _1 ^2t^{2H-1}S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }+\dfrac{1}{2}\sigma _2^2 S_t^2 \dfrac{\partial ^2V} {\partial S_t^2 }} \Big)\delta t+\dfrac{\partial V}{\partial J_t }\cdot \dfrac{\partial J}{\partial t}\delta t \notag\\ &-q\dfrac{\partial V}{\partial S_t }S_t \delta t+\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1 ( {\delta t})^HS_t^2\Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|+\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _2 \sqrt {\delta t} S_t^2\Big| {\dfrac{\partial ^2V}{\partial S_t^2 }}\Big|. \end{align} $

(1.14)

又由于

$ \begin{align} E(\delta \Pi )=r\Pi \delta t=r(V-\Delta S_t )\delta t=r\Big( {V-\dfrac{\partial V}{\partial S_t }S_t }\Big)\delta t, \end{align} $

(1.15)

故综合式(1.14)与式(1.15)可得

$ \begin{align} &\Big( {\dfrac{\partial V}{\partial t}+H\sigma _1 ^2t^{2H-1} S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }+\dfrac{1}{2}\sigma _2^2 S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }} \Big)+\dfrac{\partial V}{\partial J_t }\cdot \dfrac{\partial J}{\partial t}+(r-q)\dfrac{\partial V}{\partial S_t }S_t \notag\\ +&\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1 ( {\delta t} )^{H-1}S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|+\sqrt {\dfrac{2}{{\pi }\delta t}} \kappa \sigma _2 S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|=r. \end{align} $

(1.16)

由于路径依赖变量$J_t =\max \limits_{0\le u\le t} S_u $对$t$显然是不可微的, 故先对它进行逼近.定义

$ \begin{align} J_n (t)=\Big[ \frac{1}{t}\int\nolimits_0^t {({S_\tau })^n{\rm d}\tau } \Big]^{\frac{1}{n}}, \end{align} $

(1.17)

则$J_n (t)$对$t$是可微的.

因为$S_t $对$t$是连续函数, 从而当$n\to \infty $时,

$ \begin{align} \lim\limits_{n\to \infty } J_n (t)=\max\limits_{0\le \tau \le t} S_\tau =J_t . \end{align} $

(1.18)

则以$J_n (t)$来近似代替$J_t $, 有

$ \begin{align} \delta J_n (t)=\dfrac{( {\frac{S_t }{J_n ( t)}} )^{n-1}S_t -J_n ( t )}{nt}\delta t, \end{align} $

(1.19)

故当$n\to \infty $时, $\delta J_t \to 0$.从而有

$ \begin{align} &\Big( {\dfrac{\partial V}{\partial t}+H\sigma _1 ^2t^{2H-1}S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }+\dfrac{1}{2}\sigma _2^2 S_t^2 \dfrac{\partial ^2V}{\partial S_t^2 }} \Big)+(r-q)\dfrac{\partial V}{\partial S_t }S_t \notag\\ +& \sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1 ( {\delta t} )^{H-1}S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }} \Big|+\sqrt {\dfrac{2}{{\pi }\delta t}} \kappa \sigma _2 S_t^2 \Big| {\dfrac{\partial ^2V}{\partial S_t^2 }}\Big|=rV\, (0\le S\le J< \infty , 0\le t\le T). \end{align} $

(1.20)

上式中$\frac{\partial V}{\partial S_t }$是保值的因子, 而$\frac{\partial ^2V}{\partial S_t^2 }$是交易的频率.由文献分析可知, $\frac{\partial ^2V}{\partial S_t^2 }$恒为正值才有意义, 因此, 带有交易费用的回望看跌期权的定价模型为

$ \begin{align} \dfrac{\partial V}{\partial t}+&\Big\{ H\sigma _1^2 t^ {2H-1} +\dfrac{1}{2}\sigma _2^2 +\sqrt {\dfrac{2}{\pi }} \kappa \sigma _1 ( {\delta t} )^{H-1}+\sqrt {\dfrac{2}{\pi \delta t}} \kappa \sigma _2 \Big\}S_t^2 \dfrac{\partial ^2V}{\partial S_t ^2}\notag\\ +&(r-q)S_t \dfrac{\partial V}{\partial S_t }-rV=0 (0\le S\le J< \infty , 0\le t\le T). \end{align} $

(1.21)

不妨令

$ \begin{align*} \begin{array}{l} \widetilde {\sigma }_1 =H\sigma _1^2 t^{2H-1} +\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1 ( {\delta t} )^{H-1}, \\ \widetilde {\sigma }_2 =\dfrac{1}{2}\sigma _2^2 +\sqrt {\dfrac{2}{{\pi }\delta t}} \kappa \sigma _2 , \end{array} \end{align*} $

则式(1.21)可化简为

$ \begin{align} \dfrac{\partial V}{\partial t}+( {\widetilde {\sigma }_1 +\widetilde {\sigma }_2 } )S_t^2 \dfrac{\partial ^2V}{\partial S_t ^2}+ (r-q)S_t \dfrac{\partial V}{\partial S_t }-rV=0, \end{align} $

(1.22)

终边条件为

$ \begin{align*} V(S_T , J_T , T)=J_T -S_T \quad ( {0\le S_T \le J_T <\infty }), \end{align*} $

边界条件为

$ \begin{align*} {\dfrac{\partial V}{\partial J_t }} \Big|_{S_t =J_t } =0\quad ( {0\le t\le T}). \end{align*} $

综上可证

$ \begin{align*} \left\{\!\! {\begin{array}{l} \dfrac{\partial V}{\partial t}+({\widetilde {\sigma }_1 + \widetilde {\sigma }_2 })S_t^2 \dfrac{\partial ^2V}{\partial S_t ^2}+(r-q)S_t \dfrac{\partial V}{\partial S_t }-rV=0, \\ V(S_T , J_T , T)=J_T -S_T \quad ( {0\le S_T \le J_T <\infty }), \\ {\dfrac{\partial V}{\partial J_t }}\Big|_{S_t =J_t } =0\quad ( {0\le t\le T}), \end{array}} \right. \end{align*} $

其中

$ \begin{align*} \begin{array}{l} \widetilde {\sigma }_1 =H\sigma _1^2 t^{2H-1} +\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1 ( {\delta t} )^{H-1}, \\ \widetilde {\sigma }_2 =\dfrac{1}{2}\sigma _2^2 +\sqrt {\dfrac{2}{{\pi }\delta t}} \kappa \sigma _2 . \end{array} \end{align*} $

由于模型(1.22)中的$\widetilde {\sigma }_1 $、$\widetilde {\sigma }_2 $是非线性的, 我们不易求出模型中偏微分方程的解析解, 故为便于讨论, 在下节中构造Crank-Nicolson数值格式来讨论其数值解的情况.

2 模型求解

由于在上一节中建立的模型是一个4维问题, 不便于求解, 故先将其转化成3维问题.作如下变量替换

$ \begin{align*} x=\ln \dfrac{J_t }{S_t }, \quad V(S_t , J_t , t)=S_t u( {x, \tau } ), \quad \tau =T-t, \end{align*} $

则有

$ \begin{align*} \dfrac{\partial V}{\partial t}=-S_t \dfrac{\partial u} {\partial \tau }, \quad \dfrac{\partial V}{\partial S_t }=u-\dfrac{\partial u}{\partial x}, \quad \dfrac{\partial ^2V}{\partial S_t^2 }=\dfrac{1}{S_t }\Big[ {\dfrac{\partial ^2u}{\partial x^2}-\dfrac{\partial u}{\partial x}} \Big]. \end{align*} $

故式(1.22)变为

$ \begin{align} -S_t \dfrac{\partial u}{\partial \tau }+( {\widetilde {\sigma } _1 +\widetilde {\sigma }_2 } )S_t \Big[ {\dfrac{\partial ^2u}{\partial x^2}-\dfrac{\partial u}{\partial x}}\Big]+(r-q)S_t\Big ( {u-\dfrac{\partial u}{\partial x}} \Big)-ruS_t =0. \end{align} $

(2.1)

模型(1.3)变形为

$ \begin{align} \left\{\!\! {\begin{array}{l} \dfrac{\partial u}{\partial \tau }+( {\widetilde {\sigma }_1 +\widetilde {\sigma }_2 +r-q} )\dfrac{\partial u}{\partial x}-(\widetilde {\sigma }_1 +\widetilde {\sigma }_2 )\dfrac{\partial ^2u}{\partial x^2}+qu=0, \\ u(x, \tau )| {_{\tau =0} ={\rm e}^x-1 ( {0<x<\infty }), } \\ \dfrac{\partial u}{\partial x}\Big|_{{x=0}} =0\quad ( {0\le \tau \le T}), \\ \end{array}} \right. \end{align} $

(2.2)

其中

$ \begin{align} \begin{array}{l} \widetilde {\sigma }_1 =H\sigma _1^2 (T-\tau )^{2H-1} +\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1 ( {\delta t} )^{H-1}, \\ \widetilde {\sigma }_2 =\dfrac{1}{2}\sigma _2^2 +\sqrt {\dfrac{2}{{\pi }\delta t}} \kappa \sigma _2 . \end{array} \end{align} $

(2.3)

接下来利用Crank-Nicolson格式将式(2.2)中的非线性问题进行离散化处理.首先对截断区域$\Omega=[ {0, x_{\max } } ] \times [ {0, T} ]$进行如下等距分割.

将期权的期限$T$分成$N$个等间隔, 长度为$l=T/N$的时间区间, 因此需考虑以下$N+1$个时间点

$ \begin{align*} 0, l, \cdots , T. \end{align*} $

给定正整数$M$, 定义空间步长$h=x_{\max } /M $, 我们需同时考虑以下$M+1$个空间点

$ \begin{align*} 0, h, \cdots , x_{\max } . \end{align*} $

构造一组离散点$(x, \tau )=(x_k , \tau _n )$, 这里$x_k =kh\, ( {k=0, 1, 2, \cdots , M})$, $\tau _n =nl\, (n=0, 1, 2, \cdots , N)$, 设$u(x_k , \tau _n )$的近似值为$u_k^n $, 对时间偏导数和空间偏导数分别作如下差分近似

$ \begin{align*} \dfrac{\partial u}{\partial \tau }( {x_k , \tau _n }) &\approx \dfrac{u_k^{n+1} -u_k^n }{l}, \dfrac{\partial u}{\partial x}(x_k , \tau _n )\approx \dfrac{1}{2}\Big( {\dfrac{u_{k+1}^n -u_{k-1}^n }{2h}+\dfrac{u_{k+1}^{n+1} -u_{k-1}^{n+1} }{2h}} \Big), \\ \dfrac{\partial ^2u}{\partial x^2}(x_k , \tau _n )&\approx \dfrac{1}{2}\Big( {\dfrac{u_{k+1}^n -2u_k^n +u_{k-1}^n }{h^2}+\dfrac{u_{k+1}^{n+1} -2u_k^{n+1} +u_{k-1}^{n+1} }{h^2}} \Big). \end{align*} $

将以上近似值代入模型(2.1)中, 则可以得到标准Crank-Nicolson数值格式

$ \begin{align} \left\{\!\!\begin{array}{l} \dfrac{u_k^{n+1} -u_k^n }{l}+\dfrac{1}{2}( {\widetilde {\sigma }_1 +\widetilde {\sigma }_2 +r-q} )\Big( {\dfrac{u_{k+1}^n -u_{k-1}^n }{2h}+\dfrac{u_{k+1}^{n+1} -u_{k-1}^{n+1} }{2h}} \Big) \\ -\dfrac{1}{2}(\widetilde {\sigma }_1 +\widetilde {\sigma }_2 )\Big( {\dfrac{u_{k+1}^n -2u_k^n +u_{k-1}^n }{h^2}+\dfrac{u_{k+1}^{n+1} -2u_k^{n+1} +u_{k-1}^{n+1} }{h^2}} \Big)+qu_k^n =0, \\ m=\widetilde {\sigma }_1 +\widetilde {\sigma }_2 +r-q, \quad n= (\widetilde {\sigma }_1 +\widetilde {\sigma }_2 ), \end{array}\right. \end{align} $

(2.4)

其中

$ \begin{align*} \begin{array}{l} \widetilde {\sigma }_1 =H\sigma _1^2 (T-\tau _n )^{2H-1} +\sqrt {\dfrac{2}{{\pi }}} \kappa \sigma _1 ( {\delta t} )^{H-1}, \\ \widetilde {\sigma }_2 =\dfrac{1}{2}\sigma _2^2 +\sqrt {\dfrac{2}{{\pi }\delta t}} \kappa \sigma _2. \end{array} \end{align*} $

则数值格式(2.4)等价于

$ \begin{align} a_k^n u_{k+1}^{n+1} +b_k^n u_{k}^{n+1} +c_k^n u_{k-1}^{n+1} = \alpha _k^n u_{k+1}^n +\beta _k^n u_k^n +\gamma _k^n u_{k-1}^n, \end{align} $

(2.5)

其中

$ \begin{align*} \begin{array}{c} a_k^n =\dfrac{n}{2h^2}-\dfrac{lm}{4h}, \quad b_k^n =-\Big( {1+\dfrac{n}{h^2}}\Big), \quad c_k^n =\dfrac{n}{2h^2}+\dfrac{lm}{4h}, \\[2mm] \alpha _k^n =\dfrac{lm}{4h}-\dfrac{n}{2h^2}, \quad \beta _k^n =\dfrac{n}{h^2}-1+lq, \quad \gamma _k^n =\dfrac{n}{2h^2}+\dfrac{lm}{4h}, \\[2mm] m=\widetilde {\sigma }_1 +\widetilde {\sigma }_2 +r-q, \quad n=(\widetilde {\sigma }_1 +\widetilde {\sigma }_2 ), \quad 1\le k\le M-1, \quad 1\le n\le N-1. \end{array} \end{align*} $

式(2.5)就是标准的Crank-Nicolson数值格式, 为了方便数值的计算, 我们在这里定义向量

$ \begin{align*} u^n=( {u_1 ^n, u_2^n, \cdots , u_{M-1} ^n})^{\rm T}, \end{align*} $

则数值格式(2.5)可写成矩阵形式:

$ \begin{align} A(n)u^{n+1}=B(n)u^n+p^n, \end{align} $

(2.6)

其中$A(n), B(n)$是如下$(M-1)\times (M-1)$阶的矩阵

$ \begin{align*} A(n)=\left[\!\! {{\begin{array}{cccccc} {b_1^n } &{a_1^n }&0&0&\cdots&0 \\ {c_2^n }&{b_2^n }&{a_2^n }&0&\cdots &0 \\ 0&{c_3^n }&{b_3^n }&{a_3^n }&\cdots &0 \\ && \ddots&\ddots&\ddots&\\ 0&0&\cdots&{c_{M-2}^n }&{b_{M-2}^n } &{a_{M-2}^n } \\ 0&0&\cdots&0&{c_{M-1}^n } & {b_{M-1}^n } \\ \end{array} }} \!\!\right], \end{align*} $

$ \begin{align*} B(n)=\left[\!\! {{\begin{array}{cccccc} {\beta _1^n }&{\alpha _1^n }&0&0&\cdots &0 \\ {\gamma _2^n }&{\beta _2^n }&{\alpha _2^n }&0 &\cdots&0 \\ 0&{\gamma _3^n }&{\beta _3^n }&{\alpha _3^n } &\cdots&0 \\ && \ddots&\ddots&\ddots&\\ 0&0&\cdots&{\gamma _{M-2}^n }&{\beta _{M-2}^n }&{\alpha _{M-2}^n } \\ 0&0&\cdots&0&{\gamma _{M-1}^n } & {\beta _{M-1}^n } \\ \end{array} }} \!\!\right], \end{align*} $

且$p^n$是如下形式的向量

$ \begin{align*} p^n=( {\gamma _1^n u_0^n -c_1^n u_0^{n+1} , }\quad {0, }\quad \cdots \quad {0, } \quad {\alpha _{M-1}^n u_M^n -a_{M-1}^n u_M^{n+1} } )^{\rm T}. \end{align*} $

求解数值格式(2.4)还需知道边界点$u_M^n $和$u_0^n $的值, 利用2阶Gear公式对边界条件作如下形式的离散

$ \begin{align*} {\dfrac{\partial u}{\partial x}} \Big|_{x=0} = \dfrac{3u_0^n -4u_1^n +u_2^n }{2h}=0, \end{align*} $

即

$ \begin{align} u_0^n =\dfrac{4u_1^n -u_2^n }{3}. \end{align} $

(2.7)

此外, 当标的股票价格$S_t $趋于零时, 回望看跌期权必定会被执行, 有边界条件

$ \begin{align} V( {0, J_t , t} )={\rm e}^{-r({T-t})}J_t . \end{align} $

(2.8)

进一步变量替换, 则式(2.8)可变为

$ \begin{align} u_M^n ={\rm e}^{-r\tau }. \end{align} $

(2.9)

将边界条件(2.7)和(2.9)代入数值格式(2.5), 则可利用追赶法对该格式进行求解, 且初始时刻回望看跌期权的价值$V$由$S_t u_0^N $给出.可以看出, 经过变量变换后构建的新数值格式中不含变量$J_t $, 这就避免了在数值迭代过程中$J_t $取值不确定的困难.

3 数值实验

例  考虑一只欧式回望看跌期权, 其标的资产为股票, 且股票价格$S_t $服从混合分数布朗运动, 相应的欧式回望看跌期权价值满足定理1, 即各参数取值如下.

(1) ${r}=0.5$, $\sigma_1=0.15$, $\sigma_2=0.20$, $\kappa=0.003$, ${N}=500$, ${M}=500$, ${q}=0.05$, ${T}=0.5$, ${S_t}=50$

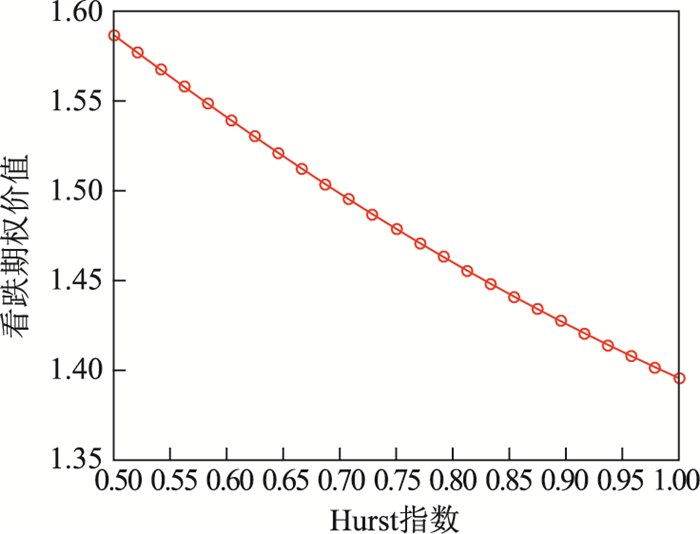
求回望看跌期权价值随Hurst指数变化图.

图 1描述了回望看跌期权价值随Hurst($H>0.5$)指数的变化情况.从图形中可以看出, 随着Hurst指数的增大, 回望看跌期权的价值在减小, 这说明了在此种条件下, 期权价值与Hurst指数呈现负相关.

(2) $r=0.5$, $\sigma_1=0.15$, $\sigma_2=0.20$, $\kappa=0.003$, $M=500$, $q=0.05$, $T=0.5$, $H=0.8$, $S_t=50$

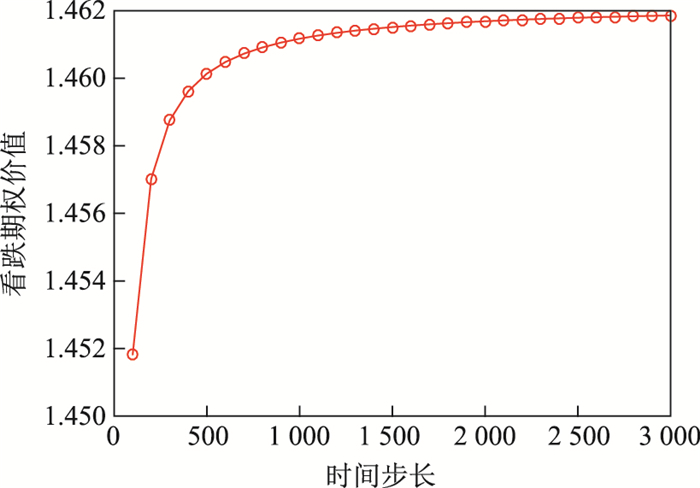
求不同时间步长下回望期权的价值收敛图.

图 2描述了回望看跌期权价值随时间步长的变化情况.从图形中可以看出, 其他参数不变, 随着时间步长的增大, 回望看跌期权的价值逐渐收敛到一个数值, 同时说明数值格式的有效性.

(3) $r=0.5$, $\sigma_1=0.15$, $\sigma_2=0.20$, $\kappa=0.005$, $N=300$, $M=300$, $q=0.15$, $H=0.6$

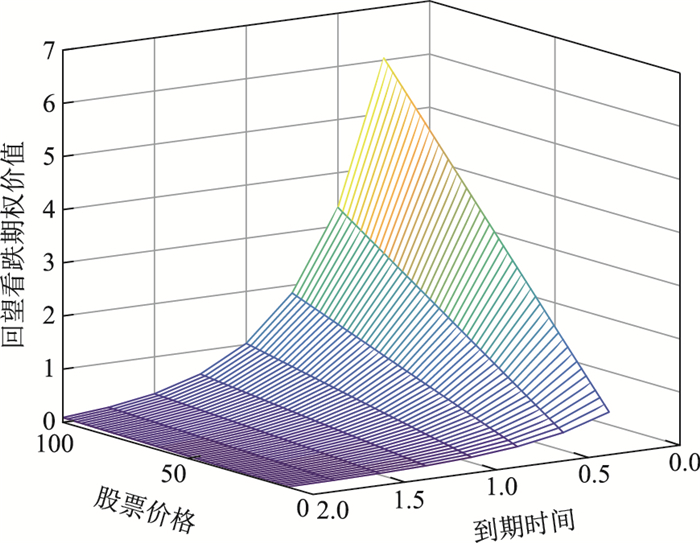
求回望看跌期权价值随到期时间和股票价格变化时的3维立体图.

图 3描述了回望看跌期权价值随到期时间和股票价格的变化情况.从图形中可以看出, 其他参数不变, 随着到期日的增大, 期权的价值也随之增大; 随着股票价格增大, 相应回望看跌期权价值也在增大.这主要是由于回望看跌期权的执行价格是浮动的, 并且随着标的资产价格的增大而增大, 因此期权的价值也会增大.

(4) $r=0.5$, $H=0.6$, $T=1$, $\kappa=0.005$, $N=300$, $M=300$, $q=0.15$, $S_t=80$

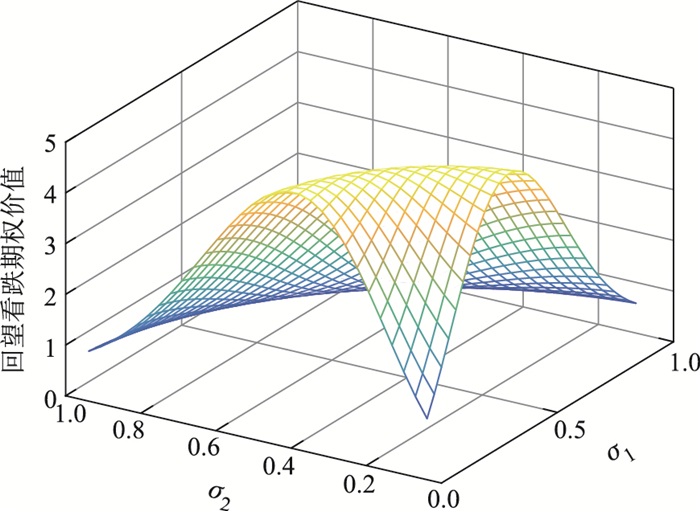
求回望看跌期权价值随两个波动率的变化图.

图 4描述了回望看跌期权价值随两个波动率变化情况.从图形中可以看出, 回望看跌期权的价值随两个波动率的变化情况呈现抛物线状.这是由于文中回望期权定价公式中涉及到两个波动率的平方的原因.

(5) $T=0.5$, $r=0.5$, $\sigma_1=0.15$, $H=0.5$, $N=400$, $M=300$, $\sigma_2=0.20$, $q=0.15$

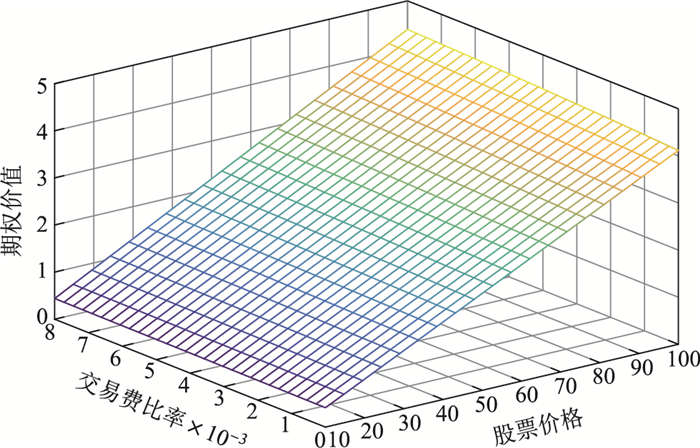
求回望看跌期权价值随交易费比率和股票价格变化的3维立体图.

图 5描述了回望看跌期权价值随交易费比率和股票价格的变化情况.从图形中可以看出, 其他参数不变, 随着交易费比率的减小, 股票价格的增加, 相应回望看跌期权的价值也在增大.这主要是由于回望看跌期权的执行价格是浮动的, 并且随着标的资产价格的增大而增大, 因此期权的价值也会增大.

4 结论

本文对在混合分数布朗运动模型下带有固定交易费用的欧式回望看跌期权进行定价时, 首先采用对冲方法建立回望期权价值所满足的数学模型; 然后构造了一种Crank-Nicolson格式求得它的数值解; 最后利用Matlab软件对该格式进行数值实验, 并讨论了各个参数对期权价值的影响.