随着计算技术日益提升, 全球教育信息化蓬勃发展.尤其是在线教育市场呈现出爆发式增长.题目测试一直是教育和学习的重要组成部分.在题目测试中, 题库一直处于在线教育的中心位置.借助于大数据存储、计算和分析等技术, 题库的规模日益扩大, 但也暴露出一些问题, 题目的质量良莠不齐, 重复或高度相似题目日益增多, 给教育行业的使用带来很大的困扰.因此, 为了保证题库及教学质量, 快速找出这些重复或高度相似题目就显得十分重要.
题目的主要表现形式是文本.现有的计算字符串相似度的方法按照计算所需的特征的不同, 可以划分为3种方法:基于字面相似的方法、基于统计关联的方法、基于语义相似的方法, 以及综合这3种方法的多层特征方法[1-3].题目与普通短文本的主要区别在于, 题目表述的内容更趋向于字面化, 且文本长度较长.因此本文采用基于字面相似的计算方法来判断两个题目的相似度.基于字面相似的计算方法主要有基于编辑距离的计算方法[4]和基于相同字或词的方法[5].其中, 编辑距离法应用广泛, 计算方法相对成熟.本文将一个题目看作为一个字符串, 通过计算2个字符串的编辑距离来判断2个题目彼此是否相似[6].文献[7]通过修改操作代价, 提高了算法的精准度, 文献[8]通过扩展交换操作, 提高了算法的精确度, 虽然文献[7]和文献[8]都提高了算法的精准度, 但同时也都增加了计算量.
本文分析Levenshtein距离矩阵中元素的内在关系, 提出一种提前终止的优化策略, 可预判编辑距离是否满足预设阈值, 并将该优化策略用于大规模题目匹配.本文的主要贡献在于提出并证明了定理1, 并根据定理1提出了提前终止的计算优化策略.该策略不仅可以提前判断两字符串是否不相似, 还可以提前判断两字符串是否相似, 并且实现了并行程序加速匹配过程.经过大量的实验, 测试结果表明:根据该优化算法得出的结果与原算法得出的结果相同, 且显著减少计算时间.
本文组织结构如下:第1节先介绍原Levenshtein算法的相关内容; 第2节提出对原Levenshtein算法的优化, 和优化策略的理论证明, 以及对应的时间复杂度的分析; 第3节介绍在实验过程中使用的两种优化策略, 以及对比优化前和优化后的编辑算法在处理相同数据集下的效率.第4节是总结.
1 Levenshtein算法简介 1.1 Levenshtein距离基本思想Levenshtein距离又称编辑距离, 由俄国科学家Vladimir Levenshtein于1965年提出[9], 指从源字符串
设有2个字符串
| $ \begin{align} d_{i, j}= \left\{ \begin{array}{l}i, \quad j=0, \\ j, \quad i=0, \\ \min\left\{ \begin{array}{l}d_{i-1, j-1}+a_{i, j}, \\ d_{i, j-1}+1, \quad \quad \quad i>0, j>0, \\ d_{i-1, j}+1, \\ \end{array} \right.\\ \end{array} \right. \end{align} $ | (1) |
其中
| $ \begin{align*} a_{i, j}=\left\{ \begin{array}{l}0\quad s_i=t_j\\ 1\quad s_i\neq t_j \end{array} \right. (i=1, 2, \cdots, m;j=1, 2, \cdots, n). \end{align*} $ |
矩阵
根据编辑距离
| $ Sim=1-\frac{ld}{\max(n, m)} . $ | (2) |
式(2)中
以
|
表 1 字符串 |
从表 1可知,
根据第1.2节可知,
因此,
|
表 2 |
根据表 1可知,
| $ \forall i, 0\leq i<m, d_{m, n}\geq d_{m-i, n-i}. $ |
根据如上的观察, 提出如下定理.
定理1
证明 设
| $ d_{i, j}=X;d_{i+1, j+1}=Y;d_{i+1, j}=Z.\\ S_1=s_1 s_2\cdots s_i; T_1=t_1 t_2\cdots t_j; S_2=s_1\cdots s_i s_{i+1}=S_1 s_{i+1}; T_2=t_1\cdots t_j t_{j+1}=T_1 t_{j+1}. $ |
根据式(1)可知,
① 若
根据式(1)中的
② 若
因为
| $ \exists k, {0<k\leq i+1}, 使得S_k=s_k\cdots s_i s_{i+1}为 T_1 的子串; $ | (3) |
反之不一定成立.
若使用反证法证明这种情况:若不存在
需要指出的是, 若结论(3)能够成立,
若想
| $ s_{i+1}是 S_1 转换成 T_1 所需的编辑操作之一. $ | (4) |
例如在表 1中,
当
因此, 只有当新插入的
又根据式(1)可知, 若
③ 若
结合以上3种可能, 证明定理1是成立的.证毕.
令
| $ d_{m, n}\geq d_{m-1, n-1}\geq \cdots \geq d_{1, n-m+1}. $ | (5) |
根据式(5)递推关系式可以对应得到下表 3.
|
表 3 递推关系式对应 |
根据表 3, 可总结出如下结论,
| $ \forall i, {0\leq i<m}, d_{m, n}\geq d_{m-i, n-i} 恒成立. $ | (6) |
因此, 在计算Levenshtein距离的过程中,
在题目匹配中, 判定两个字符串是否相似, 需要对两个字符串的相似度设定一个阈值
| $ 1-\frac {ld}{\max(n, m)} \geq Sim. $ | (7) |
简化式(7)可得如下,
| $ n(1-Sim)\geq ld=d_{m, n.} $ | (8) |
综合式(6)和式(8), 得出如下,
| $ \exists i, {0\leq i<m}, 使得 d_{m-i, n-i}>n(1-Sim), 则 d_{m, n}>n(1-Sim) 恒成立. $ | (9) |
根据式(9)可知, 计算Levenshtein编辑距离时, 如
| $ 同理, \exists i, {0\leq i<m}, 使得d_{m-i, n-i}\leq n(1-Sim)-(m-i), 则d_{m, n}\leq n(1-Sim)恒成立. $ | (10) |
根据式(10)可知, 如
因此, 改进后的Levenshtein算法步骤如下, 改进编辑距离算法计算编辑距离流程图见图 1.
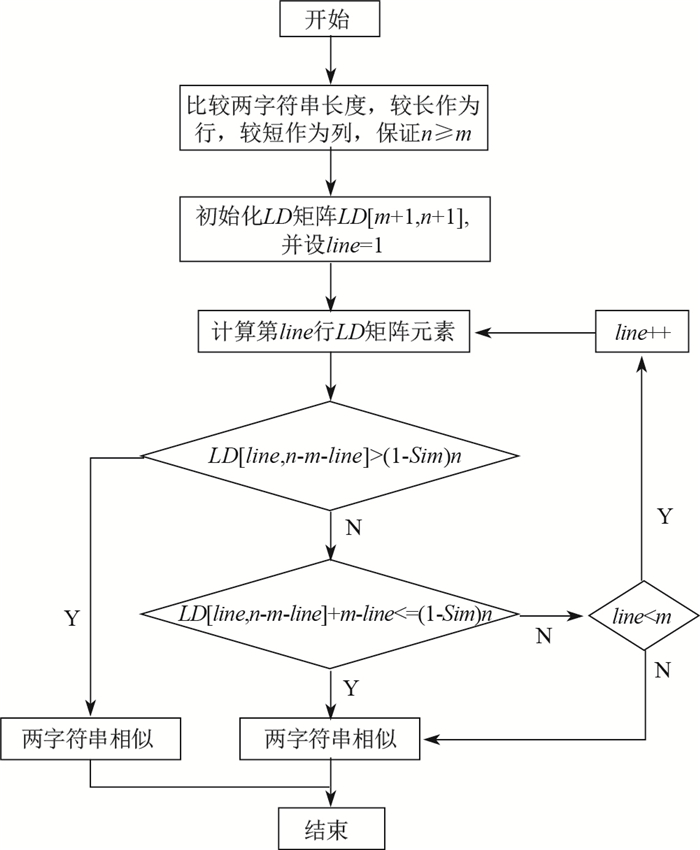
|
图 1 改进编辑距离的重复度计算过程 Fig.1 The flow of repeatability calculation for improved editing distance |
以表 1所示的
将
由结论(9)可知, 只需关注表 1矩阵中
由式(8)得出
由于该改进算法并不修改原矩阵中的数值, 而是在计算过程中根据预设的阈值进行重复度提前判定, 减少不必要的计算过程.因此改进算法匹配出的重复记录与原算法匹配出的结果是相同的, 因此该改进算法的准确性得到保证.
在文献[13]中, 提前终止思想已经使用在了两个大字符串集合中找到了相似的字符串中.在文献[13]中, 设
优化前算法的时间复杂度为
由于原算法本质上是一个矩阵计算, 本身就能够终止, 本文基于原算法提出了一种提前终止的策略, 所以该改进算法也具有终止性.
根据第2.1节的证明, 可保证该改进算法的正确性.
3 实验优化与结果分析 3.1 实验优化在实验过程中增加了两个优化过程, 一个是根据题目长度来决定两个题目是否进行匹配, 还有一个是将进行匹配的题目按照字符出现的频率由低到高重新排列.
在实验过程中发现, 若两个题目相似, 其字符串长度也很相近.如:
根据上述特点, 设定常数
| $ (1-\varepsilon)\leq \frac {S的长度}{T的长度}\leq(1+\varepsilon) . $ | (11) |
实验中, 假设
| $ d_{m, n}>d_{m-1, n-1}>\cdots>d_{1, n-m+1}. $ | (12) |
这样就能在最少的计算内满足结论(9), 可以最大幅度的提升计算效率.但当
|
表 4 字符串 |
由结论(10)可知, 关注
在进行匹配前, 先将字符串
在新的字符串
将上述的字符串
|
表 5 字符串 |
根据重新排完序之后的字符串
为了验证本文改进算法的有效性, 选取一系列真实的K12题目进行测试.实验所用的计算机配置CPU: i7-7700 8核16线程3.6 GHz、内存: 16 G.判重程序中开启16个线程进行并行匹配计算.所有学科题目的重复度阈值设置为80%.首先, 选取了10万生物试题进行详细匹配, 匹配时根据题目长度进行, 长度差别过大的试题, 默认两个题目不相似, 所以记录了相应题目长度范围内的题目个数、算法改进前后的计算量以及计算时间, 并给出相应的计算量节省百分比和计算时间节省百分比.结果详见表 6.
| 表 6 10万生物试题的各项数据指标表(80%重复度阈值) Tab.6 Calculation statistics for 100 000 biology questions (repeatablity: 80%) |
根据表 6, 将计算量节省百分比和计算时间节省百分比绘制折线图, 结果详见图 2.
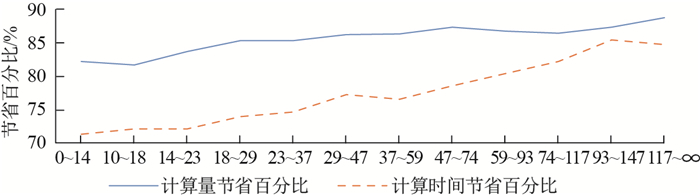
|
图 2 10万生物试题计算量和计算时间节省对比图(80%重复度阈值) Fig.2 Performance comparison of repeatability caculation saved for 100 000 biology questions (repeatability: 80%) |
从图 2中, 发现计算量节省百分比是比较稳定的, 而计算时间节省百分比却有着上升的趋势.
出现这种趋势主要是因为在题目长度较短时, 每行计算量较小, 程序运行时间较短, 因此在程序运行中的题目分配、函数调用等程序执行过程导致的延迟不能忽略不计.因而才导致了题目长度在较短时, 节约耗时的百分比与实际减少的计算量差距较大.在折线图中也可以清楚地看出随着题目长度的增长, 节约计算量百分比与节约耗时百分比的差距在不断缩小, 由于程序执行过程而导致的延迟所占比例越小.
接着选取了生物的10万、20万、30万、40万和50万不同数量的试题进行匹配, 记录了改进前后的计算时间, 以及计算时间节省百分比, 结果详见表 7.
| 表 7 不同生物试题数量实验对比表(80%重复度阈值) Tab.7 Performance comparison of repeatability calculation for biology questions in different sizes (repeatability: 80%) |
根据表 7的计算时间节省百分比, 绘制折线图, 结果详见图 3.
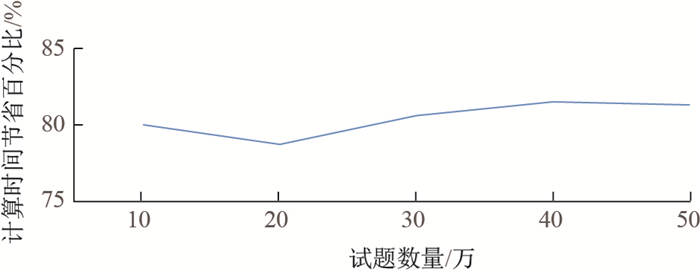
|
图 3 不同生物试题数量计算时间节省对比图(80%重复度阈值) Fig.3 Comparison of calculation time saved for biology questions in different sizes (repeatability: 80%) |
从图 3中发现在各数据量中, 计算时间节省百分比时区域稳定的, 在80%上下浮动.
最后选取语文、数学、物理、化学、地理、生物、历史和政治各50万数量的题目进行匹配, 记录了改进前后的计算时间, 以及计算时间节省百分比, 结果详见表 8.
| 表 8 不同学科实验对比表(80%重复度阈值) Tab.8 Performance comparison of repeatability calculation for multiple disciplines |
根据表 8的计算时间节省百分比, 绘制折线图, 结果详见图 4.

|
图 4 不同学科计算时间节省对比图 Fig.4 Comparison of calculation time saved for different disciplines |
分析以上结果发现, 使用改进编辑距离算法的平均计算时间节省百分比在80%左右.且两个算法所匹配出的相似题目在数量和匹配上完全相同.
由于各个学科的试题内容和知识点的不同, 所以各学科在匹配时间上各有不同, 比如在语文试题中长文本的个数居多, 所以匹配时间也是最长, 但各学科的平均计算时间节省百分比是比较稳定的, 所以本文提出的提前中止策略的效率是稳定的.
4 结论本文分析了经典Levenshtein算法生成的矩阵中内在的联系, 提出一种提前终止策略的改进算法.该改进算法不仅不影响原算法的准确性, 而且能更快速地判断出两个题目是否相似.实验结果表明, 本文提出的改进算法, 能够显著减少计算时间, 适用于大规模题库重复判定.
致谢: 感谢精锐教育(www.onesmart.org)提供的各学科试题库.| [1] | HALL P, DOWLING G. Approximate string matching[J]. ACM Computing Survey, 1980, 12(4): 381-402. DOI:10.1145/356827.356830 |
| [2] | WAGNER R, FISCHER M. The string-to-string correction problem[J]. Journal of the ACM, 1974, 21(1): 168-173. DOI:10.1145/321796.321811 |
| [3] | 章成志. 基于多层特征的字符串相似度计算模型[J]. 情报学报, 2005, 24(6): 696-701. DOI:10.3969/j.issn.1000-0135.2005.06.010 |
| [4] | MONGE A, ELKAN C. The field matching problem: Algorithms and applications[C]//Proc of ACM International Conference on Knowledge Discovery and Data Mining. New York: ACM, 1996: 267-270. |
| [5] | NIRENBURG S, DOMASHNEV C, GRANNES D. Two approaches to matching in example-based machine translation[C]//Proc of the 5th International Conference on Theoretical and Methodological Issues in Machine Translation. Kyoto: TMI, 1993: 47-57. |
| [6] | JIN L, LI C, MEHROTRA S. Efficient record linkage in large data sets[C]//Proc of the 8th International Conference on Database System for Advanced Application. Kyoto: DASFAA, 2003: 137-146. |
| [7] | 邵清, 叶琨. 基于编辑距离和相似度改进的汉字字符串匹配[J]. 电子科技, 2016, 29(9): 7-11. DOI:10.3969/j.issn.1009-6108.2016.09.004 |
| [8] | 廖宏建, 杨玉宝, 唐连章. 改进的编辑距离计算及其在自动评分中的应用[J]. 广州大学学报(自然科学版), 2012, 11(4): 79-83. DOI:10.3969/j.issn.1671-4229.2012.04.015 |
| [9] | LEVENSHTEIN V. Binary codes capable of correcting deletions, insertions and reversals[J]. Soviet Physics Doklady, 1966, 10(1): 845-848. |
| [10] | 玛依热·依布拉音, 米吉提·阿不里米提, 艾斯卡尔·艾木都拉. 基于最小编辑距离的维语词语检错与纠错研究[J]. 中文信息学报, 2008, 22(3): 110-114. DOI:10.3969/j.issn.1003-0077.2008.03.015 |
| [11] | 姜华, 韩安琪, 王美佳, 等. 基于改进编辑距离的字符串相似度求解算法[J]. 计算机工程, 2014, 40(1): 222-227. |
| [12] | 何锋, 谷锁林, 陈彦辉. 基于编辑距离相似度的文本校验技术研究与应用[J]. 飞行器测控学报, 2015, 34(4): 389-394. |
| [13] | LI G, DENG D, WANG J, et al. Pass-join:A partition-based method for similarity joins[J]. Proceedings of the VLDB Endowment, 2011, 5(3): 253-264. DOI:10.14778/2078331 |




