艾滋病(AIDS)是一类严重威胁人类健康和生命的传染病, 目前已成为全球重要的公共健康问题.艾滋病病毒(Human Immunodeficiency Virus, 简称HIV)主要感染人体免疫系统细胞CD4+T, 可引起细胞CD4+T计数的大幅度下降, 导致人体免疫缺陷, 严重影响患者防御机会性感染的能力[1]. HIV分为两种类型: HIV-1型和HIV-2型, 其屮HIV-1是引发艾滋病的主要病原体.国内外已有很多医学和数学等各方面的工作者投入到艾滋病的防治研究中, 其中借助数学模型来分析艾滋病病毒感染的动力学行为已成为一个热点研究问题[2].对于HIV-1感染的研究, Perelson、Anderson等提出了最初的模型[3-6]:
| $ \begin{align} \left\{ {{\begin{array}{*{20}c} {\dot {x}(t) = \lambda -dx(t)-\beta x(t)v(t), } \hfill \\ {\dot {y}(t) = \beta x(t)v(t)-ay(t), \quad \;} \hfill \\ {\dot {v}(t) = ky(t)-uv(t).\quad \quad \quad \;} \hfill \\ \end{array} }} \right. \end{align} $ | (1) |
其中:
在模型(1)中, 发生率被假设为:
| $\left\{ {\begin{array}{*{20}{c}} {\dot x(t) = \lambda - dx(t) - \frac{{\beta x(t)v(t)}}{{1 + \alpha v(t)}}, } \hfill \\ {\dot \omega (t) = \frac{{(1 - q)\beta x(t)v(t)}}{{1 + \alpha v(t)}} - e\omega (t) - \delta \omega (t), } \hfill \\ {\dot y(t) = \frac{{q\beta x(t)v(t)}}{{1 + \alpha v(t)}} - ay(t) + \delta \omega (t), } \hfill \\ {\dot v(t) = ky(t) - uv(t).} \hfill \\ \end{array}} \right.$ | (2) |
其中:
本文考虑了具有潜伏感染细胞和饱和发生率的时滞HIV-1传染病模型:
| $\left\{ {\begin{array}{*{20}{c}} {\dot x(t) = \lambda - dx(t) - \frac{{\beta x(t)v(t)}}{{1 + \alpha v(t)}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \hfill \\ {\dot \omega (t) = \frac{{(1 - q)\beta x(t - {\tau _1})v(t - {\tau _1})}}{{1 + \alpha v(t - {\tau _1})}} - e\omega (t) - \delta \omega (t), } \hfill \\ {\dot y(t) = \frac{{q\beta x(t - {\tau _2})v(t - {\tau _2})}}{{1 + \alpha v(t - {\tau _2})}} - ay(t) + \delta \omega (t), \;\;\;\;\;\;\;\;} \hfill \\ {\dot v(t) = ky(t) - uv(t).{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \hfill \\ \end{array}} \right.$ | (3) |
其中:时滞
系统(3)满足初始条件:
| $\left\{ {\begin{array}{*{20}{c}} {x(\theta ) = {\phi _1}(\theta ), \quad \omega (\theta ) = {\phi _2}(\theta ), \quad y(\theta ) = {\phi _3}(\theta ), \quad v(\theta ) = {\phi _4}(\theta ), } \hfill \\ {{\phi _i}(\theta ) \ge 0, \;\quad \theta \in [ - \tau , 0], \quad {\phi _i}(0) > 0\;(i = 1, 2, 3, 4).\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \hfill \\ \end{array}} \right.$ | (4) |
其中:
显然, 系统(3)总有一个无病平衡点
| $ \begin{align*} R_0 = \frac{k\lambda \beta (eq+\delta )}{adu(e+\delta )}. \end{align*} $ |
当
| $ \begin{align*} x^\ast = \frac{\lambda (1+\alpha v^\ast )}{d(1+\alpha v^\ast )+\beta v^\ast }, \quad \omega ^\ast = \frac{\lambda \beta (1-q)v^\ast }{(e+\delta )[d(1+\alpha v^\ast )+\beta v^\ast ]}, \quad y^\ast = \frac{uv^\ast }{k}, \quad v^\ast = \frac{d}{\beta +\alpha d}(R_0 -1). \end{align*} $ |
关于平衡点的局部稳定性, 我们讨论以下三种情况, 即(ⅰ)
定理 1 (Ⅰ)当
证 明 (Ⅰ)系统(3)在
| $ \begin{align} (s+d)\left[ {s^3+p_2 s^2+p_1 s+p_0 +r_0\mathrm e^{-s\tau _1 }+(q_1 s+q_0 )\mathrm e^{-s\tau _2 }} \right] = 0. \end{align} $ | (5) |
其中:
| $ \begin{align*} &p_0 = au(e+\delta ); \quad p_1 = (e+\delta )(a+u)+au; \quad p_2 = e+\delta +a+u;\\ &r_0 = -\delta (1-q)k\beta x_0; \quad q_0 = -(e+\delta )qk\beta x_0 ; \quad q_1 = -qk\beta x_0. \end{align*} $ |
显然, 方程(5)总有负实根
| $ \begin{align} f(s) = s^3+p_2 s^2+p_1 s+p_0 +r_0 \mathrm e^{-s\tau _1 }+(q_1 s+q_0 )\mathrm e^{-s\tau _2 } = 0. \end{align} $ | (6) |
下面分三种情形来讨论.
(ⅰ)
此时, 方程(6)变为
| $ \begin{align} f(s) = s^3+p_2 s^2+p_1 s+p_0 +r_0 +(q_1 s+q_0 ) \mathrm e^{-s\tau _2 } = 0, \end{align} $ | (7) |
令
| $ \left\{ {\begin{array}{*{20}{c}} {\omega ^3-p_1 \omega = q_1 \omega \cos (\omega \tau _2) -q_0 \sin (\omega \tau _2) , } \hfill \\ {p_2 \omega ^2-p_0 -r_0 = q_1 \omega \sin (\omega \tau _2) +q_0 \cos (\omega \tau _2).}\end{array}} \right.$ | (8) |
再将方程组(8)的两个方程分别平方后相加得
| $ \begin{align} \omega ^6+(p_2^2 -2p_1 )\omega ^4+[p_1^2 -2(p_0 +r_0 )p_2 -q_1^2 ]\omega ^2+(p_0 +r_0 )^2-q_0^2 = 0. \end{align} $ | (9) |
令
| $ \begin{align} z^3+(p_2^2 -2p_1 )z^2+[p_1^2 -2(p_0 +r_0 )p_2 -q_1^2 ]z+(p_0 +r_0 )^2-q_0^2 = 0. \end{align} $ | (10) |
由于
| $ \begin{align*} p_2^2 -2p_1 = \, &(e+\delta +a+u)^2-2[(e+\delta )(a+u)+au] \\&= (e+\delta )^2+a^2+u^2>0, \\ p_1^2 -2(p_0 +r_0 )p_2 -q_1^2 = \, &(e+\delta )^2(a^2+u^2)+2(1-q)\delta (e+\delta +a+u)k\beta x_0\\ & +(au)^2-(qk\beta x_0 )^2 \\ >\, &(e+\delta )^2(a^2+u^2)+(au)^2(1-R_0 ^2)>0, \\ p_0^2 -q_0^2 = \, &[au(e+\delta )]^2-[(e+\delta )qk\beta x_0 ]^2>[au(e+\delta )]^2(1-R_0 ^2)>0, \end{align*} $ |
| $ \begin{align*} &(p_2^2 -2p_1 )(p_1^2 -2p_0 p_2 -q_1^2 )-(p_0^2 -q_0^2 ) \\ = \, &\left[ {(e+\delta )^2+a^2+u^2} \right]\cdot \left[ {(e+\delta )^2(a^2+u^2)+2(1-q)\delta (e+\delta +a+u)k\beta x_0 } \right] \\ &+(a^2+u^2)\left[ {(au)^2-(qk\beta x_0 )^2} \right]>0. \end{align*} $ |
由Routh-Hurwitz准则得, 方程(10)的所有特征值均具有负实部, 这与
(ⅱ)
此时, 方程(6)变为
| $ \begin{align} f(s) = s^3+p_2 s^2+(p_1 +q_1 )s+p_0 +q_0 +r_0\mathrm e^{-s\tau _1 } = 0. \end{align} $ | (11) |
令
| $ \left\{ {\begin{array}{*{20}{c}} {\omega ^3-(p_1 +q_1 )\omega = r_0 \sin (\omega \tau _1 ), } \\ {-p_2 \omega ^2+p_0 +q_0 = r_0 \cos (\omega \tau _1) . }\end{array}} \right.$ | (12) |
再将方程组(12)的两个方程分别平方后相加得
| $ \begin{align} \omega ^6+\left[ {p_2^2 -2(p_1 +q_1 )} \right]\omega ^4+\left[ {(p_1 +q_1 )^2-2(p_0 +q_0 )p_2 } \right]\omega ^2+(p_0 +q_0 )^2-r_0^2 = 0. \end{align} $ | (13) |
令
| $ \begin{align} z^3+\left[ {p_2^2 -2(p_1 +q_1 )} \right]z^2+\left[ {(p_1 +q_1 )^2-2(p_0 +q_0 )p_2 } \right]z+(p_0 +q_0 )^2-r_0^2 = 0. \end{align} $ | (14) |
由于
| $ \begin{align*} p_2^2 -2(p_1 +q_1 ) = (e+\delta )^2+a^2+u^2+2qk\beta x_0 >0, \end{align*} $ |
| $ \begin{align*} &(p_1 +q_1 )^2-2(p_0 +q_0 )p_2 = (e+\delta )^2(a^2+u^2)+(au)^2+(qk\beta x_0 )^2\\ &\qquad\qquad\qquad\qquad\qquad\quad\quad-2auqk\beta x_0 +2(e+\delta )^2qk\beta x_0 \\ &\qquad\qquad\qquad\qquad\qquad\quad\geqslant (e+\delta )^2(a^2+u^2)+2(e+\delta )^2qk\beta x_0 >0, \\ &(p_0 +q_0 )^2-r_0^2 = (p_0 +q_0 +r_0 )(p_0 +q_0 -r_0 )>\left[ {au(e+\delta )(1-R_0 )} \right]^2, \\ &\left[ {p_2^2 -2(p_1 +q_1 )} \right]\cdot \left[ {(p_1 +q_1 )^2-2(p_0 +q_0 )p_2 } \right]-\left[ {(p_0 +q_0 )^2-r_0^2 } \right]>0. \end{align*} $ |
因此, 当
(ⅲ)
令
| $ \begin{align} f(s) = s^3+p_2 s^2+p_1 s+p_0 +(q_1 s+q_0 +r_0 )\mathrm e^{-s\bar {\tau }} = 0, \end{align} $ | (15) |
令
| $ \left\{ {\begin{array}{*{20}{c}} {\omega ^3-p_1 \omega = q_1 \omega \cos (\omega \bar {\tau })-(q_0 +r_0 )\sin (\omega \bar {\tau }), } \\ {p_2 \omega ^2-p_0 = q_1 \omega \sin (\omega \bar {\tau })+(q_0 +r_0 )\cos (\omega \bar {\tau }).} \end{array}} \right.$ | (16) |
再将方程组(16)的两个方程分别平方后相加得
| $ \begin{align} \omega ^6+(p_2^2 -2p_1 )\omega ^4+(p_1^2 -2p_0 p_2 -q_1^2 )\omega ^2+p_0^2 -(q_0 +r_0 )^2 = 0. \end{align} $ | (17) |
令
| $ \begin{align} z^3+(p_2^2 -2p_1 )z^2+(p_1^2 -2p_0 p_2 -q_1^2 )z+p_0^2 -(q_0 +r_0 )^2 = 0. \end{align} $ | (18) |
由于
| $ \begin{align*} &p_2^2 -2p_1 = (e+\delta )^2+a^2+u^2>0, \\ &p_1^2 -2p_0 p_2 -q_1^2 = (e+\delta )^2(a^2+u^2)+(au)^2-(qk\beta x_0 )^2>(e+\delta )^2(a^2+u^2)\\ &\qquad\qquad\qquad\quad\;\;+(au)^2(1-R_0 ^2)>0, \\ &p_0^2 -(q_0 +r_0 )^2 = a^2u^2(e+\delta )^2(1-R_0 ^2)>0, \\ &(p_2^2 -2p_1 )(p_1^2 -2p_0 p_2 -q_1^2 )-\left[ {p_0^2 -(q_0 +r_0 )^2} \right]>0. \end{align*} $ |
因此, 当
综上可知, 当
(Ⅱ)当
| $ \begin{align*} f(0)& = au(e+\delta )-k\beta x_0 (eq+\delta ) = au(e+\delta )(1-R_0 )<0, \\ \mathop {\lim }\limits_{s\to +\infty } f(s)& = +\infty . \end{align*} $ |
因此, 方程
定理 2 当
证 明 系统(3)在
| $ \begin{align} s^4+a_3 s^3+a_2 s^2+a_1 s+a_0 +(b_1 s+b_0 )\mathrm e^{-s\tau _1 }+(c_2 s^2+c_1 s+c_0 )\mathrm e^{-s\tau _2 } = 0. \end{align} $ | (19) |
其中:
| $ \begin{align*} &a_0 = au(e+\delta )\left( {d+\frac{\beta v^\ast }{1+\alpha v^\ast }} \right); \quad a_1 = au(e+\delta )+[(e+\delta )(a+u)+au]\left( {d+\frac{\beta v^\ast }{1+\alpha v^\ast }} \right); \\ &a_2 = (e+\delta )(a+u)+au+(e+\delta +a+u)\left( {d+\frac{\beta v^\ast }{1+\alpha v^\ast }} \right); \\ & a_3 = e+\delta +a+u+d+\frac{\beta v^\ast }{1+\alpha v^\ast }; \\ &b_0 = \frac{-d\delta (1-q)k\beta x^\ast }{(1+\alpha v^\ast )^2}; \quad b_1 = \frac{-\delta (1-q)k\beta x^\ast }{(1+\alpha v^\ast )^2}; \\ &c_0 = \frac{-d(e+\delta )qk\beta x^\ast }{(1+\alpha v^\ast )^2}; \quad c_1 = \frac{-(d+e+\delta )qk\beta x^\ast }{(1+\alpha v^\ast )^2}; \quad c_2 = \frac{-d(e+\delta )qk\beta x^\ast }{(1+\alpha v^\ast )^2}. \end{align*} $ |
下面分三种情形来讨论.
(ⅰ)
此时, 方程(19)变为
| $ \begin{align} s^4+a_3 s^3+a_2 s^2+(a_1 +b_1 )s+a_0 +b_0 +(c_2 s^2+c_1 s+c_0 )\mathrm e^{-s\tau _2 } = 0. \end{align} $ | (20) |
令
| $ \left\{ {\begin{array}{*{20}{c}} {\omega ^4-a_2 \omega ^2+(a_0 +b_0 ) = -c_1 \omega \sin (\omega \tau _2) +(c_2 \omega ^2-c_0 )\cos (\omega \tau _2 ), } \hfill \\ {-a_3 \omega ^3+(a_1 +b_1)\omega = -c_1 \omega \cos (\omega \tau _2) -(c_2 \omega ^2-c_0 )\sin (\omega \tau _2).} \end{array}} \right.$ | (21) |
将方程组(21)的两个方程分别平方后再相加得
| $ \begin{align} \omega ^8+m_3 \omega ^6+m_2 \omega ^4+m_1 \omega ^2+m_0 = 0. \end{align} $ | (22) |
其中:
| $ \begin{align*} &m_0 = (a_0 +b_0 )^2-c_0^2 ; \quad m_1 = (a_1 +b_1 )^2-2(a_0 +b_0 )a_2 -c_1^2 +2c_0 c_2 ; \\ &m_2 = a_2^2 +2(a_0 +b_0 )-2(a_1 +b_1 )a_3 -c_2^2; \\ &m_3 = a_3^2 -2a_2 = (e+\delta )^2+a^2+u^2+\left( {d+\frac{\beta v^\ast }{1+\alpha v^\ast }} \right)^2. \end{align*} $ |
令
| $ \begin{align} z^4+m_3 z^3+m_2 z^2+m_1 z+m_0 = 0. \end{align} $ | (23) |
经计算,
| $ \begin{align*} \Delta _1 = m_3 >0, \quad \Delta _2 = \left| {{\begin{array}{*{20}c} {m_3 } \hfill & 1 \hfill \\ {m_1 } \hfill & {m_2 } \hfill \\ \end{array} }} \right|>0, \quad \Delta _3 = \left| {{\begin{array}{*{20}c} {m_3 } \hfill & 1 \hfill & 0 \hfill \\ {m_1 } \hfill & {m_2 } \hfill & {m_3 } \hfill \\ 0 \hfill & {m_0 } \hfill & {m_1 } \hfill \\ \end{array} }} \right|>0, \quad \Delta _4 = m_0 \Delta _3 >0. \end{align*} $ |
由Routh-Hurwitz判别准则知, 方程(23)的所有特征值均具有负实部, 这与
(ⅱ)
此时, 方程(19)变为
| $ \begin{align} s^4+a_3 s^3+(a_2 +c_2 )s^2+(a_1 +c_1 )s+a_0 +c_0 +(b_1 s+b_0 )\mathrm e^{-s\tau _1 } = 0. \end{align} $ | (24) |
类似于情形(ⅰ)的讨论可知, 方程(24)的任意根均具有负实部.所以, 当
(ⅲ)
令
| $ \begin{align} s^4+a_3 s^3+a_2 s^2+a_1 s+a_0 +\left[ {c_2 s^2+(b_1 +c_1 )s+(b_0 +c_0 )} \right]\mathrm e^{-s\bar {\tau }} = 0. \end{align} $ | (25) |
类似于情形(ⅰ)的讨论可知, 方程(25)的任意根均具有负实部.所以, 当
综上可知, 当
定理 3 当
证 明 构造Lyapunov函数
| $ \begin{align*} V_1 (t) = \, &x_0 \left( {\frac{x(t)}{x_0 }-1-\ln \frac{x(t)}{x_0 }} \right)+\frac{k\lambda \beta \delta }{adu(e+\delta )}\omega (t)+\frac{k\lambda \beta }{adu}y(t)+\frac{\lambda \beta }{du}v(t) \\ &+\frac{k\lambda \beta \delta }{adu(e+\delta )}\int_{t-\tau _1 }^t {\frac{(1-q)\beta x(\theta )v(\theta )}{1+\alpha v(\theta )}} \mathrm{d}\theta +\frac{k\lambda \beta }{adu}\int_{t-\tau _2 }^t {\frac{q\beta x(\theta )v(\theta )}{1+\alpha v(\theta )}} \mathrm{d}\theta . \end{align*} $ |
计算函数
| $ \begin{align} \frac{\rm d}{\mathrm dt}V_1 (t) = \, &\left( {1-\frac{x_0 }{x(t)}} \right)\left( {\lambda -dx(t)-\frac{\beta x(t)v(t)}{1+\alpha v(t)}} \right)\\ &+\frac{k\lambda \beta \delta }{adu(e+\delta )}\left( {\frac{(1-q)\beta x(t-\tau _1 )v(t-\tau _1 )}{1+\alpha v(t-\tau _1 )}-(e+\delta )\omega (t)} \right) \\ &+\frac{k\lambda \beta }{adu}\left( {\frac{q\beta x(t-\tau _2 )v(t-\tau _2 )}{1+\alpha v(t-\tau _2 )}-ay(t)+\delta \omega (t)} \right)\\ &+\frac{\lambda \beta }{du}[ky(t)-uv(t)] +\frac{k\lambda \beta \delta }{adu(e+\delta )}\cdot \frac{(1-q)\beta x(t)v(t)}{1+\alpha v(t)}\hfill \\ &-\frac{k\lambda \beta \delta }{adu(e+\delta )}\cdot \frac{(1-q)\beta x(t-\tau _1 )v(t-\tau _1 )}{1+\alpha v(t-\tau _1 )} \hfill \\ &+\frac{k\lambda \beta }{adu}\cdot \frac{q\beta x(t)v(t)}{1+\alpha v(t)}-\frac{k\lambda \beta }{adu}\cdot \frac{q\beta x(t-\tau _2 )v(t-\tau _2 )}{1+\alpha v(t-\tau _2 )}. \end{align} $ | (26) |
由于
| $ \begin{align*} \frac{\rm d}{\mathrm dt}V_1 (t) = \, &-\frac{d}{x(t)}\left( {x(t)-x_0 } \right)^2+(R_0 -1)\frac{\beta x(t)v(t)}{1+\alpha v(t)}+\left( {\frac{1}{1+\alpha v(t)}-1} \right)\beta x_0 v(t) \\ = \, &-\frac{d}{x(t)}\left( {x(t)-x_0 } \right)^2+(R_0 -1)\frac{\beta x(t)v(t)}{1+\alpha v(t)}-\frac{\alpha \beta x_0 v^2(t)}{1+\alpha v(t)}. \end{align*} $ |
若
定理 4 当
证 明 定义函数
| $ \begin{align*} F:{\bf R}(>0)\to {\bf R}(\geqslant 0), \quad F(z) = z-1-\ln z, \end{align*} $ |
易知, 对
构造Lyapunov函数
| $ \begin{align*} V_2 (t) = \, &x^\ast F\left( {\frac{x(t)}{x^\ast }} \right)+\frac{\delta }{eq+\delta }\omega ^\ast F\left( {\frac{\omega (t)}{\omega ^\ast }} \right)\\ &+\frac{e+\delta }{eq+\delta }y^\ast F\left( {\frac{y(t)}{y^\ast }} \right)+\frac{a(e+\delta )}{k(eq+\delta )}v^\ast F\left( {\frac{v(t)}{v^\ast }} \right) \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\int_{t-\tau _1 }^t {F\left( {\frac{(1+\alpha v^\ast)x(\theta)v(\theta)}{x^\ast v^\ast(1+\alpha v(\theta))}} \right)} \;\mathrm {d}\theta \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\int_{t-\tau _2 }^t {F\left( {\frac{(1+\alpha v^\ast)x(\theta)v(\theta)}{x^\ast v^\ast(1+\alpha v(\theta))}} \right)} \mathrm {d}\theta . \end{align*} $ |
计算函数
| $ \begin{align} \frac{\rm d}{\mathrm dt}V_2 (t) = \, &\left( {1-\frac{x^\ast }{x(t)}} \right)\left( {\lambda -dx(t)-\frac{\beta x(t)v(t)}{1+\alpha v(t)}} \right) \\ &+\frac{\delta }{eq+\delta }\left( {1-\frac{\omega ^\ast }{\omega (t)}} \right)\left( {\frac{(1-q)\beta x(t-\tau _1 )v(t-\tau _1 )}{1+\alpha v(t-\tau _1 )}-(e+\delta )\omega (t)} \right) \\ &+\frac{e+\delta }{eq+\delta }\left( {1-\frac{y^\ast }{y(t)}} \right)\left( {\frac{q\beta x(t-\tau _2 )v(t-\tau _2 )}{1+\alpha v(t-\tau _2 )}-ay(t)+\delta \omega (t)} \right) \\ &+\frac{a(e+\delta )}{k(eq+\delta )}\left( {1-\frac{v^\ast }{v(t)}} \right)[ky(t)-uv(t)] \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x(t)v(t)}{1+\alpha v(t)}-\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x(t-\tau _1 )v(t-\tau _1 )}{1+\alpha v(t-\tau _1 )} \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _1 )} \right)} \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x(t)v(t)}{1+\alpha v(t)}-\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x(t-\tau _2 )v(t-\tau _2 )}{1+\alpha v(t-\tau _2 )} \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _2 )} \right)}. \end{align} $ | (27) |
将
| $ \begin{align} \frac{\rm d}{\mathrm dt}V_2 (t) = \, &\left( {1-\frac{x^\ast }{x(t)}} \right)\left( {-d\left( {x(t)-x^\ast } \right)+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }} \right)-\frac{\beta x(t)v(t)}{1+\alpha v(t)}\\ &+\frac{\beta x^\ast v(t)}{1+\alpha v(t)} -\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\omega ^\ast }{\omega (t)}\cdot \frac{\beta x(t-\tau _1 )v(t-\tau _1 )}{1+\alpha v(t-\tau _1 )}+\frac{\delta (e+\delta )}{eq+\delta }\omega ^\ast \\ &-\frac{(e+\delta )q}{eq+\delta }\cdot \frac{y^\ast }{y(t)}\cdot \frac{\beta x(t-\tau _2 )v(t-\tau _2 )}{1+\alpha v(t-\tau _2 )}+\frac{a(e+\delta )}{eq+\delta }y^\ast \\ &+\frac{\delta (e+\delta )}{eq+\delta }\cdot \frac{y^\ast }{y(t)}\omega (t) -\frac{a(e+\delta )u}{k(eq+\delta )}v(t)-\frac{a(e+\delta )}{(eq+\delta )}\cdot \frac{v^\ast }{v(t)}y(t)\\ &+\frac{a(e+\delta )}{k(eq+\delta )}uv^\ast +\frac{\delta }{eq+\delta }\cdot\frac{(1-q)\beta x(t)v(t)}{1+\alpha v(t)}+\frac{e+\delta }{eq+\delta }\cdot\frac{q\beta x(t)v(t)}{1+\alpha v(t)} \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _1 )} \right)} \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _2 )} \right)}. \end{align} $ | (28) |
由于
| $ \begin{align*} \frac{\delta }{eq+\delta }\cdot \frac{(1-q)\beta x(t)v(t)}{1+\alpha v(t)}+\frac{e+\delta }{eq+\delta }\cdot \frac{q\beta x(t)v(t)}{1+\alpha v(t)} = \frac{\beta x(t)v(t)}{1+\alpha v(t)}, \end{align*} $ |
所以式(28)可化为
| $ \begin{align*} \frac{\rm d}{\mathrm dt}V_2 (t) = \, &-\frac{d\left( {x(t)-x^\ast } \right)^2}{x(t)}+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }-\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{x^\ast }{x(t)}+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{(1+\alpha v^\ast )v(t)}{(1+\alpha v(t))v^\ast } \\ &-\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{\omega ^\ast }{\omega (t)}\cdot \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v^\ast } \right)}{x^\ast v^\ast \left( {1+\alpha v(t-\tau _1 )} \right)}+\frac{\delta (e+\delta )}{eq+\delta }\omega ^\ast \\ &-\frac{(e+\delta )q}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{y^\ast }{y(t)}\cdot \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v^\ast } \right)}{x^\ast v^\ast \left( {1+\alpha v(t-\tau _2 )} \right)}+\frac{a(e+\delta )}{eq+\delta }y^\ast \\ &+\frac{\delta (e+\delta )\omega ^\ast }{eq+\delta }\cdot \frac{y^\ast }{y(t)}\cdot \frac{\omega (t)}{\omega ^\ast } -\frac{a(e+\delta )uv^\ast }{k(eq+\delta )}\cdot \frac{v(t)}{v^\ast } \\ &-\frac{ay^\ast (e+\delta )}{(eq+\delta )}\cdot \frac{v^\ast }{v(t)}\cdot \frac{y(t)}{y^\ast }+\frac{a(e+\delta )}{k(eq+\delta )}uv^\ast \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _1 )} \right)} \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _2 )} \right)}. \end{align*} $ |
注意到
| $ \begin{align*} (e+\delta )\omega ^\ast = \frac{(1-q)\beta x^\ast v^\ast }{1+\alpha v^\ast }, \quad ay^\ast = \frac{q\beta x^\ast v^\ast }{1+\alpha v^\ast }+\delta \omega ^\ast , \quad y^\ast = \frac{uv^\ast }{k}, \end{align*} $ |
则
| $ \begin{align*} \frac{\rm d}{\mathrm dt}V_2 (t) = \, &-\frac{d\left( {x(t)-x^\ast } \right)^2}{x(t)}+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }-\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{x^\ast }{x(t)}+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{(1+\alpha v^\ast )v(t)}{(1+\alpha v(t))v^\ast } \\ &-\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{\omega ^\ast }{\omega (t)}\cdot \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v^\ast } \right)}{x^\ast v^\ast \left( {1+\alpha v(t-\tau _1 )} \right)}\\ &+\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast } -\frac{(e+\delta )q}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{y^\ast }{y(t)}\cdot \\ & \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v^\ast } \right)}{x^\ast v^\ast \left( {1+\alpha v(t-\tau _2 )} \right)}+\frac{e+\delta }{eq+\delta }\cdot \left( {\frac{q\beta x^\ast v^\ast }{1+\alpha v^\ast }+\delta \omega ^\ast } \right) \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{y^\ast }{y(t)}\cdot \frac{\omega (t)}{\omega ^\ast } -\frac{e+\delta }{eq+\delta }\cdot \left( {\frac{q\beta x^\ast v^\ast }{1+\alpha v^\ast }+\delta \omega ^\ast } \right)\cdot \frac{v(t)}{v^\ast } \\ &-\frac{e+\delta }{eq+\delta }\cdot \left( {\frac{q\beta x^\ast v^\ast }{1+\alpha v^\ast }+\delta \omega ^\ast } \right)\cdot \frac{v^\ast }{v(t)}\cdot \frac{y(t)}{y^\ast }+\frac{e+\delta }{eq+\delta }\cdot \left( {\frac{q\beta x^\ast v^\ast }{1+\alpha v^\ast }+\delta \omega ^\ast } \right) \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _1 )} \right)} \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _2 )} \right)} \end{align*} $ |
| $ \begin{align*} = \, &-\frac{d\left( {x(t)-x^\ast } \right)^2}{x(t)}+\frac{3\beta x^\ast v^\ast }{1+\alpha v^\ast }-\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{x^\ast }{x(t)}+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{(1+\alpha v^\ast )v(t)}{(1+\alpha v(t))v^\ast } \\ &-\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{\omega ^\ast }{\omega (t)}\cdot \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v^\ast } \right)}{x^\ast v^\ast \left( {1+\alpha v(t-\tau _1 )} \right)}+\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast } \\ &-\frac{(e+\delta )q}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{y^\ast }{y(t)}\cdot \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v^\ast } \right)}{x^\ast v^\ast \left( {1+\alpha v(t-\tau _2 )} \right)} \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{y^\ast }{y(t)}\cdot \frac{\omega (t)}{\omega ^\ast } -\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{v(t)}{v^\ast } -\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{v^\ast }{v(t)}\cdot \frac{y(t)}{y^\ast } \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _1 )} \right)} \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _2 )} \right)}. \end{align*} $ |
由于
| $ \begin{align*} \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast } = \frac{\delta (1-q)}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }+\frac{(e+\delta )q}{eq+\delta }\cdot \frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }, \end{align*} $ |
那么
| $ \begin{align} \frac{\rm d}{\mathrm dt}V_2 (t) = \, &-\frac{d\left( {x(t)-x^\ast } \right)^2}{x(t)}+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\Bigg( 4-\frac{x^\ast }{x(t)}-\frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v^\ast } \right)y^\ast }{x^\ast v^\ast \left( {1+\alpha v(t-\tau _2 )} \right)y(t)} \hfill \\ &-\frac{v^\ast y(t)}{v(t)y^\ast }-\frac{1+\alpha v(t)}{1+\alpha v^\ast } \Bigg) +\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\Bigg(5-\frac{x^\ast }{x(t)} \hfill \\ &-\frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v^\ast } \right)\omega ^\ast }{x^\ast v^\ast \left( {1+\alpha v(t-\tau _1 )} \right)\omega (t)}-\frac{y^\ast \omega (t)}{y(t)\omega ^\ast }-\frac{v^\ast y(t)}{v(t)y^\ast }-\frac{1+\alpha v(t)}{1+\alpha v^\ast }\Bigg) \\ &+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{1+\alpha v(t)}{1+\alpha v^\ast }-\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{(1+\alpha v^\ast )v(t)}{(1+\alpha v(t))v^\ast }-\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{v(t)}{v^\ast } \\ &+\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _1 )} \right)} \\ &+\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast}{1+\alpha v^\ast}\ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _2 )} \right)}. \end{align} $ | (29) |
注意到
| $ \begin{align*} &\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{1+\alpha v(t)}{1+\alpha v^\ast }-\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }+\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{(1+\alpha v^\ast )v(t)}{(1+\alpha v(t))v^\ast }-\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\cdot \frac{v(t)}{v^\ast } \hfill \\ = \, &-\frac{\alpha \beta x^\ast (v-v^\ast )^2}{(1+\alpha v^\ast )^2(1+\alpha v(t))}, \end{align*} $ |
| $ \begin{align*} \ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _1 )} \right)} = \, &\ln \frac{x^\ast }{x(t)}+\ln \frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v^\ast } \right)\omega ^\ast }{x^\ast v^\ast \left( {1+\alpha v(t-\tau _1 )} \right)\omega (t)}\\ &+\ln \frac{y^\ast \omega (t)}{y(t)\omega ^\ast } \hfill +\ln \frac{v^\ast y(t)}{v(t)y^\ast }+\ln \frac{1+\alpha v(t)} {1+\alpha v^\ast }, \\ \ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v(t)} \right)}{x(t)v(t)\left( {1+\alpha v(t-\tau _2 )} \right)} = \, & \ln \frac{x^\ast }{x(t)}+\ln \frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v^\ast } \right)y^\ast }{x^\ast v^\ast \left( {1+\alpha v(t-\tau _2 )} \right)y(t)} \hfill \\ &+\ln \frac{v^\ast y(t)}{v(t)y^\ast }+\ln \frac{1+\alpha v(t)}{1+\alpha v^\ast }. \end{align*} $ |
于是式(29)化为
| $ \begin{align*} \frac{\rm d}{\mathrm dt}V_2 (t) = \, &-\frac{d\left( {x(t)-x^\ast } \right)^2}{x(t)}-\frac{\alpha \beta x^\ast (v-v^\ast )^2}{(1+\alpha v^\ast )^2(1+\alpha v(t))} \\ &-\frac{(e+\delta )q}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\left[ F\left( {\frac{x^\ast }{x(t)}} \right)+F\left( {\frac{x(t-\tau _2 )v(t-\tau _2 )\left( {1+\alpha v^\ast } \right)y^\ast }{x^\ast v^\ast \left( {1+\alpha v(t-\tau _2 )} \right)y(t)}} \right)\right.\\ &\left.+F\left( {\frac{v^\ast y(t)}{v(t)y^\ast }} \right)+F\left( {\frac{1+\alpha v(t)}{1+\alpha v^\ast }} \right) \right]\\ & -\frac{\delta (1-q)}{eq+\delta }\cdot\frac{\beta x^\ast v^\ast }{1+\alpha v^\ast }\left[ F\left( {\frac{x^\ast }{x(t)}} \right)+F\left( {\frac{x(t-\tau _1 )v(t-\tau _1 )\left( {1+\alpha v^\ast } \right)\omega ^\ast }{x^\ast v^\ast \left( {1+\alpha v(t-\tau _1 )} \right)\omega (t)}} \right)+F\left( {\frac{y^\ast \omega (t)}{y(t)\omega ^\ast }} \right)\right.\\ &\left.+F\left( {\frac{v^\ast y(t)}{v(t)y^\ast }} \right)+F\left( {\frac{1+\alpha v(t)}{1+\alpha v^\ast }} \right) \right]. \end{align*} $ |
由于
在系统(3)中, 若令参数
| $ \begin{align*} &\lambda = 10, \quad d = 0.1, \quad\beta = 0.001, \quad\alpha = 0.01, \quad q = 0.8, \quad e = 0.3, \\ &\delta = 0.5, \quad a = 0.5, \quad k = 0.4, \quad u = 3, \quad \tau _1 = 3, \quad\tau _2 = 8, \end{align*} $ |
则基本再生数
| $ \begin{align*} R_0 = \frac{k\lambda \beta (eq+\delta )}{adu(e+\delta )}\approx \mathrm {0.024\; 7}<1, \end{align*} $ |
由定理3知, 系统(3)的无病平衡点
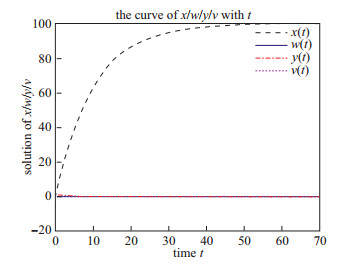
|
图 1 当 |
若令参数
| $ \begin{align*} &\lambda = 250, \quad d = 0.005, \quad \beta = 0.001, \quad \alpha = 0.003, \quad q = 0.6, \quad e = 0.3, \quad \delta = 0.5, \\ &a = 0.5, \quad k = 0.4, \quad u = 0.3, \quad \tau _1 = 3, \quad \tau _2 = 8, \end{align*} $ |
此时基本再生数
| $ \begin{align*} R_0 = \frac{k\lambda \beta (eq+\delta )}{adu(e+\delta )}\approx 113.33>1, \end{align*} $ |
系统(3)有唯一的慢性平衡点
| $ \begin{align*} P^\ast (\mathrm {1173.6}, \, \mathrm { 324.43}, \, \mathrm {415.02}, \, 553.37), \end{align*} $ |
根据定理4可知,

|
图 2 当 |
本文研究了一类具有潜伏感染细胞和饱和发生率的时滞HIV-1传染病模型, 讨论了系统(3)的无病平衡点
| [1] |
孙起麟.艾滋病病毒感染和治疗动力学的理论研究与应用[D].北京: 北京科技大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10008-1015615931.htm
|
| [2] |
王开发, 邱志鹏, 邓国宏. 病毒感染群体动力学模型分析[J]. 系统科学与数学, 2003, 32(4): 433-443. |
| [3] |
PERELSON A S, NELSON P W. Mathematical models of HIV dynamics in vivo[J]. SIAM Review, 1999, 41(1): 3-44. DOI:10.1137/S0036144598335107 |
| [4] |
NOWAK M A, ANDERSON R M, BOERLIJST M C, et al. HIV-1 evolution and disease progression[J]. Science, 1996, 274(5289): 1008-1011. DOI:10.1126/science.274.5289.1008 |
| [5] |
KOROBEINIKOV A. Global properties of basic virus dynamics models[J]. Bulletin of Mathematical Biology, 2004, 66(4): 879-883. DOI:10.1016/j.bulm.2004.02.001 |
| [6] |
NOWAK M A, BANGHAM C R M. Population dynamics of immune responses to persistent viruses[J]. Science, 1996, 272(5258): 74-79. DOI:10.1126/science.272.5258.74 |
| [7] |
SONG X Y, NEUMANN A U. Global stability and periodic solution of the viral dynamics[J]. Journal of Mathematical Analysis and Applications, 2007, 329(1): 281-297. DOI:10.1016/j.jmaa.2006.06.064 |
| [8] |
BEDDINGTON J R. Mutual Interference Between Parasites or Predators and its Effect on Searching Efficiency[J]. Journal of Animal Ecology, 1975, 44(1): 331-340. |
| [9] |
DEANGELIS D L, GOLDSTEIN R A, O'NEILL R V. A model for tropic interaction[J]. Ecology, 1975, 56(4): 881-892. DOI:10.2307/1936298 |
| [10] |
XU R. Global stability of an HIV-1 infection model with saturation infection and intracellular delay[J]. Journal of Mathematical Analysis and Application, 2011, 375(1): 75-81. DOI:10.1016/j.jmaa.2010.08.055 |
| [11] |
GUO T, LIU H H, XU C L, et al. Dynamics of a delayed HIV-1 infection model with saturation incidence rate and CTL immune response[J]. International Journal of Bifurcation and Chaos, 2016, 26(4): 1-26. |
| [12] |
BAGASRA O, POMERANTZ R J. Human immunodeficiency virus type-Ⅰ provirus is demonstrated in peripheral blood monocytes in vivo:A study utilizing an in situ polymerase chain reaction[J]. AIDS Research and Human Retroviruses, 1993, 9(1): 69-76. DOI:10.1089/aid.1993.9.69 |
| [13] |
PACE M J, AGOSTO L, GRAF E H. HIV reservoirs and latency models[J]. Virology, 2011, 411(2): 344-354. DOI:10.1016/j.virol.2010.12.041 |
| [14] |
CAPISTRÁN M A. A study of latency, reactivation and apoptosis throughout HIV pathogenesis[J]. Mathematical and Computer Modelling, 2010, 52(7/8): 1011-1015. |
| [15] |
WANG H B, XU R, WANG Z W, et al. Global dynamics of a class of HIV-1 infection models with latently infected cells[J]. Nonlinear Analysis:Modeling and Control, 2015, 20(1): 21-37. DOI:10.15388/NA.2015.1.2 |
| [16] |
HALE J K, LUNEL S V. Introduction to Functional Differential Equations[M]. New York: Springer, 1993.
|




