0 Introduction

Recall that the finite-dimensional simple Lie superalgebras over the field of complex numbers were classified by Kac in the 1970s (cf.[1]). Furthermore, their representation theory was developed extensively.

In recent years, there has been an increasing interest in modular representation theory of restricted Lie superalgebras. A systematical research on modular representation theory was initiated and developed in [2-6] for Lie superalgebras of classical type, and in [7-15] for Lie superalgebras of Cartan type, respectively. W. Wang and L. Zhao^[3] proved a super version of the celebrated Kac-Weisfeiler Property for the classical Lie superalgebras, which by definition admit an even non-degenerate supersymmetric bilinear form and whose even subalgebras are reductive. In [7-15], all simple restricted and some simple non-restricted modules of Lie superalgebras of Cartan type were classified. Moreover, character formulas for these simple modules were given.

In this paper, we study the modular representations of finite-dimensional Lie superalgebras. This research is largely motivated by [3, 16, 17]. We briefly introduce the structure of this paper. We collect the general notations and elementary preliminaries on Lie (associative) superalgebras in Section 1. Then Section 2 is devoted to developing general representation theory for a finite-dimensional Lie superalgebra $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ over an algebraically closed field $\mathbb{F}$ of characteristic $p>2$. We show that each simple $\mathfrak{g}$-module is of finite-dimensional, and there exists an upper bound on the dimensions of simple modules. Moreover, $\mathfrak{g}$ has a finite-dimensional p-envelope which is a restricted Lie superalgebra. In some sense, this helps us to reduce representations of finite-dimensional Lie superalgebras to those of restricted ones. We then study irreducible representations of finite-dimensional restricted Lie superalgebras in Section 3. We give a criterion for simplicity of an induced module of a finite-dimensional restricted Lie superalgebra $\mathfrak{g}$, and obtain a bijection between the isomorphism classes of simple modules of $\mathfrak{g}$ and those of some restricted subalgebra (cf. Theorem 3.12). This reduces simple $\mathfrak{g}$-modules to those simple modules of a certain restricted subalgebra.

1 Notations and preliminaries

In this paper, we always assume that the ground field $\mathbb{F}$ is algebraically closed and of prime characteristic $p> 2$. We exclude the case $p=2$, since in this case, Lie superalgebras coincide with $\mathbb{Z}_2$-graded Lie algebras.

1.1 Basic definitions

A superspace is a $\mathbb{Z}_2$-graded vector space $V=V_{\bar{0}}\oplus V_{\bar{1}}$, in which we call elements in $V_{\bar{0}}$ and $V_{\bar{1}}$ even and odd, respectively. We usually write $|v|\in{\mathbb{Z}}_2$ for the parity (or degree) of $v\in V$, which is implicitely assumed to be $\mathbb{Z}_2$-homogeneous. A superalgebra is a $\mathbb{Z}_2$-graded vector space ${\mathfrak{A}}={\mathfrak{A}}_{\bar{0}}\oplus {\mathfrak{A}}_{\bar{1}}$ endowed with an algebra structure ``$\cdot$" such that ${\mathfrak{A}}_{\alpha}\cdot{\mathfrak{A}}_{\beta}\subseteq {\mathfrak{A}}_{\alpha+\beta}$ for any $\alpha,\beta\in {\mathbb{Z}}_2$. A superalgebra $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ with an algebra structure [-, -] is called a Lie superalgebra if for any homogeneous elements $x,y,z$ in $\mathfrak{g}$, the following conditions hold.

(i)$[x,y]=-(-1)^{|x||y|}[y,x]$;

(ii)$[x,[y,z]]=[[x,y],z]+(-1)^{|x||y|}[y,[x,z]]$.

Homomorphisms of superalgebras (Lie superalgebras) are those linear mappings which reserve the $\mathbb{Z}_2$-grading and the superalgebra (Lie superalgebra) structure.

For a Lie superalgebra $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$, it follows from the definition that the even part $\mathfrak{g}_{\bar{0}}$ is a Lie algebra and the odd part $\mathfrak{g}_{\bar{1}}$ is a $\mathfrak{g}_{\bar{0}}$-module under the adjoint action. Let $({\mathfrak{A}},\cdot)$ be an associative superalgebra, we denote $[x,y]:=x\cdot y-(-1)^{|x||y|}y\cdot x$ for any homogeneous elements $x,y\in \mathfrak{A}$. Then $(\mathfrak{A},[-, -])$ is a Lie superalgebra.

Example 1.1 Let $V=V_{\bar{0}}\oplus V_{\bar{1}}$ be a $\mathbb{Z}_2$-graded vector space over $\mathbb{F}$ with $\dim V_{\bar{0}}=m$ and $\dim V_{\bar{1}}=n$. Then the algebra ${\rm End}_{\mathbb{F}}(V)$ consisting of $\mathbb{F}$-linear transformation of V is an associative superalgebra with

${\rm End}_{{\mathbb{F}}}(V)_{\alpha}:=\{A\in {\rm End}_{{\mathbb{F}}}(V)\mid A(V_{\beta})\subseteq V_{\alpha+\beta}, \,\forall\,\beta\in{\mathbb{Z}}_2\},\,\alpha\in\mathbb{Z}_2.$

Moreover, for any homogeneous elements $A,B\in {\rm End}_{{\mathbb{F}}}(V)$, we define a new multiplication [-, -] by

$[A,B]:=AB-(-1)^{|A||B|}BA.$

Then $({\rm End}_{{\mathbb{F}}}(V),[-, -])$ is the so-called general linear Lie superalgebra, denoted by $\mathfrak{g}\mathfrak{l}(V)=\mathfrak{g}\mathfrak{l}(V)_{\bar{0}} \oplus\mathfrak{g}\mathfrak{l}(V)_{\bar{1}}$ or $\mathfrak{g}\mathfrak{l}(m|n)=\mathfrak{g}\mathfrak{l}(m|n)_{\bar{0}} \oplus\mathfrak{g}\mathfrak{l}(m|n)_{\bar{1}}.$ More precisely,

$\begin{align} & \mathfrak{g}\mathfrak{l}{{(m|n)}_{{\bar{0}}}}=\left\{ \left( \begin{matrix} A & 0 \\ 0 & D \\ \end{matrix} \right)|A\in \text{Ma}{{\text{t}}_{m\times m}},D\in \text{Ma}{{\text{t}}_{n\times n}} \right\}, \\ & \mathfrak{g}\mathfrak{l}{{(m|n)}_{{\bar{1}}}}=\left\{ \left( \begin{matrix} 0 & B \\ C & 0 \\ \end{matrix} \right)|B\in \text{Ma}{{\text{t}}_{m\times n}},C\in \text{Ma}{{\text{t}}_{n\times m}} \right\}, \\ \end{align}$

where Mat$_{i\times j}$ denotes the set of all $i\times j$ matrices for $i,j\in{\mathbb{N}}\backslash \{0\}$.

Definition 1.2 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a Lie superalgebra. A $\mathbb{Z}_2$-graded vector space $V=V_{\bar{0}}\oplus V_{\bar{1}}$ is called a $\mathfrak{g}$-module if there exists a Lie superalgebra homomorphism from $\mathfrak{g}$ to $\mathfrak{g}\mathfrak{l}(V)$.

Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a Lie superalgebra. Denote by $U(\mathfrak{g})$ the universal enveloping superalgebra of $\mathfrak{g}$, which is the quotient of the tensor superalgebra $T(\mathfrak{g})$ by the ideal generated by $[x,y]-xy+(-1)^{|x||y|}yx$ for any $x, y\in\mathfrak{g}_{\bar{0}}\cup\mathfrak{g}_{\bar{1}}$. Set $Z(\mathfrak{g})=\{u\in U(\mathfrak{g})_{\bar{0}}\mid uv=vu,\,\forall\,v\in U(\mathfrak{g})\}$ which is called the even center of $U(\mathfrak{g})$.

In this paper, all Lie superalgebras are assumed to be finite-dimensional. By vector spaces, subalgebras, ideals, submodules etc., we mean in the super sense unless otherwise stated.

1.2 Key lemmas

In this subsection, we present several lemmas for later use. Let $\mathfrak{A}=\mathfrak{A}_{\bar{0}}\oplus\mathfrak{A}_{\bar{1}}$ be a superalgebra. For elements $y,z_1,\cdots,z_n$ in $\mathfrak{A}$ and

${\bf{s}} = ({s_1}, \cdots ,{s_n}),{\bf{t}} = ({t_1}, \cdots ,{t_n}) \in {\mathbb{N}^n},$

set

${\mathbf{z}}:=(z_1,\cdots,z_n)\in {\mathfrak{A}}^n , {\mathbf{z}}^{{\mathbf{s}}}:=z_1^{s_1}\cdots z_n^{s_n}\in\mathfrak{A},$

and

$\{y,{\mathbf{z}};{\mathbf{t}}\}:=[\cdots[\cdots[\cdots[[\cdots[y, \underbrace{z_1],\cdots,z_1]}_{t_1{\rm times}},\underbrace{z_2],\cdots ,z_2]}_{t_2\,{\rm times}},\cdots, \underbrace{z_n],\cdots,z_n]}_{t_n\,{\rm times}}\in\mathfrak{A}$

with the convention that $\{y,{\mathbf{z}};{\mathbf{0}}\}=y$. Let

$|\mathbf{s}|:=\sum\limits_{i=1}^n s_i,{\mathbf{s}\choose \mathbf{t}}:=\prod\limits_{i=1}^n{s_i\choose t_i}.$

We define a partial order ``$\preccurlyeq$" on $\mathbb{N}^n$ as follows.

${\mathbf{t}}\preccurlyeq{\mathbf{s}}\;{\rm if\;and\;only\;if}\;t_i\leq s_i,\forall\,1\leq i\leq n.$

Lemma 1.3 Assume $\mathfrak{A}=\mathfrak{A}_{\bar{0}}\oplus\mathfrak{A}_{\bar{1}}$ is an associative superalgebra. Let $y\in\mathfrak{A}_{\bar{0}}\cup\mathfrak{A}_{\bar{1}}$, $z_1,\cdots, z_m\in\mathfrak{A}_{\bar{0}}$ and $z_{m+1},\cdots, z_n\in\mathfrak{A}_{\bar{1}}$. Let ${\mathbf{s}}=(s_1,\cdots, s_n)\in\mathbb{N}^n$ with $s_i\in\{0,1\}$ for $m+1\leq i\leq n$. Then

$y{\mathbf{z}}^{{\mathbf{s}}}=\sum\limits_{{\mathbf{0}}\preccurlyeq {\mathbf{t}}\preccurlyeq{\mathbf{s}}}\pm{{\mathbf{s}}\choose {\mathbf{\mathbf{t}}}}{\mathbf{z}}^{{\mathbf{s}}-{\mathbf{\mathbf{t}}}} \{y,{\mathbf{z}};{\mathbf{\mathbf{t}}}\}.$

(1.1)

Proof It is trivial for $\mathbf{s}=\mathbf{0}$. In the following, we assume $\mathbf{s}\neq \mathbf{0}$. For any $x\in\mathfrak{A}_{\bar{0}}$, let $L_x,R_x$ denote the left and right multiplications by x in $\mathfrak{A}$, respectively. Then $R_x=L_x-{\rm ad }x$, and $L_x$ commutes with ${\rm ad} x$. We divide the proof into three cases.

Case 1 $s_{m+1}=s_{m+2}=\cdots=s_n=0$.

In this case, we proceed by induction on m. The case $m=1$ follows from the following computation.

$\begin{array}{l} yz_1^{{s_1}} = \underbrace {{R_{{z_1}}}^\circ {R_{{z_1}}}^\circ \cdots ^\circ {R_{{z_1}}}}_{{s_1}{\kern 1pt} {\rm{times}}}(y)\\ \quad \;\; = {({L_{{z_1}}} - {\rm{ad}}{z_1})^{{s_1}}}(y)\\ \quad \;\; = \sum\limits_{0 \le {t_1} \le {s_1}} {{{( - 1)}^{{t_1}}}} \left( \begin{array}{c} {s_1}\\ {t_1} \end{array} \right)L_{{z_1}}^{{s_1} - {t_1}}{({\rm{ad}}{z_1})^{{t_1}}}(y)\\ \quad \;\; = \sum\limits_{0 \le {t_1} \le {s_1}} {\left( \begin{array}{c} {s_1}\\ {t_1} \end{array} \right)} z_1^{{s_1} - {t_1}}[ \cdots [y,\underbrace {{z_1}], \cdots ,{z_1}]}_{{t_1}{\kern 1pt} {\rm{times}}}. \end{array}$

Assume that $m>1$. Let $y':=yz_1^{s_1}\cdots z_{m-1}^{s_{m-1}},{\mathbf{s}}'=(s_1,\cdots,s_{m-1})$. The induction hypothesis yields

$\begin{align} & y{{\mathbf{s}}^{\mathbf{s}}}={y}'z_{m}^{{{s}_{m}}} \\ & \quad \ \,=\sum\limits_{\mathbf{0}\preccurlyeq {{\mathbf{t}}^{\prime }}\preccurlyeq {{\mathbf{s}}^{\prime }}}{\pm }\left( \begin{matrix} {{\mathbf{s}}^{\prime }} \\ {{\mathbf{t}}^{\prime }} \\ \end{matrix} \right){{\mathbf{z}}^{{{\mathbf{s}}^{\prime }}-{{\mathbf{t}}^{\prime }}}}\{y,\mathbf{z};{{\mathbf{t}}^{\prime }}\}z_{m}^{{{s}_{m}}} \\ & \quad \ \,=\sum\limits_{\mathbf{0}\preccurlyeq {{\mathbf{t}}^{\prime }}\preccurlyeq {{\mathbf{s}}^{\prime }}}{\pm }\left( \begin{matrix} {{\mathbf{s}}^{\prime }} \\ {{\mathbf{t}}^{\prime }} \\ \end{matrix} \right){{\mathbf{z}}^{{{\mathbf{s}}^{\prime }}-{{\mathbf{t}}^{\prime }}}}\sum\limits_{0\le {{t}_{m}}\le {{s}_{m}}}{\pm }\left( \begin{matrix} {{s}_{m}} \\ {{t}_{m}} \\ \end{matrix} \right)z_{m}^{{{s}_{m}}-{{t}_{m}}}\{\{y,\mathbf{z};{{\mathbf{t}}^{\prime }}\},{{z}_{m}};{{t}_{m}}\} \\ & \quad \ \,=\sum\limits_{\mathbf{0}\preccurlyeq {{\mathbf{t}}^{\prime }}\preccurlyeq {{\mathbf{s}}^{\prime }}}{\sum\limits_{0\le {{t}_{m}}\le {{s}_{m}}}{\pm }}\left( \begin{matrix} {{\mathbf{s}}^{\prime }} \\ {{\mathbf{t}}^{\prime }} \\ \end{matrix} \right)\left( \begin{matrix} {{s}_{m}} \\ {{t}_{m}} \\ \end{matrix} \right){{\mathbf{z}}^{{{\mathbf{s}}^{\prime }}-{{\mathbf{t}}^{\prime }}}}z_{m}^{{{s}_{m}}-{{t}_{m}}}\{y,\mathbf{z};({{\mathbf{t}}^{\prime }},{{t}_{m}})\} \\ & \quad \ \,=\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{t}\preccurlyeq \mathbf{s}}{\pm }\left( \begin{matrix} \mathbf{s} \\ \mathbf{t} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{s}-\mathbf{t}}}\{y,\mathbf{z};\mathbf{t}\}. \\ \end{align}$

Hence, (1.1) holds in this case.

Case 2 $s_1=s_2=\cdots=s_m=0$.

In this case, we proceed by induction on $n-m$. If $n-m=1$, then

$yz_{m+1}=[y,z_{m+1}]+(-1)^{|y|}z_{m+1}y.$

Hence, (1.1) holds in this case. Assume that $n-m>1$. Put $y^{\prime}=yz_{m+1}^{s_{{m+1}}}\cdots z_{n-1}^{s_{n-1}}$ and

${\mathbf{s}}'=(\underbrace{0,0,\cdots,0}_{m\,{\rm times}},s_{m+1}, s_{m+2},\cdots,s_{n-1}).$

The induction hypothesis yields

$\begin{align} & y{{\mathbf{z}}^{\mathbf{s}}}={y}'{{z}_{n}} \\ & \quad \ \ =\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}\{y,\mathbf{z};\mathbf{{t}'}\}{{z}_{n}} \\ & \quad \ \ =\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}[\{y,\mathbf{z};\mathbf{{t}'}\},{{z}_{n}}]+\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}{{z}_{n}}\{y,\mathbf{z};\mathbf{{t}'}\} \\ & \quad \ \ =\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}\{y,\mathbf{z};(\mathbf{{t}'},1)\}+\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}{{z}_{n}}\{y,\mathbf{z};(\mathbf{{t}'},0)\} \\ & \quad \ \ =\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{t}\preccurlyeq \mathbf{s}}{\pm }\left( \begin{matrix} \mathbf{s} \\ \mathbf{t} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{s}-\mathbf{t}}}\{y,\mathbf{z};\mathbf{t}\}. \\ \end{align}$

Hence, (1.1) holds in this case.

Case 3 $(s_1,\cdots,s_m)\neq \mathbf{0}$ and $(s_{m+1},\cdots,s_n)\neq \mathbf {0}$.

Let $\mathbf{s}'=(s_1,\cdots,s_m,0,\cdots,0)$, $\mathbf{s}''=(0,\cdots,0,s_{m+1},\cdots,s_n)$. It follows from Case 1 and Case 2 that

$\begin{align} & y{{\mathbf{z}}^{\mathbf{s}}}=y{{\mathbf{z}}^{{\mathbf{{s}'}}}}{{\mathbf{z}}^{{\mathbf{{s}''}}}} \\ & \quad \ \ =\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}\{y,\mathbf{z};\mathbf{{t}'}\}{{\mathbf{z}}^{{\mathbf{{s}''}}}} \\ & \quad \ \ =\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{{t}''}\preccurlyeq \mathbf{{s}''}}{\pm }\left( \begin{matrix} {\mathbf{{s}''}} \\ {\mathbf{{t}''}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}''}-\mathbf{{t}''}}}\{\{y,\mathbf{z};\mathbf{{t}'}\},\mathbf{z};\mathbf{{t}''}\} \\ & \quad \ \ =\sum\limits_{\overset{\mathbf{0}\preccurlyeq \mathbf{{t}'}\preccurlyeq \mathbf{{s}'}}{\mathop{\mathbf{0}\preccurlyeq \mathbf{{t}''}\preccurlyeq \mathbf{{s}''}}}\,}{\pm }\left( \begin{matrix} {\mathbf{{s}'}} \\ {\mathbf{{t}'}} \\ \end{matrix} \right)\left( \begin{matrix} {\mathbf{{s}''}} \\ {\mathbf{{t}''}} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{{s}'}-\mathbf{{t}'}}}{{\mathbf{z}}^{\mathbf{{s}''}-\mathbf{{t}''}}}\{\{y,\mathbf{z};\mathbf{{t}'}\},\mathbf{z};\mathbf{{t}''}\} \\ & \quad \ \ =\sum\limits_{\mathbf{0}\preccurlyeq \mathbf{t}\preccurlyeq \mathbf{s}}{\pm }\left( \begin{matrix} \mathbf{s} \\ \mathbf{t} \\ \end{matrix} \right){{\mathbf{z}}^{\mathbf{s}-\mathbf{t}}}\{y,\mathbf{z};\mathbf{t}\}. \\ \end{align}$

Hence, (1.1) holds in this case.

In conclusion, we finish the proof by the three cases above.

We have the following super version of Engel's Theorem in Lie algebras.

Lemma 1.4 Let $V=V_{\bar{0}}\oplus V_{\bar{1}}$ be a finite-dimensional $\mathbb{Z}_2$-graded vector space and $\mathfrak{g}\subseteq\mathfrak{g}\mathfrak{l}(V)$ be a Lie super subalgebra. Moreover, assume that $\mathfrak{g}$ consists of nilpotent transformations. Then there exists a nonzero element $v\in V_{\bar{0}}\cup V_{\bar{1}}$ such that $xv=0$ for any $x\in\mathfrak{g}$.

Proof Let $m={\rm dim}\mathfrak{g}_{\bar{1}}$. We proceed by induction on m. For the case $m=0$, the assertion follows from Engel's Theorem (see [18]). Assume that $m=1$ and $\mathfrak{g}_{\bar{1}}={\rm span}_{\mathbb{F}}\{y\}$. Since $y$ is nilpotent, $W_1:=\{v\in V\mid yv=0\}$ is a nonzero $\mathbb{Z}_2$-graded subspace. Moreover, it is easy to check that $W_1$ is a $\mathfrak{g}_{\bar{0}}$-submodule. By Engel's Theorem again, $W_2:=\{v\in W_1\mid xv=0,\,\forall\,x\in\mathfrak{g}_{\bar{0}}\}$ is a nonzero $\mathbb{Z}_2$-graded subspace. Consequently, any nonzero homogeneous vector v in $W_2$ satisfies the desired requirement.

Assume that $n>1$ and the assertion holds for any $m<n$. We will show that it also holds for $m=n$. For that, regard $\mathfrak{g}_{\bar{1}}$ as a $\mathfrak{g}_{\bar{0}}$-module via adjoint action. Since

$({\rm ad} x)^{p^r}(y)=x^{p^r}y-yx^{p^r}=0,\, \forall\,x\in\mathfrak{g}_{\bar{0}},y\in\mathfrak{g}_{\bar{1}}, r>0,$

it follows that $\dim_{\mathbb{F}}[\mathfrak{g}_{\bar{0}},\mathfrak{g}_{\bar{1}}] <\dim_{\mathbb{F}}\mathfrak{g}_{\bar{1}}=n$ by applying Engel's Theorem to $\mathfrak{g}_{\bar 0}$ and its adjoint module $\mathfrak{g}_{\bar 1}$. This implies that the odd part of the derived algebra $[\mathfrak{g},\mathfrak{g}]$ has dimension strictly less than n. According to the induction hypothesis, $W_3:=\{v\in V\mid xv=0,\,\forall\,x\in [\mathfrak{g},\mathfrak{g}]\}$ is a nonzero $\mathbb{Z}_2$-graded subspace.

Let $\{x_1,\cdots,x_l\}$ be a homogeneous basis of $\mathfrak{g}$. Since $x_1$ is nilpotent, and $W_3$ is invariant under the action of $x_1$, it follows that $W_3^{x_1}:=\{v\in W_3\mid x_1v=0\}$ is a nonzero $\mathbb{Z}_2$-graded subspace. For $2\leq i\leq l$, define $W_3^{x_1,\cdots,x_i}:=\{v\in W_3^{x_1,\cdots,x_{i-1}}\mid x_iv=0\}$ inductively. These are nonzero $\mathbb{Z}_2$-graded subspaces by a similar argument. Then any nonzero homogeneous vector v in $W_3^{x_1,\cdots,x_l}$ satisfies the requirement of the assertion.

As a consequence of Lemma 1.4, we get the following preliminary result on representations of Lie superalgebras.

Lemma 1.5 Let $V=V_{\bar{0}}\oplus V_{\bar{1}}$ be a $\mathbb{Z}_2$-graded vector space and $\mathfrak{g}\subseteq L\subseteq\mathfrak{g}\mathfrak{l}(V)$ be Lie super subalgebras. Then the following statements hold.

(1) If $[\mathfrak{g},\mathfrak{g}]$ consists of nilpotent transformations and $\mathbb{F}$ contains all eigenvalues of elements in $\mathfrak{g}$, then there exists nonzero $v\in V_{\bar{0}}\cup V_{\bar{1}}$ and $\lambda\in\mathfrak{g}^*$ such that $xv=\lambda(x)v,\,\forall\,x\in\mathfrak{g}$.

(2) Let $\lambda:\,\mathfrak{g}\longrightarrow\mathbb{F}$ be an eigenvalue function, i.e., $x - \lambda (x){\rm{i}}{{\rm{d}}_V}$ is nilpotent for any $x\in\mathfrak{g}$. Suppose that $\lambda(x)=0$ for any $x\in [\mathfrak{g},\mathfrak{g}]$. Then $\lambda$ is linear.

(3) Keep assumptions as in (1). Moreover, assume that $\mathfrak{g}$ is an ideal of $L$ and V is an irreducible $L$-module. Then $[\mathfrak{g},\mathfrak{g}]=0$, and any $x\in\mathfrak{g}$ has a unique eigenvalue $\lambda(x)$ on V, and $\lambda:\,\mathfrak{g}\longrightarrow\mathbb{F}$ is linear.

Proof (1) According to Lemma 1.4,

$W_1:=\{v\in V\mid xv=0,\,\forall\,x\in [\mathfrak{g},\mathfrak{g}]\}\neq 0.$

Take any $x\in\mathfrak{g}_{\bar{1}}$ and $y, z\in\mathfrak{g}_{\bar{0}} \cup\mathfrak{g}_{\bar{1}}$, then

$[y,z] x v=[[y,z],x]v+(-1)^{|y|+|z|}x[y,z]v=0.$

Hence, $W_1$ is invariant under the action of $\mathfrak{g}_{\bar{1}}$. Moreover, since

$x^2v=\dfrac{1}{2}[x,x]v=0\;{\rm and}\;xyv=-yxv, \,\forall\,x,y\in\mathfrak{g}_{\bar{1}},v\in W_1,$

it follows that

$W_2:=\{v\in W_1\mid xv=0,\,\forall\,x\in\mathfrak{g}_{\bar{1}}\}\neq 0.$

Furthermore, $W_2$ is a $\mathfrak{g}_{\bar{0}}$-submodule with $xyw=yxw,\,\forall\,x,y\in\mathfrak{g}_{\bar{0}},w\in W_2$, so that we can find a nonzero homogeneous element v in $W_2$ and $\lambda\in\mathfrak{g}^*$ such that $xv=\lambda(x)v,\,\forall\,x\in\mathfrak{g}$.

(2) By (1), there exists $v\in V_{\bar{0}}\cup V_{\bar{1}}$ such that $xv=\lambda(x) v$. Since the left hand side is linear in x, so is the right hand side.

(3) By (1), there exists $v\in V_{\bar{0}}\cup V_{\bar{1}}$ such that $xv=0,\,\forall\,x\in [\mathfrak{g},\mathfrak{g}]$. Since V is an irreducible $L$-module, $V=U(L)v$. Consequently, $[\mathfrak{g},\mathfrak{g}]$ acts trivially on V, since $\mathfrak{g}$ is an ideal of $L$. This means that $[\mathfrak{g},\mathfrak{g}]=0$. Let $x\in\mathfrak{g}_{\bar{0}}$ and $\lambda(x)$ be an eigenvalue of x, then $[x^p,L]=({\rm ad}x)^p L\subset [\mathfrak{g},\mathfrak{g}]=0$, and $\mathcal{V}:=\{v\in V\mid x^pv=\lambda(x)^pv\}$ is a nonzero $L$-submodule. The irreducibility of V as an $L$-module implies that $\mathcal{V}$ coincides with V, i.e., $x-\lambda (x)\text{i}{{\text{d}}_{V}}$ is nilpotent. Hence, $\lambda(x)$ is the unique eigenvalue of x. On the other hand, for any $x\in\mathfrak{g}_{\bar{1}}$,

$x^2=\dfrac{1}{2}[x,x]\in [\mathfrak{g},\mathfrak{g}]=0.$

This implies that any element $x\in\mathfrak{g}_{\bar{1}}$ is nilpotent, and 0 is the unique eigenvalue. The assertion that $\lambda$ is linear follows from (2).

1.3 Restricted Lie superalgebras

The following definition is a generalization of the notion of restricted Lie algebras^{[17, 19]} to the case of Lie superalgebras.

Definition 1.6^[20] A Lie superalgebra $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ is called a restricted one if $\mathfrak{g}_{\bar{0}}$ is a restricted Lie algebra and $\mathfrak{g}_{\bar{1}}$ is a restricted $\mathfrak{g}_{\bar{0}}$, -module under the adjoint action. This is equivalent to saying that there exists a so-called p-mapping $[p]$ on $\mathfrak{g}_{\bar{0}}$ such that the following properties hold:

(ⅰ)$({\rm ad} x)^p={\rm ad}(x^{[p]}){\rm for\;all}\,\,x\in\mathfrak{g}_{\bar{0}}$;

(ⅱ)$(ax)^{[p]}=a^px^{[p]}{\rm for\;all}\;a\in {\mathbb{F}}, x\in\mathfrak{g}_{\bar{0}}$;

(ⅲ)$(x+y)^{[p]}=x^{[p]}+y^{[p]}+\sum\limits_{i=1}^{p-1}s_i(x,y) {\rm for\;all}\;x,y\in\mathfrak{g}_{\bar{0}}$, where those $s_i(x,y)\in\mathfrak{g}_{\bar{0}}$ ($1\leq i\leq p-1$) are defined via the following formula:

${\rm ad}(tx+y)^{p-1}(x)=\sum\limits_{i=1}^{p-1}is_i(x,y)t^{i-1}{\rm for\;all}\;x,y\in\mathfrak{g}_{\bar{0}}.$

Here t is an indeterminate.

Remark 1.7 Let $(\mathfrak{g},[p])$ be a restricted Lie superalgebra. Set $\xi(x):=x^p-x^{[p]}\in U(\mathfrak{g})$ for $x\in\mathfrak{g}_{\bar{0}}$. According to Definition 1.6(i), $\xi(x)\in Z(\mathfrak{g})$ for any $x\in\mathfrak{g}_{\bar{0}}$. Moreover, $\xi:\,\mathfrak{g}_{\bar{0}}\longrightarrow Z(\mathfrak{g})$ is p-semilinear, i.e., $\xi(ax+by)=a^p\xi(x)+b^p\xi(y), \,\forall\,x,y\in\mathfrak{g}_{\bar{0}},a,b\in\mathbb{F}$.

Example 1.8 Let $\mathfrak{g}=\mathfrak{g}\mathfrak{l}(m|n)$ be the general linear Lie superalgebra. Let

$\begin{align} & [p]:\quad {{\mathfrak{g}}_{{\bar{0}}}}\to {{\mathfrak{g}}_{{\bar{0}}}} \\ & \quad \quad \ x\to {{x}^{p}}, \\ \end{align}$

where $x^p=\underbrace{x\cdot x\cdot\cdots\cdot x}_{p\,{\rm times}}$. Then $(\mathfrak{g},[p])$ is a restricted Lie superalgebra. More generally, Lie superalgebras of algebraic supergroups are restricted Lie superalgebras (see ^[2]).

Proposition 1.9 Let $\mathfrak{g}$ be a restricted subalgebra of a restricted Lie superalgebra $(G,[p])$. Let $[p]':\mathfrak{g}_{\bar{0}}\longrightarrow\mathfrak{g}_{\bar{0}}$ be a mapping. Then the following statements are equivalent.

(1)$[p]'$ is a p-mapping on $\mathfrak{g}$.

(2) There exists a p-semilinear mapping $f:\mathfrak{g}_{\bar{0}}\longrightarrow {\mathfrak{z}}_{_{G_{\bar{0}}}}(\mathfrak{g})$ such that $[p]' =[p]|_{\mathfrak{g}_{\bar{0}}}+f$, where ${\mathfrak{z}}_{_{G_{\bar{0}}}}(\mathfrak{g})=\{x\in G_{\bar{0}}\mid [x,y]=0,\,\forall\,y\in\mathfrak{g}\}$.

Proof ${(1)}\Longrightarrow {(2)}$. Set

$\begin{align} & f:\quad {{\mathfrak{g}}_{{\bar{0}}}}\to {{G}_{{\bar{0}}}} \\ & \quad \quad x\to {{x}^{{{[p]}^{\prime }}}}-{{x}^{[p]}}. \\ \end{align}$

Since

$[f(x),y]=[x^{[p]'}-x^{[p]},y]=({\rm ad} x)^p(y)-({\rm ad} x)^p(y)=0,\,\forall\,x\in\mathfrak{g}_{\bar{0}},y\in\mathfrak{g},$

$f$ actually maps $\mathfrak{g}_{\bar{0}}$ into ${\mathfrak{z}}_{_{G_{\bar{0}}}}(\mathfrak{g})$. For any $x,y\in\mathfrak{g}_{\bar{0}}$ and $a,b\in\mathbb{F}$, we have

$\begin{align} & f(ax+by)={{a}^{p}}{{x}^{{{[p]}^{\prime }}}}+{{b}^{p}}{{y}^{{{[p]}^{\prime }}}}+\sum\limits_{i=1}^{p-1}{{{s}_{i}}}(ax,by)-({{a}^{p}}{{x}^{[p]}}+{{b}^{p}}{{y}^{[p]}}+\sum\limits_{i=1}^{p-1}{{{s}_{i}}}(ax,by)) \\ & \quad \quad \quad ={{a}^{p}}f(x)+{{b}^{p}}f(y). \\ \end{align}$

Consequently, $f$ is p-semilinear.

${(2)}\Longrightarrow{(1)}$. We need to show that the three conditions in Definition 1.6 hold for $[p]'$.

(ⅰ)${\rm ad}(x^{[p]'})={\rm ad}(x^{[p]}+f(x))={\rm ad}(x^{[p]})=({\rm ad} x)^p,\,\forall\,x\in\mathfrak{g}_{\bar{0}}$.

(ⅱ)$(\lambda x)^{[p]'}=(\lambda x)^{[p]}+f(\lambda x)=\lambda^p x^{[p]}+\lambda^p f(x)=\lambda^p x^{[p]'},\,\forall\,x\in\mathfrak{g}_{\bar{0}}, \lambda\in\mathbb{F}$.

(ⅲ)For any $x,y\in\mathfrak{g}_{\bar{0}}$,

$\begin{align} & {{(x+y)}^{{{[p]}^{\prime }}}}={{(x+y)}^{[p]}}+f(x+y)={{x}^{[p]}}+f(x)+{{y}^{[p]}}+f(y)+\sum\limits_{i=1}^{p-1}{{{s}_{i}}}(x,y) \\ & \quad \quad \quad \quad ={{x}^{{{[p]}^{\prime }}}}+{{y}^{{{[p]}^{\prime }}}}+\sum\limits_{i=1}^{p-1}{{{s}_{i}}}(x,y). \\ \end{align}$

The proof is completed.

Let $(\mathfrak{g},[p])$ be a finite-dimensional restricted Lie superalgebra over $\mathbb{F}$. Let $Z_0(\mathfrak{g})$ be the $\mathbb{F}$-algebra generated by ${{x}^{p}}-{{x}^{[p]}}$ for $x\in\mathfrak{g}_{\bar{0}}$. Let $I_0(\mathfrak{g})$ be the ideal in $U(\mathfrak{g})$ generated by ${{x}^{p}}-{{x}^{[p]}}$ for $x\in\mathfrak{g}_{\bar{0}}$, and $u(\mathfrak{g})=U(\mathfrak{g})/I_0(\mathfrak{g})$ which is usually called the restricted enveloping superalgebra. Suppose that $\{x_1,\cdots,x_n\}$ is a basis of $\mathfrak{g}_{\bar{0}}$, and $\{y_1,\cdots,y_m\}$ is a basis of $\mathfrak{g}_{\bar{1}}$. It follows from the semilinearity of $\xi$ that $Z_0(\mathfrak{g})$ is generated by $\xi(x_1),\cdots,\xi(x_n)$. Moreover, by PBW Theorem, we have

Proposition 1.10 Keep notations as above, then the following statements hold.

(1) The elements $\xi(x_1),\cdots,\xi(x_n)$ are algebraically independent generators for $Z_0(\mathfrak{g})$, i.e., $Z_0(\mathfrak{g})={\mathbb{F}}[\xi(x_1),\cdots,\xi(x_n)]$ is a polynomial algebra of n indeterminates.

(2) The universal enveloping superalgebra $U(\mathfrak{g})$ is free over $Z_0(\mathfrak{g})$ with basis

$\{x_1^{a_1}\cdots x_n^{a_n}y_1^{b_1}\cdots y_m^{b_m}\mid 0\leq a_i\leq p-1,b_j=0,1,1\leq i\leq n,1\leq j\leq m\}.$

(3) The restricted enveloping superalgebra $u(\mathfrak{g})$ is finite-dimensional, and has a basis

$\{\bar{x}_1^{a_1}\cdots \bar{x}_n^{a_n}\bar{y}_1^{b_1}\cdots \bar{y}_m^{b_m}\mid 0\leq a_i\leq p-1,b_j=0,1,1\leq i\leq n, 1\leq j\leq m\}.$

2 General representation theory

In this section, we always assume that $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ is a finite-dimensional Lie superalgebra over an algebraically closed field of characteristic $p>2$. We will show that each simple $\mathfrak{g}$-module is finite-dimensional, and the dimensions of simple $\mathfrak{g}$-modules have an upper bound. Moreover, each finite-dimensional Lie superalgebra can be embedded into a finite-dimensional restricted Lie superalgebra.

Proposition 2.1 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a finite-dimensional Lie superalgebra over an algebraically closed field $\mathbb{F}$ of characteristic $p>2$. Then the universal enveloping superalgebra $U(\mathfrak{g})$ is a finitely generated $Z(\mathfrak{g})$-module, and $Z(\mathfrak{g})$ is a finitely generated $\mathbb{F}$-algebra.

Proof (1) Let $\{x_1,\cdots,x_n\}$ be a basis of $\mathfrak{g}_{\bar{0}}$ and $\{y_1,\cdots,y_m\}$ be a basis of $\mathfrak{g}_{\bar{1}}$. Consider

$\{({\rm ad} x_i)^{p^j}\mid 1\leq i\leq n,j=0,1,\cdots\}$

as elements in ${\rm End}_{{\mathbb{F}}}(\mathfrak{g})$. Since $\mathfrak{g}$ is finite-dimensional, there exists $d_i\in\mathbb{N}\,(1\leq i\leq n)$ such that

$({\rm ad} x_i)^{p^{d_i}}=\sum\limits_{0\leq j<d_i} a_{ij}({\rm ad} x_i)^{p^j},\,\forall\,1\leq i\leq n.$

Consequently, $z_i:=x_i^{p^{d_i}}-\sum\limits_{0\leq j<d_i} a_{ij}x_i^{p^j}\in Z(\mathfrak{g}),1\leq i\leq n$. Let $\mathcal{O}$ be the subalgebra of $Z(\mathfrak{g})$ generated by $z_i,1\leq i\leq n$. By PBW Theorem, $\mathcal{O}$ is a polynomial algebra of n indeterminates, and as an $\mathcal{O}$-module, $U(\mathfrak{g})$ is spanned by

$\{x_1^{i_1}\cdots x_n^{i_n}y_1^{j_1}\cdots y_m^{j_m}\mid 0\leq i_k<p^{d_k},j_s=0,1,1\leq k\leq n,1\leq s\leq m\}.$

(2.1)

In particular, as a $Z(\mathfrak{g})$-module, $U(\mathfrak{g})$ is spanned by those elements in (2.1).

(2) By (1), $U(\mathfrak{g})$ is a Noetherian $\mathcal{O}$-module. Hence, as a submodule, $Z(\mathfrak{g})$ is also a Noetherian $\mathcal{O}$-module. Consequently, $Z(\mathfrak{g})$ is a finitely generated $\mathcal{O}$-module. Since $\mathcal{O}$ is finitely generated, it follows that $Z(\mathfrak{g})$ is also finitely generated.

Theorem 2.2 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a finite-dimensional Lie superalgebra over an algebraically closed field $\mathbb{F}$ of characteristic $p>2$. Then the following statements hold.

(1) Each irreducible representation of $\mathfrak{g}$ is finite-dimensional.

(2) There exists a positive integer $M(\mathfrak{g})$ such that every irreducible representation of $\mathfrak{g}$ has dimension less than $M(\mathfrak{g})$.

Proof By Proposition 2.1, we can assume that $U(\mathfrak{g})=\sum\limits_{i=1}^r Z(\mathfrak{g})u_i$. Let V be a simple $\mathfrak{g}$-module. Take a nonzero homogeneous element v in V, then

$V=U(\mathfrak{g})v=\sum\limits_{i=1}^r Z(\mathfrak{g})u_iv.$

Hence, the module V is finitely generated over $Z(\mathfrak{g})$. Since $Z(\mathfrak{g})$ is Noetherian, there exists a maximal $Z(\mathfrak{g})$-submodule $V'\subset V$. Consequently, $V/V'\cong Z(\mathfrak{g})/\mathfrak{m}$ as $Z(\mathfrak{g})$-modules for some maximal ideal $\mathfrak{m}$ of $Z(\mathfrak{g})$. Hence, $\mathfrak{m} V\subseteq V'\subsetneqq V$. Since $\mathfrak{m} V$ is a $U(\mathfrak{g})$-submodule of V and V is irreducible, it follows that $\mathfrak{m} V=0$. Therefore, $Z(\mathfrak{g})$ acts on V as $Z(\mathfrak{g})/\mathfrak{m}\cong\mathbb{F}$. Part (1) is proved. Moreover, by the discussion above, $r+1$ is an upper bound $M(\mathfrak{g})$.

Remark 2.3 When $\mathfrak{g}$ is a restricted Lie superalgebra, the results in Theorem 2.2 were asserted in ^[3].

Example 2.4 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a subalgebra of $\mathfrak{g}\mathfrak{l}(2|1)$ with $\mathfrak{g}_{\bar{0}}=\text{span}_{{\mathbb{F}}}\{h,x\}$, $\mathfrak{g}_{\bar{1}}=\text{span}_{{\mathbb{F}}}\{y\}$, where

$h=\left(\begin{array}{ccc} 1 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr \end{array}\right), x=\left(\begin{array}{ccc}0 & 1 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr \end{array}\right), y=\left(\begin{array}{ccc} 0 & 0 & 1 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr \end{array}\right).$

Note that

$[h,x]=x,\,[h,y]=y,\,[x,y]=[y,y]=0$

and

$h^{[p]}=h,\,x^{[p]}=0.$

Hence, $x^p$ and $h^p-h$ are contained in $Z(\mathfrak{g})$. Consequently,

$U(\mathfrak{g})=\sum\limits_{\stackrel{0\leq i,j<p}{0\leq k\leq 1}}Z(\mathfrak{g})h^i x^j y^k.$

It is easy to check that

$hx^i=x^i(h+i),\,\,xh^j=(h-1)^jx,\,\forall\,1\leq i,j\leq p-1.$

(2.2)

Let $M=M_{\bar{0}}\oplus M_{\bar{1}}$ be an irreducible $\mathfrak{g}$-module. By Theorem 2.2, $M$ is finite-dimensional and $x^p$ acts as a scalar on $M$, saying $a^p$. Hence, $(x-a)^p\cdot M=(x^p-a^p)\cdot M=0$.

Case 1 $a=0$.

Let $\mathfrak{g}'=\text{span}_{{\mathbb{F}}}\{x,y\}$. Then $\mathfrak{g}'$ is a subalgebra of $\mathfrak{g}$. According to Lemma 1.4, $M':= \{m\in M\mid z\cdot m=0,\,\forall\,z\in\mathfrak{g}'\}$ is a nonzero $\mathbb{Z}_2$-graded subspace. Moreover, $M'$ is a $\mathfrak{g}$-submodule of $M$, so that $M=M'$ by the irreducibility of $M$ as a $\mathfrak{g}$-module. Hence, $M$ is a simple module for the commutative Lie algebra $\mathfrak{g}/\mathfrak{g}'\cong {\mathbb{F}} h$. Therefore, $\dim_{\mathbb{F}}M=1$ and $h$ acts as a scalar on $M$, while $x,y$ act trivially. Conversely, given any scalar $b\in\mathbb{F}$, we get a one-dimensional simple $\mathfrak{g}$-module, denoted by $\mathcal{M}_b$, in which $h$ acts as multiplication by $b$, and $\mathfrak{g}'$ acts trivially.

Case 2 $a\neq 0$.

In this case, there exists $0\neq v_0\in M_{\bar{0}}\cup M_{\bar{1}}$ such that $x\cdot v_0=av_0$. Since $M$ is finite-dimensional and $h^p-h\in Z(\mathfrak{g})$, there exists $b\in\mathbb{F}$ such that

$(h^p-h)\cdot v=h^p\cdot v-h\cdot v=b^p v,\,\forall\,v\in M.$

Set $v_i:=h^i\cdot v_0$ for $1\leq i\leq p$. Then $v_p=b^pv_0+v_1$. By (2.2), for $1\leq i\leq p-1$, we have

$x\cdot v_i=(h-1)^i av_0=a\sum\limits_{j=0}^i (-1)^j{i\choose j}v_{i-j}.$

(2.3)

It follows that $M'':={\rm span}_{{\mathbb{F}}}\{v_0,v_1,\cdots, v_{p-1}\}$ is stable under x and $h$. We claim that $v_0,\cdots, v_{p-1}$ are linearly independent. Suppose the contrary, then there exists some $j<p-1$ such that $M''={\rm span}_{{\mathbb{F}}}\{v_0, v_1,\cdots,v_j\}$. It follows from (2.3) that ${\rm tr}(x|_{M''})=(j+1)a$. On the other hand, since $[h,x]=x$, we have ${\rm tr}(x|_{M''})=0$. This implies that $(j+1)a=0$, i.e., $j+1\equiv 0\,\,\,({\rm mod}p)$, a contradiction. Therefore, $v_0, v_1,\cdots,v_{p-1}$ are linearly independent. Moreover, $M''$ is an irreducible $\mathfrak{g}_{\bar{0}}$-submodule, since up to scalars, $v_0$ is the unique eigenvector of x on $M''$. We have the following natural epimorphism of $\mathfrak{g}$-modules:

$\pi:\,\,U(\mathfrak{g}) \otimes_{U(\mathfrak{g}_{\bar{0}})}M''\longrightarrow M,$

which is surjective by the simplicity of $M$ as a $\mathfrak{g}$-module. It is easy to check that $U(\mathfrak{g})\otimes_{U(\mathfrak{g}_{\bar{0}})}M''$ has a unique maximal submodule $y\otimes M''$. Consequently, $M\cong U(\mathfrak{g})\otimes_{U(\mathfrak{g}_{\bar{0}})}M''/y\otimes M''$, and $\dim_{{\mathbb{F}}}M=p$. Conversely, given $a,b\in\mathbb{F}$ with $a\neq 0$, we have a simple $\mathfrak{g}$-module $M$ of dimension p with basis $v_0,\cdots,v_{p-1}$ such that $y$ acts trivially, and the actions of $h$ and x are given as above. We denote this simple $\mathfrak{g}$-module by $\mathcal{M}_{(a,b)}$.

In conclusion, $\{\mathcal{M}_b,\mathcal{M}_{(a,b)}\mid a\in\mathbb{F}^{\times},b\in\mathbb{F}\}$ exhausts all non-isomorphic irreducible $\mathfrak{g}$-modules.

In the following, we study the connection of restricted and ordinary Lie superalgebras.

Definition 2.5 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a Lie superalgebra.

(1) A triple $(G,[p],\iota)$ consisting of a restricted Lie superalgebra $(G,[p])$ and a Lie superalgebra homomorphism $\iota:\,\mathfrak{g}\longrightarrow G$ is called a p-envelope of $\mathfrak{g}$ if $\iota$ is injective and $G=\iota(\mathfrak{g})_p$, where $\iota(\mathfrak{g})_p$ denotes the restricted subalgebra generated by $\iota(\mathfrak{g})$.

(2) A p-envelope $(G,[p],\iota)$ of $\mathfrak{g}$ is called universal, if it satisfies the following universal property: For any restricted Lie superalgebra $(H,[p]')$ and any homomorphism $f:\mathfrak{g}\longrightarrow H$, there exists a unique restricted homomorphism $g:\,(G,[p])\longrightarrow (H,[p]')$ such that $g\circ \iota= f$.

The following result asserts that the universal p-envelope of a Lie superalgebra always exists and is unique.

Proposition 2.6 Every Lie superalgebra $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ has a unique universal p-envelope $\hat{\mathfrak{g}}$.

Proof Let $\widehat{\mathfrak{g}}$ be the restricted subalgebra of $U(\mathfrak{g})$ generated by $\mathfrak{g}$. Let $H$ be a restricted Lie superalgebra and $f:\,\mathfrak{g}\longrightarrow H$ be a homomorphism. Recall that $H$ canonically embedded into $u(H)$. The universal property of $U(\mathfrak{g})$ gives rise to an associative homomorphism $\bar{f}:\,U(\mathfrak{g})\longrightarrow u(H)$ and $\mathfrak{g}\subset\bar{f}^{-1}(H)$. Let $x\in\mathfrak{g}_{\bar{0}}\subset\bar{f}^{-1}(H_{\bar{0}})$, then $\bar{f}(x)\in H_{\bar{0}}$ and $\bar{f}(x^p)=\bar{f}(x)^p=\bar{f}(x)^{[p]}\in H$. So, $x^p\in\bar{f}^{-1}(H)$. Therefore, $\bar{f}:\,\widehat{\mathfrak{g}}\longrightarrow H$ is an extension of $f$. Since $\widehat{\mathfrak{g}}$ is generated by $\mathfrak{g}$ and the p-th powers, this extension is unique. The uniqueness of $\widehat{\mathfrak{g}}$ follows from the definition of the universal p-envelope.

Proposition 2.7 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a Lie superalgebra. Then the following statements hold.

(1) If $\mathfrak{g}$ is finite-dimensional, and $(\bar{\mathfrak{g}},[p],\iota)$ is a p-envelope of $\mathfrak{g}$, then $\bar{\mathfrak{g}}/C(\bar{\mathfrak{g}})$ is finite-dimensional.

(2) If $\mathfrak{g}$ is finite-dimensional, then $\mathfrak{g}$ possesses a finite-dimensional p-envelope.

(3) Each homomorphism of Lie superalgebras $f:\,\mathfrak{g}\longrightarrow\mathfrak{h}$ can be extended to a restricted homomorphism $\widehat{f}:\,\widehat{\mathfrak{g}}\longrightarrow\widehat{\mathfrak{h}}$. Moreover, if $f$ is injective or surjective, so is $\widehat{f}$.

Proof (1) Recall that $\bar{\mathfrak{g}}=\iota(\mathfrak{g})_p$, the restricted subalgebra generated by $\iota(\mathfrak{g})$. Hence, $[\bar{\mathfrak{g}}, \bar{\mathfrak{g}}]\subset\iota(\mathfrak{g})$, and $\iota(\mathfrak{g})$ is an ideal of $\bar{\mathfrak{g}}$. Let

$\begin{align*} \varphi:\; & \bar{\mathfrak{g}}\longrightarrow {\rm Der}_ {{\mathbb{F}}}(\iota(\mathfrak{g}))\\ & x\longmapsto{\rm ad} x|_{\iota(\mathfrak{g})}. \end{align*}$

It is easy to check that ${\rm Ker} \varphi={\mathfrak{z}}_{\bar{\mathfrak{g}}}(\iota (\mathfrak{g}))={\mathfrak{z}}_{\bar{\mathfrak{g}}} (\bar{\mathfrak{g}})=C(\bar{\mathfrak{g}})$. Consequently,

${\rm dim}_{{\mathbb{F}}}\bar{\mathfrak{g}}/C(\bar{\mathfrak{g}})\leq {\rm dim}_{{\mathbb{F}}}{\rm Der}_{{\mathbb{F}}}(\iota(\mathfrak{g}))\leq{\rm dim}_{{\mathbb{F}}}{\rm End}_{{\mathbb{F}}}(\iota(\mathfrak{g})) =({\rm dim}_{{\mathbb{F}}}\mathfrak{g})^2<+\infty.$

(2) Choose a $\mathbb{Z}_2$-graded subspace $V\subset C(\widehat{\mathfrak{g}})$ such that $C(\widehat{\mathfrak{g}})=V\oplus(C(\widehat{\mathfrak{g}})\cap \mathfrak{g})$. Then by Proposition 1.9, we can endow a $[p]$-structure on $\widehat{\mathfrak{g}}/V$ which contains $\mathfrak{g}$ isomorphically. Moreover,

${\rm dim}_{{\mathbb{F}}}\widehat{\mathfrak{g}}/V={\rm dim}_{{\mathbb{F}}}\widehat{\mathfrak{g}}/C(\widehat{\mathfrak{g}})+{\rm dim}_{{\mathbb{F}}}C(\widehat{\mathfrak{g}})\cap\mathfrak{g}<+\infty.$

Then the restricted subalgebra generated by $\mathfrak{g}$ in $\widehat{\mathfrak{g}}/V$ is the desired p-envelope of $\mathfrak{g}$.

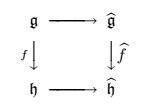
(3) Since $\mathfrak{g}\longrightarrow\mathfrak{h}\hookrightarrow\widehat{\mathfrak{h}}$, the universal property of $\widehat{\mathfrak{g}}$ yields the existence of $\widehat{f}$ such that the following diagram is commutative.

If $f$ is onto, then $\widehat{f}(\widehat{\mathfrak{g}})\supset f(\mathfrak{g})_p=\mathfrak{h}_p=\widehat{\mathfrak{h}}$, i.e., $\widehat{f}(\widehat{\mathfrak{g}})=\widehat{\mathfrak{h}}$. If $f$ is injective, it extends to an injective homomorphism $U(\mathfrak{g})\hookrightarrow U(\mathfrak{h})$. Hence, its restriction $\widehat{f}$ to $\widehat{\mathfrak{g}}$ is injective.

The following result is a superversion of Iwasawa's Theorem in the case of Lie algebras.

Theorem 2.8 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a finite-dimensional Lie superalgebra. Then $\mathfrak{g}$ admits a finite-dimensional faithful representation $\rho$. Moreover, assume $x\in\mathfrak{g}_{\bar{0}}$, then $\rho(x)$ is nilpotent if and only if ${\rm ad }x$ is nilpotent.

Proof We first assume that $\mathfrak{g}$ is restricted with the p-mapping $[p]$. Without loss of generality, according to Proposition 1.9, we can assume that $[p]|_{{\mathfrak{z}}_{\mathfrak{g}_{\bar{0}}}(\mathfrak{g})}=0$. This implies that ${\rm{ad}}x$ is nilpotent if and only if x is $[p]$-nilpotent for $x\in\mathfrak{g}_{\bar{0}}$. Let $\rho:\,\mathfrak{g}\longrightarrow \mathfrak{g}\mathfrak{l}(u(\mathfrak{g}))$ be the left multiplication in the restricted enveloping superalgebra $u(\mathfrak{g})$. Then $\rho$ is a faithful representation of $\mathfrak{g}$, and x is $[p]$-nilpotent if and only if $\rho(x)$ is nilpotnet. Consequently, ${\rm ad} x$ is nilpotent if and only if $\rho(x)$ is nilpotent.

In general, according to Proposition 2.7, there exists a finite-dimensional p-envelope of $\mathfrak{g}$, denoted by G. By the discussion above, G admits a finite-dimensional faithful representation $\varrho:\,G\longrightarrow\mathfrak{g}\mathfrak{l}(V)$ with the desired property. Since ${\rm ad}_{\mathfrak{g}}(x)$ is nilpotent if and only if ${\rm ad}_G(x)$ is nilpotent for $x\in\mathfrak{g}_{\bar{0}}$. Thus, $\rho:=\varrho|_{\mathfrak{g}}$ satisfies the required property.

We have the following close connection between representations of a Lie superalgebra and its p-envelope.

Theorem 2.9 Let G be a p-envelope of a finite-dimensional Lie superalgebra $\mathfrak{g}$ and $\rho:\,\mathfrak{g}\longrightarrow\mathfrak{g}\mathfrak{l}(V)$ be a representation of $\mathfrak{g}$. Then there exists a representation $\bar{\rho}:\,G\longrightarrow\mathfrak{g}\mathfrak{l}(V)$ extending $\rho$, and each $\mathfrak{g}$-submodule of V is a G-submodule.

Proof The statement obviously holds for $G=\widehat{\mathfrak{g}}$, the universal p-envelope of $\mathfrak{g}$. In general, by Definition 2.5, there exists an embedding $\iota:\,\mathfrak{g}\hookrightarrow G$ and a restricted homomorphism $f:\,\widehat{\mathfrak{g}}\longrightarrow G$. Then

$G=\iota(\mathfrak{g})_p=f(\mathfrak{g})_p=f(\mathfrak{g}_p) =f(\widehat{\mathfrak{g}}),$

i.e., $f$ is surjective. We can find a subspace $W$ of $\widehat{\mathfrak{g}}$ containing $\mathfrak{g}$ such that $f|_W:\,W\longrightarrow G$ is an isomorphism ($W$ is indeed a subalgebra). Then $\bar{\rho}:=\tilde{\rho}\circ f|_W^{-1}$ is the desired representation of G, where $\tilde{\rho}:\,\widehat{\mathfrak{g}}\longrightarrow\mathfrak{g}\mathfrak{l}(V)$ is the restriction of the representation $U(\mathfrak{g})\longrightarrow\mathfrak{g}\mathfrak{l}(V)$ to $\widehat{\mathfrak{g}}$.

According to Proposition 2.7, any finite-dimensional Lie superalgebra can be embedded into a finite-dimensional restricted Lie superalgebra. In the next section, we will study representations of restricted Lie superalgebras over a field of prime characteristic.

3 Representations of restricted Lie superalgebras

In this section, we always assume that the base field $\mathbb{F}$ is algebraically closed of characteristic $p>2$, and $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ is a finite-dimensional restricted Lie superalgebra over $\mathbb{F}$ with the p-mapping $[p]$.

Let $M$ be a simple $\mathfrak{g}$-module. Then $M$ is finite-dimensional by Theorem 2.2. According to Schur Lemma, $\xi (x) = {x^p} - {x^{\left[ p \right]}}$ acts on M by a scalar for any $x\in\mathfrak{g}_{\bar{0}}$. We write this scalar as ${\chi _M}{(x)^p}$ for some $\chi_{_M}(x)\in\mathbb{F}$ The semilinearity of ξ implies that $ \chi_{_M}\in\mathfrak{g}_{\bar{0}}^\ast$.

Theorem 3.1 The function $\chi_{_M}$ is called the p-character of $M$. More generally, if V is a $\mathfrak{g}$-module and $\chi\in\mathfrak{g}_{\bar{0}}^*$, then we say V has a p-character $\chi$ if

$\underbrace{x\cdots x}_{p{\rm times}}\cdot v-x^{[p]}\cdot v=\chi(x)^pv,\,\,\forall\,x\in\mathfrak{g}_{\bar{0}},v\in V.$

In the following, when we write $\chi\in\mathfrak{g}^*$, we always make convention that $\chi|_{\mathfrak{g}_{\bar{1}}}=0$. We also refer $\chi\in\mathfrak{g}_{\bar{0}}^*$ as a linear function on $\mathfrak{g}$ with $\chi(\mathfrak{g}_{\bar{1}})=0$.

Remark 3.2 If $M$ has a p-character $\chi$ and $M'$ has a p-character $\chi'$, then $M^*$ has a p-character $-\chi$ and $M\otimes M'$ has a p-character $\chi+\chi'$.

The $\mathfrak{g}$-modules with p-character $0$ are called restricted modules. They correspond to Lie superalgebra homomorphisms $\rho:\,\mathfrak{g}\longrightarrow \mathfrak{g}\mathfrak{l}(V)$ with $\rho(x)^p=\rho(x^{[p]}),\,\forall\,x\in\mathfrak{g}_{\bar{0}}$.

For $\chi\in\mathfrak{g}_{\bar{0}}^*$, define $U_{\chi}(\mathfrak{g})=U(\mathfrak{g})/(x^p-x^{[p]}-\chi(x)^p\mid x\in\mathfrak{g}_{\bar{0}})$, where $(x^p-x^{[p]}-\chi(x)^p\mid x\in\mathfrak{g}_{\bar{0}})$ denotes the ideal of $U(\mathfrak{g})$ generated by $x^p-x^{[p]}-\chi(x)^p$ for $x\in\mathfrak{g}_{\bar{0}}$. Each $U_{\chi}(\mathfrak{g})$ is called a $\chi$-reduced enveloping superalgebra of $\mathfrak{g}$. For $\chi=0$, $U_0(\mathfrak{g})$ is just the restricted enveloping superalgebra $u(\mathfrak{g})$. We have a one-to-one correspondence between $\mathfrak{g}$-modules with p-character $\chi$ and $U_{\chi}(\mathfrak{g})$-modules. By PBW Theorem, we have

Proposition 3.3 Let $\chi\in\mathfrak{g}_{\bar{0}}^*$. If $\{x_1,\cdots,x_n\}$ is a basis of $\mathfrak{g}_{\bar{0}}$ and $\{y_1,\cdots,y_m\}$ is a basis of $\mathfrak{g}_{\bar{1}}$, then the superalgebra $U_{\chi}(\mathfrak{g})$ has the following basis

$\{\bar{x}_1^{a_1}\cdots \bar{x}_n^{a_n}\bar{y}_1^ {b_1}\cdots \bar{y}_m^{b_m}\mid 0\leq a_i<p,b_j=0,1, 1\leq i\leq n,1\leq j\leq m\}.$

In particular, ${\rm dim}_{{\mathbb{F}}} U_{\chi}(\mathfrak{g})=2^{{\rm dim}_{{\mathbb{F}}}\mathfrak{g}_{\bar{1}}}p^{{\rm dim}_{\mathbb{F}}\mathfrak{g}_{\bar{0}}}$.

The following result asserts that the composition factors of a finite-dimensional indecomposable $\mathfrak{g}$-module have the same p-character.

Proposition 3.4 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a finite-dimensional restricted Lie superalgebra over an algebraically closed field $\mathbb{F}$, and $M$ a finite-dimensional indecomposable $\mathfrak{g}$-module. Then there exists a unique $\chi\in\mathfrak{g}_{\bar{0}}^*$ such that each simple composition factor of $M$ has the p-character $\chi$.

Proof Let $d={\rm dim}_{{\mathbb{F}}}M$. Take a basis $\{x_1,\cdots,x_n\}$ of $\mathfrak{g}_{\bar{0}}$. Consider $x_1^p - x_1^{[p]}$ as a linear transformation on $M$. We can decompose M as a direct sum of $\mathbb{Z}_2$-graded vector subspaces:

$M=M_{\lambda_{11}}\oplus M_{\lambda_{12}}\oplus\cdots \oplus M_{\lambda_{1s}},$

where

$M_{\lambda_{1i}}=\{v\in M| (x_1^p-x_1^{[p]}-\lambda_{1i})^dv=0\},\,\,1\leq i\leq s.$

Since $x_1^p-x_1^{[p]}\in Z(\mathfrak{g})$, each $M_{\lambda_{1i}}$ is a $\mathfrak{g}$-submodule. The indecomposability of $M$ as a $\mathfrak{g}$-module implies that $s=1$, i.e., $(x_1^p-x_1^{[p]}-\lambda_{11})^dv=0,\,\forall\,v\in M.$

Applying similar arguments, there exist unique $\lambda_{21},\cdots, \lambda_{n1}\in\mathbb{F}$ such that

$(x_i^p-x_i^{[p]}-\lambda_{i1})^dv=0,\,\forall\,i \,(2\leq i\leq n),\,v\in M.$

Let $\chi\in\mathfrak{g}_{\bar{0}}^*$ with $\chi(x_i)^p=\lambda_{i1}$ for $1\leq i\leq n$. Then

$(x^p-x^{[p]}-\chi(x)^p)^dv=0,\,\forall\,x\in\mathfrak{g}_{\bar{0}},\,v\in M.$

Consequently, each simple composition factor of $M$ admits the p-character $\chi$.

As a direct consequence, we have

Corollary 3.5 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a finite-dimensional restricted Lie superalgebra over an algebraically closed field, and V a finite-dimensional $\mathfrak{g}$-module. Then V can be decomposed into direct sum of submodules: $V=\bigoplus\limits_{i=1}^t V_i$, where the composition factors of each $V_i$ have the same p-character $\chi_i\in\mathfrak{g}_{\bar{0}}^*$ for $1\leq i\leq t$. Those $\chi_i$ ($1\leq i\leq t$) are called the generalized p-characters of V.

In the following, we always assume that $I$ is an ideal of a finite-dimensional restricted Lie superalgebra $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$, and $\lambda\in I_{\bar{0}}^*$ with $\lambda([I,I])=0$. Let

$\mathfrak{g}^{\lambda}:=\{x\in\mathfrak{g}\mid\lambda([x,y])=0,\,\forall\,y\in I\},$

which is a restricted subalgebra of $\mathfrak{g}$. Moreover, $I$ is also an ideal of $\mathfrak{g}^{\lambda}$.

Let $\{z_1,\cdots,z_l,z_{l+1},\cdots,z_r\}$ be a cobasis of $\mathfrak{g}^{\lambda}$ in $\mathfrak{g}$, where $z_i\in\mathfrak{g}_{\bar{0}}$, $z_j\in\mathfrak{g}_{\bar{1}}$ for $1\leq i\leq l< j\leq r$. For a given $\chi\in\mathfrak{g}^*$ (recall the convention that $\chi|_{\mathfrak{g}_{\bar{1}}}=0$) and a finite-dimensional $\mathfrak{g}^{\lambda}$-module $M$ with the p-character $\chi|_{\mathfrak{g}^{\lambda}}$ and

$x\cdot v=\lambda(x)v,\,\forall\,x\in I,\,v\in M,$

let

$V:={\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}} (M,\chi)=U_{\chi}(\mathfrak{g})\otimes_{U_{\chi}(\mathfrak{g}^{\lambda})}M$

be the induced $U_{\chi}(\mathfrak{g})$-module. As a vector space, we have

$V=\sum\limits_{\textbf{0}\preccurlyeq \mathbf{s}\preccurlyeq\tau}{\mathbb{F}}\mathbf{z}^{\mathbf{s}}\otimes M,$

where $\mathbf{z}^{\mathbf{s}}=z_1^{s_1}\cdots z_r^{s_r}$ for $\mathbf{s}=(s_1,\cdots,s_r)\in{\mathbb{N}}^r$ and

$\tau=(\underbrace{p-1,\cdots,p-1}_{l\,{\rm times}}, \underbrace{1,\cdots,1}_{r-l\,{\rm times}}).$

For $j\in\mathbb{N}$, set

$V_{(j)}=\sum\limits_{\stackrel{\textbf{0} \preccurlyeq\mathbf{s}\preccurlyeq\tau}{|\mathbf{s}|\leq j}}{\mathbb{F}}\mathbf{z}^{\mathbf{s}}\otimes M.$

We then have a filtration

$0\subset V_{(0)}\subset V_{(1)}\subset\cdots \subset V_{((p-2)l+r)}=V.$

We need the following lemma for later use.

Lemma 3.6 Keep notations as above.

(1) There exist $y_1,\cdots,y_l\in I_{\bar{0}}$ and $y_{l+1},\cdots,y_r\in I_{\bar{1}}$ such that $\lambda([y_i, z_j])=\delta_{ij}$ for $1\leq i,j\leq r$.

(2) For any $v\in M$, $\mathbf{s}\in {\mathbb{N}}^r$ with $\mathbf{s}\preccurlyeq\tau$, we have

$(y_i-\lambda(y_i))\cdot \mathbf{z}^{\mathbf{s}}\otimes v\equiv \pm s_i\mathbf{z}^{\mathbf{s}-\varepsilon_i}\otimes v\,\,\,({\rm mod} \,V_{|\mathbf{s}|-2}).$

Proof (1) Set $C=\sum\limits_{i=1}^r {\mathbb{F}}z_i$. Define $B_{\lambda}(z,y)=\lambda([z,y])$ for $z\in\mathfrak{g}$ and $y\in I$. We then get a linear map

$\begin{align*} \phi:\; & C\longrightarrow I^*\\ & x\longmapsto B_{\lambda}(x,-). \end{align*}$

Then $\phi$ is injective. Consequently, $\phi(z_1),\cdots,\phi(z_r)$ are linearly independent. Hence, there exists $y_1,\cdots ,y_r\in I$ such that

$\phi(z_i)(y_j)=\lambda([z_i,y_j])=\delta_{ij},\,1\leq i,j\leq r.$

Since $\lambda(\mathfrak{g}_{\bar{1}})=0$, we can choose $y_{_{1}},\cdots,y_{_{l}}\in I_{\bar{0}}$ and $y_{_{l+1}},\cdots, y_r\in I_{\bar{1}}$.

(2) According to Lemma 1.3,

$(y_i-\lambda(y_i))\mathbf{z}^{\mathbf{s}}=\sum\limits_{\textbf{0} \preccurlyeq\mathbf{t}\preccurlyeq\mathbf{s}}\pm {\mathbf{s}\choose\mathbf{t}}\mathbf{z}^{\mathbf{s} -\mathbf{t}}\{y_i-\lambda(y_i),\mathbf{z};\mathbf{t}\}.$

For $\mathbf{t}\neq \mathbf{0}$, we have $\{y_i-\lambda(y_i),\mathbf{z};\mathbf{t}\}=\{y_i,\mathbf{z};\mathbf{t}\}\in I$, and $\{y_i,\mathbf{z};\mathbf{t}\}\otimes v\in 1\otimes M=V_{(0)}.$ Consequently,

$\begin{align*} (y_i-\lambda(y_i))\cdot\mathbf{z}^{\mathbf{s}}\otimes v & \equiv\sum\limits_{|\mathbf{t}|\leq 1}\pm {\mathbf{s}\choose \mathbf{t}}\mathbf{z}^{\mathbf{s}-\mathbf{t}} \{y_i-\lambda(y_i),\mathbf{z};\mathbf{t}\}\otimes v\\ & \equiv \pm \mathbf{z}^{\mathbf{s}}(y_i-\lambda(y_i))\otimes v\pm \sum\limits_{j=1}^r s_j\mathbf{z}^{\mathbf{s}-\varepsilon_j}[y_i, z_j] \otimes v\\ & \equiv\pm s_i\mathbf{z}^{\mathbf{s}-\varepsilon_i}\otimes v\,({\rm mod} V_{|\mathbf{s}|-2}). \end{align*}$

With aid of Lemma 3.6, we get the following result describing the submodule structure of the induced module ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi)$.

Proposition 3.7 Let $W$ be a $\mathfrak{g}$-submodule of ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi)$. Then there exists a $\mathfrak{g}^{\lambda}$-submodule $M'$ of $M$ such that $W\cap (1\otimes M)=1\otimes M'$ and $W={\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M',\chi)$.

Proof Let $M':=\{v\in M\mid 1\otimes v\in W\}$. Then $M'$ is a $\mathfrak{g}^{\lambda}$-submodule of $M$. Moreover, $W\cap (1\otimes M)=1\otimes M'$. For $j\in\mathbb{N}$, set

$W_{(j)}:=\sum\limits_{\stackrel{\mathbf{0}\preccurlyeq \mathbf{s}\preccurlyeq \tau}{|\mathbf{s}|\leq j}}{\mathbb{F}}\mathbf{z}^{\mathbf{s}}\otimes M' \subset{\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi).$

Then $W_{(0)}=W\cap V_{(0)}$. We will show that $W\cap V_{(j)}\subseteq W_{(j)}$ by induction on j. Let $j\geq 1$ and suppose that $W\cap V_{(j-1)} \subseteq W_{(j-1)}$. Let $v\in W\cap V_{(j)}$. Choose a cobasis $\{v_1,\cdots,v_t\}$ of $M'$ in $M$. Without loss of generality, we can assume that

$v=\sum\limits_{k=1}^t\sum\limits_{\stackrel{\mathbf{s} \preccurlyeq\tau}{|\mathbf{s}|\leq j}}a_{\mathbf{s},k}\mathbf{z}^{\mathbf{s}}\otimes v_k,$

where $a_{\mathbf{s},k}\in{\mathbb{F}}$ for $\mathbf{s}\preccurlyeq\tau, |\mathbf{s}|\leq j$ and $1\leq k\leq t$. According to Lemma 3.6, we have

$(y_i-\lambda(y_i))\cdot v=\sum\limits_{k=1}^t\sum\limits_{|\mathbf{s}|=j}a_{\mathbf{s}, k}s_i\mathbf{z}^{\mathbf{s}-\varepsilon_i}\otimes v_k \,\,\,({\rm mod} \,V_{(j-2)}),\,1\leq i\leq r.$

Hence, $(y_i-\lambda(y_i))\cdot v\in W\cap V_{(j-1)}\subset W_{(j-1)}$. It follows from the definition of $W_{(j-1)}$ that $s_i a_{\mathbf{s},k}=0$ for $|\mathbf{s}|=j$ and $1\leq i\leq r,1\leq k\leq t$. Consequently, $v=0$. This implies that $W\cap V_{(j)}\subseteq W_{(j)}$. On the other hand, it is obvious that $W_{(j)}\subseteq W\cap V_{(j)}$, so that $W\cap V_{(j)}=W_{(j)}, \,\forall\,j\geq 0$. Hence, $W=W\cap V=W\cap V_{(p-2)l+r}=W_{(p-2)l+r}={\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M',\chi)$.

As a direct consequence, we have the following criterion on irreducibility of the induced module ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi)$.

Theorem 3.8 The induced $U_{\chi}(\mathfrak{g})$-module ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi)$ is irreducible if and only if $M$ is irreducible.

Proof The sufficient implication is obvious. It suffices to show the necessary implication. Suppose that $M$ is irreducible. Let $W$ be a $\mathfrak{g}$-submodule of ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi)$. By Proposition 3.7, there exists a $\mathfrak{g}^{\lambda}$-submodule $M'$ of $M$ such that $W={\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M',\chi)$. Consequently, $W=0$ or ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi)$ corresponding to $M'=0$ or $M'=M$.

For a $\mathfrak{g}$-module V, set $V^{\lambda}:=\{v\in V\mid y\cdot v=\lambda(y)v,\,\forall\,y\in I\}$, which is a $\mathfrak{g}^{\lambda}$-submodule of V by a straightforward computation.

Theorem 3.9 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a finite-dimensional restricted Lie superalgebra over an algebraically closed field. Let V be an irreducible $\mathfrak{g}$-module, and $I$ be an ideal of $\mathfrak{g}$. Then the following statements hold.

(1) If V has a p-character $\chi\in\mathfrak{g}^*$ and there is $\lambda\in I^*$ with $\lambda([I,I])=0$ and $V^{\lambda}\neq 0$, then $V\cong{\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(V^{\lambda},\chi)$ and $V^{\lambda}$ is an irreducible $\mathfrak{g}^{\lambda}$-module.

(2) If $[I,I]$ operates nilpotently on V, then there exists $\chi\in\mathfrak{g}^*$, $\lambda\in I^*$ with $\lambda([I,I])=0$ such that $V\cong {\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(V^{\lambda},\chi)$.

Proof (1) Since V is irreducible, there exists $\chi\in\mathfrak{g}^*$ such that V is a finite-dimensional $U_{\chi}(\mathfrak{g})$-module, and we have the following surjective homomorphism

$\begin{align*} \Psi:\,{\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}} (V^{\lambda},\chi)&\longrightarrow V\\ u\otimes v&\longmapsto u\cdot v. \end{align*}$

Note that ${\rm Ker}\Psi$ is a $\mathfrak{g}$-submodule of ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(V^{\lambda},\chi)$ which intersects $1\otimes V^{\lambda}$ trivially. This implies that ${\rm Ker}\Psi=0$ by Proposition 3.7. Hence, $\Psi$ is an isomorphism and $V^{\lambda}$ is irreducible by Theorem 3.8.

(2) follows from Lemma 1.5 and the statement (1).

Remark 3.10 If $I\triangleleft\mathfrak{g}$ is an abelian ideal, then Theorem 3.9(2) applies.

Definition 3.11 Let V be a $\mathfrak{g}$-module and $I\triangleleft\mathfrak{g}$ be an ideal. We say $\lambda\in I^*$ a good eigenvalue function for V if $\lambda([I,I])=0$ and $V^{\lambda}\neq 0$.

Let $\chi\in\mathfrak{g}^*$ and $I\triangleleft\mathfrak{g}$. Let $\lambda\in I^*$ with $\lambda([I,I])=0$. We denote by $\mathfrak{C}_{\chi,\lambda}$ (resp. $\mathfrak{D}_{\chi,\lambda}$) the set of isomorphism classes of irreducible $\mathfrak{g}$ (resp. $\mathfrak{g}^{\lambda}$) modules with p-character $\chi$ (resp. $\chi|_{\mathfrak{g}^{\lambda}}$) and a good eigenvalue function $\lambda$.

Theorem 3.12 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be a finite-dimensional restricted Lie superalgebra over an algebraically closed field. Let $\chi\in\mathfrak{g}^*$. Let $I\triangleleft\mathfrak{g}$ be an ideal and $\lambda\in I^*$ with $\lambda([I,I])=0$. Then the following map

$\begin{align*} \Upsilon: \mathfrak{C}_{\chi,\lambda}&\longrightarrow \mathfrak{D}_{\chi,\lambda}\\ V&\longmapsto V^{\lambda} \end{align*}$

is bijective.

Proof By Theorem 3.9, $\Upsilon$ is well-defined. Let

$\begin{align*} \Gamma: \,\mathfrak{D}_{\chi,\lambda}&\longrightarrow \mathfrak{C}_{\chi,\lambda}\\ M & \longmapsto {\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi) \end{align*}$

which is well-defined by Theorem 3.8.

Let $M$ be an irreducible $\mathfrak{g}^{\lambda}$-module with p-character $\chi|_{\mathfrak{g}^{\lambda}}$ and a good eigenvalue function $\lambda$. Set $V:={\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(M,\chi)$. Then V is irreducible by Theorem 3.8. Moreover, $1\otimes M\subseteq V^{\lambda}$ by Lemma 1.5(3). Thanks to Theorem 3.9, $V\cong {\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(V^{\lambda},\chi)$. Consequently, $V^{\lambda}=1\otimes M$ by comparing their dimensions, i.e., $\Upsilon\circ\Gamma(M)\cong M$.

Conversely, let V be an irreducible $\mathfrak{g}$-module with p-character $\chi$ and a good eigenvalue function $\lambda$. Then $V\cong{\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}(V^{\lambda},\chi)$ by Theorem 3.9, i.e., $\Gamma\circ\Upsilon(V)\cong V$. Therefore, $\Upsilon$ is bijective, and $\Gamma$ is its inverse map.

Example 3.13 Let $\mathfrak{g}=\mathfrak{g}_{\bar{0}}\oplus\mathfrak{g}_{\bar{1}}$ be the so-called Heisenberg Lie superalgebra with $\mathfrak{g}_{\bar{0}}={\rm span}_{{\mathbb{F}}}\{c\}$, $\mathfrak{g}_{\bar{1}}={\rm span}_{{\mathbb{F}}}\{x_i,y_j\mid 1\leq i,j\leq n\}$, and the p-mapping $[p]$ and the Lie bracket subject to the following rules:

$c^{[p]}=c,\,[x_i,y_j]=\delta_{ij}c,\,[x_i,x_j]=[y_i,y_j]=[c, x_i]=[c,y_j]=0,\,\forall\,1\leq i,j\leq n.$

Let $0\neq \chi\in\mathfrak{g}_{\bar{0}}^*$ and $\Lambda_{\chi}:=\{\mu\in{\mathbb{F}}\mid \mu^p-\mu=\chi(c)^p\}$. Let $I={\rm span}_{{\mathbb{F}}}\{c,x_i\mid 1\leq i\leq n\}$ which is an abelian ideal of $\mathfrak{g}$. Let $\lambda\in I^*$ with $\lambda(c)\in \Lambda_{\chi}$, and $\lambda(x_i)=0,\,1\leq i\leq n$. Then $\mathfrak{g}^{\lambda}=I$ by a direct computation. By Theorem 3.8 and Theorem 3.9, each simple $\mathfrak{g}$-module with p-character $\chi$ and a good eigenvalue function $\lambda$ is of the form ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}({\mathbb{F}}v_{\lambda},\chi)$, where ${\mathbb{F}}v_{\lambda}$ is the one-dimensional $I$-module with $c\cdot v_{\lambda} =\lambda(c) v_{\lambda}$ and $x_i\cdot v_{\lambda}=0$, $1\leq i\leq n$. Moreover, for any $\chi\in\mathfrak{g}^*$, since $U_{\chi}(I)$ is a local superalgebra, any simple $U_{\chi}(I)$-module is one-dimensional, and there are totally p simple modules ${\mathbb{F}}v_{\lambda}$ with $c\cdot v_{\lambda} =\lambda v_{\lambda}$ and $x_i\cdot v_{\lambda}=0$ ($1\leq i\leq n$), where $\lambda\in\Lambda_{\chi}$. Hence, each simple $U_{\chi}(\mathfrak{g})$-module is of the form ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}({\mathbb{F}}v_{\lambda}, \chi)$ with $\lambda\in \Lambda_{\chi}$. Moreover, ${\rm Ind}_{\mathfrak{g}^{\lambda}}^{\mathfrak{g}}({\mathbb{F}}v_{\lambda}, \chi)\cong {\rm Ind}_{\mathfrak{g}^{\mu}}^{\mathfrak{g} }({\mathbb{F}}v_{\mu},\chi)$ if and only if $\lambda=\mu$.