亚式期权是一种强路径依赖型期权, 在期权到期日的收益依赖于在整个期权有效期内标的资产所经历的价格平均值, 因此亚式期权广受欢迎. Kemna和Vorst[1]通过波动率的变化求出了几何平均亚式期权定价的解析公式; Wong和Cheung[2]研究了随机波动率模型下的亚式期权定价模型; Ching-Sung Chou[3]推出了跳-扩散过程下的亚式期权定价模型.
经典的期权定价模型都假设金融资产价格(如股价)服从几何布朗运动, 但大量的实证研究结果表明, 金融资产价格并不服从几何布朗运动, 而是呈现出一种"尖峰厚尾"的分布, 且存在自相似性和长期相关性; 分数布朗运动正好具备这些性质, 能够更好地刻画金融资产价格的演化过程.但是分数布朗运动既不是Markov过程, 又不是半鞅, 所以不能使用通常的Itô积分来计算, 这给分数布朗运动下的期权定价研究带来了一定的困难.于是Cheridito[4-5]建议使用混合分数布朗运动作为噪声来驱动一个金融资产的价格, 这种噪声有着与半鞅类似的性质. Kuznetsov[6]、Zähle[7]和Mishura[8]建立了混合分数布朗运动下的Black-Scholes定价模型.王晓天[9-10]研究了分数布朗运动下带交易费用的Black-Scholes模型的欧式期权定价以及分数布朗运动下带交易费用的有波动率微笑的欧式期权定价问题.大部分对奇异期权的研究都假设标的资产满足连续扩散过程, 然而在实际金融市场中股票价格可能会出现"跳跃", 不少学者考虑用Poisson过程和布朗运动驱动的随机微分方程来描述股票价格变化并且给出了一些期权价格的解析解. Farshid Mehrdoust等[11]给出了算术平均亚式期权在带跳的双因素随机波动率模型下的数值解; Nisha Rambeerich[12]给出了当标的资产服从跳-扩散过程的欧式期权和美式期权的数值解.近年来, 不少学者在对期权进行定价时将以上两种情况同时考虑进去.肖伟林[13]运用等价鞅测度方法求解出在分数跳-扩散过程下欧式货币期权的解析解; 彭斌[14]利用分数跳-扩散过程的Itô公式给出了几何平均亚式期权定价公式并使用控制变量的方法对算术平均亚式期权进行蒙特卡罗模拟.丰月姣[15]和孙玉东[16]等利用分数跳-扩散过程的Itô公式研究了带跳的混合分数布朗运动下的利差期权定价问题. FoadShokrollahi[17]运用保险精算法得到混合分数跳-扩散过程下的利差期权定价公式.
本文假定股票价格遵循混合分数跳-扩散过程, 利用混合分数跳-扩散过程随机分析理论, 得到了混合分数-跳扩散环境下几何平均亚式期权价格所满足的Black-Scholes偏微分方程, 并通过求解该偏微分方程, 给出了几何平均亚式期权的定价公式.
1 定价模型考虑一个股票价格既有连续又有间断的复杂的金融市场, 对于连续部分有"尖峰厚尾"和"长期相关性"的特性, 对于间断部分在价格过程中有异常波动.假设交易不需要支付交易费用, 那么价格过程可由以上两个部分叠加组成, 可写成如下形式
| $\begin{align} {\rm d}S_t =(\mu _t -q_t )S_t {\rm d}t+\sigma S_t ({\rm d}M_t +{\rm d}N_t ),\end{align}$ | (1) |
其中常数
定理1 (混合分数跳-扩散过程Itô公式)假设
| $\begin{align} f(t,W_t )=&f(0,0)+\int_0^t {\frac{\partial f}{\partial x}(\tau ,W_\tau ){\rm d}W_\tau } \\[2mm] &+\int_0^t {\Big[{\dfrac{\partial f}{\partial \tau }(\tau ,W_\tau )+\dfrac{1}{2}(1+\lambda +2H\tau ^{2H-1})\dfrac{\partial ^2f}{\partial x^2}(\tau ,W_\tau )} \Big]} {\rm d}\tau . \end{align}$ | (2) |
证明 设
| $\begin{align*} f(t_1 ,W_{t_1^- } )=f(0,0)+\int_0^{t_1 } \\ {\Big[{\dfrac{\partial f}{\partial \tau }+\dfrac{1}{2}(1+2H\tau ^{2H-1})\dfrac{\partial ^2f}{\partial x^2}-\lambda \dfrac{\partial f}{\partial x}} \Big]{\rm d}\tau } +\int_0^{t_1 } {\dfrac{\partial f}{\partial x}{\rm d}B_\tau } +\int_0^{t_1 } {\dfrac{\partial f}{\partial x}{\rm d}B_\tau ^H } ,\\[2mm] f(t,W_t)=f(t_1 ,W_{t_{1} } )+\int_{t_1 }^t \\ {\Big[{\dfrac{\partial f}{\partial \tau }+\dfrac{1}{2}(1+2H\tau ^{2H-1})\dfrac{\partial ^2f}{\partial x^2}-\lambda \dfrac{\partial f}{\partial x}} \Big]{\rm d}\tau } +\int_{t_1 }^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau } +\int_{t_1 }^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau ^H } . \end{align*}$ |
因
| $\begin{align*} f(t,W_t )=&f(0,0)+\int_0^t {\Big[{\dfrac{\partial f}{\partial \tau }+\dfrac{1}{2}(1+2H\tau ^{2H-1})\dfrac{\partial ^2f}{\partial x^2}-\lambda \dfrac{\partial f}{\partial x}} \Big]{\rm d}\tau } \\[2mm] &+\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau } +\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau ^H } +f(t_{1} ,W_{t_{1} } )-f(t_{1} ,W_{t_1^- } ). \end{align*}$ |
当跳跃次数
| $\begin{align*} f(t,W_t )=&f(0,0)+\int_0^t {\Big[{\dfrac{\partial f}{\partial \tau }+\dfrac{1}{2}(1+2H\tau ^{2H-1})\dfrac{\partial ^2f}{\partial x^2}-\lambda \dfrac{\partial f}{\partial x}} \Big]{\rm d}\tau } \\[2mm] &+\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau } +\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau ^H } +\sum\limits_{\tau \le t} {f(\tau ,W_\tau )-f(\tau ,W_{\tau ^-} )} . \end{align*}$ |
设
| $\begin{align*} \sum\limits_{\tau \le t} {\Big[{g(Q_\tau )-g(Q_{\tau ^-} )} \Big]} =\int_0^t {{g}'(Q_\tau ){\rm d}Q_\tau } +\dfrac{\lambda }{2}\int_0^t {{g}"(Q_\tau ){\rm d}\tau } . \end{align*}$ |
又
| $\begin{align*} \sum\limits_{\tau \le t} {\Big[{f(\tau ,W_\tau )-f(\tau ,W_{\tau ^-} )} \Big]} =\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}Q_\tau } +\dfrac{\lambda }{2}\int_0^t {\dfrac{\partial ^2f}{\partial x^2}{\rm d}\tau }. \end{align*}$ |
那么
| $\begin{align*} f(t,W_t )=&f(0,0)+\int_0^t {\Big[{\dfrac{\partial f}{\partial \tau }+\dfrac{1}{2}(1+2H\tau ^{2H-1})\dfrac{\partial ^2f}{\partial x^2}-\lambda \dfrac{\partial f}{\partial x}} \Big]{\rm d}\tau } \\[2mm] &+\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau } +\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}B_\tau ^H } +\int_0^t {\dfrac{\partial f}{\partial x}{\rm d}Q_\tau +\dfrac{\lambda }{2}} \int_0^t {\dfrac{\partial ^2f}{\partial x^2}{\rm d}\tau } \\[2mm] =&f(0,0)+\int_0^t {\Big[{\dfrac{\partial f}{\partial \tau }+\dfrac{1}{2}(1+\lambda +2H\tau ^{2H-1})\dfrac{\partial ^2f}{\partial x^2}-\lambda \dfrac{\partial f}{\partial x}} \Big]{\rm d}\tau } +\\ \int_0^t {\dfrac{\partial f}{\partial x}{\rm d}W_\tau } _{.} \end{align*}$ |
定理2 随机微分方程(1) 的解是
| $\begin{align} S_t =S_0 \exp \Big\{ {\int_0^t {(\mu _\tau -q_\tau ){\rm d}\tau } -\dfrac{\sigma ^2}{2}(t^{2H}+\lambda t+t)+\sigma W_t } \Big\}. \end{align}$ | (3) |
证明 令
定理3 假设标的资产价格
| $\begin{align} \dfrac{\partial V}{\partial t}+(r_t -q_t )S_t \dfrac{\partial V}{\partial S_t }+\dfrac{{1}}{2}\widehat {\sigma }^{2}S_t ^2\dfrac{\partial ^2V}{\partial S_t ^2}+\dfrac{J_t (\ln S_t -\ln J_t )}{t}\cdot\dfrac{\partial V}{\partial J_t }=r_t V_t,\end{align}$ | (4) |
其中
| $\begin{align*} V_c (T,J_T ,S_T )=(J_T -K)^+. \end{align*}$ |
证明 因为亚式期权是路径依赖型期权, 几何平均亚式看涨期权在
| $\begin{align*} {\rm d}J_t =J_t \Big( {-\dfrac{1}{t^2}\int_0^t {\ln S_\tau {\rm d}\tau } +\dfrac{1}{t}\ln S_t } \Big)=J_t \dfrac{\ln S_t -\ln J_t }{t}. \end{align*}$ |
假设在金融市场中有一种债券和一种股票, 债券和股票的价格分别满足下列微分方程:
| $\begin{align*} &{\rm d}P_t =r_t P_t {\rm d}t,\\[2mm] &{\rm d}S_t =(\mu _t -q_t )S_t {\rm d}t+\sigma S_t ({\rm d}B_t +{\rm d}B_t^H +{\rm d}N_t ),\end{align*}$ |
对自融资投资策略
| $\begin{align*} {\rm d}V_t =\theta _{t}^0 {\rm d}P_t +\theta _t^1 {\rm d}S_t +\theta _t^1 q_t S_t {\rm d}t,\end{align*}$ |
由自融资交易策略, 有
| $\begin{align*} {\rm d}V_t &=\theta _{t }^0 {\rm d}P_t +\theta _t^1 {\rm d}S_t +\theta _t^1 q_t S_t {\rm d}t \\[2mm] &=(V_t -\theta _{t }^1 S_t )r_t {\rm d}t+\theta _t^1 (\mu _t -q_t )S_t {\rm d}t+\theta _t^1 \sigma S_t {\rm d}W_t +\theta _t^1 q_t S_t {\rm d}t \\[2mm] &=(V_t -\theta _{t }^1 S_t )r_t {\rm d}t+\theta _t^1 \mu _t S_t {\rm d}t+\theta _t^1 \sigma S_t {\rm d}W_t . \end{align*}$ |
由定理1和定理2, 有
| $\begin{align*} {\rm d}V_t =&\Big[{\dfrac{\partial V}{\partial t}+(\mu _t -q_t )S_t \dfrac{\partial V}{\partial S_t }+\dfrac{\ln S_t -\ln J_t }{t}J_t \dfrac{\partial V}{\partial J_t }} \Big]{\rm d}t \\[2mm] &+\dfrac{1}{2}\sigma ^2S_t ^2(1+2Ht^{2H-1}+\lambda )\dfrac{\partial ^2V}{\partial S_t ^2}{\rm d}t+\sigma S_t \dfrac{\partial V}{\partial S_t }{\rm d}W_t. \end{align*}$ |
由于期权的价值与构造的投资组合的价值相等, 故
| $\begin{align*} \theta_{t}^1 =\dfrac{\partial V}{\partial S_t },\end{align*}$ |
那么
| $\begin{array}{l} \;\;{\mu _t}{S_t}\frac{{\partial V}}{{\partial {S_t}}}{\rm{d}}t + {r_t}{V_t}{\rm{d}}t - {r_t}{S_t}\frac{{\partial V}}{{\partial {S_t}}}{\rm{d}}t + \sigma {S_t}\frac{{\partial V}}{{\partial {S_t}}}{\rm{d}}{W_t}\\ = \frac{{\partial V}}{{\partial t}}{\rm{d}}t + \frac{{\partial V}}{{\partial {S_t}}}[({\mu _t} - {q_t}){S_t}{\rm{d}}t + \sigma {S_t}{\rm{d}}{W_t}]\\ \quad + \frac{{\partial V}}{{\partial {J_t}}}{\rm{d}}{J_t} + \frac{1}{2} \cdot \frac{{{\partial ^2}V}}{{\partial S_t^2}}[{\sigma ^2}S_t^2({\rm{d}}t + 2H{t^{2H - 1}}{\rm{d}}t + \lambda {\rm{d}}t)], \end{array}$ |
即
| $\begin{align*} r_t V_t =\dfrac{\partial V}{\partial t}+(r_t -q_t )S_t \dfrac{\partial V}{\partial S_t }+\dfrac{\ln S_t -\ln J_t }{t}J_t \dfrac{\partial V}{\partial J_t }+\dfrac{1}{2}\widehat {\sigma }^2S_t ^2\dfrac{\partial ^2V}{\partial S_t ^2}. \end{align*}$ |
定理4 假设标的资产价格
| $\begin{align} V_c (t,J_t ,S_t )=&(J_t^t S_t^{T-t} )^{\frac{1}{T}}\exp \Big\{r^\ast (T-t)-\int_t^T {r_\theta {\rm d}\theta } +\dfrac{(\sigma _H^\ast )^2}{2}(T^{2H}-t^{2H}) \\[2mm] &+\dfrac{(\sigma _\lambda ^\ast )^2}{2}(T-t)\Big\}N(d_1 )-K{\rm e}^{-\int_t^T {r_\theta {\rm d}\theta } }N(d_2 ),\end{align}$ | (5) |
其中
| $\begin{align*} r^\ast =\dfrac{\int_t^T {(r_\theta -q_\theta )\dfrac{T-\theta }{T}{\rm d}\theta } }{T-t}-\dfrac{(\lambda \sigma ^2+\sigma ^2)(T-t)}{4T}-\dfrac{\sigma ^2(T^{2H}-t^{2H})}{2(T-t)}+\\ \dfrac{H\sigma ^2(T^{2H+1}-t^{2H+1})}{(2H+1)(T-t)},\\[2mm] \sigma _H^\ast =\Big[{1-\dfrac{4H(T^{2H+1}-t^{2H+1})}{(2H+1)(T^{2H}-t^{2H})}+\dfrac{H(T^{2H+2}-t^{2H+2})}{T^2(H+1)(T^{2H}-t^{2H})}} \Big]^{\frac{1}{2}}\sigma ,\\ \sigma _\lambda ^\ast =\dfrac{T-t}{\sqrt 3 T}(\sqrt {\lambda +{1}} \sigma ),\\[2mm] d_1 =\dfrac{(\sigma _\lambda ^\ast )^2(T-t)+(\sigma _H^\ast )^2(T^{2H}-t^{2H})+\dfrac{1}{T}\ln \dfrac{J_t^t S_t^{T-t} }{K^T}+r^\ast (T-t)}{\sqrt {(\sigma _\lambda ^\ast )^2(T-t)+(\sigma _H^\ast )^2(T^{2H}-t^{2H})} },\\[2mm] d_{2} =d_1 -\sqrt {(\sigma _\lambda ^\ast )^2(T-t)+(\sigma _H^\ast )^2(T^{2H}-t^{2H})} ,\\ N(x)=\dfrac{1}{\sqrt {2\pi } }\int_{-\infty }^x {{\rm e}^{-\frac{t^2}{2}}{\rm d}t} . \end{align*}$ |
证明 由定理3知, 几何平均亚式看涨期权在
| $\begin{align*} \xi _t =\dfrac{1}{T}\Big[{t\ln J_t +(T-t)\ln S_t } \Big],V_c (t,J_t ,S_t )=U(t,\xi _t ),\end{align*}$ |
则
| $\begin{align*} &\dfrac{\partial V}{\partial t}=\dfrac{\partial U}{\partial t}+\dfrac{\partial U}{\partial \xi _t }\cdot\dfrac{\ln J_t -\ln S_t }{T},\\[2mm] &\dfrac{\partial V}{\partial S_t }=\dfrac{\partial U}{\partial \xi _t }\cdot\dfrac{T-t}{TS_t },\dfrac{\partial V}{\partial J_t }=\dfrac{\partial U}{\partial \xi _t }\cdot\dfrac{t}{TJ_t },\\[2mm] &\dfrac{\partial ^2V}{\partial S_t ^2}=\dfrac{\partial }{\partial S_t }\Big( {\dfrac{\partial U}{\partial \xi _t }\cdot\dfrac{T-t}{TS_t }} \Big)=\Big( {\dfrac{T-t}{TS_t }} \Big)^2\cdot\dfrac{\partial ^2U}{\partial \xi _t ^2}-\dfrac{T-t}{TS_t ^2}\cdot\dfrac{\partial U}{\partial \xi _t },\end{align*}$ |
那么模型(4) 转化为
| $\begin{align} \left\{\!\! {\begin{array}{l} \dfrac{\partial U}{\partial t}+\Big( {r_t -q_t -\dfrac{{1}}{2}\widehat {\sigma }^{2}} \Big)\dfrac{T-t}{T}\cdot\dfrac{\partial U}{\partial \xi _t }+\dfrac{{1}}{2}\widehat {\sigma }^{2}\Big( {\dfrac{T-t}{T}} \Big)^2\cdot\dfrac{\partial ^2U}{\partial \xi _t ^2}=r_t U_t,\\[4mm] U(T,\xi _T )=({\rm e}^{\xi _T }-K)^+. \end{array}} \right. \end{align}$ | (6) |
令
| $\begin{align*} \tau =\gamma (t),\eta _\tau =\xi _t +\alpha (t),W(\tau ,\eta _\tau )=U(t,\xi _t ){\rm e}^{\beta (t)},\end{align*}$ |
其中
| $\begin{align*} \dfrac{\partial U}{\partial t}&={\rm e}^{-\beta (t)}\Big[{\dfrac{\partial W}{\partial \tau }{\gamma }'(t)-{\beta }'(t)W+\dfrac{\partial W}{\partial \eta _\tau }{\alpha }'(t)} \Big],\\[2mm] \dfrac{\partial U}{\partial \xi _t }&={\rm e}^{-\beta (t)}\dfrac{\partial W}{\partial \eta _\tau },\dfrac{\partial ^2U}{\partial \xi _t ^2}=\dfrac{\partial }{\partial \xi _t }\Big( {{\rm e}^{-\beta (t)}\dfrac{\partial W}{\partial \eta _\tau }} \Big)={\rm e}^{-\beta (t)}\dfrac{\partial ^2W}{\partial \eta _\tau ^2},\end{align*}$ |
代入(6) 式, 整理后得
| $\begin{align} {\gamma }'(t)&\dfrac{\partial W}{\partial \tau }+\Big[{{\alpha }'(t)+(r_t -q_t -\dfrac{{1}}{2}\widehat {\sigma }^{2})\dfrac{T-t}{T}} \Big]\dfrac{\partial W}{\partial \eta _\tau } \\[2mm] & +\dfrac{{1}}{2}\widehat {\sigma }^{2}\Big( {\dfrac{T-t}{T}} \Big)^2\dfrac{\partial ^2W}{\partial \eta _\tau ^2}-(r_t +{\beta }'(t))W=0. \end{align}$ | (7) |
再令
| $\begin{align*} {\gamma }'(t)+\dfrac{{1}}{2}\widehat {\sigma }^{2}\Big( {\dfrac{T-t}{T}} \Big)^2=0,{\alpha }'(t)+\\ \Big( {r_t -q_t -\dfrac{{1}}{2}\widehat {\sigma }^{2}} \Big)\dfrac{T-t}{T}=0,r_t +{\beta }'(t)=0,\end{align*}$ |
结合终止条件
| $\begin{align*} \beta (t)=\int_t^T {r_\theta {\rm d}\theta } ,\\[2mm] \alpha (t)=\int_t^T {(r_\theta -q_\theta ){\rm d}\theta } -\dfrac{\sigma ^2+\lambda \sigma ^2}{4T}(T-t)^2+\\ \dfrac{H\sigma ^2(T^{2H+1}-t^{2H+1})}{T(2H+1)}-\dfrac{\sigma ^2(T^{2H}-t^{2H})}{2},\\[2mm] \gamma (t)=\dfrac{\sigma ^2+\lambda \sigma ^2}{6}\cdot\dfrac{(T-t)^3}{T^2}+\\ \dfrac{H\sigma ^2}{2}\Big[{\dfrac{T^{2H}-t^{2H}}{H}+\dfrac{(T^{2H+2}-t^{2H+2})}{T^2(H+1)}-\dfrac{4(T^{2H+1}-t^{2H+1})}{T(2H+1)}} \Big],\end{align*}$ |
则(7) 式可化为
| $\begin{align} \left\{ {\begin{array}{l} \dfrac{\partial W}{\partial \tau }=\dfrac{\partial ^2W}{\partial \eta _\tau ^2},\\[3mm] W(0,\eta _0 )=({\rm e}^{\eta _0 }-K)^+,\\ \end{array}} \right. \end{align}$ | (8) |
由热传导方程经典解理论可知, (8) 式的解为
| $\begin{align*} W(\tau ,\eta _{_\tau} )&=\dfrac{1}{2\sqrt {{\pi }\tau } }\int_{\ln K}^{+\infty } {({\rm e}^y-K){\rm e}^{-\frac{(y-\eta _{_\tau} )^2}{4\tau }}{\rm d}y} \\[2mm] &=\dfrac{1}{2\sqrt {{\pi }\tau } }\int_{\ln K}^{+\infty } {{\rm e}^y{\rm e}^{-\frac{(y-\eta _{_\tau} )^{2}}{4\tau }}{\rm d}y} -\dfrac{K}{2\sqrt {{\pi }\tau } }\int_{\ln K}^{+\infty } {{\rm e}^{-\frac{(y-\eta _{_\tau} )^{2}}{4\tau }}{\rm d}y} \\[2mm] &=I_1 +I_2 . \end{align*}$ |
令
| $\begin{align*} \dfrac{y-\eta _{_\tau} -2\tau }{\sqrt {2\tau } }=t,\end{align*}$ |
则
| $\begin{align*} I_1 &=\dfrac{1}{2\sqrt {{\pi }\tau } }\int_{\ln K}^{+\infty } {{\rm e}^y{\rm e}^{-\frac{(y-\eta _{_\tau} )^{2}}{4\tau }}{\rm d}y} ={\rm e}^{\tau +\eta _{_\tau}}\dfrac{1}{\sqrt {2{\pi }} }\int_{\ln K}^{+\infty } {{\rm e}^{-\frac{(y-\eta _{_\tau} -2\tau )^2}{4\tau }}{\rm d}y} \\[2mm] &={\rm e}^{\tau +\eta _{_\tau} }\dfrac{1}{\sqrt {2{\pi }} }\int_{-\frac{\eta _{_\tau} +2\tau -\ln K}{\sqrt {2\tau } }}^{+\infty } {{\rm e}^{-\frac{t^2}{2}}{\rm d}t} ={\rm e}^{\tau +\eta _{_\tau } }N\Big( {\dfrac{\eta_{_\tau } +2\tau -\ln K}{\sqrt {2\tau } }} \Big). \end{align*}$ |
再令
| $\begin{align*} \dfrac{y-\eta _{_\tau} }{\sqrt {2\tau } }=t,\end{align*}$ |
则
| $\begin{align*} I_2 =-\dfrac{K}{2\sqrt {{\pi }\tau } }\int_{\ln K}^{+\infty } {{\rm e}^{-\frac{(y-\eta _{_\tau} )}{4\tau }}{\rm d}y} =\\ -\dfrac{K}{\sqrt {2{\pi }} }\int_{-\frac{\eta _{_\tau} -\ln K}{\sqrt {2\pi } }}^{+\infty } {{\rm e}^{-\frac{t^2}{2}}{\rm d}t} =-KN\Big( {\dfrac{\eta _{_\tau}-\ln K}{\sqrt {2{\pi }} }} \Big). \end{align*}$ |
故(8) 式的解为
| $\begin{align} W(\tau ,\eta _{_\tau} )&={\rm e}^{\tau +\eta _{_\tau} }N\Big( {\dfrac{\eta _{_\tau} +2\tau -\ln K}{\sqrt {2\tau } }} \Big)-KN\Big( {\dfrac{\eta _{_\tau} -\ln K}{\sqrt {2\tau } }} \Big) \\ &={\rm e}^{\tau +\eta _{_\tau} }N(d_1 )-KN(d_2 ). \end{align}$ | (9) |
变量还原后有
| $\begin{align*} d_1 =\dfrac{{2}\tau +\eta _\tau -\ln K}{\sqrt {{2}\tau } }=\\ \dfrac{(\sigma _\lambda ^\ast )^2(T-t)+(\sigma _H^\ast )^2(T^{2H}-t^{2H})+\dfrac{1}{T}\ln \dfrac{J_t^t S_t^{T-t} }{K^T}+r^\ast (T-t)}{\sqrt {(\sigma _\lambda ^\ast )^2(T-t)+(\sigma _H^\ast )^2(T^{2H}-t^{2H})} },\\ d_2 =\dfrac{\eta _\tau -\ln K}{\sqrt {{2}\tau } }=\dfrac{\dfrac{1}{T}\ln \dfrac{J_t^t S_t^{T-t} }{K^T}+r^\ast (T-t)}{\sqrt {(\sigma _\lambda ^\ast )^2(T-t)+(\sigma _H^\ast )^2(T^{2H}-t^{2H})} } \\[2mm] =d_1 -\sqrt {(\sigma _\lambda ^\ast )^2(T-t)+(\sigma _H^\ast )^2(T^{2H}-t^{2H})} . \end{align*}$ |
推论1 假设标的资产价格
| $\begin{align} V_p (t,J_t ,S_t )=&-(J_t^t S_t^{T-t} )^{\frac{1}{T}}\exp \Big\{r^\ast (T-t)-\int_t^T {r_\theta {\rm d}\theta } +\dfrac{(\sigma _H^\ast )^2}{2}(T^{2H}-t^{2H}) \\ &+\dfrac{(\sigma _\lambda ^\ast )^2}{2}(T-t)\Big\}N(-d_1 )+K{\rm e}^{-\int_t^T {r_\theta {\rm d}\theta } }N(-d_2). \end{align}$ | (10) |
其他符号与定理4一致.
证明 由边值条件
根据定理4中的定价公式进行数值实验, 讨论定价公式中的各个参数对期权价值的影响.考虑一只标的资产为股票的亚式期权, 其标的股票价格服从混合分数跳-扩散过程(1).假设股票的当前价格
| $\begin{align*} S=80,t=0,T=1,r=0.05,q=0.01,\sigma =0.4,K=80. \end{align*}$ |
对定理给出的亚式期权在
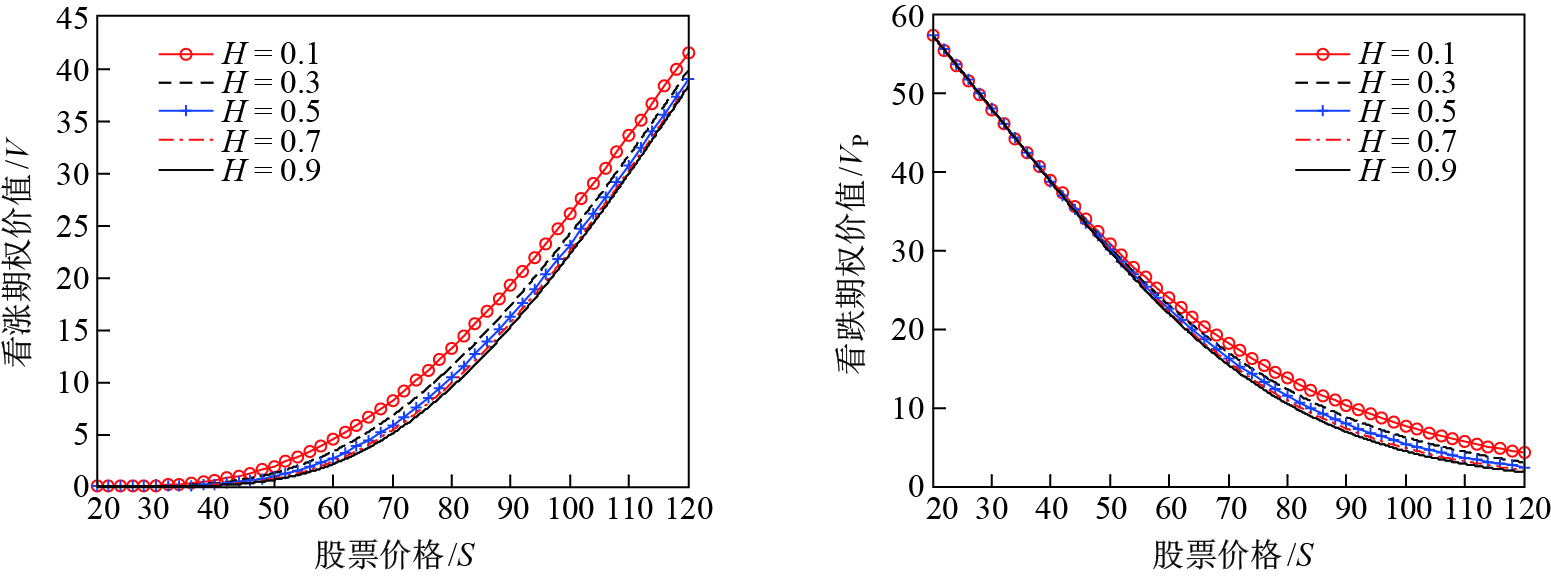
|
图 1 对应不同 |
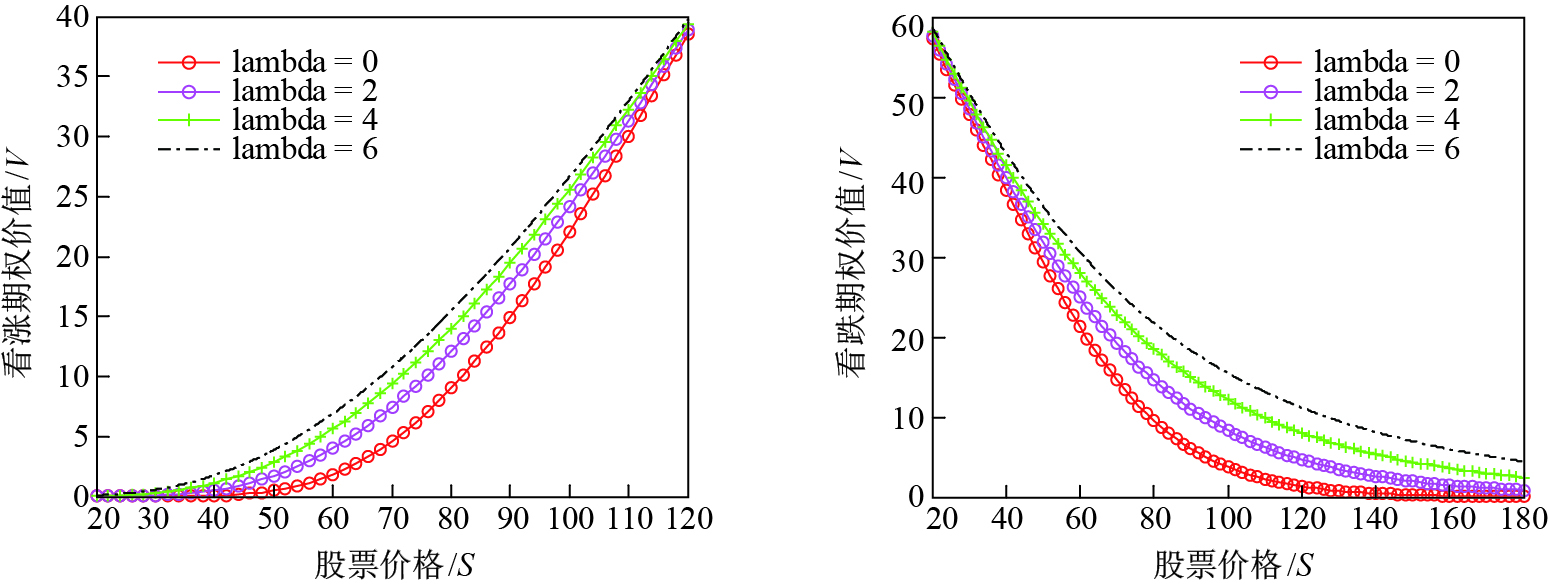
|
图 2 对应不同 |
在参数假设取值不变的情况下, 图 3给出了到期期限和赫斯特指数同时变化时亚式看涨、看跌期权价值的走势情况, 图 4给出了到期期限和跳跃强度同时变化时亚式看涨、看跌期权价值的走势情况.由图 3、图 4可知, 随着期权期限的增加, 期权的价值也在不断增加, 与实际情况相符.
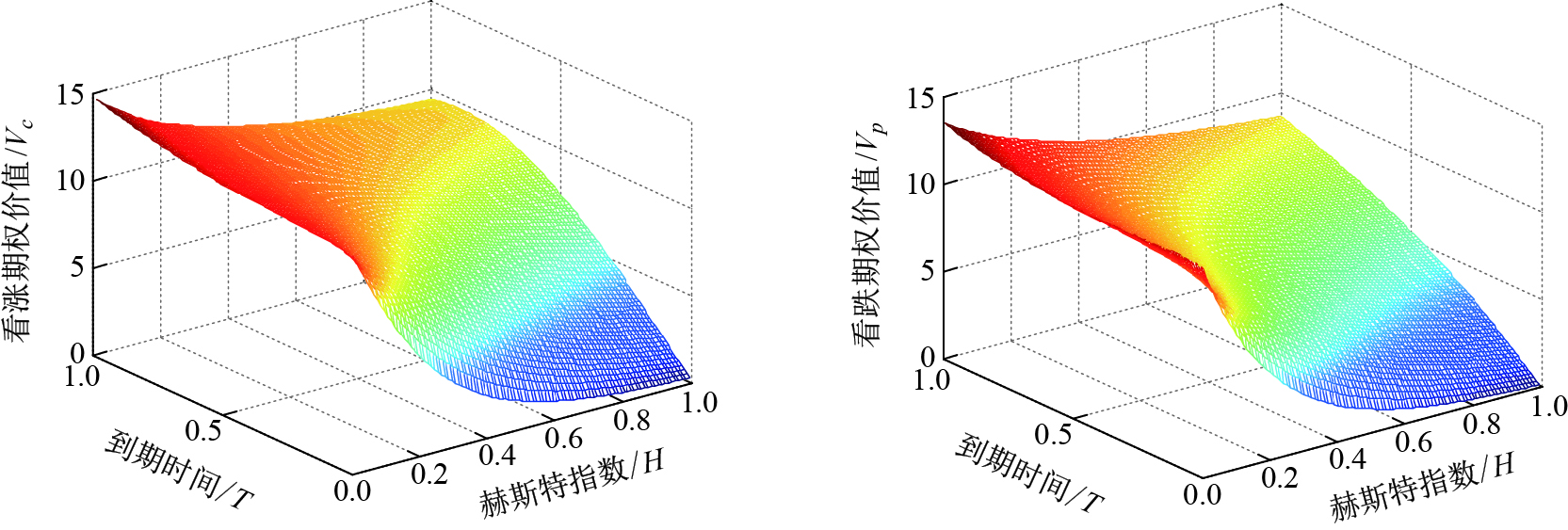
|
图 3 赫斯特指数、到期时间和亚式期权价值的关系 Fig.3 The relation of Hurst exponent, expiry date and Asian option |
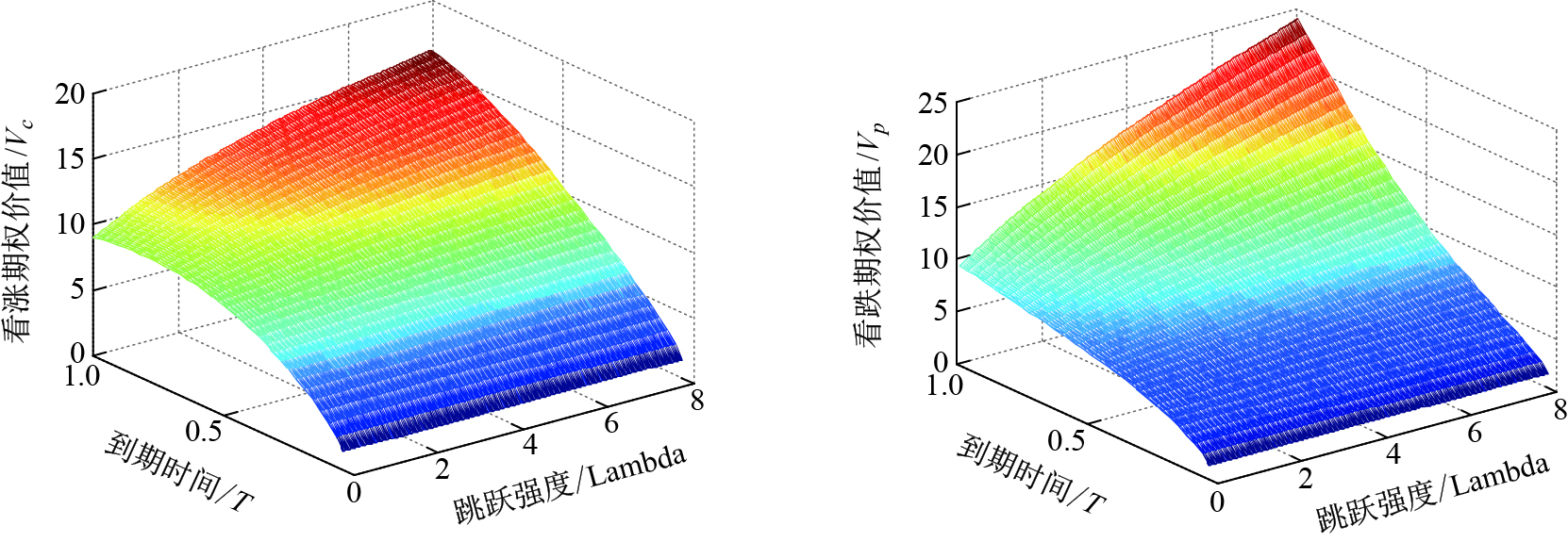
|
图 4 跳跃强度、到期时间和亚式看涨期权价值的关系 Fig.4 The relation of jump intensity, expiry date and Asian option |
本文假设股票价格满足混合分数跳-扩散过程, 通过Itô引理和自融资交易策略推导出混合分数布朗运动下带跳的亚式期权的定价模型, 再运用变量替换法对定价模型进行求解, 得到几何平均亚式期权的解析解.通过数值实验可以看出赫斯特指数与跳跃强度对亚式期权价值有明显的影响.
| [1] | KEMNA A G Z, VORST A C F. A pricing method for options based on average asset values[J]. Journal of Banking and Finance, 1990, 14(1): 113-129. DOI:10.1016/0378-4266(90)90039-5 |
| [2] | WONG H Y, CHEUNG H L. Geometric Asian options: Valuation and calibration with stochastic volatility[J]. Quantitative Finance, 2004, 4(3): 301-314. DOI:10.1088/1469-7688/4/3/006 |
| [3] | CHOU C S, LIN H J. Asian options with jumps[J]. Statistics & Probability, 2006, 6(14): 1983-1993. |
| [4] | CHERIDITO P. Regularizing fractional Brownian motion with a view towards stock price modelling [D]. Zürich: Swiss Federal Institute of Technology, 2001. |
| [5] | CHERIDITO P. Arbirage in fractional Brownian motion models[J]. Finance and Stochastics, 2003, 7(4): 533-553. DOI:10.1007/s007800300101 |
| [6] | KUZNETSOV Y A. The absence of arbitrage in a model with fractal Brownian motion[J]. Russian Mathematical Surveys, 1999, 54(4): 847-848. DOI:10.1070/RM1999v054n04ABEH000191 |
| [7] | ZÄHLE M. Long range dependence, no arbitrage and the Black–Scholes formula[J]. Stochastics and Dynamics, 2002, 2(2): 265-280. DOI:10.1142/S0219493702000406 |
| [8] | MISHURA Y S. Stochastic Calculus for Fractional Brownian Motion and Related Processes[M]. Berlin: Springer, 2008. |
| [9] | WANG X T. Scaling and long-range dependence in option pricing Ⅰ: Pricing European option with transaction costs under the fractional Black–Scholes model[J]. Physica A, 2010, 389(3): 438-444. DOI:10.1016/j.physa.2009.09.041 |
| [10] | WANG X T. Scaling and long-range dependence in option pricing Ⅴ: Multiscaling hedging and implied volatility smiles under the fractional Black–Scholes model with transaction costs[J]. Physica A, 2011, 390(9): 1623-1634. DOI:10.1016/j.physa.2010.12.021 |
| [11] | MEHRDOUST F, SABER N. Pricing arithmetic Asian option under a two-factor stochastic volatility model with jumps[J]. Journal of Statistical Computation and Simulation, 2015, 85(18): 3811-3819. DOI:10.1080/00949655.2015.1046072 |
| [12] | RAMBEERICH N. A high order finite element scheme for pricing options under regime switching jump diffusion processes[J]. Journal of Computational and Applied Mathematics, 2016, 300(2): 83-96. |
| [13] | XIAO W L. Pricing currency options in a fractional Brownian motion with jumps[J]. Economic Modelling, 2010, 27(5): 935-942. DOI:10.1016/j.econmod.2010.05.010 |
| [14] | PENG B. Pricing Asian power options under jump-fraction process[J]. Journal of Economics, Finance and Administrative Science, 2012, 17(33): 2-9. DOI:10.1016/S2077-1886(12)70002-1 |
| [15] | 丰月姣. 带跳混合分数布朗运动下利差期权定价[J]. 佳木斯大学学报, (自然科学版), 2013, 30(6): 922-925. |
| [16] | 孙玉东. 带跳混合分数布朗运动下利差期权定价[J]. 系统科学与数学, 2013, 32(11): 1377-1385. |
| [17] | SHOKROLLAHI F. Actuarial approach in a mixed fractional Brownian motion with jumps environment for pricing currency option[J]. Advances in Difference Equations, 2015, 257(1): 1-8. |




