近年来关于抛物型随机偏微分方程模型的研究越来越受到学者们的关注, 抛物型随机偏微分方程理论已经被广泛应用于随机过程与随机分析、金融数学与金融工程、运筹学与控制论等领域.混合分数布朗运动(mfBm)模型是一类特殊的抛物型随机微分方程, 是高斯过程的衍生过程.众所周知的期权定价理论是金融数学和金融工程的核心理论, 混合分数布朗运动是布朗运动和分数布朗运动的线性组合, 已经被广泛地应用于期权定价理论.文献[1]最早把布朗运动和分数布朗运动组合在一起研究了欧式期权的定价;文献[2]研究了混合分数布朗运动样本轨道的Holder连续性和自相似性; 文献[3-6]已经多次应用跳-扩散模型来刻画股票价格的随机跳行为, 并给出了相应的期权定价公式, 但这种跳-扩散模型无法处理Wick积分, 同时无法定义适合的随机积分来刻画股价的变化, 于是使用混合分数布朗运动来刻画金融资产的波动过程是比较合理的[7-10].由于分数布朗运动的Itô公式和分数Wick-Itô-Skorohod积分所建立的Black-Scholes (简称B-S模型)已经远远超越了B-S模型的定义和属性, 学者们发现所建立的分数B-S模型不能准确地描述资产的浮动收益和金融市场的波动情形[9].事实上, 由于分数布朗运动的自相似性、厚尾性和长程关联性, 使得分数布朗运动既不是Markov过程又不是半鞅, 这给随机分析和随机计算带来了极大的困难.于是有些学者[11-12]提出用混合跳-扩散分数布朗运动(mj-dfBm)模型来刻画金融市场的波动行为.
本文研究一类特殊的混合跳-扩散分数布朗运动模型, 不同于文献[12]的混合跳-扩散分数布朗运动模型, 本文的模型是基于标准布朗运动、分数布朗运动、Poisson过程的线性组合, 利用Itô公式和分数Wick-Itô-Skorohod积分建立了一个新的市场定价模型, 给出了连续支付红利的欧式固定履约和浮动履约回望期权的定价公式, 为了刻画利率的异常波动情形.最后给出的数值模拟与仿真验证了模型的有效性.结果表明, 本文的混合跳-扩散分数布朗运动模型便于计算, 可操作性强, 不但能有效地刻画金融市场的隐含波动率的变化, 而且能够合理地解释金融市场的“微笑现象”.
1 预备及引理定义1[1] 设
| $ M_t^H = \alpha {B_t} + \beta B_t^H, $ |
其中
性质1[2] 混合分数布朗运动
(ⅰ)对任意的
(ⅱ)
(ⅲ)对任意的
| $ {\rm{Cov}}(M_t^H, M_s^H) = {\alpha ^2}(t \wedge s) + \frac{{{\beta ^2}}}{2}({t^{2H}} + {s^{2H}}-|t-s{|^{2H}}), $ |
其中
(ⅳ)对任意的
| $ M_{ht}^H\left( {\alpha, \beta } \right) \buildrel \Delta \over = M_t^H\left( {\alpha {h^{\frac{1}{2}}}, \beta {h^H}} \right), $ |
其中
(ⅴ)当
(ⅵ)
(ⅶ)对任意的
| $ \rm{E}\left[{{{\left( {M_t^H\left( {\alpha, \beta } \right)} \right)}^n}} \right] = \left\{ \begin{array}{l} 0, \;\;\;\;n = 2l + 1, \\ \frac{{\left( {2l} \right)!}}{{{2^l}l!}}{\left( {{\alpha ^2}t + {\beta ^2}{t^{2H}}} \right)^l}, \;\;n = 2l. \end{array} \right. $ |
性质的证明详见文献[2].
引理1[9] 对任意的
| $ {{\tilde E}_t}\left[{{{\rm{e}}^{\sigma \left( {{B_T} + B_T^H} \right)}}} \right] = {{\rm{e}}^{\sigma \left( {{B_T} + B_T^H} \right) + \frac{1}{2}{\sigma ^2}\left( {T -t} \right) + \frac{1}{2}{\sigma ^2}\left( {{T^{2H}} -{t^{2H}}} \right)}}, $ |
其中
引理2[9] 设二元函数
| $ {{\tilde E}_t}\left[{f\left( {\sigma {B_T} + \sigma B_T^H} \right)} \right] = \int_{\bf{R}} {\frac{1}{{\sqrt {2\pi \left[{{\sigma ^2}\left( {T-t + {T^{2H}}-{t^{2H}}} \right)} \right]} }}\exp \left[{-\frac{{{{\left( {x-\sigma {B_t}-\sigma B_t^H} \right)}^2}}}{{2{\sigma ^2}\left( {T - t + {T^{2H}} - {t^{2H}}} \right)}}} \right] \cdot f\left( x \right){\rm{d}}x} . $ |
引理3[9] 设
| $ {{\tilde E}_t}\left[{{1_A}\left( {\sigma {B_T} + \sigma B_T^H} \right)} \right] = \int_{\bf{R}} {\frac{{\exp }}{{\sqrt {2\pi \left[{{\sigma ^2}\left( {T-t + {T^{2H}}-{t^{2H}}} \right)} \right]} }}\left[{-\frac{{{{\left( {x-\sigma {B_t}-\sigma B_t^H} \right)}^2}}}{{2{\sigma ^2}\left( {T - t + {T^{2H}} - {t^{2H}}} \right)}}} \right] \cdot {1_A}\left( x \right){\rm{d}}x} . $ |
设
| $ Z_t^ * = {\sigma _1}B_t^ * + {\sigma _2}{\left( {B_t^H} \right)^ * } = {\sigma _1}{B_t} + \sigma _1^2t + {\sigma _2}B_t^H + \sigma _2^2B_t^{2H}, \;\;\;\;\;\;0 \le t \le T, $ |
其中
| $ E_t^ * \left[{{{\rm{e}}^{{\sigma _1}{B_T} + {\sigma _2}{{\left( {B_T^H} \right)}^ * }}}} \right] = {{\rm{e}}^{{\sigma _1}\left( {{B_T} + B_T^H} \right) + \frac{1}{2}\sigma _1^2\left( {T -t} \right) + \frac{1}{2}\sigma _2^2\left( {{T^{2H}} -{t^{2H}}} \right)}}. $ |
引理4[9] 设
| $ {{\tilde E}_t}\left[{f\left( {{\sigma _1}{B_T} + {\sigma _2}B_T^H} \right)} \right] = \frac{1}{{{X_t}}}{{\tilde E}_t}\left[{f\left( {{\sigma _1}{B_T} + {\sigma _2}B_T^H} \right){X_T}} \right]. $ |
引理5[9] 定义代数流
| $ {X_t} = \exp \left( {-{\sigma _1}{B_t}-\frac{1}{2}\sigma _1^2t-{\sigma _2}B_t^H - \frac{1}{2}\sigma _2^2{t^{2H}}} \right), $ |
则
| $ {F_t} = {{\rm{e}}^{- r\left( {T- t} \right)}}{{\tilde E}_t}\left[F \right], $ |
其中
假设某一支期权的价值
| $ {\rm{d}}{S_t} = \mu {\rm{d}}t + {\sigma _1}{\rm{d}}B_t^H + {\sigma _2}{\rm{d}}{B_t}, $ | (1) |
其中
引理6[11] 设
| $ {\rm{d}}{S_t} = \mu {S_t}{\rm{d}}t + {\sigma _1}{S_t}{\rm{d}}B_t^H + {\sigma _2}{S_t}{\rm{d}}{B_t}, $ |
则
| $ {\rm{d}}{V_t} = \left( {\frac{{\partial V}}{{\partial t}} + \mu {S_t}\frac{{\partial V}}{{\partial S}} + H\sigma _1^2{S_t}{t^{2H-1}}\frac{{{\partial ^2}V}}{{\partial {S^2}}} + \frac{1}{2}\sigma _2^2{S_t}\frac{{{\partial ^2}V}}{{\partial {S^2}}}} \right){\rm{d}}t + {\sigma _1}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}B_t^H + {\sigma _2}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}{B_t}. $ | (2) |
在完备概率空间
引理7 设
| $ {\rm{d}}{S_t} = \mu {S_t}{\rm{d}}t + {\sigma _1}{S_t}{\rm{d}}B_t^H + {\sigma _2}{S_t}{\rm{d}}{B_t} + {\sigma _3}{S_t}{\rm{d}}{P_t}, $ | (3) |
则
| $ \begin{array}{l} {\rm{d}}{V_t} = \left[{\frac{{\partial V}}{{\partial t}} + \mu {S_t}\frac{{\partial V}}{{\partial S}} + \left( {H\sigma _1^2{t^{2H-1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right)S_t^2\frac{{{\partial ^2}V}}{{\partial {S^2}}}} \right]{\rm{d}}t + {\sigma _1}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}B_t^H + {\sigma _2}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}{B_t}\\ \;\;\;\;\;\;\;\; + {\sigma _3}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}{P_t} + \lambda {\rm{E}}\left[{V\left( {S\left( {1 + {j_t}} \right), t} \right)-V\left( {S, t} \right)} \right]{\rm{d}}t, \end{array} $ | (4) |
其中
证 明 假设
| $ {\rm{d}}{P_t} = \left\{ \begin{array}{l} {\rm{P}}\left\{ {{j_t} = {\omega _1}} \right\} = p, \;\;\;\;不发生跳, \\ {\rm{P}}\left\{ {{j_t} = {\omega _2}} \right\} = 1-p, \;\;\;发生跳. \end{array} \right. $ |
在时间区间
设
(ⅰ)如果跳事件不发生, 对于二元可微函数
| $ \begin{array}{l} {\rm{d}}\prod\limits_t {\left( {{\omega _1}} \right)} = {\rm{d}}{V_t}- {\nabla _t}{\rm{d}}{S_t}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = {\left[{\frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H-1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right)S_t^2\frac{{{\partial ^2}V}}{{\partial {S^2}}}} \right]_{\left( {{S_t}, t} \right)}} + {\left( {\frac{{\partial V}}{{\partial S}} -\nabla } \right)_{\left( {{S_t}, t} \right)}}{\rm{d}}{S_t}. \end{array} $ |
(ⅱ)如果跳事件发生, 则
| $ {\rm{d}}\prod\limits_t {\left( {{\omega _2}} \right)} = V\left( {{S_{t + }}} \right)- V\left( {{S_t}, t} \right)- {\nabla _t}\left( {{S_{t + }}- {S_t}} \right) = V\left[{{S_t}\left( {1 + {j_t}} \right), t} \right] -V\left( {{S_t}, t} \right) -{\nabla _t}{j_t}{S_t}. $ |
于是
| $ \begin{array}{l} E\left( {{\rm{d}}\prod\limits_t {} } \right) = r\prod\limits_t {{\rm{d}}t} = \left( {1- \lambda {\rm{d}}t} \right)\left[{{\rm{d}}\prod\limits_t {\left( {{\omega _1}} \right)} } \right] + \lambda {\rm{d}}t\left[{{\rm{d}}\prod\limits_t {\left( {{\omega _2}} \right)} } \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left( {1 - \lambda {\rm{d}}t} \right)\left\{ {{{\left[{\frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H-1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right)S_t^2\frac{{{\partial ^2}V}}{{\partial {S^2}}}} \right]}_{\left( {{S_t}, t} \right)}} + {{\left( {\frac{{\partial V}}{{\partial S}} - \nabla } \right)}_{\left( {{S_t}, t} \right)}}{\rm{d}}{S_t}} \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \lambda {\rm{d}}t\left\{ {V\left[{{S_t}\left( {1 + {j_t}} \right), t} \right] -V\left( {{S_t}, t} \right) -{\nabla _t}{j_t}{S_t}} \right\}. \end{array} $ |
设
| $ \begin{array}{l} \frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H- 1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right){S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}}{\rm{d}}t + \left( {r- \lambda {\sigma _3}} \right)S\frac{{\partial V}}{{\partial S}}\\ \;\;\;\;\;\; + \lambda {\rm{E}}\left[{V\left( {S\left( {1 + {j_t}} \right), t} \right)-V\left( {S, t} \right)} \right] -\left( {r + \lambda } \right)V = 0. \end{array} $ |
于是在混合跳-扩散分数布朗运动模型中, 欧式期权定价模型可以表示为含有期望算子的抛物型积分方程.
仿照引理6的证明, 对二元可微函数
| $ {\rm{d}}{V_t} = \frac{{\partial V}}{{\partial t}}{\rm{d}}t + \frac{{\partial V}}{{\partial S}}{\rm{d}}{S_t} + \frac{1}{2} \cdot \frac{{{\partial ^2}V}}{{\partial {S^2}}}{\left( {{\rm{d}}{S_t}} \right)^2} + o\left( {{\rm{d}}t{\rm{d}}{S_t}} \right). $ | (5) |
由于Cov
| $ \begin{array}{l} {\left( {{\rm{d}}{S_t}} \right)^2} = {\left( {\mu {S_t}{\rm{d}}t + {\sigma _1}{S_t}{\rm{d}}B_t^H + {\sigma _2}{S_t}{\rm{d}}{B_t} + {\sigma _3}{S_t}{\rm{d}}{P_t}} \right)^2}\\ \;\;\;\;\;\;\;\;\;\; = {\mu ^2}S_t^2{\left( {{\rm{d}}t} \right)^2} + \sigma _1^2S_t^2{\left( {{\rm{d}}B_t^H} \right)^2} + \sigma _2^2S_t^2{\left( {{\rm{d}}{B_t}} \right)^2} + \sigma _3^2S_t^2{\left( {{\rm{d}}{P_t}} \right)^2} + 2\left[{\mu {S_t}{\sigma _1}{S_t}{\rm{d}}B_t^H{\rm{d}}t} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\; + \mu {S_t}{\sigma _2}{S_t}{\rm{d}}{B_t}{\rm{d}}t + \mu {S_t}{\sigma _3}{S_t}{\rm{d}}{P_t}{\rm{d}}t + {\sigma _1}{S_t}{\sigma _2}{S_t}{\rm{d}}B_t^H{\rm{d}}{B_t} + {\sigma _1}{S_t}{\sigma _3}{S_t}{\rm{d}}B_t^H{\rm{d}}{P_t}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. { + {\sigma _2}{S_t}{\sigma _3}{S_t}{\rm{d}}B_t^{\rm{d}}{P_t}} \right]\\ \;\;\;\;\;\;\;\;\;\; = 2H\sigma _1^2S_t^2{t^{2H -1}}{\rm{d}}t + \sigma _2^2S_t^2{\rm{d}}t + \lambda \sigma _3^2S_t^2{\rm{d}}t + o\left( {{\rm{d}}t{\rm{d}}{S_t}{\rm{d}}{P_t}} \right). \end{array} $ | (6) |
把式(6) 代入式(5), 可得
| $ \begin{array}{l} {\rm{d}}{V_t} = \frac{{\partial V}}{{\partial t}}{\rm{d}}t + \frac{{\partial V}}{{\partial S}}\left[{\mu {S_t}{\rm{d}}t + {\sigma _1}{S_t}{\rm{d}}B_t^H + {\sigma _2}{S_t}{\rm{d}}{B_t} + {\sigma _3}{S_t}{\rm{d}}{P_t}} \right]\\ \;\;\;\;\;\;\;\;\; + \frac{1}{2}\frac{{{\partial ^2}V}}{{\partial {S^2}}}\left[{2H\sigma _1^2S_t^2{t^{2H-1}}{\rm{d}}t + \sigma _2^2S_t^2{\rm{d}}t + \lambda \sigma _3^2S_t^2{\rm{d}}t} \right]\\ \;\;\;\;\;\; = \left[{\frac{{\partial V}}{{\partial t}} + \mu {S_t}\frac{{\partial V}}{{\partial S}} + \left( {H\sigma _1^2{t^{2H-1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right)S_t^2\frac{{{\partial ^2}V}}{{\partial {S^2}}}} \right]{\rm{d}}t + {\sigma _1}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}B_t^H\\ \;\;\;\;\;\;\;\;\; + {\sigma _2}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}{B_t} + {\sigma _3}{S_t}\frac{{\partial V}}{{\partial S}}{\rm{d}}{P_t} + \lambda {\rm{E}}\left[{V\left( {S\left( {1 + {j_t}} \right), t} \right)-V\left( {S, t} \right)} \right]{\rm{d}}t. \end{array} $ |
证毕.
2.2 分数Wick-Itô-Skorohod积分与混合跳-扩散分数随机微分方程定义2[13] 定义函数
| $ \int_{\bf{R}} {{Y_t}{\rm{d}}B_t^H} : = \int_{\bf{R}} {{Y_t}\diamondsuit B_t^H{\rm{d}}t}, $ |
其中
引理8[13](分数Girsanov公式Ⅰ) 假设
| $ \int_{\delta '\left( {\bf{R}} \right)} {\psi \left( {\omega + \tilde \gamma } \right){\rm{d}}{P^H}\left( \omega \right)} = \int_{\delta '\left( {\bf{R}} \right)} {\psi \left( \omega \right) \cdot {\rm{exp}}\diamondsuit \left( {\left\langle {\omega, \gamma } \right\rangle } \right){\rm{d}}{P^H}\left( \omega \right)}, $ |
其中
| $ \left\langle {\omega, \gamma } \right\rangle : = \int_{\bf{R}} {\int_{\bf{R}} {\omega \left( s \right)\gamma \left( t \right)\varphi \left( {s, t} \right){\rm{d}}s{\rm{d}}t} }, \;\;\;\;\omega, \gamma \in \delta \left( {\bf{R}} \right). $ |
引理8*[13](分数Girsanov公式Ⅱ) 设
| $ {\left\langle {K, f} \right\rangle _H} = {\left\langle {\gamma, f} \right\rangle _{{L^2}\left( {\bf{R}} \right)}}, {\rm{supp}}\;f \subset \delta \left( {\bf{R}} \right). $ |
令
引理9[13](不同白噪声空间上的Wick乘积) 设
| $ F{\diamondsuit _P}G = F{\diamondsuit _Q}G, $ |
其中
假设无风险利率的债券价格
| $ \left\{ \begin{array}{l} {\rm{d}}{S_t} = {r_t}{S_t}{\rm{d}}t, \\ {S_0} = 1. \end{array} \right. $ | (7) |
根据定义2, 引理8和引理9, 可以考虑如下混合跳-扩散分数随机微分方程
| $ \left\{ \begin{array}{l} {\rm{d}}{S_t} = {S_t}\diamondsuit \left[{\left( {r-q-\lambda {\sigma _3}} \right){\rm{d}}t + {\sigma _1}{\rm{d}}B_t^H + {\sigma _2}{\rm{d}}{B_t} + {\sigma _3}{\rm{d}}{P_t}} \right], \\ {S_t} = S, \end{array} \right. $ |
其中
设
| $ \begin{array}{l} {\rm{d}}\prod { = {\rm{d}}V- \nabla \diamondsuit {\rm{d}}S- \nabla q\diamondsuit S{\rm{d}}t} \\ \;\;\;\;\;\;\; = \frac{{\partial V}}{{\partial t}}{\rm{d}}t + \frac{{\partial V}}{{\partial J}} + \frac{1}{2}\lambda {\sigma _3}{S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}}{\rm{d}}t + \frac{{\partial V}}{{\partial S}}{\rm{d}}S + H\sigma _1^2{S^2}{t^{2H- 1}}\frac{{{\partial ^2}V}}{{\partial {S^2}}}{\rm{d}}t + \frac{1}{2}{\sigma _2}{S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}}{\rm{d}}t\\ \;\;\;\;\;\;\;\;\; + {\sigma _3}\frac{{\partial V}}{{\partial S}}{\rm{d}}{P_t} - \nabla \diamondsuit {\rm{d}}S - \nabla q\diamondsuit S{\rm{d}}t\\ \;\;\;\;\;\;\; = \left[{\frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H-1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right){S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}}-\nabla q\diamondsuit S} \right]{\rm{d}}t + \frac{{\partial V}}{{\partial J}}{\rm{d}}J\\ \;\;\;\;\;\;\;\;\; + {\sigma _3}\frac{{\partial V}}{{\partial S}}{\rm{d}}{P_t} + \left( {\frac{{\partial V}}{{\partial S}} -\nabla } \right)\diamondsuit {\rm{d}}S. \end{array} $ | (8) |
由于
| $ \begin{array}{l} d\prod = \left[{\frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H-1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right){S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}}-\nabla q\diamondsuit S} \right]{\rm{d}}t + \frac{{\partial V}}{{\partial J}}{\rm{d}}J\\ \;\;\;\;\;\;\;\;\; + {\sigma _3}\frac{{\partial V}}{{\partial S}}{\rm{d}}{P_t} + \left( {\frac{{\partial V}}{{\partial S}} - \nabla } \right)\diamondsuit {\rm{d}}S\\ \;\;\;\;\;\;\; = \left[{\frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H-1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right){S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}} + \frac{{\partial V}}{{\partial {J_n}}} \cdot \frac{{{\rm{d}}{J_n}}}{{{\rm{d}}t}}-\nabla q\diamondsuit S} \right]{\rm{d}}t\\ \;\;\;\;\;\;\;\;\; + {\sigma _3}\frac{{\partial V}}{{\partial S}}{\rm{d}}{P_t} + \left( {\frac{{\partial V}}{{\partial S}} -\nabla } \right)\diamondsuit {\rm{d}}S. \end{array} $ |
令
| $ \begin{array}{l} \frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H- 1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right){S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}} + \frac{{{{\left( {\frac{S}{{{J_n}}}} \right)}^{n- 1}}S- {J_n}}}{{nt}} \cdot \frac{{\partial V}}{{\partial {J_n}}} + \left( {r + q - \lambda {\sigma _3}} \right)S\frac{{\partial V}}{{\partial S}}\\ \;\;\;\;\;\;\;\; + \lambda {\rm{E}}\left[{V\left( {S\left( {1 + {j_t}} \right), t} \right)-V\left( {S, t} \right)} \right] -\left( {r + \lambda } \right)V = 0, \end{array} $ | (9) |
其中
固定
| $ \begin{array}{l} \frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H- 1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right){S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}} + \left( {r- q- \lambda {\sigma _3}} \right)S\frac{{\partial V}}{{\partial S}}\\ \;\;\;\;\;\;\;\; + \lambda {\rm{E}}\left[{V\left( {S\left( {1 + {j_t}} \right), t} \right)-V\left( {S, t} \right)} \right] -\left( {r + \lambda } \right)V = 0, \end{array} $ | (10) |
| $ V\left( {t, S, J} \right) = J-S, $ | (11) |
| $ \frac{{\partial V}}{{\partial J}}\left| {_{S = J}} \right. = 0. $ | (12) |
回望期权是指该期权持有者在期权到期日可以观察期权有效期内标的资产价格的变化过程, 通过选择资产价格的最高价格或最低价格进行交易, 是一种典型复杂的新型奇异期权.设
| $ M_{{T_0}}^T = \mathop {\max }\limits_{{T_0} \le \xi \le T} {S_\xi } $ |
和
| $ m_{{T_0}}^T = \mathop {\min }\limits_{{T_0} \le \xi \le T} {S_\xi }. $ |
回望期权有固定履约回望期权和浮动履约回望期权两类.浮动履约回望看涨期权是指该期权持有者在回望期内有权利以最低的交易价格买入资产, 浮动履约回望看跌期权是指该期权持有者在回望期内有权利以最高的交易价格买出资产, 因此
引理10[14] 假设一支欧式固定履约回望看涨期权的到期实际支付额为
| $ \begin{array}{l} {c_{{\rm{fixed}}}}\left( {K, M, t} \right) = \\ \left\{ \begin{array}{l} \exp \left\{ {- r\left( {T- t} \right)} \right\}{E_Q}\left[{\max \left( {M_t^T-K, 0} \right)} \right], M \le K\\ \exp \left\{ { - r\left( {T - t} \right)} \right\}\left( {M - K} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}{E_Q}\left[{\max \left( {M_t^T-K, 0} \right)} \right], M > K \end{array} \right.\\ = \exp \left\{ { - r\left( {T - t} \right)} \right\}\max \left( {M - K, 0} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}{E_Q}\left[{\max \left( {M_t^T-K, 0} \right)} \right], \end{array} $ |
同理, 欧式固定履约回望看跌期权的到期实际支付额为
| $ {p_{{\rm{fixed}}}}\left( {K, m, t} \right) = \exp \left\{ {- r\left( {T- t} \right)} \right\}\max \left( {M- m, 0} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}{E_Q}\left[{\max \left( {M-m, 0} \right)} \right]. $ |
引理11[14] 假设一支欧式浮动履约回望看涨期权的到期实际支付额为
| $ \begin{array}{l} {c_{{\rm{floating}}}}\left( {{S_T}, m, t} \right) = \exp \left\{ {- r\left( {T- t} \right)} \right\}{E_Q}\left[{{S_T}-\min \left( {m, m_t^T} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \exp \left\{ { - r\left( {T - t} \right)} \right\}{E_Q}\left[{\left( {{S_T}-m} \right) + \max \left( {m-m_t^T, 0} \right)} \right], \end{array} $ |
当欧式浮动履约回望看跌期权的到期实际支付额为
| $ \begin{array}{l} {p_{{\rm{floating}}}}\left( {{S_T}, M, t} \right) = \exp \left\{ {- r\left( {T- t} \right)} \right\}{E_Q}\left[{\max \left( {M, M_t^T} \right)-{S_T}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \exp \left\{ { - r\left( {T - t} \right)} \right\}{E_Q}\left[{\max \left( {M_t^T-M, 0} \right)-\left( {{S_T}-M} \right)} \right]. \end{array} $ |
设
| $ \begin{array}{l} 0 = \frac{{\partial V}}{{\partial t}} + \left( {H\sigma _1^2{t^{2H- 1}} + \frac{1}{2}\sigma _2^2 + \frac{1}{2}\lambda \sigma _3^2} \right){S^2}\frac{{{\partial ^2}V}}{{\partial {S^2}}} + \left( {r- q- \lambda {\sigma _3}} \right)S\frac{{\partial V}}{{\partial S}} - \left( {r + \lambda } \right)V\\ \;\;\;\;\; + \left\{ \begin{array}{l} \lambda {\rm{E}}\left[{V\left( {S\left( {1 + {j_t}} \right), \min \left\{ {J, S\left( {1 + {j_t}} \right)} \right\}, t} \right)} \right], 回望看涨, \\ \lambda {\rm{E}}\left[{V\left( {S\left( {1 + {j_t}} \right), \max \left\{ {J, S\left( {1 + {j_t}} \right)} \right\}, t} \right)} \right], 回望看跌, \end{array} \right. \end{array} $ | (13) |
| $ V\left( {t, S, J} \right) = J-S, $ | (14) |
其中
| $ \sum { = \left\{ \begin{array}{l} \left\{ {\left( {S, J} \right):0 < J \le S < \infty } \right\}, 回望看涨, \\ \left\{ {\left( {S, J} \right):0 < S \le J < \infty } \right\}, 回望看跌. \end{array} \right.} $ | (15) |
终端条件为
| $ \frac{{\partial V}}{{\partial J}}\left| {_{S = J}} \right. = 0. $ | (16) |
类似于引理10和引理11的推导, 在(13)-(16) 的条件下, 下面以定理的形式给出欧式固定履约回望期权和浮动履约回望期权的定价公式.
定理1 设到期日为
| $ \begin{array}{l} {P_{{\rm{fixed}}}}\left( {K, m, t} \right) = \exp \left\{ {- r\left( {T- t} \right)} \right\}\left( {K- m} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}KN\left( { - {d_2}} \right) - \exp \left\{ {\left( { - q - \lambda {\sigma _3}} \right)} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { \times \left( {T - t} \right)} \right\}mN\left( { - {d_1}} \right) + \frac{r}{{2\left( { - q - {\lambda _3}} \right)}}\left[{\exp \left\{ {\left( {-q-\lambda {\sigma _3}} \right)\left( {T-t} \right)} \right\}mN\left( {{d_1}} \right)} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - \exp \left\{ { - r\left( {T - t} \right)} \right\}\exp \left\{ {\frac{{2K\left( { - q - \lambda {\sigma _3}} \right)}}{r}} \right\}N\left( {d_1^r} \right)} \right], \end{array} $ | (17) |
| $ \begin{array}{l} {C_{{\rm{fixed}}}}\left( {K, m, t} \right) = \exp \left\{ {- r\left( {T- t} \right)} \right\}\left( {K- m} \right) + \exp \left\{ {\left( { - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\}MN\left( {{d_1}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \exp \left\{ { - r\left( {T - t} \right)} \right\}KN\left( { - {d_2}} \right) + \frac{r}{{2\left( { - q - \lambda {\sigma _3}} \right)}}\left[{\exp \left\{ {-r\left( {T-t} \right)} \right\}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { \times \exp \left\{ {\frac{{2K\left( {-q - \lambda {\sigma _3}} \right)}}{r}} \right\}N\left( {d_1^r} \right) - \exp \left\{ {\left( { - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\}N\left( {{d_1}} \right)} \right\}, \end{array} $ | (18) |
其中
| $ \begin{array}{l} {d_1} = \\ \frac{{\ln \frac{{S\sum\limits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{K} + \left( {r -q -\lambda {\sigma _3}} \right)\left( {T - t} \right) + \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \frac{1}{2}\left( {\sigma _2^2 + \lambda \sigma _3^2} \right)\left( {T - t} \right)}}{{\sqrt {2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}, \end{array} $ |
| $ \begin{array}{l} {d_2} = \\ \frac{{\ln \frac{{S\sum\limits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{K} -\left( {r -q - \lambda {\sigma _3}} \right)\left( {T - t} \right) + \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \frac{1}{2}\left( {\sigma _2^2 + \lambda \sigma _3^2} \right)\left( {T - t} \right)}}{{\sqrt {2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}, \end{array} $ |
| $ d_1^r = {d_1}-\frac{{2\left( {-q-\lambda {\sigma _3}} \right)\left( {T - t} \right)}}{{\sqrt r }}, $ |
证 明 在风险中性金融市场, 根据引理5和引理10, 到期日为
| $ \begin{array}{l} {P_{{\rm{fixed}}}}\left( {K, m, t} \right) = \exp \left\{ {- r\left( {T- t} \right)} \right\}\max \left( {K- m, 0} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}{E_Q}\left[{\max \left( {K-m_t^T, 0} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \exp \left\{ { - r\left( {T - t} \right)} \right\}\max \left( {K - m, 0} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \times {{\tilde E}_{{P_H}}}\left[{\min \left( {K-m_t^T, 0} \right){1_{K > m_t^T}}\left| {F_t^H} \right.} \right], \end{array} $ | (19) |
其中
设
| $ \left( {r-q-\lambda {\sigma _3}} \right)t = {\sigma _1}\left( {\hat B_T^H-\hat B_t^H} \right) + {\sigma _2}\left( {{{\hat B}_T} - {{\hat B}_t}} \right) + {\sigma _3}\left( {{{\hat P}_T} - {{\hat P}_t}} \right), $ |
则
| $ m_t^T = {S_t} \cdot \exp \left\{ {\left[{r-q-\lambda {\sigma _3}\left( {T-t} \right)} \right] \times \left[{-\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right)-\frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right]} \right\}, $ |
注意到Poisson跳过程的跳跃强度为
| $ \begin{array}{l} {S_T} = {S_t}\prod\limits_{i = 1}^{{N_{T- t}}} {\exp \left\{ {\left[{r-q-\lambda {\sigma _3}\left( {T-t} \right)} \right] \cdot \left[{-\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right)-\frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right]} \right\}} \\ \;\;\;\; = \sum\limits_{n = 0}^\infty {{\rm{P}}\left( {{N_t} = n} \right)} \cdot \left\{ {{S_t}\prod\limits_{i = 1}^n {\exp \left[{\left( {{\sigma _1}\left( {\hat B_T^H-\hat B_t^H} \right) + {\sigma _2}\left( {{{\hat B}_T}-{{\hat B}_t}} \right) + {\sigma _3}\left( {{{\hat P}_T}-{{\hat P}_t}} \right)} \right)} \right.} } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. { \times \left( { - \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) - \frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right)} \right]} \right\}\\ \;\;\;\; = \sum\limits_{n = 0}^\infty {\frac{{{{\rm{e}}^{ - \lambda \left( {T - t} \right)}}{\lambda ^n}{{\left( {T - t} \right)}^n}}}{{n!}}} \left\{ {{S_t}\prod\limits_{i = 1}^n {\exp \left[{\left( {{\sigma _1}\left( {\hat B_T^H-\hat B_t^H} \right) + {\sigma _2}\left( {{{\hat B}_T}-{{\hat B}_t}} \right) + {\sigma _3}\left( {{{\hat P}_T}-{{\hat P}_t}} \right)} \right)} \right.} } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. { \times \left( { - \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) - \frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right)} \right]} \right\}\\ \;\;\;\; = {S_t}\sum\limits_{n = 0}^\infty {\frac{{{{\rm{e}}^{ - \lambda \left( {T - t} \right)}}{\lambda ^n}{{\left( {T - t} \right)}^n}}}{{n!}}{\varepsilon _n}} \times \exp \left[{\left( {{\sigma _1}\left( {\hat B_T^H-\hat B_t^H} \right) + {\sigma _2}\left( {{{\hat B}_T}-{{\hat B}_t}} \right) + {\sigma _3}\left( {{{\hat P}_T}-{{\hat P}_t}} \right)} \right)} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. { \times \left( { - \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) - \frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right)} \right], \end{array} $ |
于是
| $ \begin{array}{l} m_t^T = {S_t}\sum\limits_{n = 0}^\infty {\frac{{{{\rm{e}}^{- \lambda \left( {T- t} \right)}}{\lambda ^n}{{\left( {T- t} \right)}^n}}}{{n!}}{\varepsilon _n}} \times \exp \left[{\left( {{\sigma _1}\left( {\hat B_T^H-\hat B_t^H} \right) + {\sigma _2}\left( {{{\hat B}_T}-{{\hat B}_t}} \right) + {\sigma _3}\left( {{{\hat P}_T}-{{\hat P}_t}} \right)} \right)} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. { \times \left( { - \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) - \frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right)} \right], \end{array} $ |
对其两端取对数可得
| $ \begin{array}{l} \ln m_t^T = \ln \left( {{S_t}\sum\limits_{n = 0}^\infty {\frac{{{{\rm{e}}^{- \lambda \left( {T- t} \right)}}{\lambda ^n}{{\left( {T- t} \right)}^n}}}{{n!}}{\varepsilon _n}} } \right) + \left[{{\sigma _1}\left( {\hat B_T^H-\hat B_t^H} \right) + {\sigma _2}\left( {{{\hat B}_T}-{{\hat B}_t}} \right) + {\sigma _3}\left( {{{\hat P}_T}-{{\hat P}_t}} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\; + \left[{-\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right)-\frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right]. \end{array} $ |
利用分数Girsanov定理可知
| $ \begin{array}{l} d_1^ * = \ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ - 1}}{\varepsilon _n}} }}{K} + \left( {r - q + \lambda {\sigma _3}} \right)\left( {T - t} \right)\\ \;\;\;\;\;\;\; + \left[{-\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right)-\frac{1}{2}\sigma _2^2\left( {T - t} \right) - \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right]. \end{array} $ |
且
| $ \begin{array}{l} {d_1} = \frac{{{\sigma _1}\hat B_t^H + {\sigma _2}{{\hat B}_t} + {\sigma _3}{{\hat P}_t}- d_1^ * }}{{\sqrt {2\sigma _1^2\left( {{T^{2H}}- {t^{2H}}} \right) + \sigma _2^2\left( {T- t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}\\ \;\;\;\; = \left\{ {\ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T - t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ - 1}}{\varepsilon _n}} }}{K} + \left( {r - q + \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right.\\ \;\;\;\;\left. { + \left[{\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right) + \frac{1}{2}\sigma _2^2\left( {T-t} \right) + \frac{1}{2}\lambda \sigma _3^2\left( {T-t} \right)} \right]} \right\}\\ \;\;\;\; \times {\left\{ {\sqrt {2\sigma _1^2\left( {{T^{2H}} -{t^{2H}}} \right) + \sigma _2^2\left( {T -t} \right) + \lambda \sigma _3^2\left( {T -t} \right)} } \right\}^{ - 1}}, \end{array} $ |
根据引理5, 可得
| $ \begin{array}{l} {{\tilde E}_{{{\hat P}_H}}}\left[{{1_{K > m_t^T}}\left| {F_t^H} \right.} \right] = {{\tilde E}_{{{\hat P}_H}}}\left[{{1_{d_1^ * < {\sigma _1}\hat B_t^H + {\sigma _2}{{\hat B}_T} + {\sigma _3}{{\hat P}_T} < + \infty }}\left| {F_t^H} \right.} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \int_{d_1^ * }^{ + \infty } {\frac{1}{{\sqrt {2\pi \left[{2\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right) + \sigma _2^2\left( {T-t} \right) + \lambda \sigma _3^2\left( {T-t} \right)} \right]} }}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \times \exp \left[{-\frac{{{{\left( {x-{\sigma _1}\hat B_t^H-{\sigma _2}{{\hat B}_t} - {\sigma _3}\hat P} \right)}^2}}}{{2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)}}} \right]{\rm{d}}x\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \int_{ -\infty }^{{d_1}} {\frac{1}{{\sqrt {2\pi } }}\exp \left( { -\frac{{{z^2}}}{2}} \right){\rm{d}}z} = N\left( {{d_1}} \right). \end{array} $ | (20) |
考察
| $ {\sigma _1}{\left( {B_t^H} \right)^ * } + {\sigma _2}B_t^ * + {\sigma _3}P_t^ * = {\sigma _1}\left( {\hat B_t^H-{\sigma _1}t} \right) + {\sigma _2}\left( {{{\hat B}_t}-{\sigma _2}t} \right) + {\sigma _3}\left( {{{\hat P}_t}-{\sigma _3}t} \right), $ |
再次利用分数Girsanov定理可知
| $ {X_t} = \exp \left( {{\sigma _1}\hat B_t^H + {\sigma _2}{{\hat B}_t} + {\sigma _3}{{\hat P}_t}-\sigma _1^2{t^{2H}}-\frac{1}{2}\sigma _2^2t-\frac{1}{2}\lambda \sigma _3^2t} \right), $ |
则
| $ \begin{array}{l} \;\;\;{{\tilde E}_{{{\hat P}_H}}}\left[{m_t^T{1_{K > m_t^T}}\left| {F_t^H} \right.} \right]\\ = {S_t}\exp \left\{ {\left( {r - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\}{{\tilde E}_{{{\hat P}_H}}}\\ \left[{{X_T}{1_{d_1^ * < {\sigma _1}\hat B_t^H + {\sigma _2}{{\hat B}_T} + {\sigma _3}{{\hat P}_T} < + \infty }}\left( {{\sigma _1}\hat B_T^H + {\sigma _2}{{\hat B}_T} + {\sigma _3}{{\hat P}_T}} \right)\left| {F_t^H} \right.} \right]\\ = {S_t}\exp \left\{ {\left( {r - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\}{{\tilde E}_{P_H^ * }}\\ \left[{{1_{d_2^ * < \left[{{\sigma _1}{{\left( {\hat B_T^H} \right)}^ * } + {\sigma _2}\hat B_T^ * + {\sigma _3}\hat P_T^ * } \right] < + \infty }}\left( {{\sigma _1}{{\left( {\hat B_T^H} \right)}^ * } + {\sigma _2}\hat B_T^ * + {\sigma _3}\hat P_T^ * } \right)\left| {F_t^H} \right.} \right]\\ = {S_t}\exp \left\{ {\left( {r -q -\lambda {\sigma _3}} \right)\left( {T -t} \right)} \right\} \times \int_{ - \infty }^{{d_2}} {\frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{z^2}}}{2}} \right){\rm{d}}z} \\ = {S_t}\exp \left\{ {\left( {r - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\} \times N\left( {{d_2}} \right), \end{array} $ | (21) |
其中
| $ \begin{array}{l} {d_2} = \frac{{{\sigma _1}{{\left( {\hat B_t^H} \right)}^ * } + {\sigma _2}\hat B_t^ * + {\sigma _3}\hat P_t^ *- d_2^ * }}{{\sqrt {2\sigma _1^2\left( {{T^{2H}}- {t^{2H}}} \right) + \sigma _2^2\left( {T- t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}\\ \;\;\;\; = \left\{ {\ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T - t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ - 1}}{\varepsilon _n}} }}{K} - \left( {r - q + \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right.\\ \;\;\;\;\left. { + \left[{\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right) + \frac{1}{2}\sigma _2^2\left( {T-t} \right) + \frac{1}{2}\lambda \sigma _3^2\left( {T-t} \right)} \right]} \right\}\\ \;\;\;\; \times {\left\{ {\sqrt {2\sigma _1^2\left( {{T^{2H}} -{t^{2H}}} \right) + \sigma _2^2\left( {T -t} \right) + \lambda \sigma _3^2\left( {T -t} \right)} } \right\}^{ - 1}}, \end{array} $ |
| $ \begin{array}{l} d_2^ * = \ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ - 1}}{\varepsilon _n}} }}{K} - \left( {r - q + \lambda {\sigma _3}} \right)\left( {T - t} \right)\\ \;\;\;\;\;\;\; + {\sigma _1}{\left( {B_t^H} \right)^ * } + {\sigma _2}B_t^ * + {\sigma _3}P_t^ * + \left[{\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right) + \frac{1}{2}\sigma _2^2\left( {T-t} \right) + \frac{1}{2}\lambda \sigma _3^2\left( {T-t} \right)} \right]. \end{array} $ |
根据式(19)-(21), 以及引理10, 可得
| $ \begin{array}{l} \;\;\;{P_{{\rm{fixed}}}}\left( {K, m, t} \right)\\ = \exp \left\{ {- r\left( {T- t} \right)} \right\}\max \left( {K- m, 0} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}{{\tilde E}_{{P_H}}}\left[{\min \left( {K-m_t^T, 0} \right){1_{K > m_t^T}}\left| {F_t^H} \right.} \right] \end{array} $ |
| $ \begin{array}{l} = \exp \left\{ {- r\left( {T- t} \right)} \right\}{{\tilde E}_{{P_H}}}\left[{\max \left( {K-m, 0} \right){1_{K > m}}\left| {F_t^H} \right.} \right] + \exp \left\{ { -r\left( {T -t} \right)} \right\}\\ \times \int_0^{ + \infty } {{\rm{P}}\left( {\max \left( {K -m_t^T, 0} \right) \ge x} \right){\rm{d}}x}\\ \left( {0 \le \max \left( {K - m, 0} \right) \le K, 0 \le \max \left( {K - m_t^T, 0} \right) \le K} \right) \end{array} $ |
| $ = \exp \left\{ {-r\left( {T-t} \right)} \right\}\left( {K-m} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}\int_0^K {{\rm{P}}\left( {K - m_t^T \ge x} \right){\rm{d}}x} $ |
| $ = \exp \left\{ {-r\left( {T-t} \right)} \right\}\left( {K-m} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}\int_0^K {{\rm{P}}\left( {\ln \frac{{m_t^T}}{m} \le \ln \frac{z}{m}} \right){\rm{d}}z} \left( {z = K - z} \right) $ |
| $ = \exp \left\{ {-r\left( {T-t} \right)} \right\}\left( {K-m} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}\int_0^{\ln \frac{K}{m}} {m\exp \left( y \right){\rm{P}}\left( {\ln \frac{{m_t^T}}{m} \le y} \right){\rm{d}}y\left( {y = \ln \frac{2}{m}} \right)} $ |
| $ \begin{array}{l} = \exp \left\{ {- r\left( {T- t} \right)} \right\}\left( {K- m} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}\int_0^{\ln \frac{K}{m}} {m\exp \left( y \right)} \\ \;\;\; \times P\left\{ {N\left[{\left( {y- \ln \frac{{m\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{K} + \left( {r -q -\lambda {\sigma _3}} \right)\left( {T - t} \right)} \right.} \right.} \right. \end{array} $ |
| $ \begin{array}{l} \;\;\;\left. { + \sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right) + \frac{1}{2}\sigma _2^2\left( {T-t} \right) + \frac{1}{2}\lambda \sigma _3^2\left( {T-t} \right)} \right)\\ \;\;\;\left. { \times {{\left( {\sqrt {2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} } \right)}^{ - 1}}} \right] \end{array} $ |
| $ \begin{array}{l} \;\;\; + \exp \left[{\frac{{ry}}{{2\left( {-q-\lambda {\sigma _3}} \right)}}} \right] \times N\left[{\left( {\ln \frac{{m\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{K}} \right.} \right.\\ \left. {\;\;\; + \left( {r -q -\lambda {\sigma _3}} \right)\left( {T - t} \right) + \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \frac{1}{2}\sigma _2^2\left( {T - t} \right) + \frac{1}{2}\lambda \sigma _3^2\left( {T - t} \right)} \right) \end{array} $ |
| $ \begin{array}{l} \left. {\left. {\;\;\; \times {{\left( {\sqrt {2\sigma _1^2\left( {{T^{2H}}-{t^{2H}}} \right) + \sigma _2^2\left( {T-t} \right) + \lambda \sigma _3^2\left( {T-t} \right)} } \right)}^{ - 1}}} \right]} \right\}{\rm{d}}y\\ = \exp \left\{ { - r\left( {T - t} \right)} \right\}\left( {K - m} \right) + \exp \left\{ { - r\left( {T - t} \right)} \right\}KN\left( { - {d_2}} \right)\\ - \exp \left\{ {\left( { - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\}mN\left( { - {d_1}} \right)\\ + \frac{r}{{2\left( { - q - \lambda {\sigma _3}} \right)}}\\ \left[{\exp \left\{ {\left( {-q-\lambda {\sigma _3}} \right)\left( {T-t} \right)} \right\}mN\left( { - {d_1}} \right) - \exp \left\{ { - r\left( {T - t} \right)} \right\}\exp \left\{ {\frac{{2K\left( { - q - \lambda {\sigma _3}} \right)}}{r}} \right\}N\left( {d_1^r} \right)} \right], \end{array} $ |
其中
| $ \begin{array}{*{20}{l}} {{d_1} = }\\ {\frac{{\ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{K} + \left( {r -q -\lambda {\sigma _3}} \right)\left( {T - t} \right) + \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \frac{1}{2}\left( {\sigma _2^2 + \lambda \sigma _3^2} \right)\left( {T - t} \right)}}{{\sqrt {2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}, } \end{array} $ |
| $ \begin{array}{*{20}{l}} {{d_2} = }\\ {\frac{{\ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{K} -\left( {r -q - \lambda {\sigma _3}} \right)\left( {T - t} \right) + \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \frac{1}{2}\left( {\sigma _2^2 + \lambda \sigma _3^2} \right)\left( {T - t} \right)}}{{\sqrt {2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}, } \end{array} $ |
| $ d_1^r = {d_1}-\frac{{2\left( {-q-\lambda {\sigma _3}} \right)\left( {T - t} \right)}}{{\sqrt r }}. $ |
利用同样的证明过程可以得到式(18).
对照引理11以及定理1, 可以给出欧式浮动履约回望看跌和看涨期权的价格公式.
定理2 设到期日为
| $ \begin{array}{l} {C_{{\rm{floating}}}}\left( {{S_T}, m, t} \right) = \\ \exp \left\{ {- r\left( {T- t} \right)} \right\}{S_T}N\left( {- {d_2}} \right) - \exp \left\{ {\left( { - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\}mN\left( { - {d_1}} \right) + \frac{r}{{2\left( { - q - \lambda {\sigma _3}} \right)}}\\ \times \left[{\exp \left\{ {\left( {-q-\lambda {\sigma _3}} \right)\left( {T-t} \right)} \right\}mN\left( {{d_1}} \right) - \exp \left\{ { - r\left( {T - t} \right)} \right\}\exp \left\{ {\frac{{2{S_T}\left( { - q - \lambda {\sigma _3}} \right)}}{r}} \right\}N\left( {d_1^r} \right)} \right], \end{array} $ | (22) |
| $ \begin{array}{l} {P_{{\rm{floating}}}}\left( {{S_T}, M, t} \right) = \\ \exp \left\{ {\left( {- q- \lambda {\sigma _3}} \right)\left( {T- t} \right)} \right\}MN\left( { - {d_1}} \right) - \exp \left\{ { - r\left( {T - t} \right)} \right\}{S_T}N\left( { - {d_2}} \right) + \frac{r}{{2\left( { - q - \lambda {\sigma _3}} \right)}}\\ \times \left[{\exp \left\{ {-r\left( {T-t} \right)} \right\}\exp \left\{ {\frac{{2{S_T}\left( {-q - \lambda {\sigma _3}} \right)}}{r}} \right\}N\left( {d_1^r} \right) - \exp \left\{ {\left( { - q - \lambda {\sigma _3}} \right)\left( {T - t} \right)} \right\}N\left( {{d_1}} \right)} \right], \end{array} $ | (23) |
| $ \begin{array}{*{20}{l}} {{d_1} = }\\ {\frac{{\ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{{{S_T}}} + \left( {r -q -\lambda {\sigma _3}} \right)\left( {T - t} \right) + \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \frac{1}{2}\left( {\sigma _2^2 + \lambda \sigma _3^2} \right)\left( {T - t} \right)}}{{\sqrt {2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}, } \end{array} $ |
| $ \begin{array}{*{20}{l}} {{d_2} = }\\ {\frac{{\ln \frac{{S\sum\nolimits_{n = 0}^\infty {{\lambda ^n}{{\left( {T- t} \right)}^n}\exp \left[{-\lambda \left( {T-t} \right)} \right]{{\left( {n!} \right)}^{ -1}}{\varepsilon _n}} }}{K} -\left( {r -q - \lambda {\sigma _3}} \right)\left( {T - t} \right) + \sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \frac{1}{2}\left( {\sigma _2^2 + \lambda \sigma _3^2} \right)\left( {T - t} \right)}}{{\sqrt {2\sigma _1^2\left( {{T^{2H}} - {t^{2H}}} \right) + \sigma _2^2\left( {T - t} \right) + \lambda \sigma _3^2\left( {T - t} \right)} }}, } \end{array} $ |
| $ d_1^r = {d_1}-\frac{{2\left( {-q-\lambda {\sigma _3}} \right)\left( {T - t} \right)}}{{\sqrt r }}, $ |
其中
证明过程类似于定理1.
注记1 根据定理1和定理2, 欧式固定履约回望看涨期权和看跌期权之间满足如下的平价关系
| $ {C_{{\rm{fixed}}}}\left( {K, M, t} \right) = {P_{{\rm{floating}}}}\left( {{S_T}, M, t} \right) + \exp \left\{ {-r\left( {T-t} \right)} \right\}\max \left( {M-K, 0} \right). $ |
Eberlein E和Papapantoleon A[16]也得到了风险资产在Lévy跳过程的环境下欧式固定履约回望看涨期权和欧式浮动履约回望看跌期权之间的平价关系公式.
注记2 在本文的混合跳-扩散分数布朗运动模型中, 当
对不含有跳过程的纯混合分数布朗运动(pmfBm)模型, 含有跳过程的混合分数布朗运动(jmfBm)模型[7], 以及本文的混合跳-扩散分数布朗运动(mj-dfBm)模型分别作一般假设下的理论价格对比, 为了更突出模型之间的异同, 参数的选择没有选取已有的实证数据, 所有模拟结果由Matlab运行生成, 模型所用到的所有参数值见表 1.
| 表 1 不同模型下选择的参数值 Tab.1 The valuations of the chosen parameters used in these models |
把表 1的相应参数分别代入到各类模型中, 记
| 表 2 不同模型下欧式固定履约回望看跌期权价格 Tab.2 European lookback fixed strike put option prices for various models |
比较
考虑混合跳-扩散分数布朗运动下欧式固定履约回望看跌期权定价模型各参数的变化, 在取不同的跳参数值时, 相应的
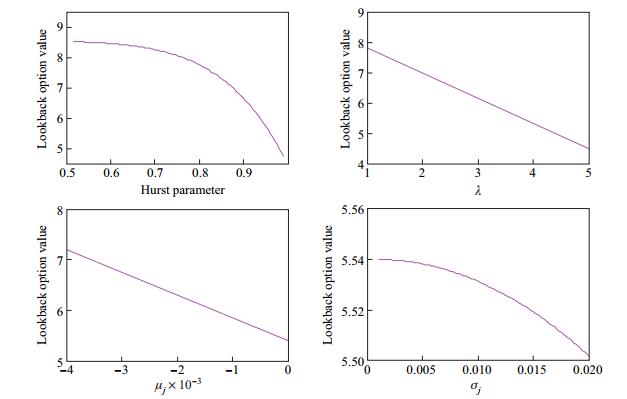
|
图 1 不同参数下欧式固定履约回望看跌期权价格 Fig.1 European lookback fixed strike put option prices for various parameters |
继续考虑混合跳扩散分数布朗运动下欧式固定履约回望看跌期权定价模型的隐含波动率变化, 在选定参数
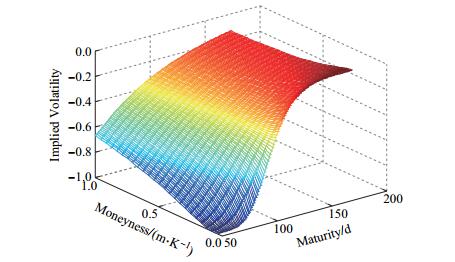
|
图 2 混合跳-扩散分数布朗运动下欧式固定履约回望看跌期权模型的隐含波动率模拟 Fig.2 Smile surface generated by the mj-dfBm model |
本文的定价模型考虑了标准布朗运动、分数布朗运动、Poisson过程的线性组合, 利用Itô公式和分数Wick-Itô-Skorohod积分建立了一个新的市场定价模型, 给出了连续支付红利的欧式固定履约和浮动履约回望期权的定价公式, 通过具体数值和相关参数对定价公式的模拟验证, 表明该模型在刻画期权在短期交割或长期交割前表现出的异常波动跳现象是相当合理的并且是有效性的, 从回望看跌期权价格的递减表现上来看, 明显略快于其他模型, 更加接近不确定金融市场.本文的混合跳-扩散分数布朗运动模型便于计算, 可操作性强, 不但能有效地刻画金融市场的隐含波动率的变化, 而且能够合理地解释金融市场的“微笑”现象.本文的结论在合理解释金融现象的同时, 也丰富了期权定价理论, 对其他类型奇异期权的研究以及一些复杂金融衍生品定价的研究具有参考意义.
| [1] | CHERIDITO P. Mixed fractional Brownian motion[J]. Bernoulli, 2001, 7(6): 913-934. DOI:10.2307/3318626 |
| [2] | MOUNIR Z L. On the mixed fractional Brownian motion[J]. Journal of Applied Mathematics and Stochastic Analysis, 2006: 1-9. |
| [3] | 姜礼尚, 罗俊. 跳扩散模型下永久美式看跌期权定价[J]. 系统工程理论与实践, 2008, 28(2): 10-18. |
| [4] | CHANG M A, CHINHYUNG C, KEENWAN P. The price of foreign currency options under jump-diffusion processes[J]. Journal of Futures Markets, 2007, 27(7): 669-695. DOI:10.1002/(ISSN)1096-9934 |
| [5] | 陈超. 标的资产价格服从跳-扩散过程的脆弱期权定价模型[J]. 工程数学学报, 2008, 25(6): 1129-1132. |
| [6] | 彭斌, 彭菲. 基于跳-分形模型的美式看涨期权定价[J]. 数学的实践与认识, 2014, 44(24): 1-9. |
| [7] | 徐峰, 郑石秋. 混合分数布朗运动驱动的幂期权定价模型[J]. 经济数学, 2010, 27(2): 8-12. |
| [8] | 孙玉东, 师义民. 混合分数布朗运动下亚式期权定价[J]. 经济数学, 2011, 28(1): 49-51. |
| [9] | XIAO W L, ZHANG W G. Pricing model for equity warrants in a mixed fractional Brownian environment and its algorithm[J]. Physica A, 2012, 391(24): 6418-6431. DOI:10.1016/j.physa.2012.07.041 |
| [10] | SUN L. Pricing currency options in the mixed fractional Brownian motion[J]. Physica A, 2013, 392(16): 3441-3458. DOI:10.1016/j.physa.2013.03.055 |
| [11] | 杨朝强. 一类混合跳-扩散分数布朗运动的欧式回望期权定价[J]. 山东大学学报(理学版), 2013, 48(6): 67-74. |
| [12] | FOAD S, ADEM K. Pricing currency option in a mixed fractional Brownian motion with jumps environment[J]. Mathematical Problems in Engineering, 2014, 2014(1): 1-13. |
| [13] | BIAGINI F, HU Y Z. Stochastic Calculus for Fractional Brownian Motion and Applications[M]. London: Springer-Verlag, 2008. |
| [14] | YUE K K. Mathematical Models of Financial Derivatives[M]. 2nd ed. Berlin: Springer, 2008: 201-211. |
| [15] | XIAO W L, ZHANG W G. Pricing currency options in a fractional Brownian motion with jumps[J]. Economic Modelling, 2010, 27(5): 935-942. DOI:10.1016/j.econmod.2010.05.010 |
| [16] | EBERLEIN E, PAPAPANTOLENO A. Equivalence of floating and fixed strike Asian and lookback options[J]. Stochastic Processes and Their Applications, 2005, 115(1): 31-40. DOI:10.1016/j.spa.2004.07.003 |



