2. 西南林业大学 图书馆, 昆明, 650224
2. Library of South West Forestry University, Kunming 650224, China
随着移动互联网和Web2.0的快速发展, 互联网已经渗入到人们生活工作的方方面面, 随之产生了大量的用户行为数据.例如, 用户的位置信息数据、用户对电影或音乐的评分数据、电子商务应用中用户对商品做出评价而产生的用户评分数据, 这些数据的不断产生使得用户行为建模成为可能.用户行为建模对个性化信息服务、行为定向等问题的解决有重要的作用; 分析用户行为数据, 建立用户偏好模型是实现和提供这些服务的基础和关键, 具有重要意义.
一般的用户评分数据包含用户属性信息、评分对象属性信息以及用户评分.用户偏好是用户对事物的喜好或倾向性的选择, 不能被直接观测到.用户评分数据反映了用户偏好, 用户偏好也从一定程度上决定了用户的评分.实际中, 用户对事物的喜好或倾向选择会受到事物本身所固有的多个属性的影响.例如, MovieLens数据集[1]包括用户信息、电影信息和评分, 电影信息包括多个维度的电影属性, 如年代、类型、语言等; 而用户对每个维度的电影属性都会有相应的喜好或倾向, 形成了多个维度的用户偏好.这意味着, 用户对电影最终的倾向会受多维偏好的影响, 对多维偏好的分析是获得精确用户倾向或喜好的必要条件.同时, 多个维度的用户偏好之间也可能相互影响, 这使得准确描述多维偏好、建立用户偏好模型具有实际意义, 也具有一定的挑战.
近年来, 关于多维用户偏好建模已经有了一些研究, 使用向量模型或主题模型等表达多维用户偏好[2-6].例如, LDA(Latent Dirichlet Allocation)[4]是一种具有代表性的主题模型, SVD(Singular Value Decomposition)[6]是协同过滤中常见的评分预测算法, 这些模型能够表达预先给定的依赖关系.但是, 评分数据中各个属性间存在相互影响的依赖关系, 且具有不确定性, 例如, 评分、用户属性以及电影属性之间会相互影响, 且影响的方向以及程度不确定.这些模型能够表达预先给定的依赖关系, 但评分数据中任意的、不确定性的依赖关系的表示, 还需进一步探索.
贝叶斯网(BN, Bayesian Network)[7]是由一组节点构成的有向无环图(DAG, Directed Acyclic Graph), 其中每个节点都有一个条件概率表(CPT, Conditional Probability Table). BN是表达属性间任意的依赖关系以及不确定性的有效工具[8], 且具有优秀的推理能力.使用隐变量描述用户偏好, 将隐变量引入BN构成含隐变量的BN, 简称为隐变量模型(LVM, Latent Variable Model), 是本文研究的基本思想.为了客观有效地描述评分数据中任意的、不确定的依赖关系, 我们以多个隐变量分别描述多个维度的用户偏好, 以隐变量模型作为表示各变量之间依赖关系的基本知识框架, 进而从用户评分数据构建隐变量模型.
隐变量无法被直接观测到[9], 参数的计算需要先对隐变量进行填充, 不能直接使用最大似然估计来计算参数.期望最大算法(EM, Expectation Maximization)[10]是一种可以对隐变量进行填充并寻找参数最大似然或最大后验概率的有效算法.结构期望最大算法(SEM, Structure Expectation Maximization)[11]是一种结合了EM算法的结构打分搜索方法, 能够在EM迭代中直接优化打分, 可以有效的构建隐变量模型的结构.基于此, 本文基于EM算法提出隐变量模型参数的计算方法, 基于SEM算法提出结构的构建方法.
一方面, SEM算法和EM算法的运行结果均会受初始结构和约束条件的影响[12]. Friedman等[11]指出, 随机的初始结构会导致SEM算法很难得到一个有意义的运行结果. Jin等[13]也已经证明, 随机初始参数也会导致EM算法容易收敛到局部极值点.基于此, 为了保证模型构建的有效性, 本文对EM算法和SEM算法进行了扩展, 从初始值的约束限定出发, 提出了基于约束条件的模型构建方法.另一方面, EM算法和SEM算法的执行, 都涉及大量的迭代计算, 而每一次迭代计算又涉及NP困难的概率计算, 计算复杂度较高. Spark是一种基于内存的并行计算框架, 所有中间结果暂存在内存中, 可以处理高复杂度的问题, 而且擅长迭代计算.基于此, 本文使用Spark计算框架实现基于约束的EM算法以及基于约束的SEM算法的并行执行.
总的来说, 本文的主要内容可以概括如下:
从评分数据出发构建偏好模型方面, Zhao等[14]提出评价数据较少情形下的商品服务评估模型.文献[15]基于上下文感知的方法来获取用户偏好.文献[16]以条件偏好网络模型来构建用户偏好.文献[17]基于上下文最小二乘支持向量机来构建用户偏好.在多维偏好建模方面, 也出现了大量研究. Kassak[2]等以对象的多个属性特征来描述对象, 以向量描述多维偏好. Zhao等[5]融合了类型主题模型和地域主题模型, 构建了一种二维偏好模型(对地域的偏好和对类型的偏好).这些方法只能表达预先给定的相互影响的依赖关系, 而数据中任意形式的依赖关系的表示, 还需进一步研究.
基于BN或隐变量模型的单维用户偏好建模方面, Kim等[9]用隐变量表示用户的评价行为, 用含隐变量的BN来构建偏好模型. Gao等[18]用隐变量描述用户对电影类型的偏好, 进而构建偏好模型. Huang等[19]从旅游的领域知识构建BN, 在此基础上估计用户的旅游偏好. Chapelle等[20]使用隐变量刻画用户兴趣, 预定义模型的结构, 提出了用以描述用户点击行为的动态贝叶斯网模型.这些方法为我们的研究提供了参考, 但是以隐变量模型为基本框架来构建多维偏好模型的方法还需进一步研究.
在利用BN进行多维偏好建模方面, Huete等[21]用BN表示用户画像, 将用户对商品多个维度的评分视为隐变量, 根据各维度评分与最终评分之间的特定关系构建BN结构, 进而根据BN的推理来预测商品的评分. Auffenberg等[22]用多个隐变量来刻画用户应对温度变化可能的多个类型的倾向选择, 以给定的依赖关系来构建BN结构.上述基于隐变量模型的偏好建模方法, 以隐变量表示用户偏好, 以含隐变量的BN来构建偏好模型, 这些方法为我们的研究提供了参考, 但通常是先给定BN的图结构.以隐变量模型为基本框架, 从评分数据构建能客观表达不确定性的多维偏好模型, 还需进一步研究.
基于数据分析的隐变量模型构建方面, 我们[23]基于MapReduce模型, 从打分搜索的方法入手, 以MDL的数值来打分选择贝叶斯网模型. Yoshinori等[24]对搜索空间进行了分布式的处理, 基于动态规划的思想提出了一种最优结构的搜索算法.这些隐变量模型构建方法为本文的研究提供了参考, 但针对含多个隐变量的BN构建方法还需进一步探索.
2 相关定义例如, 电影评分数据中,
下面给出多维偏好模型的形式化定义.
定义1 一个多维用户偏好模型是一个含多个隐变量的贝叶斯网, 即多维隐变量模型(MLVM, Multiple Latent Variables Model), 表示为二元组
为了保证模型构建的有效性, 本文对EM算法和SEM的初始值进行约束限定.本文从用户评分数据出发, 根据用户偏好和隐变量的特定含义给出模型构建的初始值需要满足的约束条件.
约束1 第
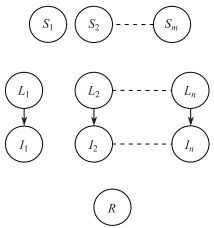
|
图 1 结构约束 Fig.1 Structural constraint |
约束2 用
| $\begin{align} P(R=R_1|L, I, n_1>n_2)>P(R=R_1|L, I, n_2>n_1). \end{align}$ | (1) |
EM算法从一个随机初始参数开始, 先对数据集中隐变量的值进行填充, 然后计算并更新参数, 迭代直至收敛.假设数据集
E-步
首先, 根据当前缺值数据集
| $\begin{align} P(L=j|D_t, \theta_t)=\dfrac{P(L=j, D_t|\theta_t)}{\displaystyle \sum^{c}_{j=1}P(L=j, D_t|\theta_t)}. \end{align}$ | (2) |
其中,
进而, 根据公式(3) 计算充分统计量
| $\begin{align} m^{t}_{ijk}=\sum^{m}_{l=1}P(V_i=k, \pi(V_i)=j|D'_t). \end{align}$ | (3) |
M-步
然后, 使用公式(4) 计算本次迭代所求的参数值
| $\begin{align} \theta_{t+1}=\dfrac{m^{t}_{ijk}}{\sum\limits^{r_i}_{k=1}m^{t}_{ijk}}. \end{align}$ | (4) |
为了确保收敛的效率, 我们给定一个阈值来度量两次迭代所得参数的相似程度.如公式(5) 所示,
| $\begin{align} S(\theta_t, \theta_{t+1})=\ln P(D_{t+1}|\theta_{t+1})-\ln P(D_t|\theta_{t}). \end{align}$ | (5) |
EM算法迭代的每一步, 都会对隐变量的值进行填充、并生成新的CPT.每个隐变量都有多个可能的填充值, 对所有隐变量的值进行填充后, 评分数据集中的数据量随隐变量个数的增加呈阶乘数量级增长.同时, 隐变量CPT的规模也随隐变量父节点个数的增加呈阶乘数量级扩大.数据填充时大量的中间结果及对其频繁的读写操作, 对数据存储及读写速度提出了新挑战, 传统的单任务计算框架已经无法满足需求.
因此, 本文基于Spark框架设计了并行的参数计算方法.首先随机产生一组满足约束2的初始参数; 然后, 以这组参数作为EM算法的初始值, 执行以下步骤.
1) 数据集被分割成
2) 根据公式(4) 计算参数.
步骤1) 和2) 迭代执行, 直至收敛, 执行流程如图 2所示, 上述思想见算法1.
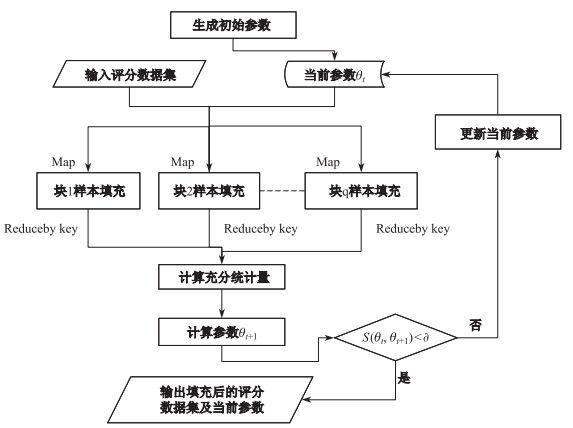
|
图 2 算法1的流程 Fig.2 Process of Algorithm |
| 算法1: CPT-Learn( |
| 输入: |
| |
| |
| |
| |
| 输出: |
| |
| 1: |
| 2: if |
| 3:随机产生一组满足约束2的初始参数 |
| 4: |
| 5: end if |
| 6: for |
| 7: pair |
| key |
| value |
| Emit(key, value) |
| } |
| 8:Rpair |
| for |
| key |
| // |
| Emit(key, value) |
| end for |
| } |
| 9: |
| 10: |
| 11: if |
| 12: return |
| 13: end if |
| 14: end for |
例如, 表 1给出了用户评分数据片段的示例,
| 表 1 数据集片断 Tab.1 Fragment of data set |
| 表 2 填充后数据 Tab.2 Filled data |
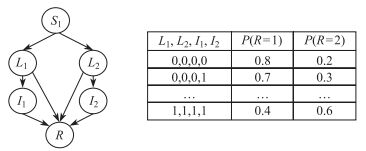
|
图 3 当前结构和部分参数 Fig.3 Current structure and partial parameters |

|
图 4 参数集 Fig.4 Set of parameters |
SEM算法是一种基于打分搜索的结构构建算法, 贝叶斯信息准则(BIC, Bayesian Information Criterion)是一种常用的有效打分标准, 能在缺值样本前提下对结构进行打分.其计算公式如公式(6) 所示.
| $\begin{align} {\rm BIC}(\varphi|D)=\sum\limits^{n}_{i=1}\sum\limits^{q_i}_{j=1} \sum\limits^{r_i}_{k=1}m_{ijk}\ln\dfrac{m_{ijk}}{m_{ij}}-\sum\limits^{n}_{i=1} \dfrac{q_i(r_i-1)}{2}\ln N. \end{align}$ | (6) |
其中,
本文基于Spark框架设计模型结构构建的并行算法.首先从约束1出发, 随机产生一组满足约束1的初始结构, 然后随机生成一组满足约束2的初始参数.以生成的初始参数和结构作为SEM算法的初始值, 对每个节点:
1) 调用算法1对数据集中的隐变量值进行填充, 并将充分统计量持久化(保存直至本次迭代结束), 以便计算BIC分数值.收集完整数据集以及充分统计量, 通过加、减和转边生成一系列候选模型.
2) 为每个候选模型分配一个Map函数, 由步骤1) 得到充分统计量计算候选模型的BIC分数; 收集每个Map函数的结果, 选择BIC分数最大的作为当前模型, 并调用算法1构建参数.
上述步骤1) 和2) 迭代执行, 直到所有节点遍历结束.上述思想见算法2.
| 算法2: DAG-Learn( |
| 输入: |
| |
| |
| |
| |
| V_num:节点个数 |
| 输出: ( |
| 1: if |
| 2:随机产生满足约束1的BN结构 |
| 3: |
| 4: end if |
| 5: |
| 6: |
| 7: oldScore |
| 8: newScore |
| 9: for |
| 10: |
| 11: Rpair |
| |
| key |
| value |
| Emit(key, value) |
| } |
| 12: Rpair.foreach{Line= |
| if value |
| |
| newScore |
| end if |
| } |
| 13: if newScore |
| 14: ( |
| 15: ( |
| 16: oldScore |
| 17: else |
| 18: return |
| 19: end if |
| 20: end for |
例如, 图 5为当前模型及参数, 执行算法2, 对节点
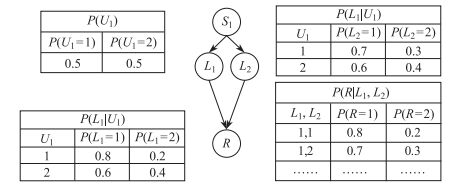
|
图 5 当前结构和参数 Fig.5 Current structure and parameters |
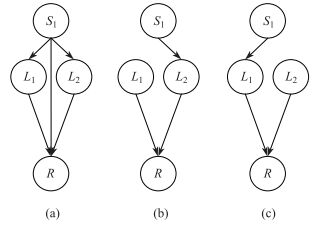
|
图 6 候选结构 Fig.6 Candidate structure |
本文使用MovieLens数据集[1]作为测试数据, 包括3 952条电影信息数据, 1 000 209条评分数据以及6 040条用户信息.预处理后的数据集共有1 000 209行, 每行数据是一次用户评分记录; 每行数据都有2个用户属性, 5个电影属性以及1个评分值.实验环境如下:在两台主频2.3 GHZ的双路HP服务器上开辟了7台虚拟机, 1台作为主节点、其余6台作为计算节点搭建Spark集群; 主节点分配4个CPU核心16 GB内存, 每个计算节点分配8个CPU核心16 GB内存, 将一个CPU计算核心简称为C.
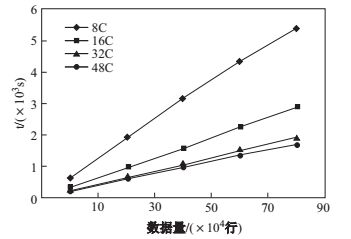
4.1 参数计算效率测试我们首先测试了隐变量模型包括7个节点(其中2个隐变量)情况下, 不同计算核心个数、不同数据量情形下算法1的执行时间, 如图 7所示.可以看出, 算法1的执行时间随着数据量的增大而增加, 并且计算节点越多执行时间越少.这说明算法1能够在较大数据量情形下能有效地学习隐变量模型的参数, 且具有较好的可扩展性.
|
图 7 算法1的执行时间 Fig.7 Execution time of Algorithm 1 |
加速比是串行算法的执行时间与并行算法的执行时间的比值.随着数据量的增加, 算法1在不同计算核心时的加速比如图 8所示.可以看出, 算法1的加速比随计算核心的增多而增大, 随数据量的增大而逐渐稳定, 这说明算法1有较好的可扩展性.
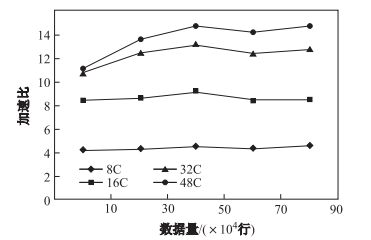
|
图 8 算法1的加速比 Fig.8 Speedup ratio of Algorithm 1 |
然后, 我们测试了10万行数据时, 隐变量个数对算法1执行时间的影响.如图 9所示, 算法1的执行时间随隐变量的个数增加呈阶乘数量级增加, 其原因在于隐变量的增加会使得填充后的数据量呈阶乘数量级增加, 算法1的执行时间也随之上升.
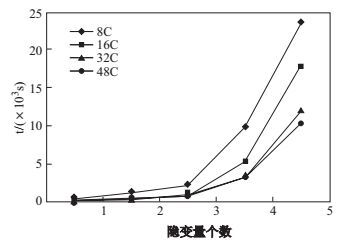
|
图 9 隐变量个数增加时算法1的执行时间 Fig.9 Execution time of Algorithm 1 with the increase of latent variables |
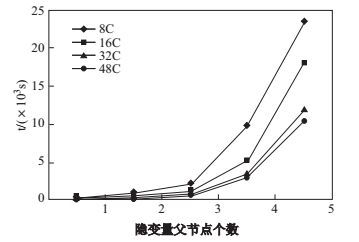
接着, 我们测试了10万行数据、2个隐变量(与加速比实验保持一致)的情况下, 算法1的执行时间与隐变量父节点个数的关系, 如图 10所示.可以看出算法1的执行时间随隐变量父节点的增多而快速增大.这说明, 随着隐变量父节点数的增加, 模型的依赖关系更加密集, 条件概率表的规模成阶乘数量级增大, 算法1的执行时间也随之上升, 隐变量父节点数是影响模型参数计算效率的瓶颈.
|
图 10 隐变量父节点数增加时算法1的执行时间 Fig.10 Execution time of Algorithm 1 with the increase of parent nodes of the latent variable |
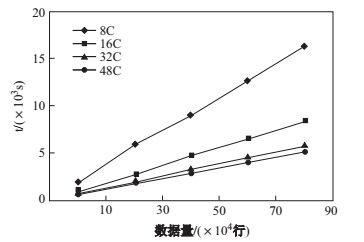
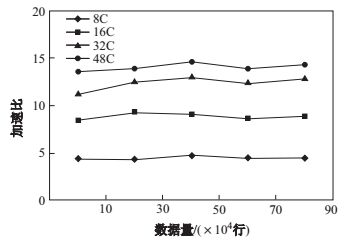
类似地, 本文对算法2进行了测试.首先测试隐变量模型包括7个节点(其中2个隐变量)的情况下, 不同数据量情形下算法2的执行时间, 如图 11所示.可以看出, 算法2的执行时间随着数据量的增加而增加, 计算节点越多、执行时间越少, 这说明算法2在较大数据量情形下能有效地构建隐变量模型结构, 且具有较好可扩展性.我们进一步测试了算法2的加速比, 如图 12所示, 可以看出, 算法2的加速比随计算核心数的增加而增大, 说明算法2具有较好可扩展性.
|
图 11 算法2的执行时间 Fig.11 Execution time of Algorithm 2 |
|
图 12 算法2的加速比 Fig.12 Speedup ratio of Algorithm 2 |
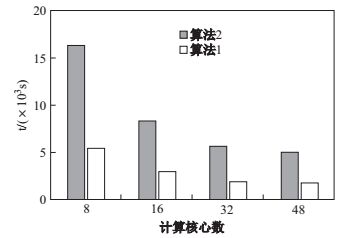
然后, 我们对90万行数据, 不同计算核心, 隐变量模型包括7个节点(其中2个隐变量)的情况下, 算法1和算法2的执行时间进行了对比.如图 13所示, 算法2的执行时间远高于算法1, 随着计算核心的增多, 算法1和算法2的执行时间都有明显减少, 这从一定程度上说明本文方法具有较好的可扩展性.
|
图 13 执行时间对比 Fig.13 Comparison of execution time |
BN的推理是用BN的结构和参数来计算条件概率
| $\begin{align} Pre=\dfrac{num(ture)}{num(inference)}. \end{align}$ | (7) |
| $\begin{align} Cov=\dfrac{num(ture)}{num(sample)}. \end{align}$ | (8) |
| $\begin{align} F=\dfrac{2\times Pre \times Cov}{num(sample)}. \end{align}$ | (9) |
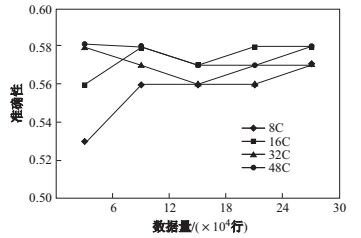
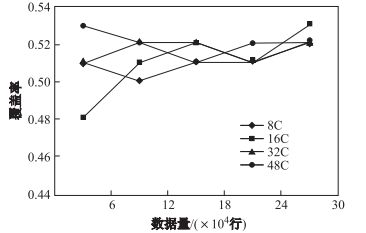
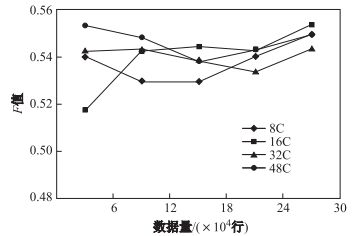
如图 14、图 15和图 16所示, 随着数据量的增大, 准确性、覆盖率以及
|
图 14 准确性 Fig.14 Precision |
|
图 15 覆盖率 Fig.15 Coverage |
|
图 16 F值 Fig.16 F score |
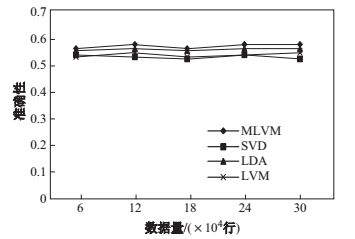
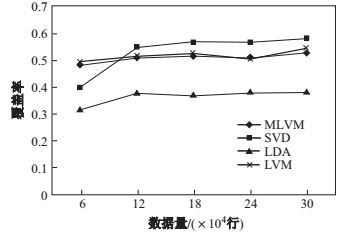
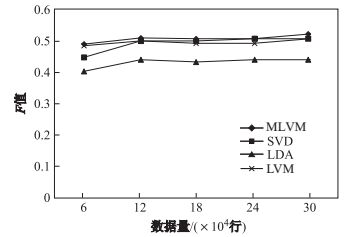
进一步对本文提出的模型(MLVM)与只含单隐变量的隐变量模型(LVM)、SVD和LDA的准确性、覆盖率和
|
图 17 准确性对比 Fig.17 Comparison of precision |
|
图 18 覆盖率对比 Fig.18 Comparison of coverage |
|
图 19 F值对比 Fig.19 Comparison of F scores |
本文从用户评分数据出发, 分析并描述了多维用户偏好, 以多个隐变量描述用户的多维偏好, 以含有多个隐变量的贝叶斯网来构建多维偏好模型, 并使用Spark计算框架实现模型构建方法, 建立在真实数据上的实验验证了本方法的效率和有效性.本文的模型既可以表达多个维度的用户偏好, 又可以描述用户评分数据中各属性间任意的依赖关系, 为后续的个性化等服务提供了更加准确的保证.
本文方法构建的多维偏好模型, 能够描述多个维度的用户偏好以及评分数据各属性间不确定的依赖关系.但是, 本文方法只能在静态数据上进行建模, 评分数据是动态变化的, 以增量的方式构建偏好模型仍需进一步探索.同时, 用户偏好也是动态变化的, 建立动态模型描述, 对变化的偏好进行估计, 是我们将要开展的研究工作.
| [1] | GROUPLENS RESEARCH.MovieLensDataset[EB/OL].[2017-08-20]. http://grouplens.org/datasets/movielens/. |
| [2] | KASSAK O, KOMPAN M, BIELIKOVA M. User preference modeling by global and individual weights for personalized recommendation[J]. Acta Polytechnica Hungarica, 2015, 12(8): 27-41. |
| [3] | YIN H, CUI B, CHEN L, et al. Modeling location-based user rating profiles for personalized recommendation[J]. ACM Transactions on Knowledge Discovery from Data, 2015, 9(3): 1-41. |
| [4] | YUAN Q, CONG G, MA Z, et al. Who, where, when and what:Discover spatio-temporal topics for Twitter users[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2013:605-613. |
| [5] | ZHAO K, CONG G, YUAN Q, et al. SAR:A sentiment-aspect-region model for user preference analysis in geo-tagged reviews[C]//IEEE, International Conference on Data Engineering. IEEE, 2015:675-686. |
| [6] | JIANG B, LIANG J, SHA Y, et al. Retweetingbehavior prediction based on one-class collaborative filtering in social networks[C]//Proceedings of the 39th International ACM Special Interest Group on Information Retrievalconference on Research and Development in Information Retrieval. ACM, 2016:977-980. |
| [7] | 张连文, 郭海鹏. 贝叶斯网引论[M]. 北京: 科学出版社, 2006. |
| [8] | DAPHNEKOLLER, NIRFRIEDMAN, 科勒, 等. 概率图模型[M]. 北京: 清华大学出版社, 2015. |
| [9] | KIM J S, JUN C H. Ranking evaluation of institutions based on a Bayesian network having a latent variable[J]. Knowledge-Based Systems, 2013, 50: 87-99. DOI:10.1016/j.knosys.2013.05.010 |
| [10] | SCHÜTZ W, SCHÄFER R. Bayesian networks for estimating the user's interests in the context of a configuration task[C]//Proceedings of the UM2001 Workshop on Machine Learning for User Modeling, 2001:13-17. |
| [11] | FRIEDMAN N. The Bayesian structural EM algorithm[C]//Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence, 2013:129-138. |
| [12] | ELIDAN G, FRIEDMAN N. Learning hidden variable networks:The information bottleneck approach[J]. Journal of Machine Learning Research, 2005, 6(6): 81-127. |
| [13] | JIN C, ZHANG Y, BALAKRISHNAN S, et al. Local maxima in the likelihood of gaussian mixture models:Structural results and algorithmic consequences[J]. Advances in Neural Information Processing Systems, 2016, 4(1): 16-24. |
| [14] | ZHAO G, QIANX, XIE X. User-service rating prediction by exploring social users' rating behaviors[J]. IEEE Transactions on Multimedia, 2016, 18(3): 496-506. DOI:10.1109/TMM.2016.2515362 |
| [15] | 高全力, 高岭, 杨建锋, 等. 上下文感知推荐系统中基于用户认知行为的偏好获取方法[J]. 计算机学报, 2015(9): 1767-1776. DOI:10.11897/SP.J.1016.2015.01767 |
| [16] | 王红兵, 孙文龙, 王华兰. Web服务选择中偏好不确定问题的研究[J]. 计算机学报, 2013, 36(2): 275-285. |
| [17] | 史艳翠, 孟祥武, 张玉洁, 等. 一种上下文移动用户偏好自适应学习方法[J]. 软件学报, 2012, 23(10): 2533-2549. |
| [18] | GAO R, YUE K, WU H, et al. Modeling user preference from rating data based on the bayesian network with a latent variable[C]//Proceedings of 17th International Conference on Web-Age Information Management, 2016:3-16. |
| [19] | HUANG Y, BIAN L. A Bayesian network and analytic hierarchy process based personalized recommendations for tourist attractions over the Internet[J]. Expert Systems with Applications, 2009, 36(1): 933-943. DOI:10.1016/j.eswa.2007.10.019 |
| [20] | CHAPELLE O, ZHANG Y. A dynamic Bayesian network click model for web search ranking[C]//Proceedings of the 18th International Conference on World Wide Web, ACM, 2009:1-10. |
| [21] | HUETE J, DE CAMPOS L M, FERNANDEZ-LUNA J M, et al. Using structural content information for learning user profiles[C]//Proceedings of 30th Special Interest Group on Information Retrieval, 2007:38-45. |
| [22] | AUFFENBERG F, STEIN S, ROGERS A. A personalised thermal comfort model using a Bayesian network[C]//Proceedings of the 2015 International Joint Conference on Artificial Intelligence, 2015:130-139. |
| [23] | YUE K, FANG Q, WANG X, et al. A parallel and incremental approach for data-intensive learning of Bayesian networks[J]. IEEE Transactions on Cybernetics, 2015, 45(12): 2890-2909. DOI:10.1109/TCYB.2015.2388791 |
| [24] | TAMADA Y, IMOTO S, MIYANO S. Parallel algorithm for learning optimal Bayesian network structure[J]. Journal of Machine Learning Research, 2011, 12(7): 2437-2459. |
| [25] | MIT. FullBNT[CP/OL].[2017-08-20]. http://www.cs.ubc.ca/murphyk/Software/BNT/FullBNT-1.0.4.Zip. |




