电子商务的发展, 使得协同过滤推荐迅速应用于信息过滤和信息推荐系统中, 并成为该领域的研究热点, 主要根据用户的相似性来产生推荐[1].随着电子商务服务范围的扩大, 项目评分的维度急剧增大且用户历史数据呈极端稀疏性.基于此, 研究者提出了大量的解决方案, 像基于关联规则、神经网络[2]、聚类[3]、贝叶斯网络[4]、时序[5]基于用户相似度的推荐; 基于标签[6-7]、分类[8], 但是, 这些研究均基于用户之间的相似度作推荐, 没有考虑商品性价比问题, 同时, 也没有考虑用户恶意评分给推荐准确度带来的影响.因此, 如何排除用户恶意评分影响, 尽量向目标用户推荐符合其兴趣的高性价比商品成为电子商务市场亟待解决的问题之一.
基于此, 本文提出一种基于复杂属性商品的混合协同过滤推荐模型, 该模型通过情景分类解决用户数据的极度稀疏性, 综合考虑用户对商品的属性评分和商品属性客观评分, 在尽量体现用户偏好的基础上克服网络水军的恶意评分, 同时模型通过社会网络理论和专家意见来克服传统计算用户相似度不能向用户推荐高性价比商品的弊端.
1 传统协同过滤推荐算法 1.1 传统协同过滤推荐算法描述协同过滤推荐是目前应用比较广, 研究比较多的算法之一, 也被称为社会过滤, 其基本思想认为:具有相似兴趣、爱好的用户, 也具有相似的信息、商品需求.主要分为基于用户和基于项目两类.前者认为若两个用户的爱好相似, 则其目标评分也应该相似, 后者认为用户过去喜欢的商品和现在喜欢的商品类似.
因此, 其通过计算用户或商品评分之间的相似性, 寻找最近邻居, 然后综合邻居评分得到预测评分, 进而为目标用户提供推荐, 其推荐的个性化程度比较高.也正是因为如此, 协同过滤从用户浏览、购买、评分等历史信息中分析用户的偏好, 不需要用户的直接输入, 减少了用户的负担.
其最近邻的选择主要有余弦相似度和修正的余弦相似度两类.设评分项目集合由
| $\begin{align} \label{eq1} &\mathrm {Sim}(i, j)=\cos (I, J)=\frac{I\times J}{\left\| I \right\|\times \left\| J \right\|}=\frac{\sum\limits_{c=1}^n {R_{i, c} R_{j, c} } }{\sqrt {\sum\limits_{c=1}^n {R_{i, c} ^2} } \sqrt {\sum\limits_{c=1}^n {R_{j, c} ^2} } }, \end{align}$ | (1) |
| $\begin{align} &\mathrm {Sim}(i, j)=\frac{\sum\limits_{c=1}^n {(R_{i, c} -\overline {R_i } )(R_{j, c} -\overline {R_j } )} }{\sqrt {\sum\limits_{c=1}^n {(R_{i, c} -\overline {R_i } )^2} } \sqrt {\sum\limits_{c=1}^n {(R_{j, c} -\overline {R_j } )^2} } }. \end{align}$ | (2) |
Lemire和Maclachlan于2005年提出了一种新的算法[9]——SlopeOne, 该算法的优点是计算复杂度低、精确率比较高, 不再基于相似性做预测, 而是利用线性回归模型做预测.该算法利用均值来代替未知项目之间的差异
| $\begin{equation} \mathrm {dev}_{i, j} =\sum\limits_{u\in U_{i, j} } {\frac{u_i -u_j }{\left| {U_{i, j} } \right|}}, \end{equation}$ | (3) |
其中,
在现实中, 商品属性繁多的商品往往是较为贵重的商品, 因此用户在购买之前往往会交流彼此的心得体会以及购物经验, 这种经验交流往往会对目标用户商品的选择, 产生直接或间接的影响[10], 然而传统的协同过滤往往是过于强调用户间兴趣的相似性, 而忽视了用户特征以及商品属性对用户选择的影响.
为解决该问题, Yuan等[11]和Ding等[12]认为社会网络可以用来描述用户间的交互行为; 邓晓懿等[13]提出了基于情境聚类和用户评级的协同过滤推荐模型, 通过引入情境因素和用户评级有效地解决了数据稀疏性和评分数据高维化的问题; Ma等[14]提出了一种结合项目评分和用户评分的混合推荐算法来缓解矩阵的稀疏性.
尽管这些研究其结果性能均优于传统的协同过滤算法.但是, 由于基于用户的协同过滤算法仅仅是根据用户相似度进行推荐的, 就比较容易产生“特殊化”的问题, 也就是说, 仅仅是考虑了用户间的关系, 没有考虑用户评分的准确性, 即没有考虑用户是不是随意写的评分, 或者是不是“网络水军”.
2 推荐模型的建立针对以上问题, 本文在对情境因素进行分类的基础上, 提出了一个基于用户评级的协同过滤推荐算法, 模型基本框架如图 1所示.模型首先利用用户注册获得用户的爱好和部分情境信息, 构建用户爱好矩阵, 以解决协同过滤推荐算法所面临的冷启动问题; 其次利用情境信息和传统分类对用户爱好矩阵进行分类, 以减小计算量; 再次, 引入社会网络和建立评级模型以解决稀疏性问题并分析用户间的爱好关系, 找到相似性最高的
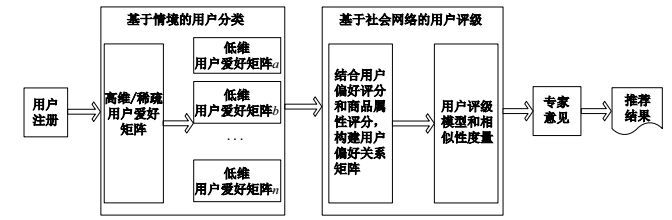
|
图 1 模型基本框架 Fig.1 The basic framework of the model |
本文将情境因素分为两种:用户情境和环境情境.用户情境包括用户的年龄、职业和性别, 用三元组表示, 如公式(4) 所示, 其中, 年龄集合分为6个年龄段, 即20岁以下、21--25岁、26--30岁、30--40岁、40--50岁、50岁以上; 性别集合由0和1构成, 分别代表男性和女性; 职业分为20种不同类型, 如工人、推销员、分析师、学生等等.具体公式为
| ${{E}_{u}}=\langle \text{Age},\text{Occupation},\text{Sex}\rangle ,$ | (4a) |
| $\text{Age}\in (A=\{{{A}_{i}}|i=1,2,\cdots ,6\}),$ | (4b) |
| $\text{Gender}\in (G=\{0,1\}),$ | (4c) |
| $\text{Occupation}\in (O=\{{{O}_{i}}|i=1,2,3,\cdots ,20\}).$ | (4d) |
环境情境则包括价格、目的、地点、时间等4种属性, 如公式(5) 所示, 具体类别则需根据实际数据进行量化.最后, 根据情境因素将用户划分为不同类别, 以使相同类别内用户具有较高相似度.具体公式为
| $\begin{align*} E_c =\langle\mathrm {Price,Des,Address,Time}\rangle, \end{align*}$ | (5a) |
| $\begin{align*} \mathrm {Price}\in {(P=\{P}_i {\vert i=1,2,\cdots,8\})}, \end{align*}$ | (5b) |
| $\begin{align*} & {\mathrm {Des}\in (D=\{D_i \vert i=1,2,\cdots,10\})}, \end{align*}$ | (5c) |
| $\begin{align*} &{\mathrm {Address}\in (G=\{1,2,3,\cdots,27\})}, \end{align*}$ | (5d) |
| $\begin{align*} &{\mathrm {Time}\in (T=\{T_i \vert i=0,1,2,\cdots,5\})}. \end{align*}$ | (5e) |
首先, 根据用户评分数据和该商品客观评分数据构建用户、商品矩阵, 用以描述用户、商品之间的关系, 并作为数据预处理的基础矩阵; 其中, 客观评分来自于所有购买客户的综合评价所得, 能够比较真实地反映商品的各个属性.
设用户集合为
| 表 1 用户、商品矩阵 Tab.1 User-item matrix |
其次, 通过一个权值
| $\begin{equation} \label{eq5} i_j =\alpha \times ui_j +(1-\alpha )\times ci_j ,\quad j=1,2,\cdots,8. \end{equation}$ | (6) |
在实际购买商品时, 可能某一个单纯的偏好, 就能使用户决心购买某件产品, 其他的偏好作用并不大, 本文暂时称之为“孤立偏好”.为此, 根据目标用户偏好评分对偏好进行排序, 排序后, 删除偏好顺序和目标用户不一致的用户, 排序后为矩阵
| 表 2 用户、偏好客观评分排序矩阵 Tab.2 User, preference objective scoring matrix |
| 表 3 用户偏好关系矩阵 Tab.3 User, preference objective scoring presort matrix |
| 表 4 用户偏好关系矩阵 Tab.4 User, preferencerelation matrix |
| $\begin{equation} \label{eq6} U_4 =(u_{ij} )_{3\times 3} =U_3 \cdot U_3' ,\quad u_{ij} =\left\{ {\begin{array}{l} u_{ji}, \quad \mbox{如果}\;u_j \mbox{和}\;u_i \mbox{有相同的偏好}, \\ 0,\quad \;\;\;\mbox{如果}\;u_j \mbox{和}\;u_i \mbox{没有相同的偏好}. \\ \end{array}} \right. \end{equation}$ | (7) |
因此, 本文在矩阵
| $\begin{equation} \label{eq7} U_5 =(w_{ij} )_{m\times m}, w_{ij} =u_{ij} \Big/\sum\limits_{j=1}^m {u_{ij} }, \end{equation}$ | (8) |
这里
| $\begin{equation} \label{eq8} \sum\limits_{j=1}^m {w_{ij} =1, \;j=1, 2, \cdots, m}. \end{equation}$ | (9) |
如表 5所示, 可以发现
| 表 5 标准化用户偏好关系矩阵 Tab.5 Standared user, preference relation matrix |
在得到标准化偏好用户关系矩阵
由于用户偏好关系图
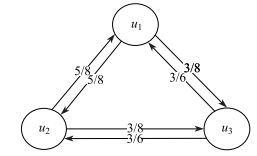
|
图 2 用户偏好关系图 Fig.2 The figure of user preference relation |
社会网络理论认为, 不同用户彼此相互影响, 用户偏好具有一定的传递性[16], 并且与PageRank模型中值的传递一样具有相同的衰减性[15].根据Arasu等对PageRank的定义[15], 定义公式
| $\begin{equation} \label{eq9} UR(u_i )=d\;\, \times \sum\limits_{u_j \in B(u_i )} {UR(u_j )/\mathrm {Outweight}(u_j )+(1-d)/m}. \end{equation}$ | (10) |
设
因为所有节点的PageRank的初始值都是未知的, 所以我们以均值作为其初始值, 即1/
在上一节, 已经求出目标用户偏好的最近邻集合, 根据传统的协同过滤推荐算法, 需要利用相似度最高的用户的评分为目标用户为评分项目预测评分.由于数据的稀疏性, 本算法不再对其进行预评分, 而是利用公式(3) 求出用户之间的相似性, 继而选择相似度最高的前
本文采用网上车市的网友评价及参数配置数据, 数据集通过自制爬虫程序获得, 包括13个级别及每个级别关注度排名前10的汽车品牌参数信息, 以及6 320条网友信息数据.网友信息包含两部分:情境信息和用户评分信息.情境信息包括购买车系、裸车购买价、购买时间、购买地点、购车目的, 由于数据总量较少, 本实验仅采用价格和购车目的作为情境因素.用户评分信息和汽车客观评分信息一样, 包括空间、动力、操作、油耗、舒适性、外观、内饰、性价比, 用户评分分值为1-5, 分值越高, 表示用户越满意.
专家意见主要考虑发动机性能和整车性能, 发动机性能暂定为, 排量相同情况下, 油耗越低越好; 整车质量根据厂家给的保修规则来判定, 保修年限或里程越长, 则认为其质量越可靠.
3.2 评判指标算法性能从两方面进行检验, 一方面将基于准确率进行评价, 因为只有分类准确度可用于分类问题中; 另一方面利用传统的平均绝对误差(Mean Absolute Error, MAE)来衡量用户预测评分和真实评分之间的差异.
分类准确度适用于0--1系统, 即用户对该项目喜欢还是不喜欢、推荐结果是否正确, 将预测过程假想为用户做决策的过程.本文使用精确度(Precision)衡量, 公式为
| $\begin{equation} \label{eq10} \mathrm {Precision}=\frac{\sum\limits_u {R_u \cap T_u } }{\sum\limits_u {\left| {R_u } \right|} }, \end{equation}$ | (11) |
其中,
评分绝对误差用MAE计算, 公式为
| $\begin{equation} \label{eq11} M_\mathrm{MAE} =\frac{\sum\nolimits_{i=1}^\mathrm {num} {\sum\nolimits_{j=1}^k {\left| {p_{ij} -q_{ij} } \right|} } }{\mathrm {num}\times k}, \end{equation}$ | (12) |
其中,
作为对比, 本文选取常用的基于用户的协同过滤推荐, 即利用目标用户注册的偏好信息和其余用户偏好评分信息, 一起构建用户项目评分矩阵, 找目标用户最相似的车型, 然后根据最终推荐车型信息和评分, 将其最终结果和本算法推荐的结果分别计算Precision和MAE.如图 3、图 4所示, 结果通过计算10名目标用户的均值得出, 横坐标表示用户数量的多少, 竖坐标分别表示Precision和MAE.
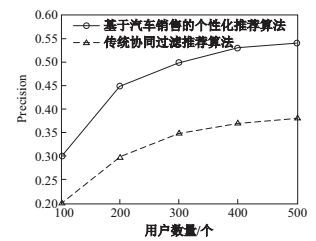
|
图 3 精确度 Fig.3 Precision |
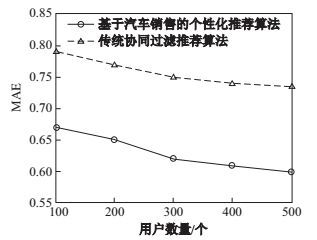
|
图 4 平均绝对误差 Fig.4 Mean absolute error |
图 3中, 可以看出, 随着用户偏好评分数量的增多, 两种推荐算法精确度都在逐渐上升, 但是基于汽车销售的个性化推荐, 算法始终表现出明显优势. 图 4中, 也可看出, 基于汽车销售的个性化推荐, 算法在评分上相比传统的协同过滤也要精确很多, 具有一定的优势.
4 结束语针对传统协同过滤算法应用于复杂属性商品推荐存在的问题, 提出一种基于复杂属性商品的混合协同过滤推荐模型, 通过结合用户主观评分和商品客观评分, 在尽量反映用户偏好的基础上得出一个混合评分, 并以此混合评分作为依据, 进行数据处理; 在提高推荐准确度方面, 通过专家意见提高商品性价比, 以此来提高用户的满意度.实验结果表明, 与传统协同过滤推荐相比, 该模型在平均绝对误差(MAE)和精确度(Precision)均具有较高优势.因此, 本模型相对传统协同过滤有效地提高了预测精度, 更适合于复杂商品属性推荐.未来的研究工作将结合社交网络进一步提高预测精度.
| [1] | 许海玲, 吴潇, 李晓东. 互联网推荐系统比较研究[J]. 软件学报, 2009, 20(2): 350-362. |
| [2] | 张锋, 常会友. 使用BP神经网络缓解协同过滤推荐算法的稀疏性问题[J]. 计算机研究与发展, 2006, 43(4): 667-672. |
| [3] | 王辉, 高利军, 王听忠. 个性化服务中基于用户聚类的协同过滤推荐[J]. 计算机应用, 2007, 27(5): 1225-1227. |
| [4] | ZIEGLER C N, MCNEE S, KONSTAN J, et al. Improving recommendation lists through topic diversification[C]//Proceedings of the 14th International World Wide Web Conference. 2005:22-32. |
| [5] | 陈曦, 成韵姿. 一种优化组合相似度的协同过滤推荐算法[J]. 计算机工程与科学, 2017, 39(1): 180-187. |
| [6] | 郭彩云, 王会进. 改进的基于标签的协同过滤算法[J]. 计算机工程与应用, 2016, 52(8): 56-61. |
| [7] | 宋伟伟, 杨德刚, 郑敏. 基于时间加权标签的协同过滤推荐算法研究[J]. 重庆师范大学学报(自然科学版), 2016, 33(5): 113-120. |
| [8] | 孙楠军, 刘天时. 基于项目分类和用户群体兴趣的协同过滤算法[J]. 计算机工程与应用, 2015, 51(10): 128-131. DOI:10.3778/j.issn.1002-8331.1405-0379 |
| [9] | LEMIRE D, MACLACHLAN A. Slope one predictors for online rating-based collaborative filtering[C]//Proceedings of the SIAM Data Mining (SDM'05). 2005:21-23. |
| [10] | LIU F, LEE H J. Use of social network information to enhance collaborative filtering performance[J]. Expert Systems with Applications, 2010, 37(7): 4772-4778. DOI:10.1016/j.eswa.2009.12.061 |
| [11] | YUAN W, GUAN D, LEE Y, et al. Improved trust-aware recommender system using small worldness of trust networks[J]. Knowledge Based Systems, 2010, 23(3): 232-238. DOI:10.1016/j.knosys.2009.12.004 |
| [12] | DING L, STEIL D, DIXON B, et al. A relation context oriented approach to identify strong ties in social networks[J]. Knowledge-Based Systems, 2011, 24(8): 1187-1195. DOI:10.1016/j.knosys.2011.05.006 |
| [13] | 邓晓懿, 金淳, 韩庆平, 等. 基于情境聚类和用户评级的协同过滤推荐模型[J]. 系统工程理论与实践, 2013, 33(11): 2945-2953. DOI:10.12011/1000-6788(2013)11-2945 |
| [14] | MA H, KING I, LYU M R. Effective missing data prediction for collaborative filtering[C]//Sigir Proceedings of Annual International ACM Sigir Conference on Research & Development 2007:39-46. |
| [15] | LI Y M, LAI C Y, CHEN C W. Discovering influencers for marketing in the blogosphere[J]. Information Sciences, 2011, 181(23): 5143-5157. DOI:10.1016/j.ins.2011.07.023 |
| [16] | YUAN W W, GUAN D H, LEE Y K, et al. Improved trust-aware recommender system using small-worldness of trust networks[J]. Knowledge Based Systems, 2010, 23(3): 232-238. DOI:10.1016/j.knosys.2009.12.004 |
| [17] | ARASU A, CHO J, GARCIA-MOLINA H, et al. Searching the Web[J]. ACM Transactions on Internet Technology, 2001(1): 2-43. |




