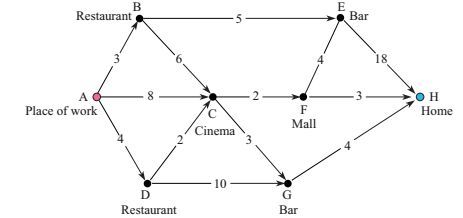
路径规划问题旨在图中寻找一条或多条从起点到终点并满足一定度量标准如长度、时间、代价或油耗等的最优路径, 已经在GPS导航、智慧交通、物流运输、无人机驾驶、旅游路线设计和通信路由等多个领域得到了广泛应用[1-6].传统的路径规划算法主要根据度量标准定义的边的权重来寻找具有最小权重和的路径作为最优路径, 除此之外现实生活中还存在大量对位置有多样性限制的路径规划需求.如图 1所示为一个道路交通网络的一部分, 每个点代表一个兴趣点(POI, Point of Interest), 表示该点所属的类别; 每条边表示兴趣点间的一条单向道路, 边上的数字表示该边的权重(这里为道路的长度).假设Tom结束了一天在A点的工作后, 想先去一家餐厅吃饭, 然后去电影院或酒吧放松一下(由于时间有限这二者只能择其一), 最后回到位于H点的家, 他希望规划一条满足上述位置限制要求的最短路径.
|
图 1 限制性路径问题的一个示例 Fig.1 An example of the constrained route planning problem |
日常生活中像这样对位置点和位置点类别有顺序、多选等限制的路径规划需求十分常见, 也已有一些研究工作关注:最优路径查询[7-13]搜索从查询点出发经过指定类别集合的最短路径, 主要关注位置点类别的无序、有序、部分有序等限制; 文献[14-16]查找从起点到终点, 途径指定关键词集合且满足行程预算的路径, 忽略了途径点的顺序限制, 加入关键词匹配度、路径流行度等考量因素更适于具体的应用场景.现有工作仅是研究限制性路径规划问题的子集或者特殊情况, 不能解决对位置点既有经过的顺序限制, 又有多选需求的路径规划.
鉴于此, 本文研究在图中搜索从给定起点到终点, 并对途径位置点和类别有顺序、多选等多重限制的最优路径问题.考虑到此类路径规划需求中富含多种语义信息, 引入正则表达式来表达查询.正则表达式是表示字符串匹配模式的字符序列, 常用来检索或替换特定文本, 利用其已有的运算符定义可以表达路径规划查询中的多种限制, 且其解析后的有限自动机也可以辅助筛选符合条件的路径.首先, 本文形式化定义了基于正则表达式的限制性路径规划问题CRPP(Constrained Route Planning Problem); 接着结合自动机理论和Dijkstra最短路径算法, 提出了一个解决CRPP的通用框架; 在此基础上设计了一个基本的限制性路径规划算法BCRP(Basic Constrained Route Planning), 并通过加入剪枝策略提出了改进的限制性路径规划算法ICRP(Improved Constrained Route Planning), 减少了搜索空间并提升了处理性能.
本文的主要贡献如下.
(1) 提出并形式化定义了基于正则表达式的限制性路径规划问题, 即找到图中从指定起点到终点, 并满足个性化位置限制条件, 如顺序或无序经过给定位置点或类别集合的全集或子集的最短路径, 利用正则表达式完整准确地表达复杂的限制性路径查询;
(2) 设计了一个解决CRPP的通用框架, 并基于此框架提出了基础的和改进的限制性路径规划算法, 改进的限制性路径规划算法通过剪枝策略显著提升了时间和空间效率;
(3) 应用真实数据集的实验结果表明方法的可行性和高效性.
本文内容组织如下:第1节介绍相关工作, 第2节给出了问题的形式化定义, 第3节叙述了通用的解决框架, 在此框架的基础上第4节阐释了两种限制性路径规划算法BCRP和ICRP, 第5节介绍了实验及实验结果, 最后第6节总结了全文.
1 相关工作最优路径查询起源于最短路径问题, 由于考虑了多种限制性因素, 因此相比最短路径问题更有实际意义.李飞飞等[7]提出了在空间数据库中的路径规划查询TPQ (Trip Planning Query), 空间数据库中的每个空间对象有位置和类别信息, TPQ的目的是寻找从起点到终点, 经过给定点类别集合中每个类别至少一个空间对象的最短路径, 是广义旅行商问题的特例. TPQ中用户不能指定希望经过的类别顺序, 且文献[7]采用近邻搜索的思想给出问题的近似解. Sharifzadeh等人[8]研究的最优顺序路径查询OSR (Optimal Sequenced Route Query), 用来寻找从某一点开始, 严格按照指定顺序经过给定点类别集合中每个类别至少一个点的最短路径, 并给出了在欧式空间适用的LORD和R-LORD算法以及在路网中适用的PNE算法.文献[9-10]通过研究OSR问题空间的几何学性质, 基于泰森多边形对给定的类别顺序进行预处理, 构建了一系列AW-Voronoi Diagrams来有效解决OSR查询.文献[11]研究的通用最短路径问题本质上为指定终点且严格有序的OSR, 使用了动态规划的思想更适用于路网等大规模图中.不同于OSR定义点类别的全序, Chen等人[12]提出了一种多规则部分有序路径MRPSR (Multi-rule Partial Sequenced Route)查询, 只有部分有序的类别集合被定义.文献[13]解决从起点出发经过一个用户定义的类别集合的最优路径查询, 支持不同类别间的部分顺序限制.上述研究主要关注最短路径上位置点的类别特征, 仅支持对位置点类别及其经过顺序的限定, 不能对位置点和类别进行多选等要求.
文献[14]提出了一种多近似关键词路径MAKR (the Multi-Approximate-Keyword Routing)查询, 查询中不仅定义了起点和终点, 也定义了一组(关键词, 阈值)键值对, 旨在搜索从起点到终点, 至少经过每个关键词的一个空间对象的最短路径, 且该空间对象与此关键词的匹配度需高于指定阈值.关键词感知的最优路径查询KOR (Keyword-aware Optimal Route Query)[15-16]综合考虑了关键词覆盖条件、代价约束和路径流行度三方面因素, 查找从起点到终点, 经过指定关键词集合中的点同时满足行程预算且流行度最大的路径, 实现近似求解.上述针对关键词的路径查询中, 每个位置点关联一个或多个关键词, 本质上也可以转化为类别信息进行处理.不同的是, MAKR和KOR只考虑了需经过的点所属的关键词, 并没有考虑经过的顺序限制.而加入关键词匹配度、路径流行度等度量标准只适合包含这些特定信息的应用场景.
同样使用正则表达式的手段定义限制性路径问题, 文献[17]研究了形式化语言限制性最短路径问题.不同于本文考虑对位置点的限制, 文献[17]考虑的是对组成路径的边的限制, 即结果路径上边的标签需满足正则表达式.
通过分析发现现有研究工作主要集中于类别信息, 有些没有考虑顺序限制, 有些给出的是问题的近似解, 有些额外考虑了路径流行度等因素仅适用于具体场景的应用, 有些关注的是对路径上边的限制, 还没有工作考虑位置点及类别的多选需求.本文面向更加通用的限制性路径规划问题, 全面考虑了位置点和类别的经过顺序、多选等限制条件, 上述问题均可转化为本文定义的基于正则表达式的限制性路径规划问题加以解决.
2 问题定义定义1(图) 给定有向图
定义2 (限制性路径查询) 限制性路径查询
通过上述元素的排列组合, 限制性路径查询可以表达丰富的限制性路径规划需求.由于可以将一个位置点视为一个单独的类别, 因此位置点的处理可以转化为类别的处理, 下面仅以位置点类别为操作对象介绍限制性路径查询及其处理方法.
设正则表达式中第一个点为起点
值得注意的是, 闭包操作符
| $\begin{align} sc_i(c_j)^{\ast}t\Longrightarrow sc_it, \end{align}$ | (1) |
| $\begin{align} sc_i(c_j)^+t\Longrightarrow sc_ic_jt. \end{align}$ | (2) |
规则(1) 的含义是某一个位置点或类别出现零次或多次相当于对路径查询没有影响, 可以从查询中去掉; 规则(2) 的含义是某一个位置点或类别出现一次或多次可以根据最短路径性质化简为出现一次.由此下文对限制性路径查询的处理主要考虑其他3种符号操作.
在传统正则表达式和有限自动机理论中, 当且仅当字符串中的每个字符都在正则表达式中定义, 才会被该正则表达式生成的有限自动机接受.如只有“ACFI”或“ACGI”才能通过AC(F
定义3(限制性路径规划问题) 给定一个有向图
Tom的限制性路径规划问题即:在图 1所示的图中找到满足
针对上述限制性路径规划问题, 通过正则表达式表达的限制性路径查询, 结合Dijkstra最短路径算法, 本文提出了一个通用的查询处理框架.选择Dijkstra算法的原因在于: Dijkstra算法是最具代表性的求解非负带权图的最短路径算法, 程序设计简单, 通用性强, 是现有众多最短路径算法的基础, 方便扩展到其他最短路径算法上.本框架首先解析查询
NFA和DFA都用状态转移表表示, 给定状态和类别, 转移的结果为状态转移表中(状态, 类别)的值, 即下一个状态; 如果表中不存在对应的项, 该类别就不是针对当前状态的一个可转移类别.对查询

|
图 2 示例查询解析后的状态转移表 Fig.2 The state transition table |
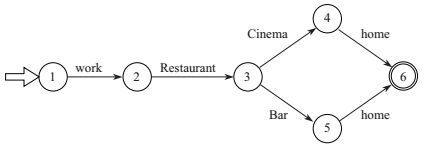
|
图 3 示例查询解析后的状态转移图 Fig.3 The state transition diagram |
因此可以通过状态转移表来检查路径是否符合限制性条件:当且仅当以该路径上点的顺序可以驱动有限自动机从初始状态到接受状态, 即终结状态, 那么这条路径是符合限制性路径查询的路径.
4 限制性路径规划算法在上节提出的查询处理框架的基础上, 本节介绍限制性路径规划算法, 包括基本算法BCRP和它的改进算法ICRP.
4.1 基本的限制性路径规划算法BCRPBCRP算法以类Dijkstra算法为主线来寻找最短路径, 同时用限制性路径查询解析后的状态转移表过滤不符合限制条件的路径.不直接使用Dijkstra算法的原因在于: Dijkstra算法中被标记为访问过的点不会在后续过程中被扩展, 因为被标记时对应的路径一定是从
在定义2中已经提到, 传统的正则表达式是字符串的完全匹配, 而CRPP中查询只包含用户关心的位置点或类别, 因而是一种部分匹配.对此, 定义一个额外的任意状态
| 算法1BCRP( |
| 输入:图 |
| 输出:图 |
| 1:获取 |
| 2:创建 |
| 3: while |
| 4: 取出 |
| 5: if |
| 6: return |
| 7: else |
| 8: BCRPGetLinks( |
| 9: end if |
| 10:end while |
| 算法 2 BCRPGetLinks( |
| 输入:图 |
| 1: for |
| 2: 创建 |
| 3: SetItemState( |
| 4: 将 |
| 5: end for |
| 算法3 SetItemState( |
| 输入:状态转移表 |
| 1: if |
| 2: |
| 3: if |
| 4: |
| 5: else |
| 6: |
| 7: end if |
| 8: else |
| 9: 与上述过程相同, 区别在于根据 |
| 10:end if |
为了更好地实现上述方法, 使用最短路径长度增序的优先级队列
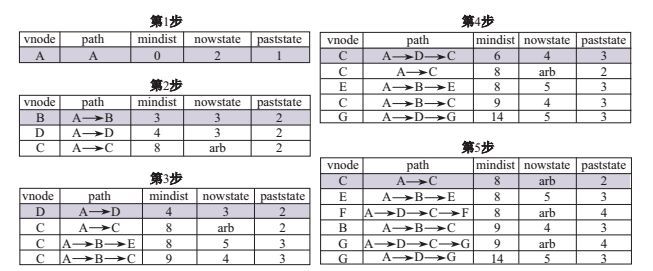
BCRP算法的执行过程可以通过优先级队列的变化过程表示. 图 4为BCRP算法针对图 1所示的限制性路径规划问题的前五步执行过程(深色元素表示此时的最短路径, 需在下一步被扩展).实际上BCRP相当于持续找下一条
通过分析发现在BCRP运行过程中有大量的冗余项, 即队列中已存在比该项更优的项被加入优先级队列.这不仅是对内存和计算资源的浪费, 更重要的是在后续的步骤中冗余项可能被扩展, 将导致持续的不必要的计算.如在图 4的第4步, 当考虑加入
剪枝策略 当考虑同一点
(1) 如果
(2) 如果
证明:由于两条路径的当前扩展结点均为
为实现上述剪枝策略, 除为所有点维护一个全局优先队列
| 算法4 ICRP( |
| 输入:图 |
|
输出:图 |
| 1:获取 |
| 2:将item |
| 3: while |
| 4: 取出 |
| 5: if item |
| 6: return item |
| 7: else |
| 8: if node |
| 9: 将node |
| 10: end if |
| 11: ICRPGetLinks( |
| 12:end if |
| 13: end while |
| 算法5 ICRPGetLinks( |
| 输入:图 |
| 1: for node |
| 2: 创建item |
| 3: SetItemState |
| 4: if |
| 5: 将item |
| 6: else if在 |
| 7: if item |
| 8: if item |
| 9: 将拥有更短mindist的项保留在 |
| 10: else |
| 11: 将item |
| 12: end if |
| 13: else |
| 14: 将拥有更短mindist的项保留在 |
| 15: end if |
| 16: else |
| 17: 将item |
| 18: end if |
| 19: end for |
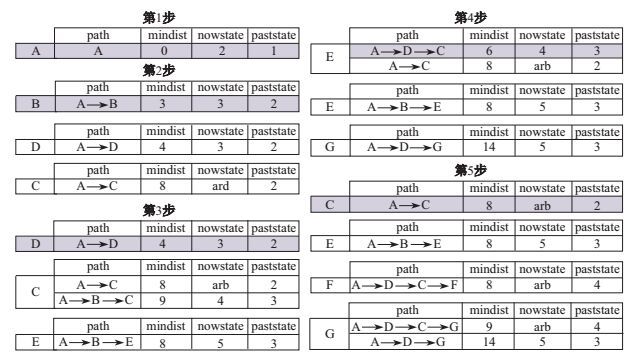
同样针对图 1中的例子, 图 5展示了ICRP算法运行过程的前五步.通过比较ICRP和BCRP的部分运行过程, 可以发现冗余项被排除.由于BCRP的正确性是显而易见的, ICRP通过使用剪枝策略减少了搜索空间, 只会提升算法效率而不会破坏算法的正确性, 因此ICRP的正确性也被证明.
5 实验与结果本节使用真实的路网数据进行实验.所有算法均由Java语言编程实现且运行在处理器为Intel Core i5-4460 3.20 GHz, 内存16 G, Windows操作系统的PC机上.
5.1 实验设置数据集 使用California真实路网数据[7] (21 048个点, 21 693条边), 为每个点随机分配一个正整数
查询 为不失查询的一般性, 设
表 1详细展示了实验的具体设置, 非特殊说明都采用默认值.
| 表 1 实验设置 Tab.1 Settings of experiments |
由于第4节中已经证明了算法的正确性, 因此在实验阶段主要关注算法的有效性, 体现在查询响应时间和扩展结点数目两个方面.查询响应时间代表算法的处理效率, 扩展结点数目表示有多少可能的路径被验证, 代表查询空间的规模.由于据我们所知尚没有相关工作解决与我们定义相同的限制性路径规划问题, 因此本文主要对BCRP和ICRP算法进行对比实验来考察剪枝策略对算法有效性和性能的影响.
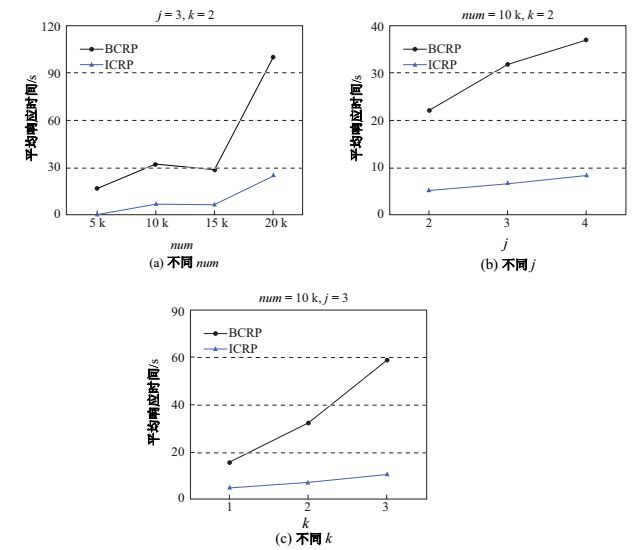
图G对算法的影响 通过抽取子图中点的数目num来考察
|
图 6 采用不同num, j, k时的平均响应时间 Fig.6 Average response time when varying num, j and k |
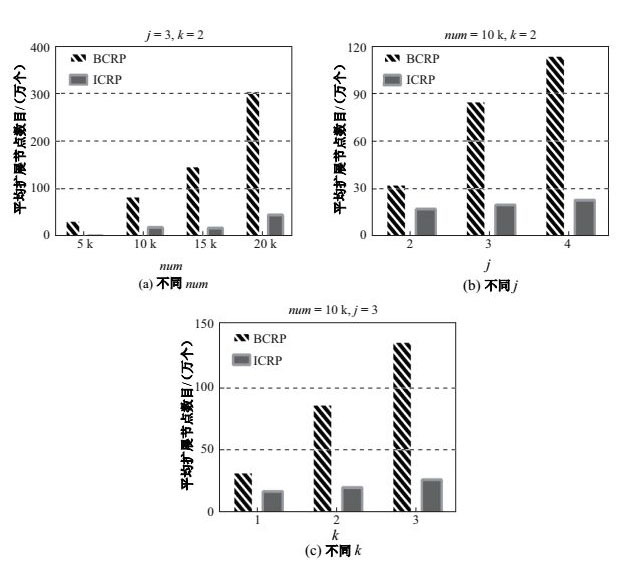
|
图 7 采用不同num, j, k时的平均扩展节点数目 Fig.7 Average number of expanded nodes when varying num, jand k |
限制性路径查询q对算法的影响
BCRP和ICRP算法的有效性分析假设运行时间超过3 min就是不可接受的, 在实验过程中发现, 只有在较小的图上进行较简单的查询时BCRP算法才可以运行出可以接受的结果, 如当num为5 k时, BCRP算法尚能获得较好的性能, 但是增加到10 k时, 查询的不可接受率几乎达到50%, 15 k时超过70%, 当
本文研究了限制性路径规划问题CRPP, 首先通过利用正则表达式表示限制性路径查询的方式形式化定义了该问题, 接着设计了一种解决的通用型框架, 然后提出了基本的限制性路径规划算法BCRP, 并在此基础上引入剪枝策略减少冗余路径和计算代价, 最后通过大量的实验分析表明本文的方法是可行且高效的.未来的工作主要包括提升现有算法在大规模图中的适用性.
| [1] | LIU H, JIN C, ZHOU A. Popular route planning with travel cost estimation[C]//Proceedings, Part Ⅱ, of the 21st International Conference on Database Systems for Advanced Applications. New York:Springer-Verlag, 2016, 9643:403-418. |
| [2] | YUAN J, ZHENG Y, ZHANG C, et al. T-drive:Driving directions based on taxi trajectories[C]//Sigspatial International Conference on Advances in Geographic Information Systems. New York:ACM, 2010:99-108. |
| [3] | ZHENG Y, CAPRA L, WOLFSON O, et al. Urban computing:Concepts, methodologies, and applications[J]. ACM Transactions on Intelligent Systems and Technology, 2014, 5(3): 38 |
| [4] | ZHANG S, QIN L, ZHENG Y, et al. Effective and efficient:Large-scale dynamic city express[J]. IEEE Transactions on Knowledge & Data Engineering, 2016, 28(12): 3203-3217. |
| [5] | LU H C, LIN C Y, TSENG V S. Trip-Mine:An efficient trip planning approach with travel time constraints[C]//IEEE International Conference on Mobile Data Management.[S.l.]:IEEE, 2011:152-161. |
| [6] | MALVIYA N, MADDEN S, BHATTACHARYA A. A continuous query system for dynamic route planning[C]//IEEE, International Conference on Data Engineering.[S.l.]:IEEE Computer Society, 2011:792-803. |
| [7] | LI F, CHENG D, HADJIELEFTHERIOU M, et al. On trip planning queries in spatial databases[J]. Journal of Combinatorial Optimization, 2005, 31(1): 1-16. |
| [8] | SHARIFZADEH M, KOLAHDOUZAN M, SHAHABI C. The optimal sequenced route query[J]. The VLDB Journal, 2008, 17(4): 765-787. DOI:10.1007/s00778-006-0038-6 |
| [9] | SHARIFZADEH M, SHAHABI C. Additively weighted voronoi diagrams for optimal sequenced route queries[J]. Workshop on Spatio-Temporal Database Management, 2006 |
| [10] | SHARIFZADEH M, SHAHABI C. Processing optimal sequenced route queries using voronoi diagrams[J]. Geoinformatica, 2008, 12(4): 411-433. DOI:10.1007/s10707-007-0034-z |
| [11] | RICE M N, TSOTRAS V J. Engineering generalized shortest path queries[C]//IEEE International Conference on Data Engineering.[S.l.]:IEEE Computer Society, 2013:949-960. |
| [12] | CHEN H, KU W S, SUN M T, et al. The multi-rule partial sequenced route query[C]//ACM Sigspatial International Symposium on Advances in Geographic Information Systems. USA:DBLP, 2008:1-10. |
| [13] | LI J, YANG Y, MAMOULIS N. Optimal route queries with arbitrary order constraints[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(5): 1097-1110. DOI:10.1109/TKDE.2012.36 |
| [14] | YAO B, TANG M, LI F. Multi-approximate-keyword routing in GIS data[C]//ACM Sigspatial International Conference on Advances in Geographic Information Systems. New York:ACM, 2011:201-210. |
| [15] | CAO X, CHEN L, CONG G, et al. Keyword-aware optimal route search[J]. Proceedings of the VLDB Endowment, 2012, 5(11): 1136-1147. DOI:10.14778/2350229 |
| [16] | CAO X, CHEN L, CONG G, et al. KORS:Keyword-aware optimal route search system[C]//IEEE, International Conference on Data Engineering.[S.l.]:IEEE, 2013:1340-1343. |
| [17] | BARRETT C, JACOB R, MARATHE M. Formal language constrained path problems[J]. Computing, 1998, 30(3): 234-245. |