纵观近十几年, 互联网的发展异常迅猛, 导致数据规模不断增加, 随之带来的问题是如何存储并快速分析海量数据.为了提高海量数据下的存储、查询和分析的处理速度, 产生了各种分布式架构的设计思想.无共享架构(Shared-Nothing Architecture)中每个节点具有私有的处理器、内存、磁盘等资源, 多个节点之间通过高速网络相互连接, 没有资源竞争, 容易通过添加节点来提高集群的存储能力和计算能力, 有非常高的扩展性和高并发的特点, 因此在OLAP (Online Analytical Processing)系统中应用越来越广泛[1].
Jim Gray, 作为数据库方向的开山鼻祖早在10年前就曾说过: “磁盘将成为过去时, 闪存和内存将成为主旋律.”在大数据处理的场景下, 内存计算已成为海量数据存储和分析的重要技术手段.而传统关系型数据库系统如MySQL、SQL Server、Oracle h等大部分都是基于磁盘存储, 在处理查询及优化很多考虑都是基于减少I/O (Input/Output)次数、增加索引等方面, 同时也没有考虑分布式环境下数据的存储、内存的使用、CPU利用率和网络传输率等因素的影响, 因此基于分布式环境下的优化方法逐渐受到各方面的重视.
Ginkgo系统是华东师范大学数据科学与工程学院自主研发的基于内存计算的分布式数据分析系统, 能够提供高性能的实时数据查询分析服务[2].与比较流行的NoSQL型内存数据库不同的是, Ginkgo属于关系型数据库, 支持SQL92标准, 可以直接运用于大多数基于SQL的系统. Ginkgo可运行在拥有较大内存的商业服务器上, 同时可以动态的进行扩展, 开发成本低, 维护简单. Ginkgo自主开发的分布式查询引擎, 支持弹性流水线框架, 可以通过调度计算资源的分配, 使得查询效率最大化.
连接(join)操作是关系型数据库系统中极为重要的数据操作符, 也是数据分析中最消耗CPU、内存等资源的操作.尤其是在海量数据分析的场景下, 怎样保证数据正确性与实时性是亟待解决的问题.连接操作主要分为内连接(inner join)和外连接(outer join)两种.外连接与内连接不同的地方在于没有匹配的值需要用空值(null)来代替, 同时不能直接舍弃.外连接在商业中运用非常广泛[3], 例如用户表与订单表进行外连接来查看没有进行过交易的用户, 学生表与成绩信息表进行外连接就可以看出哪些同学还没参加考试, 在证交所(Ginkgo承接项目)场景中, 查询某时间段内各个地区的交易情况等等.有很多研究针对内连接以及分布式环境下的内连接进行了优化, 但这些优化方法不能直接应用于外连接.例如, 一种很典型的优化方法是通过运用半连接(semi-join)技术, 仅仅传输符合连接条件的子集, 可以进一步减少广播表的代价.另外, 外连接的主要实际应用场景是小表与大表进行连接, 一些通用的优化方法并不能充分利用应用场景进行优化.例如, 在Ginkgo中采用的是基于重分片(repartition)的哈希连接(Hash join)算法[4], 在小表和大表做连接的场景下, 需要将小表加上大表所有的数据重新发送到对应新的节点上.然而实际上通过复制分片(duplication)的方法, 将小表广播到其他各个节点的代价会远小于重分片的方式.在过滤出小表的子集时, 一般的做法是将大表的某一列传输到对应的小表上进行筛选[5]; 而半连接优化会将整列传送到另一表, 并且增加了额外的连接操作.更好的做法是构建一个可以快速判断是否存在于集合的过滤器, 以进一步减少网络传输的代价, 同时避免额外的连接操作[6-7].
针对以上问题, 本文在Ginkgo系统中实现了基于布谷鸟过滤器(Cuckoo filter)的分布式外连接算法.该算法通过由右表构造布谷鸟过滤器, 对将要进行广播的左表进行过滤, 同时在连接的时候通过判断是否存在于布谷鸟过滤器中来判断是否生成空值.本文的贡献点主要在以下几个方面.
(1) 提供了一种提高外连接性能的优化方案.
(2) 运用并修改布谷鸟过滤器来提升外连接性能.
(3) 在Ginkgo系统中实现了该算法.
(4) 通过测试证明该算法的可以提高外连接的性能.
本文第1节主要介绍传统的外连接算法及相关优化技术; 第2节详细阐述基于布谷鸟过滤器分布式外连接算法的设计与实现方案; 第3节对算法性能进行分析; 第4节通过实验验证该算法的性能提升; 第5节是总结及展望.
1 相关工作传统的连接算法有很多种, 例如嵌套循环连接、哈希连接、归并排序连接等等.然而在分布式环境下, 传统算法需要在数据混洗中进行, 因此需要考虑包括网络传输带来的性能问题.本文所提出的外连接算法, 是在网络传输为瓶颈的条件下, 通过减少网络传输, 同时提高并行度, 来提高外连接性能.
1.1 哈希连接算法1979年Blasgen首次提出了通过哈希函数实现连接的算法[8].哈希连接主要分成两步:第一步扫描其中一张表的元组, 根据连接条件所在列构建哈希表, 此阶段被称为build阶段; 第二步, 将另一个表的元组逐个取出, 在哈希表中进行探测.若探测成功则会生成新的元组, 该阶段也被称作probe阶段.在多数情况下, 哈希连接算法优于其他连接算法(例如嵌套循环连接、排序归并连接等).
1.2 重分片分布式外连接算法在分布式数据库系统中, 关系或者关系的分片总是分布在不同的站点上, 当两个关系做连接时, 如果在无数据传输方式下得到正确结果, 则称两个关系在该连接条件下站点依赖[9].可见, 站点依赖有效利用了局部查询的本地化特征, 使得查询过程可以并发执行, 资源可以得到充分地利用, 最终提升性能.
而大多数的查询并不能满足站点依赖, 重分片分布式连接算法[10]则通过按照join条件所在列对原数据进行重分片使得两个表在连接条件下站点依赖.因此, 重分片分布式连接算法主要分两步:第一步, 如果两个表原始分片所依据的列不是连接条件所在的列, 则需要按照连接条件所在列进行数据重分片.例如, 假设有如图所示地两个关系
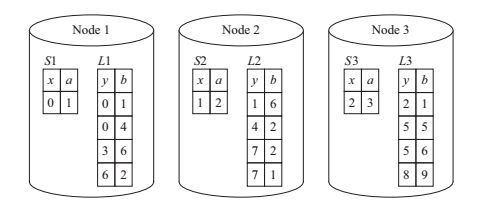
|
图 1 关系 |
| $\begin{array}{l} Select\;S.x,\;S.a,\;L.y\\ From\;S\;left\;outer\;join\;L\\ On\;S.a = L.b. \end{array}$ | (Q1) |
需要将关系
重分片分布式连接的性能虽然不受分片数量的影响, 但在有数据倾斜或两表数据量差异较大的情况下表现并不好.
1.3 复制分片分布式外连接算法复制分片分布式连接算法主要分为4步[11].第一步, 将表数据量比较小的表分片发送到其他各个节点上, 使得每一台机器上都由该小表的所有数据.这里使用第1.2节的示例, 图 2所示的结果就是将表
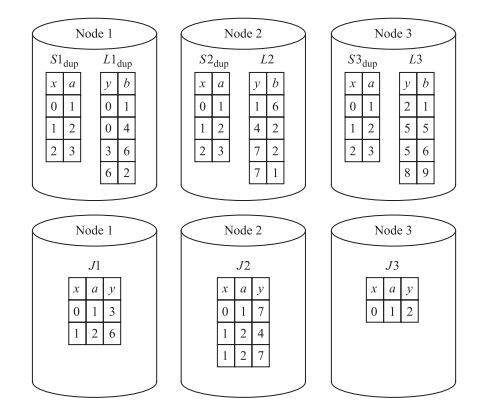
|
图 2 中文复制分片分布式连接算法的第一步和第二步:数据被复制到其他所有节点上, 并将 |
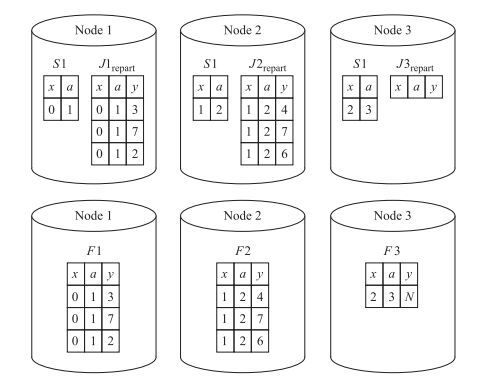
|
图 3 复制分片分布式连接算法的第三步和第四步:重分片中间结果 |
内连接的复制分片算法较外连接的简单很多, 只需要两步即可, 因为对于广播表
半连接(semi-join)操作是由投影和连接操作得到的一种关系代数操作.假设有
| $R{\infty _{A = B}}\left( {S{ \propto _{A = B}}\left( {{\Pi _A}R} \right)} \right),$ | (1) |
| $S{\infty _{A = B}}\left( {S{ \propto _{A = B}}\left( {{\Pi _B}S} \right)} \right).$ | (2) |
由以上关系代数可知半连接操作的大致过程如下:首先构造
但一般的半连接优化需要传输连接列的全部值, 且需要多做一次额外的连接.改进的半连接优化通过不同的构造投影集合的方式, 进一步减少传输代价.例如, 投影中有以下数据1, 2, 3, 99, 100, 1 000, 2 000, 3 000, 则可以构造[1, 100]和[1 000, 3 000]两个范围表达式.但这种方式很难确定范围表达式, 且过滤效果并不高[14].有研究提出在半连接优化中可以构造布隆过滤器, 提供快速的判断元素是否存在于集合内的数据结构, 减少额外的连接操作.但在外连接算法中, 必须精确判断元素是否存在于集合, 由于布隆过滤器存在假阳性(false positive), 会产生一些误报使得本不该在集合中出现的元组被判断为可以进行连接, 导致出错.因此布隆过滤器在外连接优化中并不适用.
针对以上问题, 本文根据Fan提出的布谷鸟过滤器(Cuckoo filter)[15]-----一种可以代替Bloom filter的数据结构, 与半连接优化的方式结合应用到分布式外连接算法中.
2 问题定义和算法设计及实现 2.1 问题定义设关系表
| $\begin{array}{l} Select\;S.x,\;S.a,\;L.y\\ From\;S\;left\;outer\;join\;L\\ On\;S.a = L.b. \end{array}$ | (Q1) |
算法在分布式环境下, 使用布谷鸟过滤器对复制分片的分布式外连接算法进行优化, 其核心思想是, 通过将连接列的去重集合构造成布谷鸟过滤器, 减少大表或中间结果的网络传输代价, 同时简化连接操作的复杂性, 提高并行度. Ginkgo的查询引擎是基于并行流水线的工作方式, 因此该算法能很好地运用于Ginkgo系统.
算法的流程如下.
(1) 在将各个计算节点上的
(2) 将构建好的过滤器广播到各台计算节点上.
(3) 将各个
(4) 在每个节点上并发地进行哈希外连接.若在探测阶段
在第(4) 步中, 之所以要再次判断是否满足所有的CF, 是因为, 如果能满足其中一个CF就说明该元组能在其他机器上连接成功, 因此不需要生成空元组.反之, 若不满足所有的CF, 则说明该元组没有连接成功的元组, 因此需要生成空值.
其流程图如图 4所示.
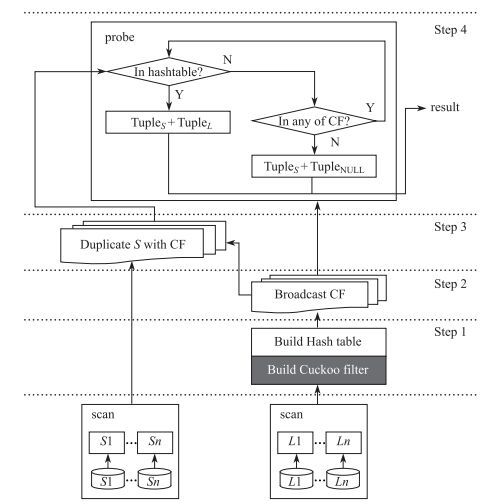
|
图 4 基于布谷鸟过滤器的分布式外连接算法流程图 Fig.4 The visual presentation of distributed outer join algorithm based on Cuckoo filter |
上文中提到布隆过滤器虽然空间利用率很高, 但由于布隆过滤器有一定的误报, 使得在第2.2节算法第(4) 步生成元组的时候有一定概率出错, 这在分析型数据库中是不能容忍的.为了解决这一问题, 本文引入布谷鸟过滤器(Cuckoo filter).
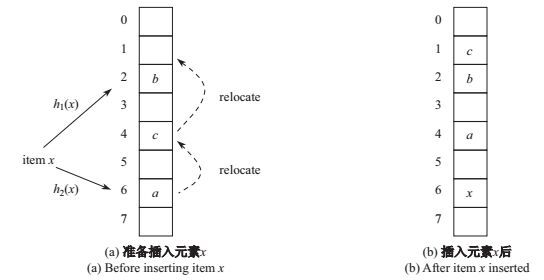
布谷鸟过滤器来源于Cuckoo Hashing算法[16], 原本是用来解决哈希冲突问题的一种方式, 通过这种方式生成的哈希表具有很高负载因子, 查询性能也非常高. Cuckoo Hashing的哈希函数是成对的, 元素通过两个哈希函数的计算会映射到两个位置, 可以理解成一个是记录位置, 一个是备用位置, 其中备用位置用来处理碰撞的.处理碰撞的方式也很简单, 若元素所对应的记录位置已经被占用了, 则将元素放置在备用位置; 若备用位置满了就随机从两个位置选出一个, 将该位置旧元素踢出, 将新元素插入.踢出的旧元素会查看自己另一个位置, 若为空则将自己放入, 若仍然被占用, 则重复上述操作直到不再发生替换或者达到预设替换次数上限. Cuckoo Hashing处理碰撞的方法与布谷鸟的幼鸟占据别的鸟类巢穴的做法相似, 因此得名.其流程图如图 5所示.
|
图 5 Cuckoo Hashing的流程图 Fig.5 Illustration of Cuckoo Hashing |
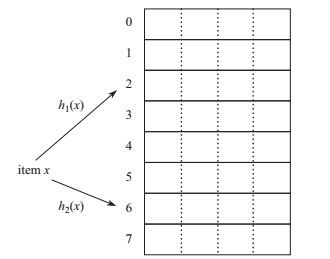
由Cuckoo Hashing的特性可知, 它适合大规模并发的读操作、少量写操作的场景. Bin Fan基于Cuckoo Hashing提出了布谷鸟过滤器, 他首先改进了其空间利用率, 初始Cuckoo Hashing的空间率最高在50%, 通过对每个桶增加槽位(slot)到4个, 使得在其他3路slot没被填满之前, 不会发生元素被踢出的情况, 这很大程度上缓冲了碰撞几率, 如图 6所示.
|
图 6 改进的多路布谷鸟过滤器 Fig.6 Improved Cuckoo filter with multi-slot |
Bin所设计的过滤器中存取的是原信息的指纹(finger print), 这样可以极大压缩原信息的占用空间, 但同时也会引入假阳性(false positive)的问题.增加指纹的位数可以降低误报的概率, 但同时会带来额外的存储空间, 因此这是一个需要权衡的问题.文献[15]中测试的平衡点是4路Slot12位的指纹, 当Cuckoo Hashing表中元素达到一定量的时候, 插入就很容易失败, 这时就需要扩展Hashing表来容纳更多的元素.但对于布隆过滤器来说, 插入元素多于一定值, 误报的概率会急剧上升, 导致基本失去作用.
如果将信息原值存入布谷鸟过滤器中则可以完全消除误报, 但需要牺牲一些额外的空间效率, 且存入整型元素对算法整体影响不高.由于存入重复数据时候每次都会到相同的哈希桶里进行插入, 这很容易造成插入失败, 因此本文在实现的时候限制了重复数据的插入.同布隆过滤器一样的是, 如何选择哈希函数会对布谷鸟过滤器性能产生很大的影响.本文采用Google提出的CityHash算法, 在保持高计算性能的前提下, 同时也保证了低碰撞率的特性.布谷鸟过滤器的构建算法见算法1.
| 算法1 布谷鸟过滤器构建算法 |
| Insert( 1 if filter. Contain( 2 return Done 3 4 5 6 if bucket [ 7 将 8 return Done 9 10 for 11 随机选取bucket[ 12 将 13 14 15 if bucket [ 16 将 17 return Done 18 运行至此说明布谷鸟过滤器满了, 需要重新分配新的空间 19 return Failure |
在算法第5步计算第二个桶的位置时, 使用第一个桶的位置与指纹的哈希值进行异或, 这样可以进一步分散两个桶的位置, 减少碰撞概率.在算法的第13步、第14步中, 由于考虑的是存储原值, 因此需要重新计算指纹信息, 得出第二个桶的位置.
当构建好过滤器之后, 需要通过布谷鸟过滤器对数据进行筛选, 筛选的查找算法见算法2.
| 算法2 布谷鸟过滤器查找算法 |
| Contain( 1 2 3 4 if bucket [ 5 return True 6 return False |
上面也曾提到, 布谷鸟过滤器适合高并发读的情况, 结合算法可知, 布谷鸟过滤器查找算法非常简单, 计算量也较布隆过滤器少.
3 算法分析 3.1 算法正确性分析该算法可以用公式
| $\begin{align} &R_i=(S_{\rm loc}\cup\sigma_{{\rm CF}(\Pi_{L.b}(L))}(S_{\rm others}))\bowtie_{S.a=L.b}(L_{\rm loc}) \\ &\qquad \cup S_{\rm loc}\propto_{S.a\neq L.b{\rm AND Not}{({\rm CF}(\Pi_{L.b}(L)))}}(L_{\rm loc}), \end{align}$ | (3) |
| $\begin{align} &S\propto_{L_{S.a=L.b}}=\cup^{n}_{i=0}R_i \end{align}$ | (4) |
推出.公式(3)、(4) 中
公式(3)
假设
基于传统的重分片外连接算法的网络传输开销
| $\begin{align} T_{\rm repart}&={\rm card}(S)\cdot {\rm size}(S)+{\rm card}(L)\cdot {\rm size}(L) \nonumber\\ &={\rm card}(S)\cdot ({\rm size}(S)+10{\rm size}(L)). \end{align}$ | (5) |
传统的重分片外连接算法网络传输代价主要由两个表分别做重分配组成.不受分片数量的影响, 比较稳定和通用.
基于传统的复制分片算法的网络传输开销主要来自两个阶段, 第一个阶段为广播
| $\begin{align} T_{\rm dup}=(p-1){\rm card}(S)\cdot {\rm size}(S)+q\cdot {\rm card}(S)\cdot {\rm card}(L)\cdot ({\rm size}(S)+{\rm size}(L)). \end{align}$ | (6) |
而基于布谷鸟过滤器的复制分片算法的网络传输开销主要由广播CF的时间加上广播
| $\begin{align} T_{\rm CF}&=q(p-1){\rm card}(S)\cdot {\rm size}(S)+k(p-1)\cdot {\rm card}(L)\cdot {\rm size}(L) \nonumber\\ &=q(p-1){\rm card}(S)\cdot {\rm size}(S)+10k(p-1)\cdot {\rm card}(S)\cdot {\rm size}(L), \end{align}$ | (7) |
其中
为了验证本算法的效率, 本文设计了两组实验, 从分片的数量和数据规模这两个方面, 观察相同查询语句的执行时间, 分析基于布谷鸟过滤器分布式外连接算法的性能.
4.1 实验环境实验采用Ginkgo1.0测试版进行实验.测试服务器基于CentOS release 6.5(Final)系统, CPU型号为Intel
实验的数据集采用TPC-H基准数据集, 通过TPC-H数据生成器生成.所用来测试的语句也是由TPC-H提供的Benchmark中的Query13, 为
| $\begin{array}{l} Select\;count\left( * \right)\\ From\;customer\;left\;outer\;join\;orders\\ On\;C\_custkey = O\_custkey{\rm{.}} \end{array}$ | (Q2) |
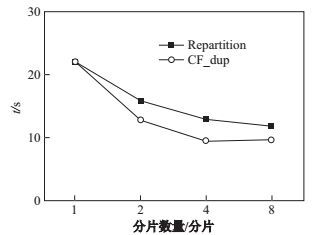
第一次实验选用TPC-H中SF10数据集, 即数据规模为10 GB, 其中左表约150万条元组, 右表约有1 500万条元组.分别将数据分成1, 2, 4, 8个分片(partition).实验结果如图 7, 其中横轴为分片数量, 纵轴为执行时间
|
图 7 基于布谷鸟过滤器复制分片外连接算法与哈希重分片外连接算法比较 Fig.7 Compare between duplication outer join algorithm based on Cuckoo filter and Hash repartition outer join algorithm |
从实验结果可以看出, 在1个数据分片时, 由于没有网络传输, 两种算法差异不大.在分片数增加时, 由于重分片外连接算法需要将两个表的所有数据都进行传输, 性能较布谷鸟过滤的复制分片算法来得差.当分片增多时, 由于计算资源的增加, 查询时间进一步减少.但当分片数量进一步增加时, 算法效率有所下降.这时因为复制分片算法的网络传输代价与分片数量成正比.当复制分片的代价总量与传输两个表所有数据的代价相当时, 该算法便会失去效果.
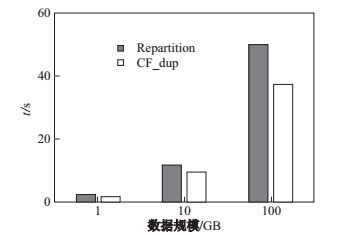
第二次试验分别选用TPC-H中1 GB, 10 GB, 100 GB的数据进行测试, 统一数据为8个分片.实验结果如图 8, 其中横轴为数据规模, 纵轴为执行时间
|
图 8 基于布谷鸟过滤器复制分片外连接算法与哈希重分片外连接算法比较 Fig.8 Compare between duplication outer join algorithm based on Cuckoo filter and Hash repartition outer join algorithm |
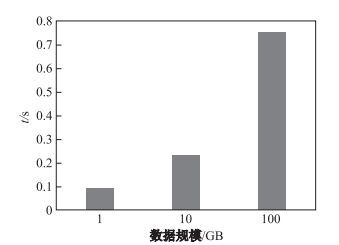
从实验结果得知, 当数据量增大时, 基于布谷鸟过滤器的复制分片算法的性能较好.这时因为当数据量增大时, 重分片所需要的网络传输量非常大.而复制分片只广播较小表的一部分和一个过滤器, 网络代价大大降低. 图 9即是传输布谷鸟过滤器的网络代价, 其中横轴为数据规模, 纵轴为执行时间.
|
图 9 基于布谷鸟过滤器复制分片外连接算法广播布谷鸟过滤器的代价 Fig.9 The costs of broadcasting Cuckoo filter in duplication outer join algorithm based on Cuckoo filter |
本文实现了一种基于布谷鸟过滤器的分布式外连接算法, 并在开源分析型内存数据库Ginkgo上进行了验证.该算法充分利用了布谷鸟过滤器高空间利用率、高查询效率和能去除重复元素的特性, 通过利用半连接的思想优化复制分片的分布式外连接过程, 减少了分布式环境下的网络传输代价, 增加了执行效率, 降低了外连接算法的复杂度, 提高了并发性.
但本算法仍然有优化空间.首先可以考虑将各个表上的常用连接的列所构造的布谷鸟过滤器进行缓存, 这样可以不仅可以节省每次查询都需要重复构建CF的时间, 同时也消除了广播CF的消耗, 或者利用压缩算法将CF进行压缩也可以进一步减少传输时间.另外在多个连接条件下, 如何选择合适的列来构造CF也是值得探讨的问题.
| [1] | STONEBRAKER M. The case for shared nothing[J]. Database Engineering, 1986, 9: 4-9. |
| [2] | 王立. 分布式内存数据库系统的查询处理与优化[D]. 上海: 华东师范大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10269-1015348214.htm |
| [3] | 邹先霞, 贾维嘉, 潘久辉. 实化外连接视图的增量计算[J]. 系统工程与电子技术, 2011, 33(4): 938-942. |
| [4] | 张磊, 方祝和, 周敏奇, 等. 面向内存计算的连接算法[J]. 华东师范大学学报(自然科学版), 2014(5): 180-191. |
| [5] | BERNSTEIN P A, CHIU D-M W. Using semi-joins to solve relational queries[J]. Journal of the Association for Computing Machinery, 1981, 28(1): 25-40. DOI:10.1145/322234.322238 |
| [6] | 樊秋实, 周敏奇, 周傲英. 基线与增量数据分离架构下的分布式连接算法[J]. 计算机学报, 2016, 39(10): 2102-2113. DOI:10.11897/SP.J.1016.2016.02102 |
| [7] | 茅潇潇, 段惠超, 高明. OceanBase中基于布隆过滤器的连接算法[J]. 华东师范大学学报(自然科学版), 2016(5): 67-74. |
| [8] | BLASGEN M W, ESWARAN K P. Storage and access in relational data bases[J]. IBM Systems Journal, 1977, 16(4): 363-377. DOI:10.1147/sj.164.0363 |
| [9] | 赵宇兰. 分布式数据库查询优化研究[M]. 成都: 电子科技大学出版社, 2016. |
| [10] | LI J T, XIA X L. Research on outer join optimization in parallel DBMS[C]//Proceedings of the 2011 International Conference on Computer Science and Information Technology (ICCSIT 2011). 2011:502-507. |
| [11] | XU Y, KOSTAMAA P. A new algorithm for small-large table outer joins in parallel DBMS[C]//Proceedings of the IEEE 29th International Conference on Data Engineering (ICDE) (2010). IEEE, 2010:1018-1024. |
| [12] | CHENG L, KOTOULAS S, WARD T E, et al. Robust and efficient large-large table outer joins on distributed infrastructures[C]//European Conference on Parallel Processing. Berlin:Springer International Publishing, 2014:258-269. |
| [13] | XU Y, KOSTAMAA P, ZHOU X, et al. Handling data skew in parallel joins in shared-nothing systems[C]//Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. ACM, 2008:1043-1052. |
| [14] | CHENG L, KOTOULAS S, WARD T E, et al. Efficiently handling skew in outer joins on distributed systems[C]//Proceedings of the 14th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing. IEEE, 2014:295-304. |
| [15] | FAN B, ANDERSEN D G, KAMINSKY M, et al. Cuckoo Filter:Practically better than bloom[C]//Proceedings of the ACM International on Conference on Emerging Networking Experiments & Technologies. ACM, 2014:75-88. |
| [16] | PAGH R, RODLER F F. Cuckoo Hashing[J]. Journal of Algorithms, 2004, 51(2): 122-144. DOI:10.1016/j.jalgor.2003.12.002 |




