2. 重庆大学 电气工程学院, 重庆 408044;
3. 国家电网 重庆市电力公司市区供电分公司, 重庆 408040
2. School of Electrical Engineering, Chongqing University, Chongqing 408044, China;
3. State Grid Corporation, Chongqing Electric Power Company Urban Power Supply Branch of China, Chongqing 408040, China
电磁探测是地球物理勘探的重要手段之一, 广泛应用于油气资源探测、矿产勘查、考古研究、现代城市建设、隧道矿井安全预测以及水文地质灾害勘查等传统领域.本文通过分析频域电磁探测发射机拓扑结构, 设计了具有上升、下降沿均钳位, 且输出电流阶段连接恒流源的频域电磁探测发射电路, 对钳位电压源电容、恒流电感值也进行了设计, 能在感性负载 100
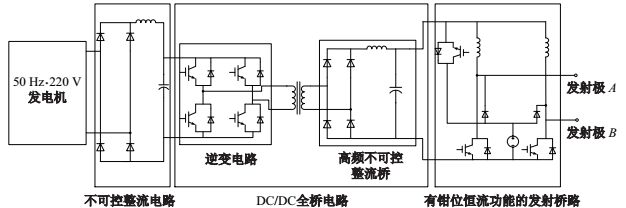
频域电磁(Frequency-domain Electromagnetic Method, FEM)探测发射机拓扑结构如图 1 所示. 供电电源为 50 Hz/220V 单相发电机, 经电感电容滤波的不可控整流电路之后, 接逆变电路与 DC/DC 全桥桥式电路, 再连接带有钳位电压源与恒流功能的交流方波发射桥路[1].
|
图 1 频域电磁探测发射机拓扑结构图 Fig.1 FEM transmitter topology |
频域电磁探测整流电源设计要求: 交流供电 50 Hz/220 V 单相交流发电机;直流输出电压 200 V; 发射电流幅值 50 A; 最大发射频率 30 kHz.
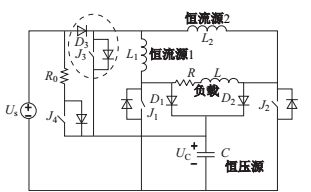
1.2 频域发射电路基本结构与原理频域发射主电路拓扑如图 2所示, 主要由恒流源单元、能量补充单元恒压钳位单元组成.恒流源单元在传统的全桥电路的基础上, 用电感
|
图 2 频域电磁法发射电路 Fig.2 FEM transmitting circuit |
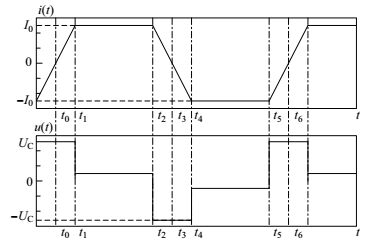
图 3 为理想的频域电磁探测发射电流电压波形.
|
图 3 理想频域电磁法发射电流电压波形 Fig.3 The ideal FEM transmitting current and voltage |
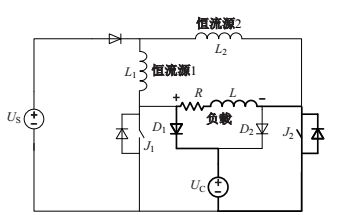
负载电流上升阶段工作情况如图 4 所示.
|
图 4 频域电磁法发射电流上升阶段 Fig.4 FEM transmitting circuit, rising-edge |
| $ i_0(t)=\frac{U_\mathrm C}{R_L}\big(1-\mathrm e^{-\frac{R_L}{L}(t-t_1) }\big), \quad t_0\leq t\leq t_1. $ | (1) |
令式(1) 为
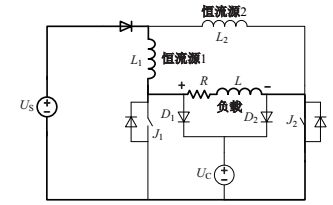
负载电流为正向恒定电流工作情况如图 5 所示.
|
图 5 频域电磁法发射电流正向恒定阶段 Fig.5 FEM transmitting circuit, positive current |
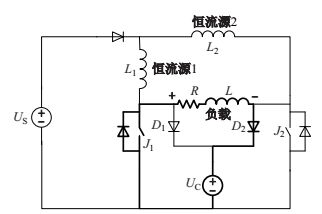
负载电流下降阶段工作情况图 6 所示.
|
图 6 频域电磁法发射电流下降阶段 Fig.6 FEM transmitting circuit, dropping-edge |
| $ i_0(t)=-\frac{U_\mathrm C}{R_L}+\Big(I_0+\frac{U_\mathrm C}{R_L}\Big)\mathrm e^{-\frac{R_L}{L}(t-t_2) }, \quad t_2\leq t\leq t_3. $ | (2) |
令式(2) 为 0, 则可求得下降沿时间
在频域发射电路中, 负载取值为
| $ L_1(L_2) >\frac{R_L}{f_{\max} \ln (\frac{R_LI-U_\mathrm S}{R_LI+R_L\Delta I-U_\mathrm S})}-L. $ | (3) |
考虑
考虑两个恒流电感电流低于设定值时, 能量全部由电容提供, 则钳位电压源给恒流电感充电阶段满足
| $ L\Delta I^2=\frac{1}{2}C\Delta U_\mathrm C^2. $ | (4) |
电流最大波动值为 0.5 A,
| $ C>\frac{2L\Delta I^2}{\Delta U_\mathrm C^2}. $ | (5) |
为了保证稳压效果,
为了确保系统的安全运行, 电阻
| $ R_0>(U_\mathrm C-U_\mathrm S)/I_{J_4}. $ | (6) |
额定工作电流
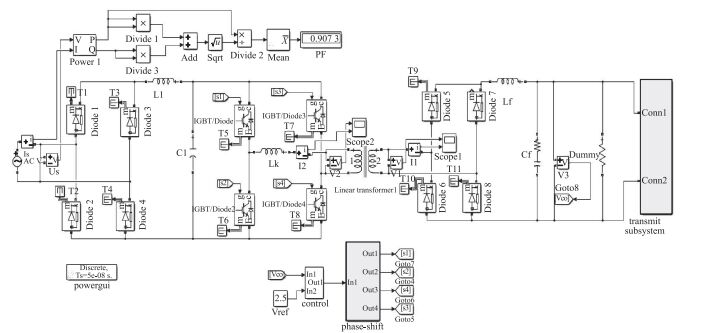
采用 MATLAB 进行仿真研究, 其中
|
图 7 时域电磁探测发射机系统闭环仿真电路 Fig.7 Close loop simulation of TDEM system |
发射子系统拓扑结构如图 8 所示. 在输出 10 kHz 到 30kHz 的交流方波为目标下, 以普通桥式电路的仿真结果与所采用发射电路的仿真结果做比较, 重点分析频域电磁探测发射电路的上升沿波形质量提升与恒流输出功能.
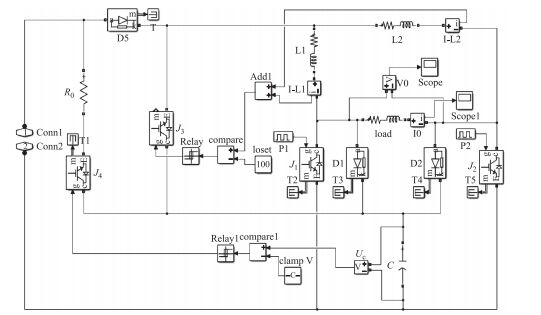
|
图 8 频域发射电路子系统 Fig.8 FEM transmitting subsystem |
频域电磁探测发射波形对于发射频率宽度的要求比时域探测宽得多, 为满足浅层探测, 频率通常会达到上千赫兹甚至上万赫兹, 所以发射波形的上升、下降沿的要求更为苛刻. 设置能通过的最大电流为25A, 并选取滞环环宽为 0.2 A.
发射频率为 10 kHz、20 kHz、30 kHz, 负载电阻为 4
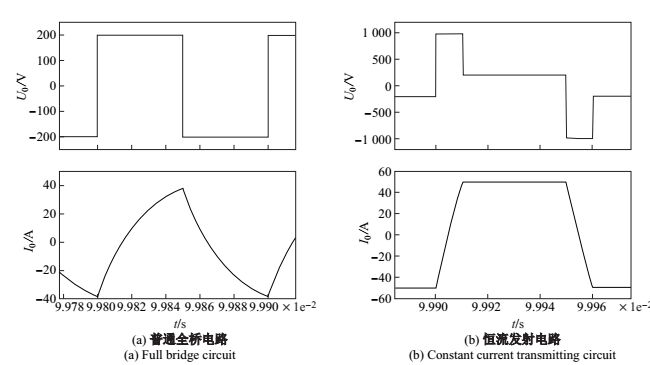
|
图 9 发射频率为 10 kHz 时负载电压和电流 Fig.9 Load voltage and current, 10 kHz |
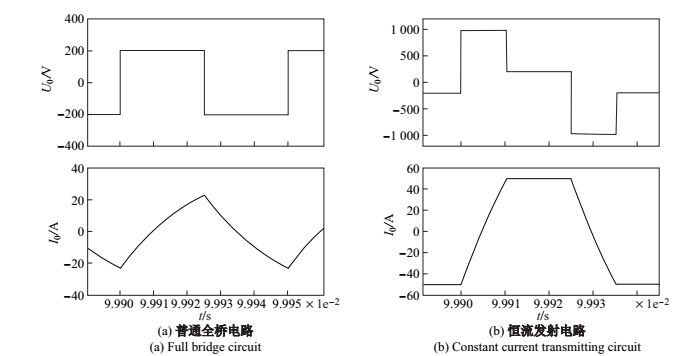
|
图 10 发射频率为 20 kHz 时负载电压和电流 Fig.10 Load voltage and current, 20 kHz |
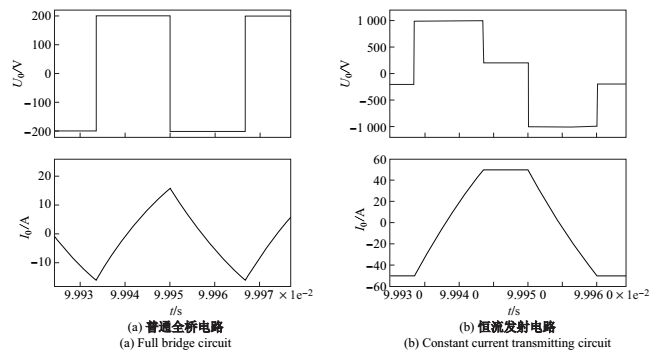
|
图 11 发射频率为 30 kHz 时负载电压和电流 Fig.11 Load voltage and current, 30 kHz |
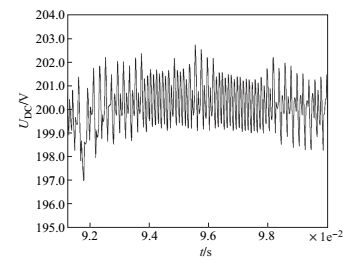
|
图 12 发射频率为 30 kHz, DC/DC 全桥变换电路输出电压放大图 Fig.12 30 kHz, output voltage of DC/DC full bridge converter |
从图 9、图 10、图 11、图 12 可知, 在电路参数相同的情况下, 常规全桥电路不能稳定地输出电流, 且输出完全由输入电压决定, 输出电流波形上升、下降沿缓慢, 无恒定电流输出阶段,
本文对频域电磁探测发射机系统进行分析与设计, 设计了具有上升、下降沿均钳位, 且输出电流阶段连接恒流源的频域电磁探测发射电路, 对钳位电压源电容、恒流电感值进行了设计, 能在感性负载 100
| [1] | 张丹丹, 胡建明, 崔婷, 等. 带传感器的射频识别技术在变电站电气设备状态信息采集中的应用[J]. 高电压技术, 2013, 39(11): 2623-2630. |
| [2] | 范佳兴, 李兵, 何怡刚, 等. ETC系统信道传播损耗评估方法研究[J]. 电子测量与仪器学报, 2015, 29(8): 1164-1170. |
| [3] | BOYER C, ROY S. Backscatter communication and RFID:Coding, energy, and MIMO analysis[J]. IEEE Transactions on Communications, 2014, 62(3): 770-785. DOI:10.1109/TCOMM.2013.120713.130417 |
| [4] | ARNITZ D, REYNOLDS M S. Multi-transmitter wireless power transfer optimization for backscatter RFID transponders[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12: 849-852. DOI:10.1109/LAWP.2013.2271984 |
| [5] | TROTTER M S, VALENTA C R, KOO G A, et al. Multi-antenna techniques for enabling passive RFID tags and sensors at microwave frequencies[C]//RFID, 2012 IEEE International Conference on. IEEE, 2012:1-7. |
| [6] | 李巨虎, 张海燕. 多天线UHF RFID系统的性能分析[J]. 华南理工大学学报, 2015, 43(5): 22-29. |
| [7] | CHEN H, WANG Z J. SER of orthogonal spacetime block codes over Rician and Nakagami-m RF backscattering channels[J]. IEEE Transaction on Vehicular Technolo-gy, 2014, 63(2): 654-663. DOI:10.1109/TVT.2013.2280598 |
| [8] | GRIFFIN J D, DURGIN G D. Link envelope correlation in the backscatter channel[J]. IEEE Communications Letters, 2007, 11(9): 735-737. DOI:10.1109/LCOMM.2007.070686 |
| [9] | 莫凌飞. 超高频射频识别抗金属标签研究[D]. 杭州: 浙江大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10335-2010067778.htm |
| [10] | 邬明罡, 李书芳. 金属对RFID系统影响研究[J]. 科学技术与工程, 2008, 18(8): 5242-5245. |
| [11] | 殷福荣, 王鹏飞, 刘芫健. 室内带金属家具环境的电波传播特性研究[J]. 中国电子科学研究院学报, 2014, 9(2): 209-216. |
| [12] | 甘雯雯. 地下隧道宽带无线信道传播特性的研究[D]. 北京: 北京交通大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10004-1014178207.htm |
| [13] | 邝向军. 关于金属介电常数的讨论[J]. 四川理工学院学报(自然科学版), 2006, 19(2): 75-78. |
| [14] | 佘开, 何怡刚, 朱彦卿, 等. MIMO-RFID系统反向识别距离研究[J]. 电子测量与仪器学报, 2012, 26(4): 305-311. |
| [15] | 庄铭杰. 计算机仿真无线Rice衰落信道的实现方法[J]. 电波科学学报, 2004, 19(5): 632-637. |
| [16] | 张秋艳, 黄海松, 陈伟兴, 等. 基于RFID技术的白酒物联网数据采集系统可靠性研究[J]. 制造业自动化, 2015, 37(4): 22-25. |
| [17] | 潘志新, 彭勇, 薛凤华. 110 kV及220 kV钢管铁塔输电线路带电作业安全距离试验研究[J]. 华东电力, 2012, 11(40): 2025-2028. |



