形状分析是计算机视觉、模式识别和计算机图形学中的基础性问题.形状的几何特征提取是形状分析的一个子方向, 常用的几何特征有凸度[1-2]、线性度[3-5]、紧密度[6]、椭圆度[7]和对称度[8]等.其中, 凸度在形状分解[9]、分类[10]和检索[11-12]等领域得到了广泛的研究, 在人类的视觉感知中扮演着重要角色[13-14].凸的物体具有显著的视觉特征和简单的几何特性[13, 15], 所以基于视觉显著性的模型分解往往把模型的凸度值作为分解的依据[9, 16-18], 这种基于凸度值的分解比单纯的基于严格凸模型的分解具有更好的鲁棒性, 而且可以把凸度值设为分解的阈值, 控制分解的细致程度[9].
在三维空间中, 只有当网格模型内任意两点之间的连线都在这个模型的内部时, 这个模型才是一个完全凸的模型.一般来说, 三维网格模型的凸度衡量方法需要满足以下4个基本条件[1, 19].
(1) 任意网格模型的凸度值都是一个实数, 并且在0到1之间.
(2) 只有当网格模型是完全凸的时候, 其凸度值才为1.
(3) 一定存在这样的网格模型, 它的凸度值无限接近于0.
(4) 凸度衡量方法对于给定的网格模型必须满足相似变换不变性.
1 相关工作本文将回顾几种常用的二维和三维凸度衡量方法.为了能区别二维和三维的凸度衡量方法, 我们用小写字母c表示二维凸度衡量方法, 用大写字母
二维凸度的衡量方法已经得到了广泛的研究, 其中最常用的是将形状本身的面积与其凸包的面积的比值作为凸度值[1].
定义1 给定一个二维形状
| $ \begin{align}c_1 (s)=\dfrac{{\rm Area}(s)}{{\rm Area}({\rm CH}(s))}.\end{align} $ | (1) |
公式(1)中,
| $ \begin{align}{\rm Per}({\rm CH}(s))\le {\rm Per}(s)\end{align} $ | (2) |
这样的关系, 当
定义2 给定一个二维形状
| $ \begin{align}c_2 (s)=\dfrac{{\rm Per}({\rm CH}(s))}{{\rm Per}(s)}.\end{align} $ | (3) |
因为c2是一种基于周长的凸度衡量方法, 它对边界的变化较为敏感, 所以抗噪性比c1要差.
还有一些与凸包无关的凸度衡量方法, 如Žunić等人[1]提出了一种基于边界投影的方法, 这种方法需要不断旋转图形来寻找一个使凸度值最小的外接矩形; Rosin等人[20]提出了一种具有对称性的凸度衡量方法, 与基于凸包的方法不同, 这种方法通过一个凸多边形去逼近原始多边形, 以这个凸多边形与原多边形的面积的比值作为凸度值; 在此方法的基础上, Kolensnikov等人[21]提出了一种基于动态规划的优化算法来计算最优拟合多边形; Rahtu等人[22]提出了一种基于概率的凸度衡量方法, 这种方法通过计算图形内任意两点连线上的某一点属于图形内部的概率来计算凸度.
1.2 三维网格的凸度衡量方法相比于二维凸度衡量方法, 三维网格的凸度衡量方法并没有得到广泛的研究.一些二维的凸度衡量方法可直接扩展到三维空间, 与定义1中的二维凸度衡量方法类似, 一种常用的基于体积的三维网格凸度衡量方法为网格自身体积与其凸包的体积之比.
定义3 给定一个三维网格
| $ \begin{align}C_1 (M)=\dfrac{{\rm Volume}(M)}{{\rm Volume}({\rm CH}(M))}.\end{align} $ | (4) |
值得注意的是, 本文所提及的三维网格都是三维封闭网格.与
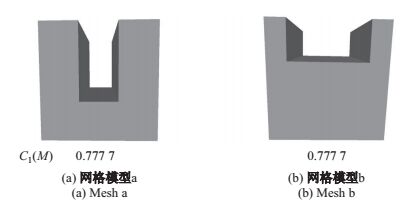
|
图 1 具有相同的体积与凸包体积的网格模型 Fig.1 Different meshes with identical mesh and convex hull volumes |
而一些二维的凸度衡量方法不能直接扩展到三维空间, 如果我们把基于边界的二维凸度衡量方法c2直接扩展到三维空间, 则二维空间中形状的边界可以看作是三维空间中网格的表面积.在二维空间中, 一定存在不等式(2), 但在三维空间中, 却不存在关于网格模型表面积与其凸包的表面积的不等式.这是因为对于一些类似于图 2的网格模型, 存在

|
图 2 一个具有很多空洞的立方体模型 Fig.2 A cube with many holes |
| $ \begin{align}{\rm Area}(M)>{\rm Area}({\rm CH}(M))\end{align} $ | (5) |
不等关系; 而对于一些类似于中空立方体的网络模型(见图 8), 却存在相反的不等关系
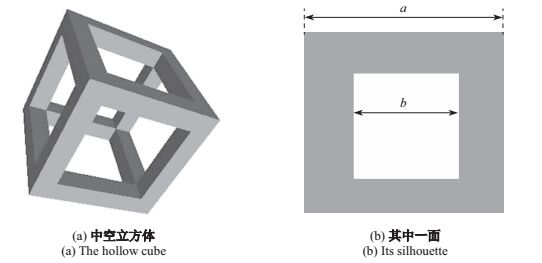
|
图 8 中空立方体 Fig.8 The hollow cube |
| $ \begin{align}{\rm Area}(M)<{\rm Area}({\rm CH}(M)).\end{align} $ | (6) |
因此, 不能直接将二维的c2扩展到三维空间.
为了解决方法C1对细长凹陷不敏感的问题, Lian等人[2]提出了一种基于投影的三维网格凸度衡量方法, 该方法是由文献[1]扩展而来.
定义4 给定一个三维网格模型
| $ \begin{align}C_2 (M)=\mathop {\min }\limits_{\alpha, \beta, \gamma \in [0, 2\pi]}\dfrac{P{\rm view}(M, \alpha, \beta, \gamma)}{P{\rm face}(M, \alpha, \beta, \gamma)}.\end{align} $ | (7) |
公式(7)中,
| $ \begin{align}P{\rm face}=P{\rm face}_x +P{\rm face}_y +P{\rm face}_z.\end{align} $ | (8) |
Pview是网格模型在平行于坐标平面的外包立方体上的投影面积之和, 因为外包立方体有6个面, 所以Pview可以表示为
| $ \begin{align}P{\rm view}=2(P{\rm view}_x +P{\rm view}_y +P{\rm view}_z).\end{align} $ | (9) |
图 3(a)表示网格模型中的一个三角面片在坐标平面上的投影.图 3(b)表示网格模型在三个坐标平面的投影, 即
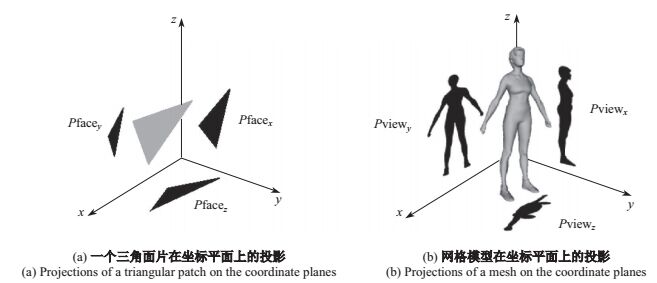
|
图 3 Pface与Pview的示意图 Fig.3 Pface andPview |
| $ \begin{equation}P{\rm face}\ge P{\rm view}, \end{equation} $ | (10) |
只有当网格模型为完全凸的时候等号才成立.而不断的旋转模型, 是为了找到一个最小的凸度值作为模型最终的凸度值.
由于最小化
基于以上问题, 本文提出了一种改进的三维网格模型的凸度衡量方法.该方法同样是一种基于投影的方法, 是对Lian的方法的一种改进.Lian的方法计算速度过慢的原因在于遗传算法需要多次计算投影面积, 而本文的思想是只在特定方向上投影一次, 再对在此方向上计算的投影比值进行修正, 以最后的修正值作为网格的凸度值.因为这种新方法结合了基于体积的方法和基于表面积的方法, 因此其具有基于体积的方法的抗噪性, 又能对细长的凹陷较为敏感, 而且相对于C2, 新方法大大缩短了计算时间.
2 改进的三维网格模型的凸度衡量本文提出了一种改进的三维模型凸度衡量方法, 通过旋转模型至某一固定方向, 并对3个坐标平面进行投影来估计凸度的初始值; 然后平行于每个坐标平面方向对模型进行切片, 通过计算切片的凸度值对初始估值进行修正, 从而得到最终的凸度值.该方法用公式表达为
| $ \begin{align}C_3 (M)={\rm Corr}\Big(\dfrac{P{\rm view}(MR)}{P{\rm face}(MR)}\Big), \end{align} $ | (11) |
其中, R是将网格旋转至特定方向的旋转矩阵, Corr( )是对初始估值的修正函数.
2.1 主方向上的初始估值如上所述, 我们希望通过旋转矩阵R把网格模型旋转至某一特定方向, 通过这一方式来替代Lian的方法中耗时的遗传算法.从定义4可知, 通过旋转模型至某一个特定方向,C2最终会达到一个最小值.一般来说, 只有当模型的所有面片在三个坐标平面投影具有最大重合时, C2才会达到最小值.因此, 我们的目标就是不通过优化算法, 只旋转一次就让投影重叠的面积接近于最大值.
这里我们采用了主成分分析(PCA)来对旋转方向进行估计, 这主要是基于以下两点原因.首先, PCA是一种常用的降维方法, 通过对数据集协方差矩阵进行特征分解, 得到数据集的主方向及其权值, 数据集在主方向上具有最大的方差.因此PCA可以保证面片在坐标平面上的投影具有相对较大的重叠面积, 从而获得一个相对较小的初始估值.其次, 在接下来的修正过程中, 垂直于主方向对模型进行切片比其他方向更能表示出模型的几何特征.
假设E为网格顶点的特征向量所组成的协方差矩阵, 把公式(11)中的参数R用E代替, 则在主方向上的凸度的初始估值
| $ \begin{align}C_e (M)=\dfrac{P{\rm view}(ME)}{P{\rm face}(ME)}.\end{align} $ | (12) |
图 4显示了4个三维网格模型的主方向, 以及模型在坐标平面上的投影.从图中可以看出, 初始估值
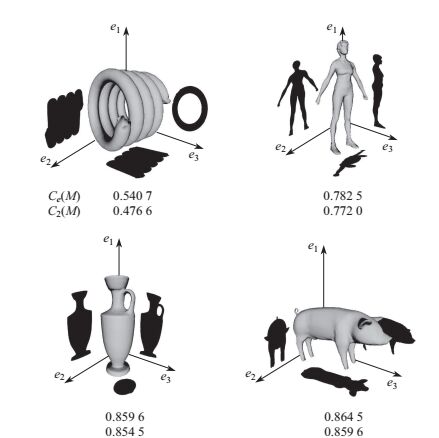
|
图 4 模型在主方向坐标系下的投影以及C2和Ce的值 Fig.4 Mesh silhouettes along the principal axes with the mesh convexity values calculated by C2 and Ce |
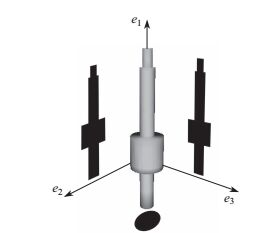
但在主方向上的估计也有一定的局限性.在Pview与Pface比值最小的方向上, 网格表面投影重叠最多, 而主方向只能反映网格顶点在此方向上的方差最大.对于不是完全凸的网格, 在主方向上可能没有投影重叠的表面, 即在主方向上比值为1.如图 5所示, 图中的网格是一个工程部件的模型, 可以计算出在主方向上的投影面积比为1, 但是它并不是完全凸的.通过以上的例子可以看出, 若直接用主方向上的比值代替最小比值作为网格的凸度值, 不能满足凸度衡量方法的条件2, 因此需要对主方向上的初始估值进行修正.
|
图 5 一个用PCA会产生错误估计的模型 Fig.5 An example whose convexity is overestimated by PCA |
缺少合理高效的三维网格凸度衡量方法的一个重要原因是三维模型比二维形状的复杂度高.若能将三维网格的凸度问题转化为二维形状的凸度问题, 那么借助于常用的二维凸度衡量方法, 三维网格的凸度也能方便的计算出来.在二维凸度计算中, c1和c2是最基本的凸度衡量方法, 我们把模型沿着主方向坐标轴进行切片, 通过对切片进行二维凸度值测量来对初始估值进行修正.
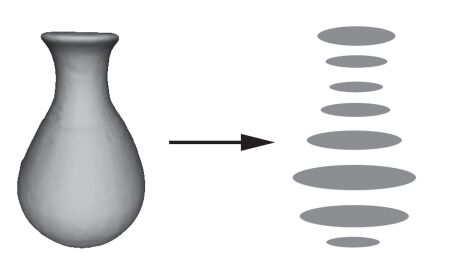
类似于医学上断层扫描的思想, 我们也可以在三个方向对网格模型进行``切片''.如图 6所示, 图中只显示了沿一个方向的切片, 此方向上的切片都是凸的, 但是在另外两个正交方向上存在凹切片.通过切片处理, 一个网格模型被转换为一系列的二维形状, 而这些二维形状的凸度则反映了原始网格的凸度值.因此, 我们使用这些二维形状的凸度值来计算每个主方向的修正系数.
|
图 6 三维网格切片示意图 Fig.6 An illustration of mesh slicing |
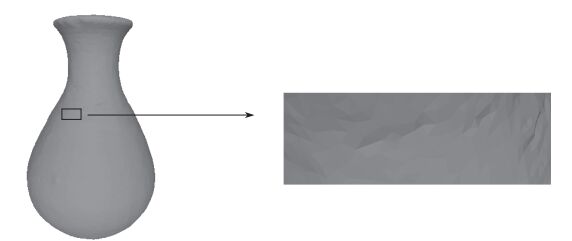
本文通过计算切平面与网格的交点得到切片, 由于网格模型的表面一般凹凸不平, 如图 7所示, 以上方法所得切片的边界常呈锯齿状, 而基于边界的方法c2对边界的变化非常敏感, 若采用c2进行凸度计算, 则会产生较大误差.因此我们采用基于面积的方法
|
图 7 三维网格表面 Fig.7 The surface of 3d mesh |
假设我们在某一方向上把三维网格模型切成N+1份, 每个切片之间是等距的, 则修正系数可以表示为
| $ \begin{align}r=\dfrac{\sum\limits_{i=0}^N {{\rm Area}(s_i)}}{\sum\limits_{i=0}^N {{\rm Area}} ({\rm CH}(s_i))}, \end{align} $ | (13) |
其中, Area(si)是第i个切片的面积,
| $ \begin{align}r=\dfrac{\sum\limits_{i=0}^N {\rm Area}(s_i)l_{\rm step}}{\sum\limits_{i=0}^N {\rm Area}({\rm CH}(s_i))l_{\rm step}}\approx \dfrac{{\rm Volume}(M)}{l_{\rm step} \sum\limits_{i=0}^N{{\rm Area}({\rm CH}(s_i))}}, \end{align} $ | (14) |
在N足够大的时候, 分子可约等于模型的体积.
为了使切片数量根据网格模型的精度自适应调整, 保留更多的几何特征, 我们提出平均网格边长的概念.网格模型中所有边长的平均值即为平均网格边长
| $ \begin{align}l_{\rm step} =\dfrac{1}{2}\overline{l}.\end{align} $ | (15) |
假设模型在某一主方向上最大的投影长度为
| $ \begin{align}N=\left\{\!\! {{\begin{array}{*{20}c} {N_{\max}, \quad L/l_{\rm step} \ge N_{\max} }, \\ {L/l_{\rm step}, \quad L/l_{\rm step} <N_{\max} }.\end{array} }} \right.\end{align} $ | (16) |
针对本文中用到的模型, 我们将
| $ \begin{align}r_j =\dfrac{{\rm Volume}(M)}{l_{\rm step} \sum\limits_{i=0}^{Nj}{{\rm Area}({\rm CH}(s_i))} }, \quad j=\{x, y, z\}.\end{align} $ | (17) |
定义5 对于一个给定的三维网格
| $ \begin{align}C_3 (M)=\dfrac{P{\rm view}(rME)}{P{\rm face}(ME)}, \end{align} $ | (18) |
其中,
| $ \begin{align}P{\rm view}(rME)=2(r_x P{\rm view}_x (ME)+r_y P{\rm view}_y (ME)+r_z P{\rm view}_z (ME)).\end{align} $ | (19) |
为了证明C3的可行性, 我们需要验证它是否满足凸度衡量方法的4个基本条件.
证 明:如果网格模型
为了证明条件3, 我们构造出一个中空的立方体, 如图 8所示.假设立方体的外边长为a, 内边长为b, 则
| $ \begin{align}r_x =r_y =r_z =\dfrac{a^2-b^2}{a^2}.\end{align} $ | (20) |
当不断增大b, 使其无限接近于a时,
| $ \begin{align}\mathop {\lim }\limits_{b\to a} C_3 (M)=0, \end{align} $ | (21) |
条件3得证.至此, 我们已经证明了定义C3满足凸度衡量的基本条件.
此外, 如果采用Lian的方法计算中空立方体的凸度, 则
| $ \begin{align}C_2 (M) & =\mathop {\min }\limits_{_{\alpha, \beta, \gamma \in [0, 2\pi]} } \dfrac{P{\rm view}(M, \alpha, \beta, \gamma)}{P{\rm face}(M, \alpha, \beta, \gamma)}\nonumber\\[1mm] & =\dfrac{12(a^2-b^2) }{12(a^2-b^2) +12({(a^2-b^2) -(a-b)^2})}\nonumber\\[1mm] & =\dfrac{a+b}{a+3b}.\end{align} $ | (22) |
如果不断减少b, 直到
| $ \begin{align}\mathop {\rm lim}\limits_{b\to a} C_2 (M)=\mathop {\lim}\limits_{b\to a} \dfrac{a+b}{a+3b}=\dfrac{1}{2}.\end{align} $ | (23) |
本文认为这是一种不合理的情况.
3 实验结果对比与分析本节我们对一些来自公共数据库里的模型进行定量分析.第3.1节与其他三维网格凸度衡量方法进行对比; 第3.2节与Lian的方法进行计算时间的对比.
3.1 实验分析为了证明本文方法的有效性, 我们采用McGill Articulated 3D Shape Benchmark和 Princeton Benchmark[23]数据库中的网格模型进行实验.在实验之前, 我们先对网格模型进行预处理, 将网格模型的重心设为坐标系原点.
图 9显示的是用不同凸度衡量方法计算出的凸度值, 网格模型按照C3的值进行排序.通过结果可以看出, 本文方法对模型1, 3, 6, 7和8计算的凸度值较低, 相反,C2的值较大.从模型18我们可以看出, 单纯基于体积的方法C1对于细长的凹陷并不敏感, 而C2和C3却能够给出合理的结果.由于公式(14)是一个近似计算, 对于球形模型会产生一个较大的误差, 所以模型23计算出的值并不是完全凸的.

|
图 9 不同凸度衡量方法的对比 Fig.9 The comparison of different convexity measures |
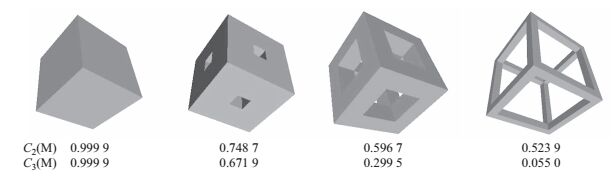
为了更好的表明C2与C3的区别, 我们人为设计了4个模型, 如图 10所示, 当内边界b分别等于0, 0.2a, 0.5a和0.8a时, C2与C3的凸度值不断地减少, 这符合我们的视觉感知.
|
图 10 不断增大b时的凸度值 Fig.10 The hollow cubes with broadeningb |
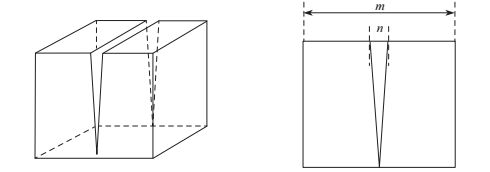
图 11显示的是一个具有较深凹槽的立方体, 当凹槽的宽度
|
图 11 一个具有深凹的立方体模型 Fig.11 A cube with a deep dent |
| $ \begin{array}{l} \mathop {{\rm{lim}}}\limits_{n \to 0} {C_1}(M) = \mathop {\lim }\limits_{n \to 0} \frac{{{\rm{Volume}}(M)}}{{{\rm{Volume}}({\rm{CH}}(M))}}\\ = \mathop {\lim }\limits_{n \to 0} \frac{{{m^3} - \frac{1}{2}{m^2}n}}{{{m^3}}} = 1. \end{array} $ | (24) |
然而这个值不能反映出凹槽的存在, 而C3却可以探测到这个凹槽的存在,
| $ \begin{align}\mathop {\rm lim}\limits_{_{n\to 0} } C_3(M)=\dfrac{6m^2}{8m^2}=0.75.\end{align} $ | (25) |
对于图 1的两个模型, C3计算出的凸度值分别为0.675~6和0.748~3, 即凹陷深的模型, 凸度值较低.而C1只受到凹陷的体积的影响, 没有考虑到凹陷是在模型的边缘区域还是内部区域.
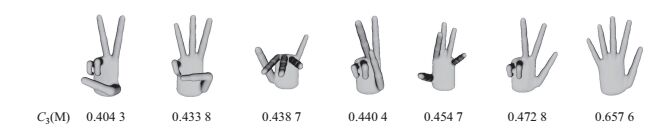
图 12显示的是同一手模型在不同姿势下的凸度.从图中可以看出, 5个手指完全张开时, 凸度值最大.而当手指弯曲的程度越高或弯曲手指越多时, 其凸度值越小, 这与人们心理上对凸度的衡量是一致的.
|
图 12 不同手势的凸度值 Fig.12 Hand gestures calculated by C3 |
本文从MPI-FAUST、McGill Articulated 3D Shape Benchmark和Princeton Benchmark 数据库中提取了80个网格模型, 共分为5个类别, 图 13显示的是其中的一些样本.我们把模型的凸度作为特征进行了分类实验, 实验采用的

|
图 13 5类模型的样本 Fig.13 Samples of 5 types of meshes |
Lian在算法中使用的参数为50个个体, 进行200次迭代.当网格模型的顶点非常多的时候, 此算法的执行速度较慢.与Lian的方法不同, 本文的方法避免使用遗传算法多次从帧缓存中读取图像, 而只需计算一次投影面积. 表 1显示了在计算网格模型的凸度时, 本文方法与Lian的方法在时间消耗上的对比.本文使用的实验环境是:CPU为Intel CORE i5;内存为6GB; 编程环境为Microsoft Visual Studio 2010. Lian的方法时耗的计算以从缓冲区读取图像的时间为基准, 再将此时间乘以迭代次数得到运行总时间(实际运行时间比表中显示的时间更长).从表中可以看出, 本文方法与Lian的方法相比, 大大减少了时耗.
| 表 1 时间消耗对比 Tab.1 Comparison of time consumptions |
为了解决现有三维网格模型凸度衡量方法的缺点, 本文提出了一种根据Lian的方法C2进行改进的方法C3.与C1相比, C3可以探测到细长的凹陷, 而且对于具有相同体积和相同凸包体积的模型, C3能够根据凹陷的深浅进行凸度计算, 而不是单纯的计算体积比, 这更加符合人类的视觉感知.与C2相比, C3通过引入基于面积的二维形状的凸度计算, 使该方法具有了基于体积的方法与基于投影的方法的特点.通过先确定主方向再进行投影, C3极大的缩短了C2的计算时间, 这使其更能适用于实际应用.
| [1] | ŽUNIĆ J, ROSIN P L. A new convexity measure for polygons[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(7): 923-934. DOI:10.1109/TPAMI.2004.19 |
| [2] | LIAN Z, GODIL A, ROSIN P L, et al. A new convexity measurement for 3D meshes[C]//Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on. IEEE, 2012:119-126. |
| [3] | ŽUNIĆ J, ROSIN P L. A rectilinearity measurement for polygons[C]//European Conference on Computer Vision. Berlin:Springer, 2002:746-758. |
| [4] | LIAN Z, ROSIN P L, SUN X. Rectilinearity of 3D meshes[J]. International Journal of Computer Vision, 2010, 89(2/3): 130-151. |
| [5] | ROSIN P L. A two-component rectilinearity measure[J]. Computer Vision and Image Understanding, 2008, 109(2): 176-185. DOI:10.1016/j.cviu.2007.09.010 |
| [6] | ŽUNIĆ J, HIROTA K, MARTINEZ-ORTIZ C. Compactness measure for 3D shapes[C]//Informatics, Electronics & Vision (ICIEV), 2012 International Conference on. IEEE, 2012:1180-1184. |
| [7] | ROSIN P L. Measuring shape:Ellipticity, rectangularity, and triangularity[J]. Machine Vision and Applications, 2003, 14(3): 172-184. DOI:10.1007/s00138-002-0118-6 |
| [8] | LEOU J J, TSAI W H. Automatic rotational symmetry determination for shape analysis[J]. Pattern Recognition, 1987, 20(6): 571-582. DOI:10.1016/0031-3203(87)90028-8 |
| [9] | REN Z, YUAN J, LIU W. Minimum near-convex shape decomposition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(10): 2546-2552. |
| [10] | ROSIN P L. Classification of pathological shapes using convexity measures[J]. Pattern Recognition Letters, 2009, 30(5): 570-578. DOI:10.1016/j.patrec.2008.12.001 |
| [11] | SARFRAZ M, RIDHA A. Content-based image retrieval using multiple shape descriptors[C]//Ieee/acs International Conference on Computer Systems and Applications. 2007:730-737. |
| [12] | YANG Y B, LIN H, ZHU Q. Content-based 3D model retrieval:A survey[J]. Chinese Journal of Computers, 2004, 27(10): 1297-1310. |
| [13] | BIEDERMAN I. Recognition-by-components:A theory of human image understanding[J]. Psychological Review, 1987, 94(2): 115 DOI:10.1037/0033-295X.94.2.115 |
| [14] | SIDDIQI K, KIMIA B B. Parts of visual form:Computational aspects[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(3): 239-251. DOI:10.1109/34.368189 |
| [15] | SINGH M, HOFFMAN D D. 13-part-based representations of visual shape and implications for visual cognition[J]. Advances in Psychology, 2001, 130: 401-459. DOI:10.1016/S0166-4115(01)80033-9 |
| [16] | LIU H, LIU W, LATECKI L J. Convex shape decomposition[C]//Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. IEEE, 2010:97-104. |
| [17] | GHOSH M, AMATO N M, LU Y, et al. Fast approximate convex decomposition using relative concavity[J]. Computer-Aided Design, 2013, 45(2): 494-504. DOI:10.1016/j.cad.2012.10.032 |
| [18] | ASAFI S, GOREN A, COHEN-OR D. Weak convex decomposition by lines-of-sight[J]. Computer Graphics Forum, 2013, 32(5): 23-31. DOI:10.1111/cgf.2013.32.issue-5 |
| [19] | 刘磊. 三维网格特征提取与分割[D]. 上海: 华东师范大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10269-1015351794.htm |
| [20] | ROSIN P L, MUMFORD C L. A symmetric convexity measure[J]. Computer Vision & Image Understanding, 2004, 103(2): 101-111. |
| [21] | KOLESNIKOV A, FRANTI P. Optimal algorithm for convexity measure calculation[C]//IEEE International Conference on Image Processing. 2005:353-356. |
| [22] | RAHTU E, SALO M, HEIKKILA J. A new convexity measure based on a probabilistic interpretation of images[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(9): 1501-1512. |
| [23] | CHEN X, GOLOVINSKIY A, FUNKHOUSER T. A benchmark for 3D mesh segmentation[J]. ACM Transactions on Graphics, 2009, 28(3): 341-352. |









