A joint construction research for multi-period medicine reverse logistics network with consideration of carbon emissions
0 引言
逆向物流网络节点包括回收点、预处理中心、再制造中心、垃圾处理点等[1].逆向物流网络模式有自建模式[2-3]、外包给第三方模式[4-5]、整合正向和反向模式[6-7]、多家企业共同建立以整合逆向物流资源的模式[8]即相关企业联建模式[9]等4种.对逆向物流网络进行规划不仅有助于优化资源, 还可以信息共享或通过规模经济降低总成本[10].
我国医药行业逆向物流发展比较缓慢, 过期药品或医疗器材的回收情况并不乐观.主要原因是各方的关注程度低[11], 如相关部门对过期药品或废旧医疗器材的回收重视程度不够、商家和民众的回收意识不强等, 从而导致有价值的物品得不到合理再利用.并且过期药品或废旧医疗器材随意丢弃还会造成环境污染.因此, 面对众多的过期药品和医疗器材, 采取可行的措施进行处理, 有利于经济发展的同时也能够达到保护环境的目的.
中国的经济发展大多以化石燃料为代价, 在创造经济增长的同时也造成了大量的碳排放, 因此怎样平衡我国的经济发展和碳排放以实现低碳经济成为了当前热点.此外, 中国科学院报告提出的发展低碳经济战略目标[12]是, 到2020年每单位国民生产总值要减少约50%的碳排放量.因此, 要求企业在发展经济的同时要减少碳排放量.过期药品和医疗器材的回收运作在很大程度上依赖于运输, 而在运输过程中往往造成大量的碳排放[13].此外, 供应链网络的运作是一个周期性的运作过程.
基于上述分析, 本文提出了考虑碳排放的多周期医药逆向物流网络联建模型, 并对医药企业逆向物流网络的构建和运作提出了建议.这里以回收过期药品或废弃医疗器材产品的系统总成本最小为目标函数, 并用算例验证该模型的有效性.
1 考虑碳排放的多周期医药逆向物流网络联建模型
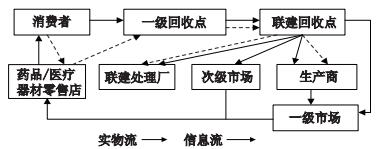
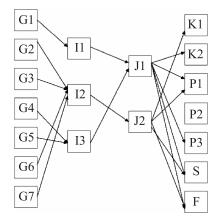
医药企业逆向物流联建网络结构图如图 1所示, 包含消费者、药品/医疗器材零售店、一级回收点、联建回收点、联建处理厂、生产商、一级市场、次级市场等8个元素.
1.1 模型基本假设
模型前提假设如下.
假设1, 退货\回收的药品或药品器材只能通过一级回收点运往联建回收点; 假设2, 联合企业的位置与数量已知, 并且每家药品/医疗器材零售店、一级回收点、联建回收点、联建处理厂、生产商的信息处理成本相同; 假设3, 运输成本与运输量、运输距离成简单的线性关系; 假设4, 备选的一级回收点、联建回收点、联建处理厂的处理能力有一定限制; 假设5, 生产厂商进行联盟, 对回收的产品具有相同的修复能力; 假设6, 运输单位成本已知; 假设7, 此网络系统只考虑联盟企业的逆向物流系统总成本, 并不涉及成本在企业间的分担.
1.2 模型中用到的符号 (下标)
$g \in \{1, 2, 3, \cdots, G\} $, 消费者; $i \in \{1, 2, 3, \cdots, I\}$, 一级回收点; $j \in \{1, 2, 3, \cdots, J\}$, 联建回收点; $k \in \{1, 2, 3,
\cdots, K\}$, 联建处理厂; $p \in \{1, 2, 3, \cdots, P\}$, 生产商; $f
\in \{1, 2, 3, \cdots, F\}$, 一级市场; $s \in \{1, 2, 3, \cdots, S\}$, 次级市场; $e \in \{1, 2, 3, \cdots, E\}$, 药品/器材销售店; $t \in
\{0, 1, 2, 3, \cdots, T\}$, 物流网络回收周期.
1.3 参数
$w_i^t, w_j^t, w_k^t $ : $分别为各节点建设的固定费用.
${mc}_i, {mc}_j, {mc}_k $ : $分别为各节点设施每使用一个周期的维护费用.
${ca}_i, {ca}_j, {ca}_k, {ca}_p, {ca}_f, {ca}_s $:分别为各节点产品的容量.
${pm}_{i}, {pm}_{j}, {pm}_{k}, {pm}_{p}, {pm}_{e} $:分别为各节点单位信息处理成本.
${uc}_i, {uc}_k, {uc}_{p}, {uc}_j^{ken}, {uc}_j^s $:分别为一级回收点、联建处理厂、生产商、联建回收点单位物品处理成本.
$\alpha, \beta, \gamma, \delta $:分别为联建回收点废弃率、二手率、原材料率和返还率.
$d_{gi}, d_{ij}, d_{jk}, d_{js}, d_{jp}, d_{jf} $:分别为两点之间的距离.
${tr}_{gi}, {tr}_{ij}, {tr}_{jk}, {tr}_{js}, {tr}_{jp}, {tr}_{jf}
$ : $分别为两点之间单位运输成本.
${pro}_{gi}^t, {pro}_{ij}^t, {pro}_{jk}^t, {pro}_{js}^t,
{pro}_{jp}^t, {pro}_{jf}^t $:分别为$t$周期内一点到另外一点的物品数量.
${mes}_i^t, {mes}_j^t, {mes}_k^t, {mes}_p^t, {mes}_e^t $:分别为$t$周期内, 一级回收点、联建回收点、联建处理厂、生产厂、药品或器材销售店信息处理量.
$t_{\rm carbon} $:碳排放税.
${pro}_{{\rm wei}}$:产品的平均重量.
$ c_{\rm carbon} $:每周期单位碳排放量.
1.4 决策变量
$x_i^t $ : $一级回收中心$i$是否在$t$周期建立, 为0和1变量.
${y}_{j}^t$:联建回收中心$j$是否在$t$周期建立, 为0和1变量.
$z_k^t $:联建处理厂$k$是否在$t$周期建立, 为0和1变量.
1.5 数学模型
|
$
{u}_{1} =\sum\limits_{i}^I {w}_{i}^{t}x_{i}^{t} +\sum\limits_i^I
{mc}_{i}{x}_{i}^{t} +\sum\limits_j^J {w}_{j}^{t} {y}_{j}^{t}
+\sum\limits_j^J {{{mc}}_{j} {y}_{j}^{t} } +\sum\limits_k^K
{w}_{k}^{t} {z}_{k}^{t} +\sum\limits_k^K{mc}_{k} {z}_{k}^{t};
$
|
(1) |
|
$
{u}_{2} =\sum\limits_{e}^{E} { {{mes}}_{e}^{t} {{pm}}_{e} }
+\sum\limits_{i}^{I} { {{mes}}_{i}^{t} {{pm}}_{i}}
+\sum\limits_{j}^{J} { {{mes}}_{j}^{t}{{pm}}_{j} }
+\sum\limits_{k}^{K} { {{mes}}_{k}^{t} {{pm}}_{k}}
+\sum\limits_{p}^{P} { {{mes}}_{p}^{t} {{pm}}_{p} };
$
|
(2) |
|
$
{u}_{3} =\sum\limits_{g}^{G}
{\sum\limits_{i}^{I} { {{pro}}_{{gi}}^{t} {{uc}}_{i} } }
+\sum\limits_{j}^{J} {\sum\limits_{k}^{K} { {{pro}}_{{jk}}^{t}
{{uc}}_{j}^{{ken}} } } +\sum\limits_{j}^{J} {\sum\limits_{p}^{P} {
{{pro}}_{{jp}}^{t} {{uc}}_{j}^{{ken}} } } +\sum\limits_{j}^{J}
{\sum\limits_{f}^{F} {{{pro}}_{{jf}}^{t}
{{uc}}_{j}^{{ken}} } }\\
~~~~~~~~~+\sum\limits_{j}^{J} {\sum\limits_{s}^{S} {
{{pro}}_{{js}}^{t} {{uc}}_{j}^{s} } } +\sum\limits_{j}^{J}
{\sum\limits_{k}^{K} { {{pro}}_{{jk}}^{t} {{uc}}_{k} } }
+\sum\limits_{j}^{J} {\sum\limits_{p}^{P} { {{pro}}_{{jP}}^{t}
{{uc}}_{P} } };
$
|
(3) |
|
$
{u}_{4} =\sum\limits_{g}^{G}
{\sum\limits_{i}^{I} { {{pro}}_{{gi}}^{t} {{tr}}_{{gi}} {d}_{{gi}} }
} +\sum\limits_{i}^{I} {\sum\limits_{j}^{J} { {{pro}}_{{ij}}^{t}
{{tr}}_{{ij}}{d}_{{ij}} } } +\sum\limits_{j}^{J}
{\sum\limits_{k}^{K} { {{pro}}_{{jk}}^{t} {{tr}}_{{jk}} {d}_{{jk}} }
}
\\
\, +\sum\limits_{j}^{J} {\sum\limits_{s}^{S} {
{{pro}}_{{js}}^{t} {{tr}}_{{js}}{d}_{{js}} } } +\sum\limits_{j}^{J}
{\sum\limits_{p}^{P} { {{pro}}_{{jp}}^{t} {{tr}}_{{jp}} {d}_{{jp}} }
} +\sum\limits_{j}^{J} {\sum\limits_{f}^{F} { {{pro}}_{{jf}}^{t}
{{tr}}_{{jf}}{d}_{{jf}} } };
$
|
(4) |
|
$
\begin{align}
u_5 &={pro}_{\rm wei}t_{\rm carbon} c_{\rm carbon} \left(
{\begin{array}{l}
\sum\limits_{g}^G {\sum\limits_i^I {{pro}_{gi}^t
d_{gi} } } +\sum\limits_i^I {\sum\limits_j^J {
{pro}_{ij}^t d_{ij} } } \\
+\sum\limits_j^J {\sum\limits_k^K {{pro}_{jk}^t
d_{jk} } } +\sum\limits_j^J {\sum\limits_s^S {
{pro}_{js}^t d_{js} } } \\
+\sum\limits_j^J {\sum\limits_p^P {{pro}_{jp}^t
d_{jp} } } +\sum\limits_j^J {\sum\limits_f^F {
{pro}_{jf}^t d_{jf} } } \\
\end{array}} \right);
\end{align}
$
|
(5) |
|
$
\begin{align}
\min U_{\sin } &=u_1 +u_2 +u_3 +u_4 +u_5;
\end{align}
$
|
(6) |
|
$
\begin{align}
\min U_{\rm mul} &=u_1 + u_2 +u_3 +u_4 + u_5.
\end{align}
$
|
(7) |
约束条件为
|
$
\sum\limits_g^G {\sum\limits_i^I {{pro}_{gi}^t } } =\sum\limits_i^I
{\sum\limits_j^J {{pro}_{ij}^t } };
$
|
(8) |
|
$
\sum\limits_i^I {\sum\limits_j^J {\mathop {pro}\nolimits_{ij}^t } }
=\sum\limits_j^J {\sum\limits_k^K {\mathop {pro}\nolimits_{jk}^t } }
+\sum\limits_j^J {\sum\limits_s^S {\mathop {pro}\nolimits_{js}^t } }
+\sum\limits_j^J {\sum\limits_p^P {\mathop {pro}\nolimits_{jP}^t } }
+\sum\limits_j^J {\sum\limits_f^F {\mathop {pro}\nolimits_{jf}^t }
};
$
|
(9) |
|
$
\sum\limits_{j}^J {\sum\limits_k^K {{pro}_{jk}^t } }
=\sum\limits_i^I {\sum\limits_j^J {{\alpha pro}_{ij}^t } }
\sum\limits_j^J {\sum\limits_s^S {{pro}_{js}^t } } =\sum\limits_i^I
{\sum\limits_j^J { {\beta pro}_{ij}^t } };
$
|
(10) |
|
$
\sum\limits_j^J {\sum\limits_p^P {{pro}_{jP}^t } }
=\sum\limits_i^I {\sum\limits_j^J {{\gamma pro}_{ij}^t } }
\sum\limits_j^J {\sum\limits_f^F {{pro}_{jf}^t } } =\sum\limits_i^I
{\sum\limits_j^J {\sum\limits_j^J {{\delta pro}_{ij}^t } } };
$
|
(11) |
|
$
\sum\limits_i^I {x_i^t } \ge 1, \sum\limits_j^J {y_j^t } \ge
1, \sum\limits_k^K {z_k^t } \ge 1;
$
|
(12) |
|
$
\sum\limits_g^G {\sum\limits_i^I {{pro}_{gi}^t } } \le
\sum\limits_i^I {{ca}_i }, \sum\limits_i^I {\sum\limits_j^J {
{pro}_{ij}^t } } \le \sum\limits_j^J {{ca}_i};
$
|
(13) |
|
$
\sum\limits_j^J {\sum\limits_{k}^K {{pro}_{jk}^t } } \le
\sum\limits_k^K {{ca}_k }, \sum\limits_j^J {\sum\limits_s^S {
{pro}_{js}^t } } \le \sum\limits_s^S {{ca}_s };
$
|
(14) |
|
$
\sum\limits_{j}^J {\sum\limits_p^P {{pro}_{jp}^t } } \le
\sum\limits_e^E {{ca}_e }\sum\limits_j^J {\sum\limits_f^F {
{pro}_{jf}^t } } \le \sum\limits_f^F {{ca}_f};
$
|
(15) |
|
$
\sum\limits_g^G {\sum\limits_i^I {{pro}_{gi}^t } }
=\sum\limits_i^I {{mes}_i^t } \sum\limits_i^I {\sum\limits_j^J {
{pro}_{i{j}}^t } } \sum{\sum{=\sum\limits_j^J { {mes}_j^t } } };
$
|
(16) |
|
$
\sum\limits_j^J {\sum\limits_k^K {{pro}_{jk}^t } }
=\sum\limits_k^K {{mes}_k^t }\sum\limits_j^J {\sum\limits_p^P {
{pro}_{jp}^t } } =\sum\limits_{jp}^P {{mes}_p^t };
$
|
(17) |
|
$
\sum\limits_g^G {\sum\limits_i^I {{pro}_{gi}^t } }
=\sum\limits_e^E {{mes}_e^t }.
$
|
(18) |
公式 (1) 表示单周期或多周期中, 一级回收点、联建回收点、联建处理厂的固定费用与维护费用之和.公式 (2) 表示药品或器材零售店、一级回收点、联建回收点、联建处理厂、生产商的信息处理成本.公式 (3) 表示初级回收点、联建回收点、联建处理厂、生产商的产品处理成本.公式 (4) 表示物流网络中的运输成本.公式 (5) 表示网络结构中碳排放的税费.公式 (6) 和公式 (7) 分别为单周期和多周期最小总成本.公式 (8) 到公式 (11) 各个物流节点之间的流量平衡.公式 (12) 表示至少有一个一级回收点、一个联建回收点、一个联建处理厂被选中.公式 (13) 到公式 (15) 表示确保运送到每个节点的产品数量不超过每个节点的容量.公式 (14) 到公式 (18) 表示信息量和产品数量相等.
2 算例
为方便计算, 本文假设单周期时间长度为1年; 每个季度药品和医疗器材使用情况有所波动, 因此本文选取每季度末期进行回收, 即多周期中1年有4个周期 (现实生活中周期长度以企业回收产品的实际时间为准, 这里以每个季度末尾作为回收时间).同样, 产品的回收数量也是如此, 模型中的数据如表 1、表 2所示[14-15].
表 1(Tab. 1

表 1 消费者区域坐标与一级回收中心之间最短距离
Tab.1 The shortest distance between the consumer area coordinates and the first recovery center
| 坐标/距离 |
X |
Y |
I1 |
I2 |
I3 |
| G1 |
0.48 |
0.59 |
10.20 |
7.40 |
5.50 |
| G2 |
0.43 |
0.55 |
10.50 |
13.80 |
11.20 |
| G3 |
0.42 |
0.58 |
18.80 |
6.00 |
5.00 |
| G4 |
0.50 |
0.63 |
15.70 |
0.94 |
2.30 |
| G5 |
0.52 |
0.62 |
13.20 |
4.70 |
2.30 |
| G6 |
0.38 |
0.48 |
18.20 |
5.30 |
7.00 |
| G7 |
0.22 |
0.40 |
10.80 |
5.30 |
5.20 |
| 注:数据来源于谷歌地图 |
|
表 1 消费者区域坐标与一级回收中心之间最短距离
Tab.1 The shortest distance between the consumer area coordinates and the first recovery center
|
表 2(Tab. 2

表 2 回收数量
Tab.2 The quantity of recovery goods
| 消费者区域 |
单周期回收数量 |
第一周期回收数量 |
第二周期回收数量 |
第三周期回收数量 |
第四周期回收数量 |
| G1 |
142 745 |
46 036 |
28 062 |
45 235 |
23 412 |
| G2 |
184 063 |
50 475 |
36 559 |
75 566 |
21 463 |
| G3 |
128 215 |
45 758 |
13 270 |
37 951 |
31 236 |
| G4 |
205 477 |
51 797 |
25 137 |
85 131 |
43 412 |
| G5 |
185 309 |
48 983 |
27 365 |
65 751 |
43 210 |
| G6 |
228 329 |
68 617 |
38 113 |
77 623 |
43 976 |
| G7 |
153 638 |
49 024 |
23 720 |
41 207 |
39 687 |
|
表 2 回收数量
Tab.2 The quantity of recovery goods
|
以上海地区为例, 在谷歌地图上随机选取7个区为拥有过期药品或医疗器材的消费者所在区域坐标位置, 分别为$G_{1}, G_{2}$, $\cdots, G_{7}$; 3个一级待选回收点区域坐标位置为$I_{1}, I_{2}, I_{3}$; 2个待选联建回收点区域坐标位置为$J_{1}, J_{2}$; 2个待选联建处理厂区域坐标位置分别为$K_{1}, K_{2}$; 待选次级市场和待选一级市场$S$, $F$以及3个生产商$P_{1}$,
$P_{2}$, $P_{3}$.以上数据如表 3、表 4所示.
表 3(Tab. 3

表 3 各网络节点之间最短距离
Tab.3 The shortest distance between network nodes
| d |
K1 |
K2 |
S |
F |
P1 |
P2 |
P3 |
I1 |
I2 |
I3 |
| J1 |
51.40 |
25.00 |
11.90 |
27.80 |
29.00 |
16.40 |
29.60 |
26.10 |
20.10 |
17.60 |
| J2 |
34.60 |
41.80 |
23.50 |
41.40 |
10.90 |
6.40 |
8.20 |
31.20 |
16.70 |
17.00 |
| 注:数据来源于谷歌地图 |
|
表 3 各网络节点之间最短距离
Tab.3 The shortest distance between network nodes
|
表 4(Tab. 4

表 4 模型中设定的变量值
Tab.4 The simulated value of parameters in the model
| 参数 |
符号 |
数值 |
| 废弃率 |
α |
10% |
| 二手率 |
β |
10% |
| 原料率 |
γ |
45% |
| 返还率 |
δ |
35% |
| 一级回收点i的最大回收产品数量 |
cai |
200 000 |
| 联建回收点j的最大处理产品数量 |
caj |
300 000 |
| 联建处理厂k的最大处理产品数量 |
cak |
300 000 |
| 生产商p的最大处理产品数量 |
cap |
200 000 |
| 次级市场s容纳的最大产品数量 |
cas |
300 000 |
| 一级市场f容纳的最大产品数量 |
caft |
1 050 000 |
| 一级回收点i在t周期固定投入费用 |
wit |
400 000 |
| 联建回收点j在t周期固定投入费用 |
wjt |
600 000 |
| 联建处理厂k在t周期固定投入费用 |
wkt |
500 000 |
| 一级回收点i设施维护费用 |
mci |
300 000 |
| 联建回收点心j设施维护费用 |
mcj |
450 000 |
| 联建处理厂k设施维护费用 |
mck |
350 000 |
| 信息处理单位成本 |
pm |
4 |
| 一级回收点产品单位处理成本 |
uci |
6 |
| 联建处理厂产品单位处理成本 |
uck |
4 |
| 生产商产品单位处理成本 |
ucp |
5 |
| 联建回收点产品单位处理成本 |
ucjken |
6 |
| 联建回收点产品单位处理成本 |
ucjs |
12 |
| 两点之间单位运输成本 |
tr |
1 |
| 碳排放税 |
trcarbon |
0.000 2 |
| 产品的平均重量 |
prowei |
1 |
| 每周期碳排放量 |
ccarbon |
25 |
|
表 4 模型中设定的变量值
Tab.4 The simulated value of parameters in the model
|
3 GA运算结果
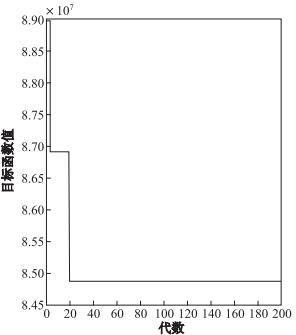
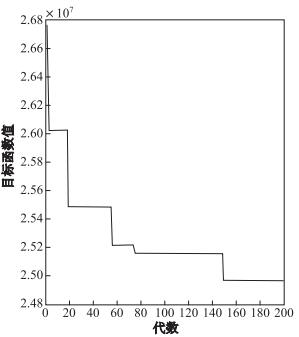
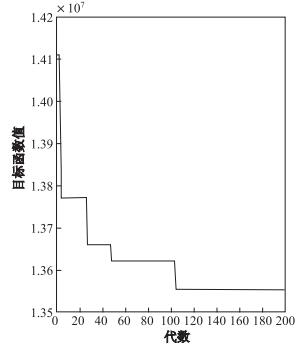
Michigan大学Holland教授于1975年提出遗传算法 (Genetic Algorithm, GA), 该算法是模拟自然进化过程, 搜索获得问题的近似最优值.由于此算法具有可靠性、通用性等优点, 因此逆向物流网络设计中, 常常采取此方法进行运算求最优值[16]. GA运算及结果如表 5及图 1至图 7所示.
表 5(Tab. 5

表 5 GA运算结果
Tab.5 Computational results
| 最优解 |
单周期 |
第一周期 |
第二周期 |
第三周期 |
第四周期 |
多周期 |
| 84 988 909 |
24 809 718 |
13 556 990 |
29 800 920 |
16 612 356 |
84 779 983 |
| Usin / Umul |
610 000 |
580 000 |
580 000 |
580 000 |
580 000 |
2 320 000 |
| u2 |
9 320 229 |
2 716 093 |
1 546 041 |
3 123 313 |
1 934 783 |
9 320 230 |
| u3 |
18 109 696 |
5 320 178 |
2 835 334 |
6 319 844 |
3 634 341 |
18 109 696 |
| u4 |
53 256 175 |
15 367 664 |
8 138 847 |
18 805 750 |
9 936 411 |
52 248 672 |
| u5 |
3 692 809 |
825 783 |
456 768 |
972 013 |
526 821 |
2 781 385 |
|
表 5 GA运算结果
Tab.5 Computational results
|
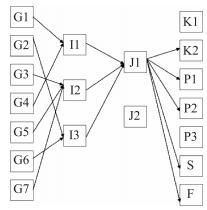
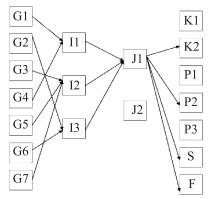
注:由于文章篇幅有限, 故选取单周期GA迭代图与多周期中第一、二周期迭代图作对比; 选取单周期节点配送图与多周期中第一、二周期节点配送图作对比.
(多周期中第三、四周期情况与单周期相比的情况与此类似)
由图所示, 多周期中的每一周期选择的节点 (图 6,
图 7) 比单周期选择的节点 (图 5) 要少.此外, 本文设计的网络具有以下3种优势.
第一, 本文中, 由于药品等回收数量的变化, 可以发现多周期各节点的位置在不同周期中是动态变化的, 因此这在日常生活中更符合实际情况.
第二, 多周期网络系统更经济.多周期网络中的总成本比单周期中的成本低0.25%.虽然单周期中固定成本和维护费用比多周期的要高, 但是多周期节点是动态的, 因此节点之间相对接近, 导致运输距离大幅减少.
第三, 碳税成本降低, 多周期的碳税成本降低了24.68%左右, 达到节能减排的目的; 医药 (医疗器具) 企业通过降低碳税成本 (减少碳排放量) 来遵守国家节能减排相关政策.
4 结语
本文构建了考虑碳排放下的多周期医药逆向物流网络联建模型, 并根据算例进行分析.结果表明, 此网络系统更符合现实生活、运作总成更经济、碳排放量明显减少, 从而验证了考虑碳排放下多周期医药逆向物流网络联建模型的有效性.该多周期逆向物流网络动态联建模型不仅适用于医药类逆向物流, 也适合于农产品收购、服饰类回收、废旧家电回收、塑料纸盒回收以及其它有质量问题产品的召回等情况.另外, 此网络结构也为构建地区性逆向物流网络、减少系统运作总成本、响应国家节能减排政策提供了借鉴.
但是在算例分析过程中, 本文只采取了一种方法 (GA) 进行计算分析, 因此可以考虑两种或更多的方法进行分析, 使得数据计算的结果更加精确 (可以采用其他的启发式算法来验证模型的可行性, 如粒子群算法 (Particle Swarm Optimization, PSO)、禁忌搜索 (Tabu Search, TS) 等); 同时, 在未来逆向物流网络联建的研究中, 不仅仅可以考虑碳排放这种情况, 还可以考虑整个废气的排放情况.