0 引言

众所周知, 网络知识可以被应用到经济学、数学、社会学等领域中, 而且图论在当今网络研究中的应用越来越多. 1736年, 瑞士数学家Euler发表了图论的第一篇论文, 解决了"哥尼斯堡七桥问题", 产生了著名的Euler图.中国的"一笔画"问题与Euler图和Euler迹关联.许多学者对Euler图的性质和应用进行了研究^[1-7].例如, Euler图在逻辑教学中有运用^[8].在网络信息安全研究中, 文献[9]给出了图形密码的研究.文献[10]给出了研究Euler图的综述.

一些学者还研究了超Euler图^[11-13].李登信等人的关于判定超Euler图的收缩法一文^[14]应用了Catlin的收缩法, 它是将图$G$的一个子图$H$收缩为一个点.这种收缩法虽然可以用来判定超Euler图, 但是它会使生成的新图中含有重边, 并丢失了原图的一些信息, 使得这种收缩法不具有恢复原图的"逆运算".李霄民在文献[15]中使用了撕裂法, 这种撕裂法与本文要介绍的顶点剖分运算、2-度顶点拆分运算不同, 但思想方法上有相似之处.

图论中的不少研究对象具有二种以上的等价命题, 如树、2-连通图、2-边连通图等^[16-18].本文从运算的角度出发, 力图表征Euler图的拓扑结构, 从多种角度来挖掘Euler图的本质, 得到了4个新的Euler图等价命题, 并利用图的"浓缩"和"稀释"运算给出刻画Euler图的方法, 且此方法能够转化为可行的算法.

1 定义

文中没有定义的术语和符号参见文献[1, 14].若途径$\omega=v_1e_1v_2e_2\cdots v_{k}e_kv_{k+1}$中的边$e_1$, $e_2$, $\cdots$, $ e_k$互不相同, 则称$\omega$为迹.经过图$G$的每条边的迹称为$G$的Euler迹(Euler trace). Euler环游(Euler tour)是闭Euler迹.一个图若包含Euler环游, 则称它为Euler图(eulerian graph).符号$N_G(u)$表示图$G$中与顶点$u$相邻的顶点之集, 叫做顶点$u$的邻集(adjacent set), 在不引起误会的情况下, 也可将符号$N_G(u)$简记为$N(u)$.图$G$的一组圈的集合$S=\{C_1, \cdots, C_m\}$若满足(1) $E(S)=E(G)$, 其中$E(S)=\bigcup^{m}_{i=1}E(C_i)$; (2)对于$1\leq i<j\leq m$, 有$E(C_i)\cap E(C_j)=\varnothing$, 则称$S$为图$G$的圈分解(cycle decomposition).类似地, 可定义图的迹分解(trace decomposition).

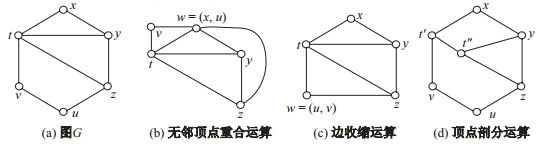
下面介绍本文要用到的3个图运算.在图$G$中, 对于任意2个不相邻的顶点$u$和$v$, 若$N(u) \cap N(v)=\varnothing$成立, 则可将$u$和$v$重合成一个顶点$w$, 也记为$w=(u, v)$, 并把这种运算叫做无邻顶点重合运算(non-adjacent identifying operation), 所得到的新图记为$G(u\circ v)$, 称$G(u\circ v)$为顶点叠加图(non-adjacent identifying graph).在图$G$中, 对于任意2个相邻的顶点$u$和$v$, 若有$N(u) \cap N(v)=\varnothing$, 则可移走边$uv$, 再对顶点$u$和$v$作无邻顶点重合运算, 把这种运算叫做边收缩运算(edge-contraction operation), 记对顶点$u$和$v$收缩边$uv$后的图为$G\circ uv$, 称$G\circ uv$为边收缩图(edge-contraction graph).对于图$G$中的顶点$u$, 若$d(u)=2m$, $m$是正整数, 它的邻集$N(u)=\{x_1, x_2, \cdots, x_{2m}\}$, 则可将$u$拆分成2个顶点$u'$, $u"$, 再用一条边连接$u'$和$u"$, 最后将$u'$和$u"$分别与$N(u)$中的顶点相连, 得新图$G'$, 称这种运算为顶点剖分运算(vertex-split operation).如果在$G'$中, $d_{G'}(u')$和$d_{G'}(u")$均为偶数, 则称这种运算为偶顶点剖分运算, 记对顶点$u$拆分后的图为$G*u$, 称$G*u$为偶点剖分图.

例1  图$G$的3种运算(见图 1):无邻顶点重合运算, 边收缩运算, 顶点剖分运算.

2 引理

如无特别说明, 下面提到的图$G$都是非平凡、有限、无向、简单、连通图.

引理2.1^[1]  若$\delta(G)\geq 2$, 则图$G$含有圈.

证明  当$|G|=3$时, 结论显然.对图$G$的一条边$uv$, 因$d_G(u)\geq \delta(G)\geq 2, d_G(v)\geq \delta(G)\geq 2$, 如$N(u) \cap N(v)\not=\varnothing$, 则说明$G$有一个三角形, 证毕.反之$N(u) \cap N(v)=\varnothing$, 可收缩边$uv$得图$G\circ uv$, 边$uv$收缩后的顶点为$w$, 其度数不小于2.根据数学归纳法, $G\circ uv$有一个圈$C$, 若$C$不含$w$, 则$C$就是$G$的一个圈.若$C$含$w$, 则将$w$拆分成$u$和$v$, 再用一条边将它们连接在一起, 恢复到$G$.相应地, 圈$C$也增大为图$G$的一个圈$C'$.证毕.

引理2.2^[1]  一个连通图是Euler图当且仅当它无奇度数顶点.

引理2.3^[1]  一个连通图有Euler迹当且仅当它最多有2个奇度数顶点.

证明  必要性.若$G$有开Euler迹, 由引理2.2, 这条开迹除起点和终点外的每个内部顶点都是偶度数顶点.

充分性.假设$G$是最多有2个奇度数顶点的非平凡连通图.若$G$无奇度数顶点, 则由引理2.2, $G$有闭Euler迹.否则, $G$恰有2个奇度数顶点$u$和$v$.此时, 设$G+uv$表示$G$中添加了一条连接$u$和$v$的新边$uv$所得到的图.显然, 图$G+uv$的每个顶点都是偶度数顶点, 由引理2.2, $G+uv$有Euler环游$C=v_0e_1v_1\dots e_{\varepsilon +1}v_{\varepsilon +1}$, 其中$e_1=uv$, 则$C-uv$是$G$的一条开Euler迹.

3 定理及其证明

定理3.1  设图$G$是非平凡、简单、连通图.则下面的命题两两相互等价.

(1) ^{[1, 10]}图$G$是Euler图.

(2) ^{[1, 10]}图$G$无奇度数顶点.

(3) ^[10]图$G$能分解为闭迹.

(4) ^[10]图$G$的每一个割集有偶数条边.

(5) ^[10]图$G$的每条边在$G$的奇数个圈上.

(6) ^[10]图$G$有奇数个圈分解.

(7) ^[10]$E(G)$中能包含在$G$的某个支撑树里的边子集(含空集)的个数为奇数.

(8) ^{[1, 10]}图$G$中存在$m$个边不交的圈$C_1, C_2, \cdots, C_m$, 使得$E(G)=E(C_1)\cup E(C_2)\cup\cdots \cup E(C_m)$.

(9) 去掉图$G$的任意一条边$e=uv$后, 所得之图$G-uv$有一条开Euler迹, 其中$G$不同构于完全图$K_4$.

(10) 设$u, v$是$G$中任意两个不相邻的偶度数顶点, 并满足$N(u) \cap N(v)=\varnothing$, 则对图$G$实施无邻顶点重合运算后的图$G(u\circ v)$是Euler图.

(11) 若边$uv\in E(G)$满足$N(u) \cap N(v)=\varnothing$, 则对图$G$实施边收缩运算后的图$G\circ uv$是Euler图.

(12) 如果顶点$u\in V(G)$的度数$d(u)=2m$, 则当$m\geq 2$时, 对图$G$实施偶顶点剖分运算后的图$G*u$是Euler图.

证明  在文献[10]中已有"$(i) \Rightarrow (i+1)$"$(i=1, 2, \cdots, 7)$的证明, 以下证明从命题(8)开始. "$(i)\Rightarrow (k) $"表示由命题$(i)$来推证命题$(k)$, 其中$i$依次取8, 9, 10, 11, 12, 且$k$依次取9, 10, 11, 12, 1.

(8) $\Rightarrow$(9)因为边集合$E(G)={\bigcup_{i=1}^m}E(C_i)$, 易得到图$G$有一条Euler环游.去掉某个圈$C_i$上的边$uv$, 那么顶点$u$和$v$就变成了2个奇度数顶点, 由引理2.3, 知道图$G$有一条起点为$u$、终点为$v$的开Euler迹.

(9) $\Rightarrow$(10)取$G$中任意两个不相邻的偶度数顶点$u, v\in V(G)$, 且有$N(u) \cap N(v)=\varnothing$, 得图$H=G+uv$.根据命题(9), 图$H-uv$有一条以$u$为起点、$v$为终点的开Euler迹$T$.对图$G$的不相邻顶点$u$和$v$实施无邻顶点重合运算后, 图$H-uv$的开Euler迹$T$的起点和终点重合, 得图$G(u\circ v)$的Euler环游$T(u\circ v)$, 证得命题(10).

(10) $\Rightarrow$(11)取满足$N(u) \cap N(v)=\varnothing$的边$uv\in E(G)$.令$H=G-uv$, 则由命题(10), 知$H(u\circ v)$有一条Euler环游$C$.注意到图$H(u\circ v)=G\circ uv$, 从而命题(11)得证.

(11) $\Rightarrow$(12)拆分$G$的偶度数顶点$w$为2个顶点$w_1$和$w_2$, 再用一条边连接顶点$w_1$和$w_2$, 对偶度数顶点$w$做偶顶点剖分运算, 得$H=G*w$.根据边收缩图的定义以及命题(11), $H\circ w_1w_2$有一条Euler环游$C$.恰好图$G=H\circ w_1w_2$, 也就是说, 环游$C$也是图$G$的Euler环游, 能够看到图$C*w$是$H$的Euler环游, 则命题(12)得证.

(12) $\Rightarrow$(1)对$d(w)=2m$ ($m\geq 2$)的顶点$w\in V(G)$, 由命题(12)得图$H=G*w$有Euler环游$C$, 则图$G=H\circ w_1w_2$有Euler环游$C\circ w_1w_2$, 命题(1)得证.

以上过程证明了命题$(i)$成立的充要条件是命题$(k)$成立.本定理得证.

下面对Euler图进行"浓缩"和"稀释".如果图$H$的任何一对不相邻顶点$u$和$v$的邻点集合$N_H(u)$和$N_H(v)$满足$N_H(u) \cap N_H(v)\not=\varnothing$, 则称图$H$为顶点叠加图(vertex-overlapping graph).显然, 顶点叠加图$H$是连通图.

对顶点叠加图$H$的任何一对不相邻顶点$u$和$v$, 定义$J(u, v)=N_H(u) \cap N_H(v)$, 则有$H$的顶点子集$X=\bigcup _{uv\not \in E(H)}J(u, v)$的顶点导出子图$H[X]$, 对于任意不属于$X$的顶点$w$都与顶点导出子图$H[X]$有边相连.显然, 顶点叠加图$H$的顶点导出子图$H[X]$是连通的.反设子图$H[X]$是不连通的, 则$H[X]$至少有2个分支$H_i$和$H_j$.任取顶点$x_i\in V(H_i)$和$x_j\in V(H_j)$, 按照顶点叠加图$H$的定义$N_H(x_i) \cap N_H(x_j)\not=\varnothing$, 即分支$H_i$和$H_j$是连通的, 矛盾.称$H[X]$为顶点叠加图$H$的中心(center).顶点叠加图$H$的中心$H[X]$的最小连通子图$H_{ker}$是使得$V(H_{ker})\cap J(u, v)\not=\varnothing$对顶点叠加图$H$的任何一对不相邻顶点$u$和$v$成立, 称$H_{ker}$为顶点叠加图$H$的中心核图(centrally kernel graph).以下规定:若顶点叠加图$G_k$是完全图, 则它有一棵$n$个顶点的星作为它的中心核图.

连通图$G$的$2$-度顶点拆分运算($2$-degree split operation)定义为:把图$G$的每个度数$d_G(u)\geq 4$的顶点$u$剖分开为2个顶点$u', u"$, 并将顶点$u', u"$与顶点$u$的邻点分别相连, 得到的新图记为$G \wedge u$, 且有$d_{G \wedge u}(u")\geq d_{G \wedge u}(u')=2$, 以及$d_{G \wedge u}(u")+ d_{G \wedge u}(u')=d_G(u)$.如果$G \wedge u$是2-边连通, 则说对$u$实施了一次$2$-边连通$2$-度顶点拆分运算($2$-edge-connected $2$-degree split operation).如何保证在$2$-度顶点拆分运算后的图是2-边连通的呢？可以按照如下办法进行剖分:设$G$连通, 对于任意顶点$u\in V(G)$, 有$N(u)=\{x_1, x_2, \cdots, x_m\}$.对$u$执行一次$2$-度顶点拆分运算后, $2=d_{G \wedge u}(u')\leq d_{G \wedge u}(u")$, 但$G \wedge u$不连通.设$N_{G \wedge u}(u')=\{x_i, x_j\}$, 则可重新剖分$u$为$t', t"$, 使得$t"$与$N(u)$中$x_i$和$x_s(s\neq j)$相连, $t'$与剩余的顶点相连, 得到一个$2$-边连通图$G \wedge u$.注意到, 如果图$G$本身是1-边连通的, 采用上面的方法得到的新图$G \wedge u$依然是1-边连通的.一般地, 顶点拆分运算和无邻顶点重合运算互为逆运算.须指出, 文献[10]中有边分裂方法, 但是边分裂方法与本文对顶点的$2$-边连通$2$-度顶点拆分运算完全不同, 关键是文献[10]的边分裂方法没有指明$2$-边连通性, 操作的时候可能造成不连通性.

定理3.2  图$G$是Euler图的充要条件为对$G$的任意不相邻的偶度数顶点做一系列无邻顶点重合运算后, 可得图$G$的顶点叠加图$G^*$, 使得$G^*$的中心核图是一棵树.

证明  必要性.设图$G$是Euler图, 记$G=G_1$.若图$G_{1}$有一对不相邻的顶点$u_1$和$v_1$, 使得它们邻集的交$N_{G_1}(u_1) \cap N_{G_1}(v_1)=\varnothing$, 那么对$G_1$的顶点对$u_1$和$v_1$做一次无邻顶点重合运算, 得到图$G_2=G_1(u_1\circ v_1)$.由定理3.1, 知$G_2$是Euler图.若图$G_2$有一对不相邻的顶点$u_2$和$v_2$, 使得这2个顶点的邻集的交$N_{G_2}(u_2) \cap N_{G_2}(v_2)=\varnothing$, 可对$G_2$的顶点对$u_2$和$v_2$再做一次无邻顶点重合运算, 得到图$G_3=G_2(u_1\circ v_1)$, 定理3.1说$G_3$也是Euler图.如此进行下去, 直到$G_{k}$是Euler图, 但对Euler图$G_k$的任意一对顶点$u_k$和$v_k$, 它们的邻集的交$N_{G_k}(u_k) \cap N_{G_k}(v_k)\neq \varnothing$, 也就是说, 图$G_k$是顶点叠加图, 且每个顶点的度数均为偶数.令$n=|V(G_k)|$是顶点叠加图$G_k$的顶点数目.

根据规定, 若顶点叠加图$G_k$是完全图, 则它有一棵$n$个顶点的星作为它的中心核图.如果图$G_k$不是完全图, 取$G_k$的顶点子集$X=\bigcup _{uv\not \in E({G_k})}J(u, v)$, 其中$J(u, v)=N_{G_k}(u) \cap N_{G_k}(v)$, 得到$G_k$的顶点导出子图$G_k[X]$, 简记为$H_1=G_k[X]$.由于$G_k$是顶点叠加图, 所以它是连通的, 则顶点子集$X$导出的图$H_1$也是连通的.顶点导出图$H_1$的顶点集可表示成2个不交子集的并$V(H_1)=S_1\cup T_1$, 使得每一个顶点$x_i\in S_1=\{x_i\mid i=1, 2, \dots, m\}, $对顶点叠加图$G_k$的任意一对不相邻的顶点$u, v$, 满足$V(H_i-x_i)\cap J(u, v)\not = \varnothing$, 其中$H_{i+1}=H_i-x_i$($i=1, 2, \cdots, m$), 这里$m$是最大的, 也就是说, 图$H_{m+1}=H_m-x_m$中没有顶点$w$, 使对顶点叠加图$G_k$的任意一对不相邻的顶点$u, v$, 满足$V(H_{m+1}-w)\cap J(u, v)\not = \varnothing$.如果图$H_{m+1}$不连通, 则有2个顶点$z, z'\in V(H_{m+1})$, 在图$H_{m+1}$中没有路连接, 也就是顶点$z, z'$在顶点叠加图$G_k$中不相邻.根据图$H_{m+1}$的定义, $V(H_{m+1})\cap J(z, z')\not = \varnothing$, 这与顶点$z, z'$在图$H_{m+1}$中没有路连接矛盾, 即假设不真.则连通图$H_{m+1}$至少含一棵支撑树, 它也是顶点叠加图$G_k$的中心核图.

充分性.记满足定理要求的图$G=G_1$, 对图$G_1$的一对满足$N_{G_1}(u_1) \cap N_{G_1}(v_1)=\varnothing$的不相邻顶点对$u_1$和$v_1$做一次无邻顶点重合运算, 得图$G_2=G_1(u_1\circ v_1)$.相同地, 有$i=2, 3, \cdots, L$, 可得图$G_i=G_{i-1}(u_{i-1}\circ v_{i-1})$, $u_{i-1}v_{i-1}\not\in E(G_{i-1})$, 且$N_{G_{i-1}}(u_{i-1}) \cap N_{G_{i-1}}(v_{i-1})=\varnothing$, 使得图$G_L$的任意一对顶点$u$和$v$的邻集的交$N_{G_L}(u) \cap N_{G_L}(v)\neq \varnothing$, 即图$G_L$是顶点叠加图.上面已经证明顶点叠加图$G_L$的中心核图是一棵树.由定理3.1, 顶点叠加图$G_L$是Euler图, 设$C_L$是它的Euler环游.因为$G_L=G_{L-1}(u_{L-1}\circ v_{L-1})$, 设Euler环游$C_L$上的顶点$w_L$是图$G_{L-1}$的不相邻顶点对$u_{L-1}$和$v_{L-1}$重合后的顶点, 对图$G_L$的顶点$w_L$实施$2$-边连通$2$-度顶点拆分运算后, 并恢复它们在图$G_{L-1}$中的连接方式, 得图$G_{L-1}=G_L \wedge w_L$, 且$C_L \wedge w_L$是图$G_{L-1}$的Euler环游.一般地, 对$k=2, 3, \dots, L$, 图$G_{k}$的Euler环游$C_k$上的顶点$w_k$是图$G_{k-1}$的不相邻顶点$u_{k-1}$和顶点$v_{k-1}$重合后的顶点, 对图$G_k$的顶点$w_k$实施$2$-边连通$2$-度顶点拆分运算后, 得到顶点$u_{k-1}$和顶点$v_{k-1}$, 并恢复它们在图$G_{k-1}$中的连接方式, 得到图$G_{k-1}=G_k \wedge w_k$, 且$C_k \wedge w_k$是图$G_{k-1}$的Euler环游, 这就证明了$G$是Euler图.

由上述定理得到：任何一个Euler图是将某个圈$C_n$进行一系列无邻顶点重合运算而来的.

定理3.3  图$G$是Euler图的充要条件为对$G$进行一系列$2$-边连通$2$-度顶点拆分运算到图$H$, 使得当2-边连通图$H$不存在可进行$2$-度顶点拆分运算的顶点时, 图$H$一定是Hamilton圈$C_{|E(G)|}$.

证明  必要性.对Euler图$G$每执行一次$2$-边连通$2$-度顶点拆分运算, 都会有一个顶点是2度, 使得$d(u')\geq d(u")=2$, 其中$u'$, $u"$是$ u$拆分成的2个顶点, 且得到的$G_i$都是2-边连通的.因此, 当$\Delta(G_i)>2$时, 就执行一次$2$-边连通$2$-度顶点拆分运算, 当$\Delta(G_i)=2$时, 所有顶点的度都是2, 得到的$G_\Delta$一定是一个圈.下面计算$C_n$中$n$的大小.由$2$-度顶点拆分运算的定义得, 执行$2$-度顶点拆分运算, 不改变原图$G$的边数, 因此, $n=|E(G)|$.

充分性.对图$G$每执行一次$2$-边连通$2$-度顶点拆分运算, 都得到的$G_i$都是2-边连通.当$\Delta(G_i)>2$时, 就执行一次$2$-边连通$2$-度顶点拆分运算, 直到2-边连通图$G_n$不存在可进行$2$-度顶点拆分运算的顶点.已知图$G_n$一定是Hamilton圈$C_{|E(G)|}$, 显然, $C_{|E(G)|}$是2-边连通的, 那么图$G$不可能是1-边连通的, 否则与$C_{|E(G)|}$是2-边连通的矛盾.由于$G_n$的所有顶点的度都是2, 由定理3.1, 知$G_n$是Euler图.已知$2$-边连通$2$-度顶点拆分运算和无邻顶点重合运算互为逆运算.那么, 按照图$G$执行$2$-边连通$2$-度顶点拆分运算的顺序, 倒着对圈$C_{|E(G)|}$使用无邻顶点重合运算, 就可以得到图$G$.由定理3.1, 证得$G$是Euler图.充分性得证.

文献[10]的推论5.10用边分裂方法给出:一个图$G$有Euler迹$T$当且仅当通过对次大于2的顶点反复使用边分裂方法能把$G$变换为一个圈.但是因为定理3.3中使用的对顶点的$2$-边连通$2$-度顶点拆分运算与推论5.10中使用的边分裂方法不同, 所以本文的定理3.3也是一种等价证明.

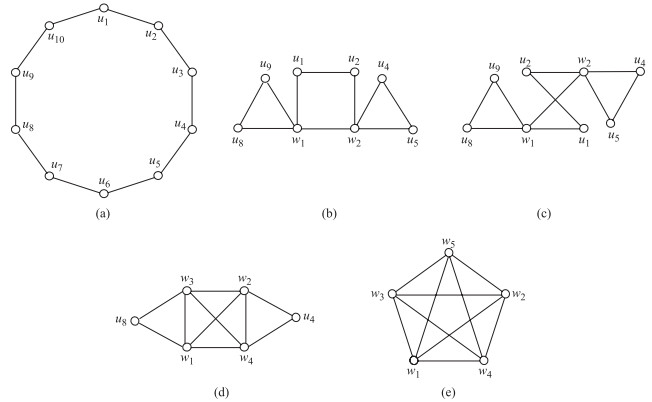
例2  $K_5$是Euler图, 它是对圈$C_{10}$实施一系列无邻顶点重合运算得来的.在图 2中, 将顶点$u_7, u_{10}$重合得顶点$w_1$, 记为$w_1=(u_7, u_{10})$, 其余的是$w_2=(u_3, u_{6})$, $w_3=(u_2, u_{9})$, $w_4=(u_1, u_{5})$, $w_5=(u_4, u_{8})$; 过程$(a)\rightarrow (b)\rightarrow (c)\rightarrow (d)\rightarrow (e)$是对$C_{10}$进行无邻顶点重合运算后得到$K_5$.反过来, 过程$(e)\rightarrow (d)\rightarrow (c)\rightarrow (b)\rightarrow (a)$是对$K_5$实施$2$-边连通$2$-度顶点拆分运算后得到的.

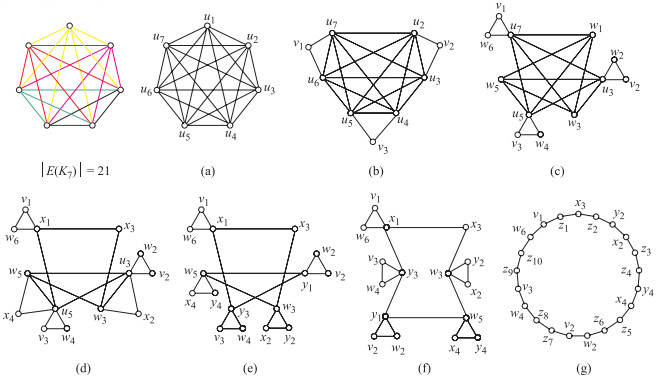
例3  圈$C_{21}$ 是对 $K_7$ 实施一系列 $2$-边连通 $2$-度顶点拆分运算得来的.在图 3中, 过程 $(a)\rightarrow (b)$ 是将顶点 $u_1$ 拆分得顶点 $v_1, v_2, v_3$; 过程 $(b)\rightarrow (c)$是将顶点$u_2$拆分得顶点$w_1, w_2$, 顶点$u_4$拆分得顶点$w_3, w_4$, 顶点$u_6$拆分得顶点$w_5, w_6$; 过程$(c)\rightarrow (d)$是将顶点$u_7$拆分得顶点$x_1, x_2$, 顶点$w_1$拆分得顶点$x_3, x_4$; 过程$(d)\rightarrow (e)$是将顶点$u_3$拆分得顶点$y_1, y_2$, 顶点$u_5$拆分得顶点$y_3, y_4$; 过程$(e)\rightarrow (f)$是为了使平面图$ (e)$更加一目了然; 过程$(f)\rightarrow (g)$是将顶点$x_1$拆分得顶点$z_1, z_{10}$, 顶点$w_3$拆分得顶点$z_2, z_3$, 顶点$w_5$拆分得顶点$z_4, z_5$, 顶点$y_1$拆分得顶点$z_6, z_7$, 顶点$y_3$拆分得顶点$z_8, z_9$.过程$(a)\rightarrow (b)\rightarrow (c)\rightarrow (d)\rightarrow (e)\rightarrow (f)\rightarrow (g)$是对$K_7$进行$2$-边连通$2$-度顶点拆分运算后得到$C_{21}$.反过来, 过程$(g)\rightarrow (f)\rightarrow (e)\rightarrow (d)\rightarrow (c)\rightarrow (b)\rightarrow (a)$是对$C_{21}$实施无邻顶点重合运算后得到的.

由上述例子可以断言:对正整数$q=\frac{1}{2}n(n-1)$ (奇数$n\geq 3$), 总可以恰当地对圈$C_q$实施一系列无邻顶点重合运算后得到一个完全图$K_n$.反之, 对完全图$K_n$ (奇数$n\geq 3$)恰当地实施一系列$2$-边连通$2$-度顶点拆分运算后得到一个圈$C_q$.设图$G$是Euler图, 由此得到新概念:浓缩度是用来描述一个圈$C_q$或有$p$个顶点、$q$条边的$(p, q)$-图$G$"浓缩"成一个完全图$K_n$ (奇数$n\geq 3$)的步骤复杂程度的量, 也就是说, 记录对一个圈$C_q$或$(p, q)$-图$G$实施无邻顶点重合运算次数den$(G)$.另一个新概念:稀释度, 记为spa$(G)$, 是度量将一个图"稀释"成圈的程度.注意到, 对$(p, q)$-图$G$的一个偶度数$d_G(u)\geq 4$的顶点实施一系列$2$-边连通$2$-度顶点拆分运算的次数为$\frac{1}{2}d_G(u)-1$, 那么, 稀释$(p, q)$-图$G$到圈$C_q$则需要进行$\sum_{u\in V(G)}[\frac{1}{2}d_G(u)-1]=q-p$次$2$-边连通$2$-度顶点拆分运算, 即稀释度spa$(G)=q-p$.例如, 将完全图$K_n$ (奇数$n\geq 3$) "稀释"成圈$C_q$的稀释度为spa$(K_n)=q-n$.反过来, 将圈$C_q$ "浓缩"成完全图$K_n$的浓缩度为den$(C_q)=q-n$.

4 总结与问题

本文通过几个图运算, 将Euler图的拓扑性质简单直观地给出, 便于理解Euler图的性质.本文的4种运算可以看做网络运算, 其中边收缩运算和顶点剖分运算互为逆运算, 无邻顶点重合运算和$2$-边连通$2$-度顶点拆分运算互为逆运算.注意到, 逆运算不可缺少$N(u) \cap N(v)=\varnothing$的条件, 否则会造成度数的缺失以及重边和自环的产生.本文利用运算给出非Euler图的一个刻画.对连通图$G$的满足$N_{G}(u) \cap N_{G}(v)=\varnothing$的一对不相邻的顶点$u$和$v$实施无邻顶点重合运算, 重合后的顶点$w$可以分为2类:如果$d(u)$和$d(u)$均为奇数, 称$w$为伪偶顶点, 其余为正常顶点.那么, 可以对一个非Euler图进行一系列无邻顶点重合运算, 按照定理3.2, 最后得到顶点叠加图必含有奇数度顶点或伪偶顶点.

本文定理3.1中的12个等价命题分别从不同的角度刻画了Euler图.命题(1)是对Euler图的最经典的定义, 为大多数教科书所使用, 虽然这种定义很自然, 但是仍需要其他简洁、直观的刻画, 这也是本文探究Euler图的等价命题的目的所在.命题(2)从顶点度的角度出发, 较为直观地描述了Euler图.命题(3)从Euler图的拓扑结构的角度出发, 简洁地刻画了Euler图.从命题(9)到命题(12)则都是含有各种加、减边以及加、减顶点的运算, 从而为2个拓扑结构不同的Euler图之间建立了桥梁, 也为从已知Euler图生成新的Euler图提供了有效、可行的方法, 其中运用了数学的图形转换.此外, 本文得到了一个新结论(定理3.2).对一个图$G$进行一系列无邻顶点重合运算, 直至得到图$G$的顶点叠加图, 这种方式是将图$G$ "浓缩".相反, 利用$2$-边连通$2$-度顶点拆分运算, 可将图$G$ "稀释".对若干个简单情形进行"运算"来"合成"复杂情形, 又可以将复杂情形"分解"为数个简单情形, 最终建立它们之间的等价关联.由于"一个图是Euler图的充要条件是它的线图为Hamilton图"较为直观, 故没有直接写成定理的形式.

需要指出的是:定理3.1中命题(9)到命题(12)是本文新提出的, 因此给出较为详细的证明.受引理2.3的启发, 本文从加、减边的运算角度出发得到命题(9);命题(10)中提到在满足$N(u) \cap N(v)=\varnothing$的条件下实施无邻顶点重合运算, 可避免重边和自环的情形出现, 虽然文献[14]提到边分裂方法有逆运算, 但没有给出确切的定义; 命题(11)中提到在满足$N(u) \cap N(v)=\varnothing$的条件下实施边收缩运算, 可避免重边和环的情况出现, 这与文献[10]中收缩图的某条边不同; 命题(12)中提到的偶顶点剖分运算是新的运算, 在文献[10]中没有发现类似的方法.

还有一些值得研究且有意义的问题, 譬如:有向Euler图的等价命题, Hamilton圈$C_n$可以"浓缩"成Euler图的种类和个数, 以及"浓缩"的方法等, 这些都是将要深入研究的问题.