互联网的迅速发展使得网络信息资源越来越丰富, 但在满足用户对信息需求的同时也引发了信息过载问题, 用户往往需要花费大量时间和精力从海量数据信息中筛选出对自己有用的信息.搜索引擎虽然能在一定程度上解决这种问题, 但无法满足用户个性化的需求, 因此个性化推荐系统应运而生.个性化推荐系统是建立在海量数据挖掘基础之上的一种智能平台, 它根据用户个人信息, 比如用户的兴趣特点和购买行为等, 向用户推荐其可能感兴趣的其他信息, 从而为用户提供个性化的信息服务和决策支持, 比如淘宝的购物推荐、Amazon的购书推荐、豆瓣的电影推荐等均是典型的个性化推荐系统应用案例.推荐系统根据推荐算法的不同可分为基于内容的推荐、协同过滤推荐、混合推荐等3类.协同过滤推荐在如今个性化推荐系统中有着广泛的应用, 算法主要可以分为基于记忆[1-3]和基于模型[4-6]这两类.基于记忆的协同过滤是根据用户或者项目之间的相似性来进行预测推荐.基于模型的协同过滤与基于记忆的协同过滤不同点在于, 基于模型的算法是对已有数据, 即收集到的用户历史数据信息, 如商品评分、网页浏览记录等, 运用统计学以及机器学习方法进行分析学习, 挖掘用户的偏好和行为, 形成一个预测模型, 该模型能对新数据进行预测并向用户进行结果推荐.
推荐系统往往希望从用户那里获取更多个人信息, 以此来实现更优质的推荐服务, 但随之而来的隐私泄露问题也越来越显著[7-10].用户在向推荐系统提交数据的时候不希望敏感信息泄露, 因此隐私保护成为推荐系统关注和研究的重点.
为实现隐私保护, 随机扰动技术(Randomized Perturbation Techniques, RPT)[11]允许用户伪装自己的真实数据, 即在真实数据后加上一个伪随机数再发送给推荐系统.匿名方法也可实现保护隐私, 即允许一个用户拥有多个身份.
本文利用脊回归[17]对单个用户的大量数据进行回归计算, 使用Yao的混淆电路技术, 实现用户对云端计算出的推荐模型的正确性验证, 使用一种新的具有全同态性质的数据聚合方法AGG[16], 来替换大多数已有方案中所使用的同态加密方法.本文结合混淆电路与AGG方法, 能在保证用户输入输出隐私前提下实现用户对云端计算出的推荐模型的正确性验证, 并且能减少用户和云端的资源开销.
1 网络架构本文用到的符号说明如下: [
系统网络架构如图 1所示, 主要由数据拥有者(
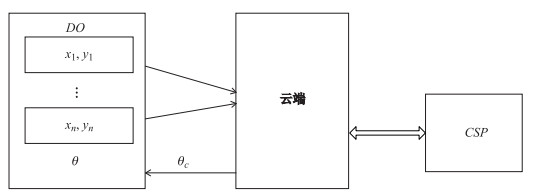
|
图 1 系统网络架构 Fig.1 Network architecture of the system |
脊回归是一种适用于共线性数据分析的有偏估计回归方法, 通过对最小二乘法的损失函数增加一个正则化项, 使得回归系数更可靠, 能对高维数据进行处理, 可应用于机器学习领域.
多元线性回归中, 令
求解函数
| $ \begin{equation} \label{eq1} F(\theta )=\sum\nolimits_{i=1}^n {(y_i -\theta ^{\text{T}}x_i )^2} +\lambda \left\| \theta \right\|_2^2, \end{equation} $ | (1) |
而最小化损失函数
对于线性回归模型
| $ \begin{equation} \label{eq2} A\theta =b, \end{equation} $ | (2) |
其中,
混淆电路(Garbled Circuits)是Andrew Yao教授于1982年为解决安全多方计算问题而提出的一个概念.在两方计算中, Yao的混淆电路允许分别拥有隐私数据
协议执行过程如下:
2取1不经意传输协议:不经意传输协议是一个选择方
本文中, 混淆电路构造者即加密服务提供者, 推荐系统由云端充当.
加密服务提供者把外包计算函数
| $ \begin{align} r_{00} =E_{w_i^0 } (E_{w_j^0 } (w_k^{g^{(0, 0)}} )), \quad r_{01} =E_{w_i^0 } (E_{w_j^1 } (w_k^{g^{(0, 1)}} )), \end{align} $ | (3) |
| $ \begin{align} r_{10} =E_{w_i^1 } (E_{w_j^0 } (w_k^{g^{(1, 0)}} )), \quad r_{11} =E_{w_i^1 } (E_{w_j^1 } (w_k^{g^{(1, 1)}} )), \end{align} $ | (4) |
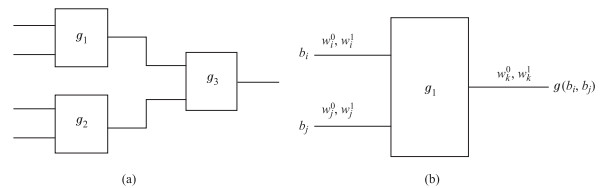
|
图 2 混淆电路 Fig.2 Example of a garbled gate |
其中
因为每个门的4个密文均采用随机排列, 即第一个密文
云端接收到数据拥有者发送过来的密文数据后, 和加密服务提供者进行一系列交互, 获得混淆电路以及密文数据得混淆电路输入形式.对于电路中的一个门, 比如
大整数分解问题, 即每个正整数
| $ \begin{align} N=p_1^{\alpha _1 } p_2^{\alpha _2 } \cdot \cdot \cdot p_s^{\alpha _s }, \quad \alpha _{\text{i}} >0, \quad i=1, \cdots, s, \end{align} $ | (5) |
其中
给定2个大素数
| $ \begin{equation} {\text{Adv}}_A^{\text{IFP}} ={\text{Prob}}\left[{s\leftarrow A(N)\wedge (s\in \{p, q\})} \right]\le {\text{negl}}(\lambda ). \end{equation} $ | (6) |
本文中第3.1节AGG算法的安全性是基于大整数分解难题假设的.由于云端只知道公开的大整数
可验证外包计算由以下4个算法组成(KeyGen, ProbGen, Compute, Verify).
(1) KeyGen
(2) ProbGen(
(3) Compute(
(4) Verify
可验证外包计算方案(
定义1(正确性) 对于任意的外包函数
若恶意的云端不能让验证算法Verify接受一个错误的结果, 即给出外包函数
具体的安全性博弈
| $ (PK, SK)\buildrel R \over \longleftarrow {\text{KeyGen}}(f, \lambda ), $ |
对于
| $ \begin{align*} x_i &\leftarrow A(PK, x_1, \sigma _1, \cdots, x_i, \sigma _i ), \\ (\sigma _i, \tau _i )&\leftarrow {\text{ProbGen}}(SK, x_i ), \\ (i, \hat {\sigma }_y )&\leftarrow A(PK, x_1, \sigma _1, \cdots, x_q , \sigma _q ), \\ \hat {y}&\leftarrow {\text{Verify}}(SK, \tau _i, \hat {\sigma }_y ), \end{align*} $ |
如果
定义2(安全性) 若对于任意概率多项式时间(
| $ \begin{equation} \label{eq5} {\text{Adv}}_{A, VC}^{\text{Verif}} (f, \lambda )={\text{Prob}}\left[{{\text{Game}}_{A, VC}^{\text{Verif}} (f, \lambda )=1} \right]\le {\text{negl}}(\lambda ), \end{equation} $ | (7) |
即让验证算法Verify接受一个错误的结果的概率是可忽略的, 此时则可说明可验证外包计算方案是安全的.式(7)中
可验证外包计算使得数据能够被正确计算, 但在云计算中, 数据拥有者的输入输出隐私也需要得到保护.在这里输入数据的隐私由Game
| $ \begin{align*} (PK, SK)&\buildrel R \over \leftarrow {\text{KeyGen}}(f, \lambda ), \\ (x_0, x_1 )&\leftarrow A^{O^{{\text{ProbGen}}(SK, \cdot )}}(PK), \\ (\sigma _0, \tau _0 )&\leftarrow {\text{ProbGen}}(SK, x_0 ), \\ (\sigma _1, \tau _1 )&\leftarrow {\text{ProbGen}}(SK, x_1 ), \\ b&\buildrel R \over \leftarrow \{0, 1\}, \\ {b}'&\leftarrow A^{O^{{\text{ProbGen}}(SK, \cdot )}}(PK, x_0, x_1 , \sigma _b ), \end{align*} $ |
其中
如果
定义3(隐私性) 若对于任意概率多项式时间(
| $ \begin{equation} \label{eq6}{\text{Adv}}_{A, VC}^{\text{Priv}} (f, \lambda )=\left| {{\text{Prob}}\left[{{\text{Game}}_{A, VC}^{\text{Priv}} (f, \lambda )=1} \right]-\frac{1}{2}} \right|\le {\text{negl}}(\lambda ), \end{equation} $ | (8) |
则说明可验证外包计算方案是隐私保护的.式(8)中
如图 3所示, 系统主要由数据拥有者(
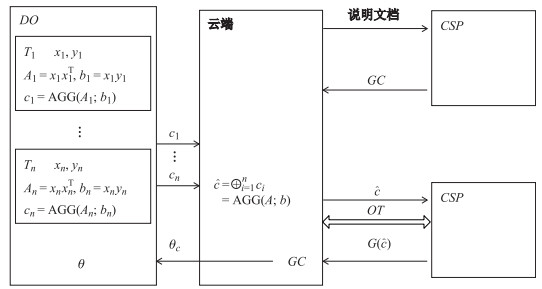
|
图 3 系统详述 Fig.3 High-level description of the system |
方案具体过程如下.
首先, 云端向
其次, 对于第
云端输入
隐私保护数据聚合算法AGG是一种对称同态加密方法, 支持密文域上的加法和乘法运算, 可用于替换公钥全同态加密算法, 主要应用在用户对数据的加密处理以及云端计算混淆电路过程中.第3.2节可验证外包计算方案中有可验证外包计算算法调用AGG算法的具体步骤. AGG主要由AGG.KGen, AGG.Enc, AGG.Eval, AGG.Dec等4个算法组成.
(1) AGG.KGen:输入安全参数
(2) AGG.Enc:数据拥有者随机选择2个位数为
对于第
| $ \begin{equation} \label{eq7} m_{i, p} \equiv m_i \bmod p, \quad m_{i, q} \equiv m_i \bmod q, \end{equation} $ | (9) |
其中,
| $ \begin{equation} \label{eq8} 1\equiv q^{-1}q\bmod p, \quad 1\equiv p^{-1}p\bmod q. \end{equation} $ | (10) |
数据拥有者计算密文分量
| $ c_{1, i} =q^{-1}qm_{i, p}^p +p^{-1}pm_{i, q}^q +U_i^{\text{add}} \bmod N, $ | (11a) |
| $ c_{2, i} =(q^{-1}qm_{i, p}^p +p^{-1}pm_{i, q}^q )U_i^{\text{mul}} \bmod N. $ | (11b) |
当对
| $ \begin{equation} U_T^{\text{add}} =\sum\limits_{i=1}^{d^2+d} {U_i^{\text{add}} } \bmod N, \quad U_T^{\text{mul}} =\sum\limits_{i=1}^{d^2+d} {U_i^{\text{mul}} } \bmod N, \end{equation} $ | (12) |
然后计算密文
| $ \begin{align*} c_i =(c_{1, i}, c_{2, i}, c_{\text{ram}}^{\text{add}}, c_{\text{ram}}^{\text{mul}} ), \end{align*} $ |
其中,
| $ \begin{align*} c_{\text{ram}}^{\text{add}} =H_0 (p\parallel U_T^{\text{add}} ), \quad c_{\text{ram}}^{\text{mul}} =H_0 (p\parallel U_T^{\text{mul}}). \end{align*} $ |
(3) AGG.Eval:云端收集完
| $ c_T^{\text{add}} =\sum\limits_{i=1}^{d^2+d} {c_{1, i} } -U_T^{\text{add}} \mod N \notag\\ \ \ \ \ =q^{-1}q\sum\limits_{i=1}^{d^2+d} {m_{i, p}^p } +p^{-1}p\sum\limits_{i=1}^{d^2+d} {m_{i, q}^q }\!\!\!\!\!\mod N \notag\\ \ \ \ \ =q^{-1}q\Big(\sum\limits_{i=1}^{d^2+d} {m_{i, p}}\Big)^p +p^{-1}p\Big(\sum\limits_{i=1}^{d^2+d} {m_{i, q}}\Big)^q\!\!\!\!\!\mod N, $ | (13a) |
| $ c_T^{\text{mul}} =\mathop \prod \limits_{i=1}^{d^2+d} c_{2, i} (U_T^{\text{mul}} )^{-1}\bmod N \notag\\ \ \ \ \ =\mathop \prod \limits_{i=1}^{d^2+d} (q^{-1}qm_{i, p}^p +p^{-1}pm_{i, q}^q )\!\!\!\!\!\mod N\notag \\ \ \ \ \ =q^{-1}q\Big(\mathop \prod \limits_{i=1}^{d^2+d} m_{i, p} \Big)^p +p^{-1}p\Big(\mathop \prod \limits_{i=1}^{d^2+d} m_{i, q} \Big)^q\!\!\!\!\!\mod N, $ | (13b) |
| $ c_3^\theta =H_1 (\theta _c \parallel c_{\text{ram}}^{\text{add}} \parallel c_{\text{ram}}^{\text{mul}}). $ | (13c) |
同时把计算结果
(4) AGG.Dec:数据拥有者接收到云端发送过来的数据后, 验证
| $ \begin{align*} c_{\text{ram}}^{\text{add}} =\, &H_0 (p\parallel U_T^{\text{add}} ), \\ c_{\text{ram}}^{\text{mul}} =\, &H_0 (p\parallel U_T^{\text{mul}} ), \\ c_3^\theta =\, &H_1 (\theta _c \parallel c_{\text{ram}}^{\text{add}} \parallel c_{\text{ram}}^{\text{mul}} ) \end{align*} $ |
是否成立, 若不成立则输出终止符
| $ \theta _c \bmod p=\theta _{c, p} \bmod p, $ | (14a) |
| $ \theta _c \bmod q=\theta _{c, q} \bmod q. $ | (14b) |
| $ c_T^{\text{add}} \!\!\!\!\!\mod p=q^{-1}q\Big(\sum\limits_{i=1}^{d^2+d} {m_{i, p}} \Big)^p\!\!\!\!\!\mod p=\sum\limits_{i=1}^{d^2+d} {m_{i, p}} \!\!\!\!\!\mod p, $ | (15a) |
| $ c_T^{\text{add}} \!\!\!\!\!\mod q=p^{-1}p\Big(\sum\limits_{i=1}^{d^2+d} {m_{i, q}} \Big)^q\!\!\!\!\!\mod q=\sum\limits_{i=1}^{d^2+d} {m_{i, q} } \!\!\!\!\!\mod q, $ | (15b) |
| $ c_T^{\text{mul}} \!\!\!\!\!\mod p=q^{-1}q\Big(\mathop \prod \limits_{i=1}^{d^2+d} m_{i, p} \Big)^p\!\!\!\!\!\mod p=\mathop \prod \limits_{i=1}^{d^2+d} m_{i, p} \!\!\!\!\!\mod p, $ | (15c) |
| $ c_T^{\text{mul}} \!\!\!\!\!\mod q=p^{-1}p\Big(\mathop \prod \limits_{i=1}^{d^2+d} m_{i, q} \Big)^q\!\!\!\!\!\mod q=\mathop \prod \limits_{i=1}^{d^2+d} m_{i, q} \!\!\!\!\!\mod q. $ | (15d) |
公式(15)中, 用户对公式(13)中云端计算出的信息进行模
| $ \begin{equation} \theta_c'=qM_p'\theta _{c, p}+pM_q' \theta _{c, q} \bmod N, \end{equation} $ | (16) |
其中,
| $ M_p' q=1\bmod p, $ | (17a) |
| $ M_q' p=1\bmod q. $ | (17b) |
最后可利用可验证外包计算方案中的
可验证外包计算方案调用了第3.1节介绍的数据加密方法AGG, 由以下4个算法组成(KeyGen, ProbGen, Compute, Verify).
(1) KeyGen
(2) ProbGen
(3) Compute
(4) Verify
如文献[15]中介绍, 电路中使用的对称加密算法
本文方案中, 需要把第3.1节数据加密算法的加法以及乘法同态性质应用到机制
Yao的混淆电路方案是可证明安全的[16], 在这里对本文第3.1节数据加密方法的安全性进行分析.
输入数据隐私性:数据拥有者加密处理自身数据为
| $ \begin{align*} c_{1, i} =q^{-1}qm_{i, p}^p +p^{-1}pm_{i, q}^q +U_i^{\text{add}} \bmod N, \quad c_{2, i} =(q^{-1}qm_{i, p}^p +p^{-1}pm_{i, q}^q )U_i^{\text{mul}} \bmod N. \end{align*} $ |
密文
输出数据隐私性:假设有一个敌手
本文中AGG算法使用的是对称同态映射, 即加密和解密使用的都是相同的密钥
本文提出了一个实现高效可验证的隐私保护推荐系统的3方模型, 即数据拥有者、加密服务提供者、云端的3方模型.在保护数据隐私的同时实现用户对云端计算出的推荐模型的正确性验证, 并且利用一个新的数据处理方法AGG代替全同态加密, 提高了系统效率.
本文方案目前是针对单个用户数据进行计算, 如何同时对多用户数据进行计算是今后要研究的课题之一.
| [1] | ZHAO Z D, SHANG M S. User-based collaborative-filtering recommendation algorithms on hadoop[C]//Knowledge Discovery and Data Mining, WKDD'10, 3rd International Conference on. IEEE, 2010: 478-481. |
| [2] | 邓爱林, 朱扬勇, 施伯乐. 基于项目评分预测的协同过滤推荐算法[J]. 软件学报, 2003, 14(9): 1621-1628. |
| [3] | SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. ACM, 2001: 285-295. |
| [4] | PAVLOV D, PENNOCK D M. A maximum entropy approach to collaborative filtering in dynamic, sparse, high-dimensional domains[C]//NIPS. 2002, 2: 1441-1448. |
| [5] | MARLIN B M. Modeling user rating profiles for collaborative filtering[C]//Advances in Neural Information Processing Systems. 2004: 627-634. |
| [6] | NIKOLAENKO V, IOANNIDIS S, WEINSBERG U, et al. Privacy-preserving matrix factorization[C]//Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security. ACM, 2013: 801-812. |
| [7] | SHYONG K, FRANKOWSKI D, RIEDL J. Do you trust your recommendations? An exploration of security and privacy issues in recommender systems[M]//Emerging Trends in Information and Communication Security. Berlin: Springer, 2006: 14-29. |
| [8] | AÏMEUR E, BRASSARD G, FERNANDEZ J M, et al. Alambic:A privacy-preserving recommender system for electronic commerce[J]. International Journal of Information Security, 2008, 7(5): 307-334. DOI:10.1007/s10207-007-0049-3 |
| [9] | MCSHERRY F, MIRONOV I. Differentially private recommender systems: Building privacy into the net[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2009: 627-636. |
| [10] | MOBASHER B, BURKE R, BHAUMIK R, et al. Toward trustworthy recommender systems:An analysis of attack models and algorithm robustness[J]. ACM Transactions on Internet Technology (TOIT), 2007, 7(4): 23-38. DOI:10.1145/1278366 |
| [11] | POLAT H, DU W. Privacy-preserving collaborative filtering using randomized perturbation techniques[C]//IEEE Internatioal Conference on Data Mining. IEEE, 2005: 625-628. |
| [12] | GENTRY C. Fully homomorphic encryption using ideal lattices[C]//Proceedings of the 41st Annual ACM Symposium on Theory of Computing. 2009: 169-178. |
| [13] | YAO A C C. Protocols for secure computations[C]//Foundations of Computer Science, 1982, SFCS'08, 23rd Annual Symposium on. IEEE, 1982: 160-164. |
| [14] | YAO A C C. How to generate and exchange secrets[C]//Foundations of Computer Science, 1986, 27th Annual Symposium on. IEEE, 1986: 162-167. |
| [15] | GENNARO R, GENTRY C, PARNO B. Non-interactive verifiable computing: Outsourcing computation to untrusted workers[C]//Annual Cryptology Conference. Berlin: Springer, 2010: 465-482. |
| [16] | ZHOU J, CAO Z F, DONG X L, et al. Security and privacy for cloud-based IoT:Challenges[J]. IEEE Communications Magazine, 2017, 55(1): 26-33. DOI:10.1109/MCOM.2017.1600363CM |
| [17] | NIKOLAENKO V, WEINSBERG U, IOANNIDIS S, et al. Privacy-preserving ridge regression on hundreds of millions of records[C]//Security and Privacy (SP), 2013 IEEE Symposium on. IEEE, 2013: 334-348. |
| [18] | PAILLIER P. Public-key cryptosystems based on composite degree residuosity classes[C]//International Conference on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 1999: 223-238. |




