近些年, 随着移动通信技术的高速发展和智能设备的普及, 基于位置的服务已经广泛应用于人们的日常生活中.研究人员利用人们随身携带的智能设备, 如智能手机、智能手表和一些具有定位功能的设备等, 获取这些设备生成的位置信息, 提供给携带者所需要的各种基于所在位置的服务[1-2].在众多服务之中, 旅行规划问题是一个研究热点问题.在决定去往旅游地之前, 人们总是需要作一份旅行规划.由于兴趣点的数量众多、游客的时间有限、对不同的兴趣点类型喜好不同, 游客因此需要从大量的兴趣点集合中选择出自己感兴趣的兴趣点.为此他们需要比较兴趣点的类型、位置信息以及该兴趣点的受欢迎度等, 除此之外, 还要考虑兴趣点的游玩顺序.
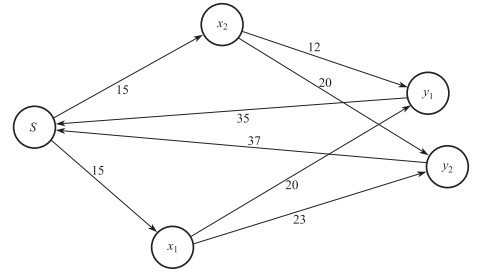
在旅行规划中, 游客首先需要考虑的一个问题就是如何选择自己偏爱的兴趣点.目前, 已经有很多工作研究了如何针对不同的游客推荐给他们可能感兴趣的兴趣点.其中, 一些研究使用一片区域内人群和出租车生成的GPS轨迹信息, 发掘出该区域内有意思的地点和交通信息[3-4].在其他的研究中, 研究人员使用具有定位功能的照片来帮助游客进行兴趣点的选择[5-6].除此之外, 使用来自基于位置的社交服务所产生的数据也可以给游客推荐合适的信息[7].因此, 通过以上这些方面的工作, 游客可以获取他们可能感兴趣的地点.在推荐了合适的兴趣点之后, 旅行规划的第二个问题就是找到一条合适的路线遍历这些兴趣点.在这一方面, 同样有不同的工作对此展开研究.在之前的一些研究中, 研究人员在路线兴趣点的添加中主要考虑距离以及交通的影响, 目的是找到一条距离最短路线[8-10], 或者是在时间限制下游玩更多的景点[11-12].但是在这一情形下, 旅行规划则忽略了兴趣点本身的质量, 因此很难找到质量高的兴趣点.在其他的一些研究中, 研究人员不仅考虑了兴趣点之间的距离, 也在路线兴趣点的添加中考虑了这些景点的质量, 如评分、受欢迎度等[13-14].然而, 目前几乎没用相关研究考虑到游客可能在旅游地不止停留一天.在多日旅行规划中, 规划路线的情形将与之前的研究工作有所不同, 我们用图 1示例说明.
|
图 1 多日旅行规划示例 Fig.1 A example of multi-day trip planning |
如图, 我们假定游客的2 d游行程规划为从
本文研究了多日的旅行规划问题.游客在规划的开始阶段选择自己的旅行天数、感兴趣的类别, 决定这些兴趣点类别的游玩顺序.多日旅行规划根据游客选择的类别为游客推荐合适的候选兴趣点.为了保证规划路线距离以及线路中兴趣点的质量要求, 我们从这些候选兴趣点中找到最合适的多日旅行路线.本文的主要贡献可以归为以下3点.
(1) 考虑了多日旅行规划问题.当游客在所在城市游玩多日时, 之前的旅行规划方式不适合多日情形下的旅行规划.
(2) 在多日旅行规划中需要考虑多日旅行满意度的稳定性问题.游客在多日的游玩中需要得到均衡的高质量旅行规划路线.
(3) 提出了全新的启发式方法用于规划路线.通过实验证明, 我们的方法可以得到均衡的高质量多日旅行路线.
本文的其他部分结构是:第1节介绍旅行规划的相关工作; 第2节具体描述多日旅行规划问题; 第3节提出3种启发式算法用于得出多日旅行规划路线; 第4节为实验的结果以及分析; 第5节是结论以及未来工作.
1 相关工作旅行规划问题在近些年已经得到了广泛的研究, 在商业领域也得到充分的发展.在设计旅行规划路线时, 研究人员首先需要为游客推荐他们可能喜爱的兴趣点, 这一部分需要来自游客自身的个性化信息, 以此来分析游客的个人偏好; 然后整合所推荐的兴趣点, 这一部分不仅需要考虑兴趣点的信息还要分析所在地的交通信息, 才能规划出符合条件的旅行路线.
旅行规划的第一步是兴趣点的选择.基于位置的服务的普及为研究人员提供了大量可利用的数据信息.在文献[3]中, Zheng等人利用来自不同移动设备的GPS轨迹信息, 挖掘出在一片区域内有趣的地点并提供给游客.同时, 人们也可以通过出租车的GPS信息来获得旅行推荐[4].近些年, 更多的研究集中在搜索大量具有地理位置的标签照片来生成有效数据.通过地理标签照片, 研究人员可以挖掘出有兴趣的地点, 并推荐给游客.例如, 在文献[5-6, 15]中, 研究人员收集大量来自社交软件的地理标记照片, 如Foursquare、Gowalla、Flickr等, 在这些社交软件中, 人们通过分享具有地理标记的照片来进行社交联系.从这些照片可以得到充分的关于兴趣点相关信息(位置、人流量、受欢迎度以及合适的停留时间等)的数据, 为游客推荐他们可能喜欢的兴趣点.除此之外, 还有一些研究的推荐兴趣点方法里同时考虑到了人群之间社交关系对兴趣点选择的影响, 如文献[7]中, 研究人员认为游客在选择兴趣点时会更有可能选择自己的好友所分享的兴趣点, 以及在社交软件中关注的人所去过的地方.
在选择了兴趣点之后, 需要考虑如何把这些兴趣点规划成有效的旅行路线, 通过路径搜索算法, 找到最佳的旅行路线.目前已经有研究人员提出了不同的路径搜索算法.在最早的研究中, 研究人员将旅行路线的搜索规划为旅行商问题, 并使用相关的线路搜索算法.之后在研究中, Li等人[8]研究了一种新的旅行线路类型TPQ (Trip Planning Query), 将所有的兴趣点归到特定的类别, 使用一系列不同近似比的近似算法, 从出发地到目的地, 找到一条至少每个类别兴趣点访问一次的最佳路线.除此之外, 其他研究人员也考虑了兴趣点的访问次序问题.在Sharifzadeh等人提出的OSR (Optimal Sequenced Route)中[9], 使用轻量级基于阈值的迭代算法用于搜索最佳路线, 不同于文献[8], 他们认为游客在规划路线时可能会以某种次序访问其中的一些兴趣点.在其他的一些研究中[16-18], 研究人员通过限定部分兴趣点类别的顺序, 并使用不同的启发式算法来进行路线搜索.
除了搜索最短路径, 研究人员在路线规划中还考虑了兴趣点的受欢迎度以及旅行时限问题.通过将受欢迎度转换为评分, 在路径搜索中找到距离和评分都符合条件的兴趣点. Chen等人[19]根据兴趣点的人流量以及游客对兴趣点类别的主观偏好, 给所有的兴趣点进行评分, 在之后的路线搜索中, 通过启发式算法将其中最符合评分距离比的兴趣点添加到旅行路线中. Dai等人[13]提出了另外一种旅行规划模型, 在所有兴趣点的平均分大于给定值的情况下, 旅行线路的用时最短, 在搜索兴趣点上, 他们使用3种近似算法并得到了有效的旅行路线.除此之外, 还有一些其他的线路规划则考虑了时间限制. Lu等人[14]在算法上使用了3种优化机制来提高旅行路线的搜索效率. Bao等人[20]提出了在特定时间限制下的基于贪心策略的旅行规划算法, 他们研究了在时间条件限制下如何从现有的旅行线路中选择合适的子集路线.不同于以上这些工作, 本文研究的是多日旅行规划问题, 所以以上这些研究并不适用于多日旅行规划的解决, 需要制订多天的旅行线路并且要使多天的旅行线路服务质量保持稳定.
2 问题定义在本节中, 首先介绍和定义本文研究所需要的一些相关变量, 然后提出研究目标. 表 1总结了本文所用的参数.
| 表 1 路径规划参数 Tab.1 Attributes of path planning |
定义1 兴趣点集
定义2 路线集
定义3 单日旅行
定义4 多日旅行
定义5 旅行线路消耗时间指的是1 d的兴趣点游玩所需要的时间, 该时间由所有兴趣点的停留时间之和加上兴趣点之间转移所耗费的交通时间之和组成.用单日旅行时间
| $ \begin{align*} t(tp)=t(s, a_{k_1})+\sum\limits^{n}_{i=1}t(a_{k_1})+\sum\limits^{n-1}_{i=1}t(r_{k_i, k_{i+1}})+t(a_{k_n}, s), \end{align*} $ |
其中,
| $ \begin{align*} T(tp)=\sum\limits^{D}_{i=1}t(tp_i). \end{align*} $ |
定义6 旅行线路评分是由该天所有兴趣点的评分之和组成.当一条单日旅行线路为
| $ \begin{align*} s(tp)=\sum\limits^{n}_{i=1}s(a_{k_i}). \end{align*} $ |
用
| $ \begin{align*} S(tp)=\sum\limits^{D}_{i=1}s(tp_i). \end{align*} $ |
研究目标:为游客制订多日旅行线路.一个有效的多日旅行规划需要游客预先指定以下信息.
(1) 指定的出发地和目的地.在多日旅行规划中, 出发地和目的地相同.
(2) 游客指定的兴趣点类型游玩顺序
(3) 游客指定的游玩天数
为了能够确定多日旅行规划的优劣, 使用旅行效益来衡量多日旅行规划的好坏, 并用符号
| $ \begin{align} U=S(tp)-\lambda\times \sigma. \end{align} $ | (1) |
式(1)中
将兴趣点分成不同的类型, 在游客指定完出发点和兴趣点类别的游玩顺序后, 通过游客决定的类别游玩顺序来为游客选择最佳的线路规划.首先计算使用穷举法的问题复杂度.假定在第
| $ \begin{align*} O=D\times(m+1)\times \prod\limits^{m}_{i=1}c_i. \end{align*} $ |
由此可知当兴趣点的数量变化时, 需要的计算时间和空间将会呈指数式增长, 所以利用穷举法来解决此问题并不现实.因此我们决定使用其他的方法来解决本问题.在本节中, 我们提出了3种启发式算法用于得到最佳旅行路径.
(1) 评分最高添加算法, 见算法1.首先按照兴趣点的评分高低来选择, 根据游客选择的兴趣点类别和游玩顺序, 再从确定好的兴趣点类别访问顺序中选择合适的兴趣点.在本算法中, 我们逐天完成旅行线路中兴趣点的添加.首先, 初始化行程和每天的起点(行1-4), 之后逐天添加兴趣点(行5-9)在第一天里, 分别选择每一类中评分最高的兴趣点(行7), 添加完成之后作为第一天的旅行线路, 并在候选兴趣点中删除(行9).到了第二天, 从每一类别中选择已经游玩之外的兴趣点中评分最高的兴趣点作为这天的旅行路线.同理, 完成剩余天数的旅行线路添加.最后返回
| 算法1评分最高添加 |
| 输入: 出发地点 |
| 输出: |
| 1. |
| 2. for |
| 3. |
| 4. end for |
| 5. for |
| 6. for |
| 7. tempPOI //将 |
| 8. |
| 9. Delete tempPOI //将已经选择的兴趣点排除候选兴趣点集 |
| 10. return |
(2) 同步评分最高添加算法, 见算法2.不同于算法1, 为了保证多日旅行满意度的稳定性, 我们采取同步策略来添加兴趣点.通过游客确定好的兴趣点的类型以及游玩顺序, 同步完成
| 算法2 同步评分最高添加 |
| 输入:出发地点 |
| 输出: |
| 1. |
| 2. for |
| 3. |
| 4. end for |
| 5. while (POIType== |
| 6. for |
| 7. tempPOI |
| 8. |
| 9. Delete tempPOI |
| 10. end while |
| 11. for |
| 12. //将 |
| 13. for |
| 14. tempPOI //将 |
| 15. |
| 16. Delete tempPOI |
| 17. return |
(3) 同步评分时间添加算法.通过算法2, 基本可以得到多条满意度均衡的旅行线路.然而, 在添加兴趣点时由于只考虑了兴趣点的评分因素, 导致可能出现游玩该线路兴趣点所耗交通时间过长, 然而游客一般不会选择一条交通时间过长的旅行线路.为了使旅行线路更为优化, 我们通过计算兴趣点的评分和兴趣点之间交通时间的比值来得出最佳的兴趣点添加策略.假设已选择类型
通过具体的实验来测试本文所提出的方法, 利用人工数据来验证方法的具体结果.
实验设置.选择上海作为旅游地点, 使用某旅行网中的景点推荐栏目获取游客可能游览的兴趣点集.在本次实验中, 根据兴趣点的性质, 如自然、人文等, 将所有的兴趣点分为10种类型, 在考虑到每种类型中兴趣点的人流量和受欢迎程度后, 去除一些质量较差的兴趣点, 确定每种类型的兴趣点数为20.通过谷歌地图搜索, 可以知道兴趣点之间的交通距离.之后, 对兴趣点进行评分(从0到10), 使用某旅行网中游客兴趣点的签到数据来统计该兴趣点的人流量, 利用游客的评价信息来统计兴趣点的受欢迎度.通过人流量和受欢迎度两项指标计算出每一个兴趣点的评分.在计算多日旅行效益值时, 需要计算旅行兴趣点总评分以及
实验分析.多日旅行规划中3种算法的效果取决于两个因素:首先是兴趣点数量的变化, 当游客选择兴趣点的类型数量不同或者是兴趣点类型中兴趣点的数量变化时, 都会影响候选兴趣点的变化; 其次, 游客选择的旅行天数不同也会使算法选择不同的旅行线路.
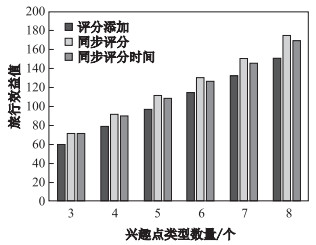
首先研究兴趣点数量的变化.为了简化实验, 设置每一类型兴趣点的数量为20, 通过兴趣点类型变化, 来改变整体兴趣点的数量.假设旅行天数
|
图 2 旅行效益值/类型数量关系图 Fig.2 Trip score by varying number of POI types |
|
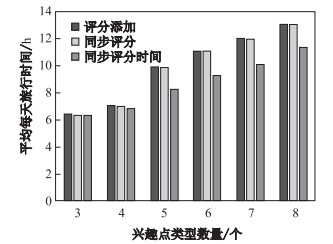
图 3 平均每天旅行时间/类型数量关系图 Fig.3 Average per day trip time by varying number of POI types |
|
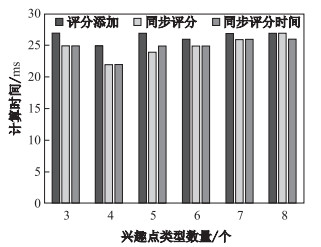
图 4 计算时间/类型数量关系图 Fig.4 Computation time cost by varying number of POI types |
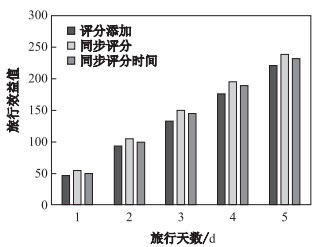
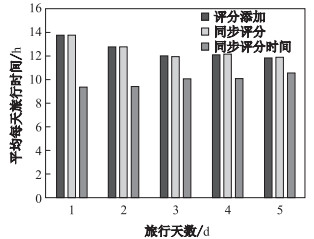
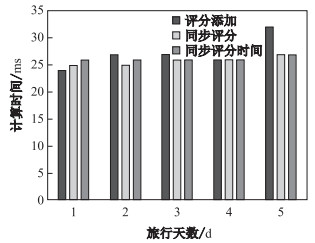
在实验中, 同时研究了旅行天数的变化对旅行效益值的影响.在研究天数变化时, 设定每日旅行兴趣点类别数量为7, 在图 5中, 显示了游客在选择旅行天数从第一天到第五天时, 旅行效益值的变化, 可以看出随着天数增多, 旅行效益值也增大.这是因为在天数增多时游客可以游览更多的兴趣点, 使得旅行效益值更大.算法2和同步评分时间添加算法能够使游客获得更多的旅行效益.在图 6中, 实验显示了3种算法的旅行线路平均每天所需旅行时间, 结果表明同步评分时间添加算法相比前两种算法可以使游客更为节省时间. 图 7则是在旅行天数变化时, 3种算法搜寻旅行线路所需时间.
|
图 5 旅行效益值/旅行天数关系图 Fig.5 Trip score by varying trip days |
|
图 6 平均每天旅行时间/旅行天数关系图 Fig.6 Average per day trip time by varying trip days |
|
图 7 计算时间/旅行天数关系图 Fig.7 Computation time cost by varying trip days |
本文研究推导出了一种新的旅行规划方式, 即多日旅行规划.在多日旅行规划中, 考虑了游客在多日旅行中满意度的稳定性问题, 提高了游客多日旅行的旅行质量.在选择旅行线路时, 提出了3种启发式算发, 3种算法都能够在短时间内规划出多日旅行路线, 其中同步评分最高添加算法和同步评分时间添加算法可以得到更高的旅行效益值, 同步评分时间添加算法则可以使游客节省更多的时间.
在以后的工作中, 我们会在多日旅行规划中考虑游客对时间限制的要求, 研究在动态的交通变化中, 如何更好地规划旅行路线.
| [1] | WANG H Y, QIAN J. Geographic location-based service reliability prediction[C]//Proceedings of the 20142nd International Conference on Advanced Cloud and Big Data. 2014: 267-274. |
| [2] | JIANG L C, YUE P, GUO X. Semantic location-based services[C]//Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium. IEEE Xplore, 2016: 3606-3609. |
| [3] | ZHENG Y, ZHANG L Z, XIE X, et al. Mining interesting locations and travel sequences from GPS trajectories[C]//International Conference on World Wide Web. 2009: 791-800. |
| [4] | BALAN R K, NGUYEN K X, JIANG L. Real-time trip information service for a large taxi fleet[C]//International Conference on Mobile Systems. 2011: 99-112. |
| [5] | YIN H G, WANG C H, YU N H, et al. Trip mining and recommendation from geo-tagged photos[C]//Proceedings of the 2012 IEEE International Conference on Multimedia and Expo Workshops. IEEE Xplore, 2012: 540-545. |
| [6] | ARASE Y, XIE X, HARA T, et al. Mining people's trips from large scale geo-tagged photos[C]//International Conference on Multimedea. 2010: 133-142. |
| [7] | NOULAS A, SCELLATO S, LATHIA N, et al. A random walk around the city: New venue recommendation in location-based social networks[C]//Proceedings of the 2012 International Conference on Privacy, Security, Risk and Trust and 2012 International Conference on Social Computing. 2012: 144-153. |
| [8] | LI F F, CHENG D H, HADJIELEFTHERIOU M, et al. On trip planning queries in spatial databases[C]//Proceedings of the 9th International Conference on Advances in Spatial and Temporal Databases. 2005: 273-290. |
| [9] | SHARIFZADEH M, KOLAHDOUZAN M, SHAHABI C. The optimal sequenced route query[J]. The VLDB Journal, 2008, 17(4): 765-787. DOI:10.1007/s00778-006-0038-6 |
| [10] | NUZZOLO A, COMI A, ROSATI L. Normative optimal strategies: A new approach in advanced transit trip planning[C]//Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems. 2016: 35-40. |
| [11] | CHIA W C, YEONG L S, LEE F J X, et al. Trip planning route optimization with operating hour and duration of stay constraints[C]//Proceedings of the 201611th International Conference on Computer Science & Education. 2016: 395-400 |
| [12] | LOPES R B, COELHO T, SANTOS B S. Visually supporting location and routing decisions in tourist trip planning: An exploratory approach[C]//Proceedings of the 201620th International Conference Information Visualization. 2016: 236-241. |
| [13] | DAI J Q, LIU G F, XU J J, et al. An efficient trust-oriented trip planning method in road networks[C]//Proceedings of the 2014 IEEE 11th Intl Conf on Ubiquitous Intelligence and Computing and 2014 IEEE 11th Intl Conf on Autonomic and Trusted Computing and 2014 IEEE 14th Intl Conf on Scalable Computing and Communications and Its Associated Workshops. 2014: 487-494. |
| [14] | LU E H C, LIN C Y, TSENG V S. Trip-mine: An efficient trip planning approach with travel time constraints[C]//Proceedings of the 2011 IEEE 12th International Conference on Mobile Data Management. IEEE, 2011: 152-161. |
| [15] | BRILHANTE I, MACEDO J A, NARDINI F M, et al. Where shall we go today? Planning touristic tours with TripBuilder[C]//International Conference on Information and Knowledge Management. 2013: 757-762. |
| [16] | ZHANG J Z, WEN J, MENG X F. Multi-tag route query based on order constraints in road networks[J]. Chinese Journal of Computers, 2012, 35(11): 2317-2326. DOI:10.3724/SP.J.1016.2012.02317 |
| [17] | CHEN H, KU W S, SUN M T, et al. The multi-rule partial sequenced route query[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. ACM, 2008: Article No 10. |
| [18] | KANZA Y, LEVIN R, SAFRA E, et al. Interactive route search in the presence of order constraints[J]. Proceedings of the VLDB Endowment, 2010, 3(1/2): 117-128. |
| [19] | CHEN C, ZHANG D Q, GUO B, et al. TripPlanner:Personalized trip planning leveraging heterogeneous crowdsourced digital footprints[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(3): 1259-1273. DOI:10.1109/TITS.2014.2357835 |
| [20] | BAO J L, YANG X C, WANG B, et al. An efficient trip planning algorithm under constraints[C]//Proceedings of the 201310th Web Information System and Application Conference. IEEE Xplore, 2013: 429-434. |




