2. 华东师范大学 数据科学与工程学院, 上海 200062;
3. 南京农业大学 信息科学技术学院, 南京 210095
2. School of Data Science and Engineering, East China Normal University, Shanghai 200062, China;
3. College of Information Science and Technology, Nanjing Agricultural University, Nanjing 210095, China
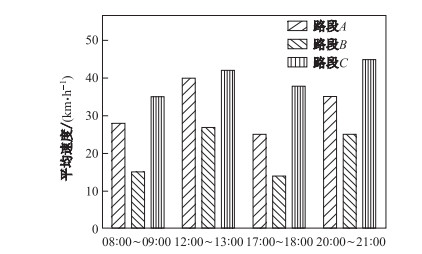
套牌车是使用违法途径盗取真牌车的号牌、型号, 使走私、拼装、报废等车辆在表面披上了"合法"的外衣.近年来, 由于机动车牌号管理不当, 套牌行为已有愈演愈烈的趋势.据报道, 在2017年3月上旬, 北京市已查处套牌违法行为371起.绝大部分套牌车没有合法的牌照, 当出现违法行为肇事逃逸时, 不仅增加了公安机构侦破难度, 而且还危害真实车主的利益, 因此, 套牌车已给社会带来巨大危害, 整治套牌车迫在眉睫.目前主要检测套牌车的途径包括硬件、软件和软硬件结合3类.基于硬件[1-2]或者软硬件结合[3]的方法能够准确地发现套牌车, 但是这些方法需要硬件支持, 成本高, 难以在现实生活中推广使用.随着车牌识别技术的完善以及卡口摄像头监控系统的普及, 以卡口时间对比法[4]为代表的软件套牌车检测技术因其成本低且实效性强的优势被广泛使用.利用时空矛盾对卡口监测数据进行处理监测时通常采用统一的速度阈值, 在阈值设置不当的情况下容易造成套牌车辆的漏检或误判.特别是当阈值设置过小时, 易将正常行驶或超速车辆误判为套牌车, 这些车辆的轨迹数据会成为噪声干扰检测结果.在实际应用中, 同一时段下的不同路段以及相同路段在不同时段下的速度分布均具有显著差异.如图 1所示,
|
图 1 不同路段不同时段车速对比示例 Fig.1 An example of speed comparison |
|
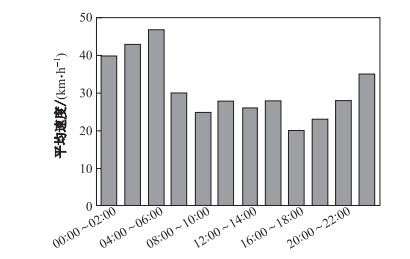
图 2 某路段车速随时间变化示例 Fig.2 An example of speed in different time |
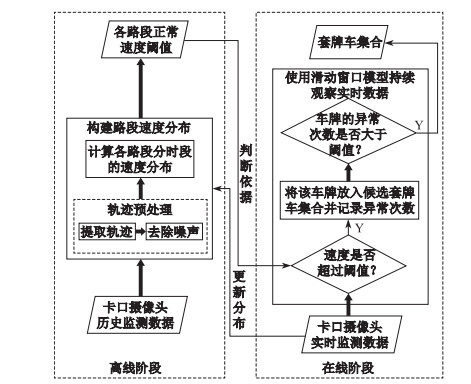
套牌车检测框架包含离线和在线两个阶段.离线阶段使用历史监测数据建立不同时段下各路段的速度分布, 确定时空限制下的速度阈值; 在线阶段根据离线阶段提取的速度阈值, 基于滑动窗口模型连续观测多个时间窗口, 将具有频繁异常行为的车辆识别为套牌车.
本文的主要贡献如下.
(1) 为及时有效地发现套牌车, 提出了基于卡口监测数据流的套牌车检测问题.
(2) 构建了一个两阶段的套牌车检测框架, 包括离线部分提取了时空限制下的路段速度阈值, 以及在线阶段通过连续监测发现具有频繁异常行为的车辆, 视其为套牌车.
(3) 基于真实的卡口监测数据集进行了大量实验, 对所提套牌车检测方法的有效性和性能进行了验证, 实验结果显示相比其他的套牌车检测方法, 本文所提方法可以有效地避免噪声数据的干扰, 实时发现套牌车辆.
本文余下部分组织为:第1节介绍相关工作; 第2节介绍问题定义与套牌车检测算法框架; 第3节详细阐述离线部分如何根据历史数据建立路段速度分布从而计算出速度阈值、在线部分如何利用路段速度阈值来建立套牌车候选集和从中筛选出套牌车; 第4节给出套牌车检测的实验结果与分析; 第5节总结全文并展望未来工作.
1 相关工作随着无线通讯技术的广泛应用, 基于位置的服务(Location-Based Service, LBS)通过无线网络使用移动对象的位置信息可以提供各类服务[5].例如利用车辆轨迹数据, 可以为用户规划合适的路径[6]、预测旅行时间[7]、发现热门路径[8]等.
作为位置服务一个新兴应用研究——套牌车检测, 其方法主要包括基于硬件、基于软件和软硬件结合3类.基于硬件方面的有:对每一个车牌边框制作独一无二的缺口和凸起[1], 从而提升车牌的防复制能力; Deng[9]提出了一种基于RFID的套牌车检测技术, 即利用RFID技术将车辆信息存储在标签中, 装有标签读取器的交通卡口可以读取标签中的车牌号并将其与卡口摄像头识别的车牌号进行比对进而检测套牌车.在硬、软件结合方面, 基于物联网的技术[3]将加密过存有车辆信息的电子标签植入机动车中, 当车辆通过被无线覆盖的基站时, 电子标签中的信息将被读取并显示在终端上, 若车辆没有安装电子标签或者电子标签中的信息与车辆不符合时, 该车被判定为套牌车并将该车辆锁定.以上基于硬件或者软硬件结合的技术能够有效准确的发现套牌车, 但是这些方法成本较高, 需要政府和车主的配合, 因此在现实生活中难以快速推广.基于软件的套牌车检测方法主要分为基于图像识别的检测以及利用卡口摄像头的监测数据来检测套牌车.基于车脸识别的套牌车检测方法[10]通过处理摄像头采集的车辆图片信息提取出车脸特征, 并将其与信息库中的车脸特征进行比对从而判断是否为套牌车.此类方法易受光线等环境因素影响, 此外, 当套牌车与原车是同一车型时无法检测出套牌车.文献[4]提出了一种基于历史车牌识别数据集的套牌车检测方法TP-Finder, 利用时空矛盾即同一个车牌不能在短时间内出现在两个距离较远的位置, 对卡口历史监测数据进行处理从而检测套牌车.该方法通过整合历史监测数据得到车牌对应的轨迹, 当检测到任意一段子轨迹的平均速度大于设定好的阈值时, 就判定该车为套牌车.基于时空矛盾的思想可以检测出部分套牌车辆, 但是不分时段对各路段使用同一速度阈值易将非法超速行驶的车辆误判为套牌车.文献[11]在此基础上提出了利用略大于极限速度的阈值来检测套牌车, 在一定程度上避免了超速车辆作为噪声数据对结果判断的影响.上述方法[5, 11]虽然可以检测出部分套牌车, 但各路段不同时段下路况不同, 不分时段的对所有路段设定统一的速度阈值, 会造成漏检许多速度并没有达到设定阈值的套牌车的后果.因此不分时段、路段仅用一个统一的阈值用于套牌车的检测并不合理.
基于时空矛盾的套牌车检测方法可视为一种轨迹异常检测.基于历史轨迹相似性的检测方法因检测精度高被广泛应用于生物、航海、路网等领域.该类方法从大规模的历史数据中挖掘轨迹的频繁模式以构建全局特征模型, 并将异于特征模型的数据判定为异常[12].文献[13]提出了一种基于船只历史轨迹数据的异常检测框架.该框架分为轨迹建模和异常检测两个阶段, 由于船只轨迹具有很大的自由度, 在轨迹建模阶段使用一个频繁区域去替代一个船只经过的位置点.通过得到的频繁区域, 将轨迹转换为一个区域序列, 利用序列获取船只的行为特征, 从而进行异常检测.文献[14]利用出租车轨迹提出了一种时间依赖的最受欢迎路线的异常检测方法.首先分时段获得的同目的地-终点的最受欢迎的K条路线, 在检测阶段, 利用两条轨迹间的编辑距离来衡量轨迹之间的差异, 如果同目的地-终点的轨迹在与该时段最受欢迎的轨迹差异明显, 将给此轨迹贴上异常的标签.使用历史轨迹构建的模型对轨迹进行异常检测时, 对模型的精确度要求很高, 利用实时采集的待检测轨迹可以增量更新已构建好的模型以提升准确率.文献[15]提出了一个交通异常检测框架, 在离线部分该框架使用轨迹数据库挖掘不同路径的道路行为模型, 在线部分同时接收车辆GPS数据与社交平台数据, 当在线检测到的轨迹行为明显不同于行为模型时, 则判断此轨迹出现了异常行为, 并尝试用社交平台上的数据来解释这种异常.
本文考虑在套牌车检测方法中, 引入基于历史轨迹相似性的轨迹异常检测思想, 构建两阶段的套牌车检测框架, 离线阶段使用历史卡口监测数据构建路段速度阈值; 在线阶段通过持续观测多个时间窗口内具有异常行为的车辆, 将异常频度高的车辆判定为套牌车, 提升套牌车检测的准确率.
2 问题描述与算法框架在本节中, 我们将对套牌车检测框架做一个概述.在第2.1节中给出问题的定义, 第2.2节中介绍算法的整体框架.
2.1 问题描述城市道路的卡口摄像头数据即在城市道路, 高速公路出入口等地段的通过车辆自动识别系统采集到的过往车辆数据.通过卡口摄像头监测数据可以得到该卡口的ID、通过该卡口车辆的车牌号、车辆通过该卡口的时间戳等属性.令
套牌车检测框架如图 3所示, 包含离线和在线两个阶段.离线阶段, 通过城市卡口摄像头的监测数据可以获得各个车牌的轨迹.根据这些历史轨迹可以计算出各条路段分时段的速度分布, 得到速度阈值, 即认为当车辆经过该路段时, 其平均速度超过速度阈值则认为该段轨迹异常.在线阶段, 根据提取的各路段的速度阈值, 实时检测新采集的车牌轨迹中每一段子轨迹速度是否大于它通过路段的速度阈值, 若大于, 则认为该车牌出现异常, 将其加入套牌车候选集合持续观察.当套牌车候选集合中的车牌速度异常频度超过预设的阈值时, 则视为套牌车.为确保基于历史轨迹数据提取的各路段速度阈值的有效性, 将新采集到的轨迹数据同时用于路段速度分布的更新.
|
图 3 套牌车检测框架 Fig.3 Framework of fake plate vehicles detection |
针对上文所述, 分时段对各路段采用不同的速度阈值能有效提高套牌车检测的准确率.第3.1节介绍基于历史轨迹数据建立分时段的路段速度分布; 第3.2节介绍通过观测连续多个时间窗口下各路段车辆的行为, 以发现具有高频度异常的套牌车辆.
3.1 离线建立分时段的路段速度分布城市路网中的各路段都依照交通法规设定了相应的车速范围, 但实际中, 由于道路拥堵或其他道路异常事件, 车辆的实际行驶速度应低于规定的最高速度.若仅根据规定的路段最高速度来检测某一车辆是否异常, 会导致漏检从而造成检测准确率低下.根据历史卡口监测数据, 计算更为合理的速度阈值用于异常检测, 能够显著提高检测的准确率.
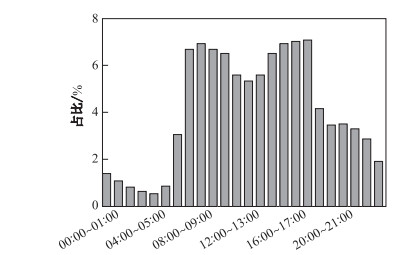
车辆的行驶速度与道路的地理位置有着较大的相关性, 如在城市的中心地带车辆的平均行驶速度明显低于郊区或高架等地带.因此在进行套牌检测时, 不同的路段应采用不同速度阈值.此外, 1 d中城市的道路状况往往随时间的推移而变化, 在上/下班等高峰时段, 由于车流量大, 车辆的行驶速度通常较闲暇时段慢.针对这种车流量分布不均匀的情况, 应将全天划分为多个时段, 使得同一时间段内的车辆行驶状况相似, 不同时间段内行驶状况差别显著.如图 4所示, 为某路段某天车流量随时间变化示例, 横轴表示时间, 纵轴是每个时段内车流量占全天车流量的百分比.通过观察可知, 白天的车流量较夜间的车流量高, 上下班高峰期的车流量占比最大.因此, 在此例中根据车流量的不同, 将全天划分为00:00~06:00、06:00~07:00、07:00~11:00、11:00~14:00、14:00~18:00、18:00~24:00等6个时段.
|
图 4 路段1 d车流量分布示例 Fig.4 Example of a traffic flow distribution |
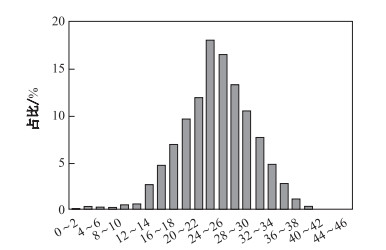
同一时段内, 经过同一路段车辆的速度也存在一定的变化, 例如部分车辆恰好遇到红灯, 则其行驶速度相对于畅通行驶的车辆会较低.如图 5所示, 描述了某路段中午11:00~12:00车速分布.横轴表示速度, 每2 km/h划分一个速度范围; 纵轴表示行驶速度在对应速度范围内的车辆占所有车辆的百分比.在中午11:00~12:00之间, 车辆经过该路段的速度集中在20~30 km/h, 只存在少量车辆速度偏离该范围较大.因此仅使用平均速度无法较好地描述此路段的实际情况; 而统计学上使用速度分布能更好地描述路段上车辆的行驶状况.由图 5可知, 车辆速度的分布呈现中间集中、两侧分散的特点.通过对多个路段数据的统计观察, 可知高斯分布能够较好地拟合同一路段上车辆行驶速度的状况.因此本文采用高斯分布对速度分布进行建模, 进而给出各路段分时段的正常速度阈值, 进行套牌车检测.
|
图 5 路段速度分布示例 Fig.5 Example of a road's speed distribution |
求解各路段分时段的速度分布, 即求解高斯分布中的参数:均值
| $ \begin{align*} p_{(r, t)} (v)=\frac{1}{\sqrt{2\pi } \sigma} \text{ e}^{-\frac{(v-\mu)}{2\sigma^2 }^2 }, \end{align*} $ |
其中
| $ \begin{align*} \widehat{\mu}=\, &\frac{1}{n}\sum\nolimits_{i=1}^nv_i, \\ \widehat{\sigma^2}=\, &\frac{1}{n}\sum\nolimits_{i=1}^n v_i^2 -\widehat{\mu}^2, \end{align*} $ |
其中,
车辆的轨迹是由卡口信息和对应时间戳组成的序列, 路段即指路网中相邻的卡口对.因此, 只需要计算相邻卡口之间的速度分布即可.针对每个分布, 根据历史数据, 计算在对应时间段经过该路段的所有车辆的平均速度, 进而计算
各路段的速度分布集合为
| $ \begin{align*} SDS=\{\langle \text{ID} _{s_1}, \text{ID}_{e_1 }, RDS_1 \rangle, \cdots, \langle \text{ID}_{s_p}, \text{ID}_{e_p}, RDS_p \rangle \} \end{align*} $ |
其中,
算法1描述了基于历史轨迹数据构建分时段路段速度分布的过程.
| 算法1 构建路段速度分布集合 |
|
输入: 轨迹集合 |
|
输出: 路段速度分布集合 |
| 1. |
| 2. |
| 3. |
| 4. |
| 5. continue; |
| 6. |
| 7. |
| 8. |
| 9. |
| 10. |
| 11. |
| 12. |
| 13. 初始化 |
| 14. |
| 15. |
| 16. 将 |
| 17. |
| 18. |
| 19. |
| 20. |
对每条历史轨迹, 遍历其所有连续的轨迹点.首先通过validate()函数判断这两个轨迹点的有效性(行4), 若两个轨迹点的时间间隔过长或车辆经过两个轨迹点之间的平均速度过大, 表明车辆可能中途停车或出现套牌现象, 则该车辆的速度并不能用于估计对应时段该路段的速度分布; 反之, 用其平均速度更新对应路段相应时间段的统计量.首先判断速度分布集合
通过估计的分时段的路段速度的分布, 能够计算各路段在不同时段的正常速度阈值.由高斯分布的性质可知
| $ \begin{align*} {\rm Threshold}=\widehat{\mu}+3 \widehat{\sigma}. \end{align*} $ |
例如某路段在某一时段, 其参数估计量为
结合城市各个卡口的监测数据可以构建车辆的轨迹序列, 通过车辆的轨迹计算出车辆在各个卡口间的平均速度, 并利用平均速度检测该车辆是否出现异常行为.车辆经过两个连续卡口的平均速度超过当前时段该路段的正常速度阈值, 则判定该车辆发生了一次异常行为, 因此将该车辆视为候选套牌车, 并放入套牌车候选集合E中.例如车牌为A3AP63的车辆经过卡口00006157与卡口00006230的时间间隔为56s(23: 03: 21和23: 04: 15), 两个卡口相距1.3 km, 根据第3.1节计算的路段速度阈值可知在晚上23: 00该路段的正常速度阈值为40 km/h, 而该车辆在此路段行驶的平均速度(86 km/h)远超该路段的速度阈值, 因此判断该车辆在此时出现一次异常行为.同一车牌车辆的轨迹可能存在多次异常行为.若仅根据车辆的一次异常行为就判定为套牌车, 极易造成误判情况的发生.因此只将其标记为异常, 加入套牌车候选集合
据观察, 若车辆被套牌, 即存在多辆车使用同一车牌在道路上违法行驶.因此, 套牌车的轨迹在一段时间内出现异常的频度远大于违法超速的车辆.利用滑动窗口模型持续观察实时采集的数据, 当同一个车牌的轨迹在连续
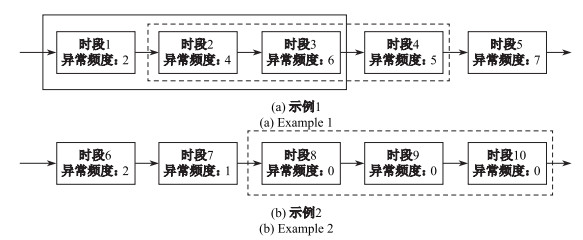
|
图 6 滑动窗口 Fig.6 Sliding window |
当检测到车辆产生1次异常行为时, 则将该车牌放入套牌车候选集合
| $ \begin{align*} E=\{\langle C_{e_1 }, C\text{List}_{e_1} \rangle, \langle C_{e_2 }, C\text{List}_{e_2} \rangle, \cdots, \langle C_{e_q }, C\text{List}_{e_q } \rangle \}, C_{e_i }\in L, 1\leq i\leq q, \end{align*} $ |
其中,
套牌车检测如算法2所示, 该算法用于在线检测连续时段内具有高频度异常的车辆, 并将其视为套牌车.
| 算法2 在线高频度异常车辆检测 |
|
输入: 一个时段摄像头数据集合 |
|
输出: 套牌车集合 |
| 1. 由 |
| 2. |
| 3. |
| 4. |
| 5. |
| 6. |
| 7. |
| 8. |
| 9. num=OutlierNum |
| 10. Update |
| 11. |
| 12. continue; |
| 13. |
| 14. |
| 15. |
| 16. |
| 17. |
| 18. 将 |
| 19. |
| 20. |
| 21. |
| 22. |
| 23. 将车牌 |
| 24. |
| 25. |
| 26. 将 |
| 27. |
给定一个时间段内的卡口摄像头检测数据集
本文套牌车检测算法对不同路段分时段采用不同的速度阈值以防止漏检, 同时使用滑动窗口模型持续监测异常车牌以避免误判的发生.新的数据除了用于套牌车的检测, 同时还用于增量更新路段速度分布模型, 这使得速度分布能不断调整以反映路段的真实的行驶情况.窗口长度
在本节中, 我们对套牌车检测框架进行了实验评估.所有算法均由Java语言实现且运行在处理器为Intel Core i5-4460 3.20 GHz、内存8 GB的Windows操作系统的PC机上.实验分为3部分:第一部分利用历史数据建立路段速度分布, 计算各路段分时段的正常速度阈值; 第二部分分析不同窗口长度
我们使用某市2014年9月1号到9月30号535个卡口摄像头监测数据, 每天产生的约530万条监测数据, 数据量约为7 GB, 记录了280万个不同的牌照.卡口摄像头采集数据主要包含卡口ID、车牌号、时间戳、车道号、卡口朝向、经纬度等16个属性.我们使用9月1日到9月20日的数据进行路段速度分布建模, 得到各路段分时段的正常速度阈值.对9月21日至9月30日的数据进行标注, 共标注5 000条轨迹, 其中人工标注获得104辆套牌车的954条轨迹.套牌车检测包含两个重要参数:滑动窗口大小
实验统计了16万个不同的路段, 将1 d分为6个时段, 约产生了96万个速度分布.对于每个速度分布, 我们不仅计算出其对应的正常速度阈值, 还计算对应时段内经过该路段所有车辆的平均速度.各路段分时段平均速度分布如图 7(a)所示, 横轴表示速度的区间, 纵轴表示速度在对应区间的占比, 如平均速度在10~20 km/h大约总体的41.7%.由图可知超过98%的路段的平均速度都在60 km/h以下, 且所有路段的平均速度均在80 km/h以下.卡口时间对比法设置统一的速度阈值如120 km/h来检测套牌车, 但不同时段各路段的平均速度不同且远小于120 km/h, 因此统一的速度阈值并不能有效地进行套牌车检测.各路段分时段的速度阈值分布如图 7(b)所示, 纵轴表示速度阈值在对应区间的占比, 其中各路段分时段的速度阈值主要集中在20~60 km/h, 速度阈值在80 km/h以下的超过90%, 仅存在极少的速度阈值超过100 km/h.对比两张图, 发现由各路段速度分布计算出的速度阈值明显大于平均速度, 但又远小于统一速度阈值(如120km/h).与平均速度相比, 各路段分时段的速度阈值比其平均速度快出29.1 km/h, 因此使用高斯分布对路段速度分布进行建模能够计算出更为合理的路段速度阈值.分时段的路段速度阈值能够有效地检测轨迹异常, 提高套牌车检测的准确性.
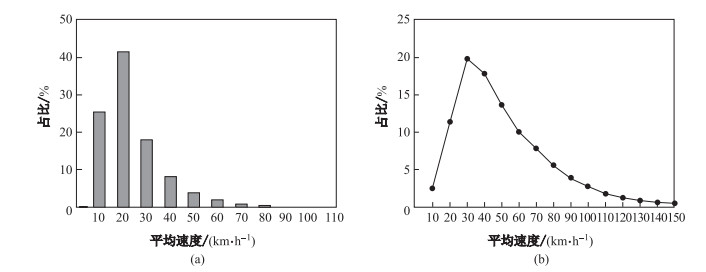
|
图 7 (a)、(b)各路段平均速度与速度阈值 Fig.7 (a)、(b)Average speed and threshold speed of every road |
套牌车检测实验中, 我们在不同窗口大小
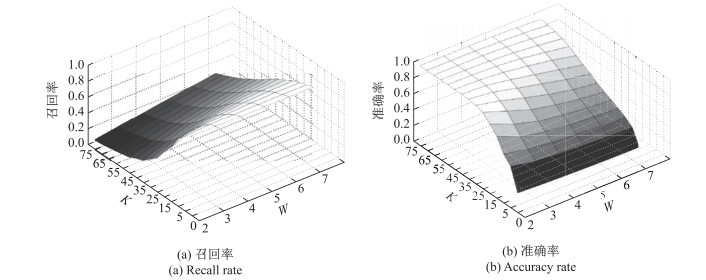
|
图 8 参数敏感性 Fig.8 Parameter effects |
图 9显示了参数
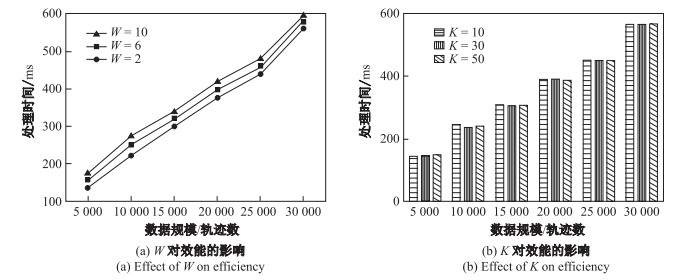
|
图 9 性能分析 Fig.9 Efficiency evaluation |
我们使用人工标注轨迹将本文检测框架与TP-Finder进行对比, 实验结果如图 10所示.图 10(a)中, 我们评估两个算法在不同的数据规模下的准确率.本文算法将窗口大小
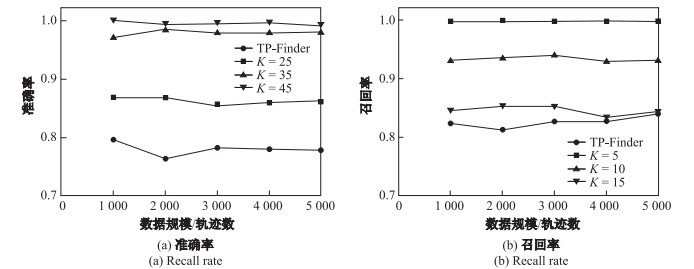
|
图 10 实验结果正确性对比 Fig.10 Comparisons of two method |
本文提出了一个两阶段的套牌车检测框架:离线阶段使用历史监测数据建立不同时段下路段的速度分布, 确定时空限制下的速度阈值; 在线阶段根据离线阶段构建的速度阈值, 基于滑动窗口模型连续观测多个时间窗口, 将具有频繁异常行为的车辆判定为套牌车.最后通过实验验证框架的有效性和实时性, 结果表明本框架能够有效避免噪声数据干扰, 实时进行套牌车的检测.在离线阶段, 对于时段的划分可以考虑使用MDL方法, 使划分结果更为合理.在处理海量数据时, 可使用Spark或Storm等分布式系统提升框架的处理性能.未来的工作主要包括套牌车轨迹的模式挖掘以及区分套牌车轨迹中的原车辆和套牌车.
| [1] | 唐晓东. 套牌机动车辆检测方法分析[J]. 中国人民公安大学学报(自然科学版), 2013, 19(2): 76-79. |
| [2] | 吴俊文, 范大伟. 一种汽车牌照防套牌装置: 中国, 200720000158. 4[P]. 2007-12-19. |
| [3] | 杨博. 物联网ZigBee技术在套牌车监管中的应用研究[J]. 制造业自动化, 2012, 34(17): 41-43. DOI:10.3969/j.issn.1009-0134.2012.9(s).14 |
| [4] | 李悦, 刘晨. 基于历史车牌识别数据的套牌车并行检测方法[J]. 计算机应用, 2016, 36(3): 864-870. DOI:10.11772/j.issn.1001-9081.2016.03.864 |
| [5] | 周傲英, 杨彬, 金澈清, 等. 基于位置的服务:架构与进展[J]. 计算机学报, 2011, 34(7): 1155-1171. |
| [6] | LIU H P, JIN C Q, ZHOU A Y. Popular route planning with travel cost estimation[C]//Proceedings, Part Ⅱ, of the 21st International Conference on Database Systems for Advanced Applications-Volume 9643. New York: Springer-Verlag Inc, 2016: 403-418. |
| [7] | WU C H, HO J M, LEE D T. Travel-time prediction with support vector regression[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4): 276-281. DOI:10.1109/TITS.2004.837813 |
| [8] | CHEN Z B, SHEN H T, ZHOU X F. Discovering popular routes from trajectories[C]//2011 IEEE 27th International Conference on Data Engineering (ICDE). 2011: 900-911. |
| [9] | DENG C Y, XUE L F, LI W Q, et al. The real-time monitoring system for inspecting car based on RFID, GPS and GIS[C]//2010 International Conference on Environmental Science and Information Application Technology. IEEE, 2010: 772-775. |
| [10] | IQBAL U, ZAMIR S W, SHAHID M H, et al. Image based vehicle type identification[C]//2010 International Conference on Information and Emerging Technologies. IEEE, 2010, Page(s): 1-5. DOI: 10.1109/ICIET.2010.5625675. |
| [11] | 卢晓春, 周欣, 蒋欣荣, 等. 基于网格化监控的套牌车检测系统[J]. 计算机应用, 2009, 29(10): 2847-2848. |
| [12] | 毛嘉莉, 金澈清, 章志刚, 等. 轨迹大数据异常检测:研究进展及系统框架[J]. 软件学报, 2017, 28(1): 17-34. |
| [13] | LEI P R. A framework for anomaly detection in maritime trajectory behavior[J]. Knowledge and Information Systems, 2016, 47(1): 189-214. DOI:10.1007/s10115-015-0845-4 |
| [14] | ZHU J, JIANG W, LIU A, et al. Time-dependent popular routes based trajectory outlier detection[C]//International Conference on Web Information Systems Engineering-WISE 2015. Berlin: Springer International Publishing, 2015: 16-30. |
| [15] | PAN B, ZHENG Y U, WILKIE D, et al. Crowd sensing of traffic anomalies based on human mobility and social media[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. 2013: 344-353. |




