在粒子物理领域, 研究强子问题的基本理论是量子色动力学(Quantum Chromodynamics, QCD)[1-3].但对于低能强子, 由于非微扰效应导致无法直接使用QCD理论进行解析计算[4]. 20世纪70年代, 一些物理学家发现有效场理论(Effective Field Theory, EFT)可以描述QCD的低能结构.在低能区, QCD可表述为基于手征对称性自发破缺的Goldstone玻色子(即
但在涉及重子的中低能动力学过程中, 由于重子质量以额外能标出现, 会造成重子质量项破坏手征幂次规则的行为.为解决这个问题, 有人提出了重重子手征微扰论(Heavy Baryon ChPT, HBChPT)[11-13]. HBChPT把重子的质量项从重子传播子中约掉(低能或静态近似), 由此避免了额外能标的出现, 保证了正确的幂次规则.但这个近似只能在远低于重子质量(某些过程的阈值)的范围内取得较为满意的结果, 而在计算某些能标靠近重子质量(或阈值)的过程或物理量时, 得出的解析结果往往不够完整, 或不正确[14].因此在涉及重子的中低能过程中, 手征微扰论的应用会出现这样的困难:采用相对论性的协变手征微扰论计算时, 在圈图计算结果中会出现不遵守手征幂次规则的贡献; 而采用更为简单的HBChPT计算, 虽然满足手征幂次规则, 但可能会得到错误的重子阈值结构及其他问题.目前学术界倾向于引入各种正规化方案来克服这些困难[15-16].
基于手征微扰论的这一困难, 本小组一直在为建立一个较满意的低能QCD有效场论框架做尝试与探讨, 我们已经采用相对论性的协变微扰论方法研究了核子-核子散射等核力问题, 也取得了一定的成果[10, 14, 17], 现在将其拓展到强子结构的研究领域.由于强子结构函数以及部分子分布函数可以有效地揭示强子内部结构的各种信息, 它们可通过Twist-2算符的矩阵元来定义[18], 因此计算Twist-2算符的矩阵元有着重要的理论意义.现有的理论计算大部分采用重重子手征微扰论[19-21], 为了保证解析结果的正确性, 本文将采用协变手征微扰理论计算分析Twist-2算符在单核子态下的矩阵元, 并与重重子理论的计算作比较, 从而为中低能核子或重子结构的研究做出新的探索.
本文主要内容为:第1节给出基本理论框架下的拉格朗日量和Twist-2算符; 第2节进行具体的费曼图计算与分析; 第3节是结论与展望.
1 基本框架本文采用的协变手征微扰理论中
| $ \begin{align} L=\dfrac{f_\pi ^2 }{4}{\rm tr}\Big[{\partial _\mu \Sigma \partial ^\mu \Sigma ^++m_\pi ^2 ( {\Sigma +\Sigma ^+} )} \Big]+\overline \Psi \Big[{i\gamma ^\mu D_\mu-M_{\rm N} +\dfrac{g_{\rm A}}{2}\gamma ^\mu \gamma ^5u_\mu }\Big]\Psi, \end{align} $ | (1) |
其中,
| $ \begin{align} {\Sigma }=\exp\Big( \dfrac{{\rm{i}}\overrightarrow{\tau }\cdot\overrightarrow{\pi}}{f_{\pi}}\Big), \end{align} $ | (2) |
| $ \begin{align} D_\mu &\equiv \partial _\mu +\varGamma _\mu, \end{align} $ | (3a) |
| $ \begin{align} u_\mu &\equiv {\rm{i}}\{ {\xi ^+, \partial _\mu \xi } \}, \end{align} $ | (3b) |
| $ \begin{align} \varGamma _\mu &\equiv \dfrac{1}{2}\Big[{\xi ^+, \partial _\mu \xi }\Big], \end{align} $ | (3c) |
| $ \begin{align} {\xi }&\equiv \sqrt{\Sigma }. \end{align} $ | (3d) |
式(1)中的拉氏量给出协变框架下的顶角和传播子, 具体的费曼规则可参阅文献[24].
本文的主要工作是通过计算Twist-2算符在核子态下的矩阵元, 从而间接研究强子的结构, 因此需要构造此算符.理论上我们应该构造相对论协变框架下的Twist-2算符, 但由于现有的大部分文献都是采用重重子理论下构造出的比较简单的算符形式, 而且我们也想要尽快验证我们的想法, 加之篇幅的限制, 本文先进行拟相对论的计算, 即采用重重子框架下的Twist-2算符[21]和相对论协变形式的顶角与传播子, 这样基本可以避免错误阈值结构的问题.由于协变框架下的Twist-2算符的构造与计算更加复杂, 我们将在另文处理.重重子理论下构造的Twist-2算符为
| $ \begin{align} &\widehat{O}_{\pi, \mu _1 \cdots \mu _n }^{(n), a} \!=\!a^{(n)}({\rm{i}} )^n\dfrac{f_\pi ^2 }{2}\Big( {\dfrac{1}{{\Lambda }_x }} \Big)^{n\!-\!1}{\rm tr}[{{\Sigma }^+\tau ^a\overrightarrow{\partial}_{\mu_1}\cdots\overrightarrow{\partial }_{\mu_n}\Sigma\!+\!\Sigma\tau^a} \overrightarrow{\partial}_{\mu _1 }\cdots \overrightarrow{\partial}_{\mu_n}\Sigma^+]-{\rm traces}, \end{align} $ | (4a) |
| $ \begin{align} &\widehat{O}_{{\rm N}, \mu _1 \cdots \mu _n }^{(n), a} =A^{(n)}v_{\mu _1 } v_{\mu _2 } \cdots v_{\mu _n } \overline{\Psi }\tau _{\xi +}^a \Psi -{\rm traces}, \end{align} $ | (4b) |
其中,
| $ \begin{align} \tau _{\xi +}^a \equiv \dfrac{1}{2}({\xi \tau ^a\xi ^+ +\xi ^+\tau ^a\xi }), \end{align} $ | (5) |
本文主要关心Twist-2算符在单核子态下的矩阵元, 其一圈图水平的贡献见图 1所列费曼图.
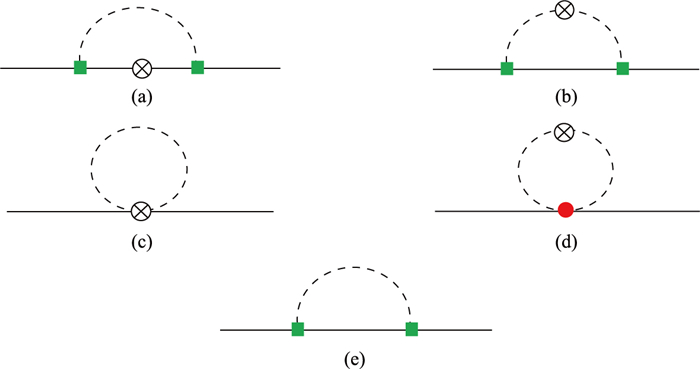
|
图 1 单核子态下的一圈图 Fig.1 One-loop diagrams for single-nucleon states |
图 1中的实线表示相对论性核子线, 虚线表示
由于
| $ \begin{align} \varGamma _{{\rm tree}}^{(1)}=A^{(1)}v_{\mu _1 } \bar {u}_p \tau ^au_p. \end{align} $ | (6) |
由费曼规则可得图 1(a)的费曼振幅为
| $ \begin{align} \varGamma _a^{(1)} =-{\rm{i}}\dfrac{g_{\rm A}^2 }{4f_\pi ^2 }A^{(1)} v_{\mu _1 } \overline{u}_p\tau^a\int {} \dfrac{{\rm{d}}^4l}{(2\pi)^4} \cdot\dfrac{l\!\!/\gamma_5(p\!\!/-l\!\!/+M_{\rm N})(p\!\!/-l\!\!/+M_{\rm N}) l\!\!/\gamma_5}{A_{\pi}A^2_{\rm N}}u_p, \end{align} $ | (7) |
其中
| $ \begin{align} &A_\pi =l^2-m_\pi ^2 +{\rm{i}}\varepsilon, \end{align} $ | (8a) |
| $ \begin{align} &A_{\rm N} =({p-l} )^2-M_{\rm N}^2 +{\rm{i}}\varepsilon. \end{align} $ | (8b) |
这里
| $ \begin{align} & {p\!\!/}u_p =M_{\rm N} u_p, \end{align} $ | (9a) |
| $ \begin{align}& p_\mu =M_{\rm N} v_\mu, \end{align} $ | (9b) |
| $ \begin{align}& p^2=M_{\rm N}^2. \end{align} $ | (9c) |
分子可化简为
| $ \begin{align} \overline{u}_p\tau^al\!\!/\gamma_5(p\!\!/-l\!\!/+M_{\rm N})(p\!\!/-l\!\!/+M_{\rm N})l\!\!/\gamma_5u_p= \overline{u}_p(-A^2_{\rm N}-4M_{\rm N}A_{\rm N}l\!\!/-4M^2_{\rm N}l^2)\tau^au_p. \end{align} $ | (10) |
最后得到的协变解析结果是
| $ \begin{align} \varGamma _a^{(1)} =&\varGamma _{{\rm tree}}^{(1)} \dfrac{g_{\rm A}^2 }{64\pi ^2f_\pi ^2 }\Big(M_{\rm N}^2 \Big( {\!-\!6\varGamma ( \varepsilon )\!-\!2\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }\!-\!4\ln \dfrac{4\pi \mu ^2}{M_{\rm N}^2 }\!+\!4\ln \rho \!-\!2}\Big)\notag \\ &\!+\!m_\pi ^2 \Big( {\!-\!\varGamma ( \varepsilon )\!-\!\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }\!+\!8\ln \rho \!-\!3} \Big) \! +\!\Big( {\dfrac{2m_\pi ^5 }{M_{\rm N}^3 }\!+\!\dfrac{6m_\pi ^3 }{M_{\rm N} }} \Big)\arctan \sqrt {4\rho ^2-1} \!-\!\dfrac{2m_\pi ^4 }{M_{\rm N}^2 }\ln \rho \Big), \end{align} $ |
其中
现在分解
| $ \begin{align} 2\ln( \rho )=\Big\langle {\varGamma (\varepsilon )+\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }}\Big\rangle -\Big\langle {\varGamma ( \varepsilon )+\ln \dfrac{4\pi \mu ^2}{M_{\rm N}^2 }} \Big\rangle, \end{align} $ | (12) |
这样
| $ \begin{align} \varGamma _a^{( 1 )}=&\varGamma _{{\rm tree}}^{(1)} \dfrac{g_{\rm A}^2 }{64\pi ^2f_\pi ^2 }\Big( \Big\langle {M_{\rm N}^2\Big( {-6\varGamma ( \varepsilon)-6\ln \dfrac{4\pi \mu ^2}{M_{\rm N}^2 }-2} \Big) +m_\pi ^2 \Big( {-4\varGamma ( \varepsilon )-4\ln \dfrac{4\pi \mu ^2}{M_{\rm N}^2 }} \Big)} \Big\rangle \notag\\ & \!+\!\Big[{m_\pi ^2 ( {3\varGamma ( \varepsilon )\!+\!3\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }\!-\!3})} \Big] \!+\!\Big\{ {\Big( {\dfrac{2m_\pi ^5 }{M_{\rm N}^3 }\!+\! \dfrac{6m_\pi ^3 }{M_{\rm N} }} \Big)\arctan \sqrt {4\rho ^2\!-\!1}\! -\!\dfrac{2m_\pi ^4 } {M_{\rm N}^2 }\ln \rho } \Big\} \Big). \end{align} $ | (13) |
显然图 1(a)对矩阵元的贡献可以分解为3类:尖括号里是来自大的圈动量区域的贡献(依赖于核子质量), 这些贡献显然破坏手征幂次规则, 但都是定域项, 因此可以自然地通过引入定域抵消项来减除; 中括号里的项是完全遵守手征幂次规则的定域项; 大括号里是更小的高阶相对论效应, 在重重子理论下, 这部分贡献与满足手征幂次规则的项相比很小而被舍去, 本文也做如此处理.所以在此结果中减掉大的破坏手征幂次规则的定域项和满足手征幂次规则的发散, 并忽略高阶相对论效应, 得到图 1(a)中满足手征幂次规则的主要有限贡献是
| $ \begin{align} \varGamma _a^{(1)} =\varGamma _{{\rm tree}}^{(1)} \Big( {\dfrac{3g_{\rm A}^2 }{64\pi ^2f_\pi ^2 } m_\pi ^2 \ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }} \Big). \end{align} $ | (14) |
图 1(b)的费曼振幅为
| $ \begin{align} \varGamma _b^{(1)} =i\dfrac{2g_{\rm A}^2 }{f_\pi ^2 }a^{(1)}\overline{u}\tau^a\int {} \dfrac{{\rm{d}}^4l}{(2\pi )^4}\cdot\dfrac{l_{\mu_1}l\!\!/\gamma_5(p\!\!/-l\!\!/+M_{\rm N})l\!\!/ \gamma_5} {A^2_{\pi}A_{\rm N}}u_p. \end{align} $ | (15) |
积分结果为
| $ \begin{align} {\varGamma }_b^{(1)} =&\varGamma _{{\rm tree}}^{(1)} \dfrac{g_{\rm A}^2 }{16\pi ^2f_\pi ^2 }\Big( M_{\rm N}^2\Big( {2{\varGamma }( \varepsilon )+2\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }-4\ln \rho +2} \Big) \notag\\ &\!+\!m_\pi ^2 \Big( {{\varGamma }( \varepsilon )\!+\!\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }\!-\!8\ln \rho \!+\!7} \Big) \!+\!\Big( {\dfrac{2m_\pi ^5 }{M_{\rm N}^3 }-\dfrac{10m_\pi ^3 }{M_{\rm N} }} \Big) \arctan \sqrt {4\rho ^2\!-\!1} \!+\!\dfrac{6m_\pi ^4 }{M_{\rm N}^2 }\ln \rho \Big). \end{align} $ | (16) |
同样可以分解为
| $ \begin{align} {\varGamma }_b^{(1)} =&\varGamma _{{\rm tree}}^{(1)} \dfrac{g_{\rm A}^2 }{16\pi ^2f_\pi ^2 }\Big( \Big\langle {M_{\rm N}^2 \Big({2{\varGamma }( \varepsilon)+2\ln \dfrac{4\pi \mu ^2}{M_{\rm N}^2 }+2}\Big)+m_\pi ^2 \Big({{4\varGamma }( \varepsilon )+4\ln \dfrac{4\pi \mu ^2}{M_{\rm N}^2 }}\Big)}\Big\rangle \notag\\ & +\!\Big[{m_\pi ^2\Big( {\!-\!3{\varGamma }( \varepsilon )\!-\!3\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }\!+\!7} \Big)}\Big] \!+\!\Big\{ {\Big( {\dfrac{2m_\pi ^5 }{M_{\rm N}^3 }\!-\!\dfrac{10m_\pi ^3 }{M_{\rm N} }} \Big)\arctan \sqrt {4\rho ^2\!-\!1} \!+\!\dfrac{6m_\pi ^4 }{M_{\rm N}^2 }{\ln }\rho } \Big\} \Big). \end{align} $ | (17) |
可见, 与图 1(a)一样, 图 1(b)的贡献可分解为3类:破坏幂次规则的大定域项、满足手征幂次规则的项和高阶相对论效应.采用如图 1(a)的减除方法, 最后得到图 1(b)中满足手征幂次规则的主要贡献为
| $ \begin{align} {\varGamma }_b^{(1)} =\varGamma _{{\rm tree}}^{(1)}\Big( {\dfrac{-3g_{\rm A}^2 }{16\pi ^2f_\pi ^2 }m_\pi ^2 \ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }} \Big). \end{align} $ | (18) |
图 1(c)的费曼振幅为
| $ \begin{align} \varGamma _c^{(1 )} =-{\rm{i}}\dfrac{1}{f_\pi ^2 }A^{( 1)}\overline{u}_p\tau^a\int {} \dfrac{{\rm{d}}^4l}{(2\pi)^4}\cdot\dfrac{ \gamma_{\mu_1}}{l^2-m^2_\pi+{\rm{i}}\varepsilon}u_p. \end{align} $ | (19) |
此图完全来自于Twist-2算符自缩并的贡献, 结构比较简单, 经计算得到的结果是
| $ \begin{align} \varGamma _c^{(1)} =\varGamma _{{\rm tree}}^{(1)} \dfrac{m_\pi ^2 }{16\pi ^2f_\pi ^2 }\Big( {{\varGamma }( \varepsilon)+\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }+1}\Big). \end{align} $ | (20) |
结果完全满足手征幂次规则.
同理可得
| $ \begin{align} \varGamma _d^{( 1 )} =-\varGamma _{{\rm tree}}^{(1)} \dfrac{m_\pi ^2 }{16\pi ^2f_\pi ^2 }\Big({{\varGamma }( \varepsilon )+\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }+1}\Big). \end{align} $ | (21) |
图 1(d)的贡献也满足手征幂次规则, 且与图 1(c)结果相反, 即
图 1(e)是用于核子外线重整化的核子自能图, 文献[25]中已经给出.我们需要的核子外线抵消项为
| $ \begin{align} \delta Z_{\rm N} =&\dfrac{3g_{\rm A}^2 }{64\pi ^2f_\pi ^2 }\Big( \Big\langle {2m_\pi ^2 ( {-\varGamma ( \varepsilon )-\ln \dfrac{4\pi \mu ^2}{M_{\rm N}^2 }} \Big)} \Big\rangle +\Big[{m_\pi ^2 \Big( {3\varGamma ( \varepsilon)+3\ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }-3}\Big)}\Big] \notag\\ & +\Big\{ {\Big( {-\dfrac{2m_\pi ^5 }{M_{\rm N}^3 }+\dfrac{6m_\pi ^3 }{M_{\rm N} }} \Big)\arctan \sqrt {4\rho ^2-1} -\dfrac{4m_\pi ^4 }{M_{\rm N}^2 }\ln \rho }\Big\}\Big). \end{align} $ | (22) |
该图对矩阵元的有限贡献为
| $ \begin{align} \varGamma _e^{(1)} =\varGamma _{{\rm tree}}^{(1)}\Big( {\dfrac{9g_{\rm A}^2 }{64\pi ^2f_\pi ^2 }m_\pi ^2 \ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }} \Big). \end{align} $ | (23) |
上面所有图的总结果及讨论安排在第2.3节.
2.2| $ \begin{align} \varGamma _{{\rm tree}}^{(n )} =A^{(n)}v_{\mu _1 } \cdots v_{\mu _n } \overline{u}_p\tau^au_p, \end{align} $ | (24) |
这里的
图 1(a)的费曼振幅为
| $ \begin{align} \varGamma _a^{( n )} =-{\rm{i}}\dfrac{g_{\rm A}^2 }{4f_\pi ^2 }A^{(n)}v_{\mu _1 } v_{\mu _2 } \cdots v_{\mu _n } \overline{u}_p\tau^a\int {} \dfrac{{\rm{d}}^4l}{(2\pi)^4}\cdot\dfrac{l\!\!/\gamma_5(p\!\!/-l\!\!/+M_{\rm N})(p\!\!/-l\!\!/+M_{\rm N})l\!\!/\gamma_5}{A_\pi A^2_N}u_p. \end{align} $ | (25) |
与
| $ \begin{align} \varGamma _a^{(n)} =\varGamma _{{\rm tree}}^{(n)}\Big( {\dfrac{3g_{\rm A}^2 }{64\pi ^2f_\pi ^2 }m_\pi ^2 \ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }} \Big). \end{align} $ | (26) |
图 1(c)的情况与图 1(a)类似; 对于图 1(e), 其提供的核子外线重整化因子与
| $ \begin{align} \varGamma _c^{(n)} =\varGamma _{{\rm tree}}^{(n)}\Big( {\dfrac{1}{16\pi ^2f_\pi ^2 }m_\pi ^2 \ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }}\Big), \end{align} $ | (27) |
| $ \begin{align} \varGamma _e^{(n)}=\varGamma _{{\rm tree}}^{(n)} \Big( {\dfrac{9g_{\rm A}^2 }{64\pi ^2f_\pi ^2 }m_\pi ^2 \ln \dfrac{4\pi \mu ^2}{m_\pi ^2 }} \Big). \end{align} $ | (28) |
由此可知图 1(a)、图 1(c)、图 1(e)的圈修正结构没有改变, 但图 1(b)和图 1(d)的贡献与
| $ \begin{align} &{\varGamma }_b^{(n)} ={\rm{i}}\dfrac{2g_{\rm A}^2 }{f_\pi ^2 }a^{(n)}\Big( {\dfrac{1}{\Lambda _x }} \Big)^{n-1}\overline{u}_p\tau^a\int {} \dfrac{{\rm{d}}^4l}{(2\pi)^4}\cdot \dfrac{(l_{\mu_1}\cdots l_{\mu_n})l\!\!/\gamma_5(p\!\!/-l\!\!/+M_{\rm N})l\!\!/\gamma_5}{A^2_\pi A_{\rm N}}u_p, \end{align} $ | (29) |
| $ \begin{align} &\varGamma _d^{(n)} =2{\rm{i}}a^{(n)}\Big( {\dfrac{1}{{\Lambda }_x }} \Big)^{n-1}\dfrac{1}{f_\pi ^2 }\overline{u}_p\tau^a\int {} \dfrac{{\rm{d}}^4l}{(2\pi )^4}\cdot\dfrac{l\!\!/l_{\mu_1}\cdots l_{\mu_n}}{A^2_\pi}u_p. \end{align} $ | (30) |
由于因子
综合树图与所有圈图的领头阶手征性贡献, 在
| $ \begin{align} M^{( 1)}=\varGamma _{{\rm tree}}^{(1)} +{\varGamma }_a^{(1)} +{\varGamma }_b^{( 1 )} +{\varGamma }_c^{(1)} {+\varGamma }_d^{(1)} +\varGamma _e^{(1)} =\varGamma _{{\rm tree}}^{(1)}. \end{align} $ | (31) |
原因很简单:在
在
| $ \begin{align} M^{(n)}&=\varGamma _{{\rm tree}}^{(n)} +{\varGamma }_a^{(n)} +{\varGamma }_c^{(n)} +{\varGamma }_e^{(n)} +\delta Z_O \varGamma _{{\rm tree}}^{(n)} \notag\\ &=\varGamma _{{\rm tree}}^{(n)} \Big( {1-\dfrac{3g_{\rm A}^2 +1}{16\pi ^2f_\pi ^2 }m_\pi ^2 \ln \dfrac{m_\pi ^2 }{4\pi \mu ^2}}\Big), \end{align} $ | (32) |
其中
以上的结果与文献[21]在重重子手征微扰论下的计算结果完全一致.综合
| $ \begin{align} M=\varGamma _{{\rm tree}}^{(n)}\Big({1-({3g_{\rm A}^2 +1})\dfrac{1-\delta ^{n1}}{16\pi ^2f_\pi ^2 }m_\pi ^2 \ln \dfrac{m_\pi ^2 }{4\pi \mu ^2}} \Big). \end{align} $ | (33) |
本文采用协变手征微扰论计算分析了一圈图水平上Twist-2算符在单核子态下的矩阵元, 并对得到的解析结果进行了分解处理, 在取核子质量很大时, 回到了重重子手征微扰论的计算结果.由计算可知, 在协变手征有效理论中, 破坏手征幂次规则的项完全是定域的, 可以通过定域抵消项来减除, 余下的正是满足手征幂次规则的贡献.因此采用协变形式的手征微扰论来计算重子的部分子分布函数等强子结构问题时, 可以做到既不丢失正确的解析行为, 又能得到满足手征幂次规则的贡献, 很好地克服了重重子理论中可能出现的错误阈值结构的问题, 更适合作为研究强子物理的有效场理论框架.
虽然本文采用的是重重子理论下构造的Twist-2算符, 但与完全相对论形式的计算(主要计算工作已完成, 目前在整理撰写阶段)相比, 解析结果的主要结构一致, 差异表现在大定域项(含发散)以及可略的高阶相对论效应, 不影响我们对主要问题的分析以及所得到的结论.将来我们期望将此方法应用到此矩阵元的高圈图修正或其他物理过程的研究计算中, 力争为构建一个满意的手征有效理论应用框架做出有益的贡献.
| [1] | CHENG T P, LI L F. Gauge Theory of Elementary Particle Physics[M]. New York: Oxford University Press Inc, 1984. |
| [2] | DONOGHUE J F, GOLOWICH E, HOLSTEIN B R, et al. Dynamics of the standard model[J]. Physics Today, 1994, 47: 91 |
| [3] | NOWAK M A, RHO M, ZAHED I. Chiral Nuclear Dynamics[M]. [S. l. ]: World Scientific Publishing Co Pte Ltd, 1992. |
| [4] | PAGELS H. Departures from chiral symmetry[J]. Physics Reports, 1975, 16(5): 219-311. DOI:10.1016/0370-1573(75)90039-3 |
| [5] | GASSER J, LEUTWYLER H. Chiral perturbation theory:expansions in the mass of the strange quark[J]. Nuclear Physics B, 1985, 250(1-4): 465-516. DOI:10.1016/0550-3213(85)90492-4 |
| [6] | WEINBERG S. Phenomenological lagrangians[J]. Physica A:Statistical Mechanics and its Applications, 1979, 96(1-2): 327-340. DOI:10.1016/0378-4371(79)90223-1 |
| [7] | WEINBERG S. Nuclear forces from chiral Lagrangians[J]. Physics Letters B, 1990, 251(2): 288-292. DOI:10.1016/0370-2693(90)90938-3 |
| [8] | BEDAQUE P F, VAN KOLCK U. Effective field theory for few-nucleon systems[J]. Annual Review of Nuclear and Particle Science, 2002, 52(1): 339-396. DOI:10.1146/annurev.nucl.52.050102.090637 |
| [9] | YANG J F. A note on nonperturbative renormalization of effective field theory[J]. Journal of Physics A:Mathematical and Theoretical, 2009, 42(34): 345402 DOI:10.1088/1751-8113/42/34/345402 |
| [10] | YANG J F. Nonperturbative NN scattering in 3S1-3D1 channels of EFT(π)[J]. Annals of Physics, 2013, 339: 160-180. DOI:10.1016/j.aop.2013.08.017 |
| [11] | JENKINS E, MANOHAR A V. Baryon chiral perturbation theory using a heavy fermion lagrangian[J]. Physics Letters B, 1991, 255(4): 558-562. DOI:10.1016/0370-2693(91)90266-S |
| [12] | BERNARD V, KAISER N, KAMBOR J, et al. Chiral structure of the nucleon[J]. Nuclear Physics B, 1992, 388(2): 315-345. DOI:10.1016/0550-3213(92)90615-I |
| [13] | PARK T S, MIN D P, RHO M. Chiral dynamics and heavy-fermion formalism in nuclei:Exchange axial currents[J]. Physics Reports, 1993, 233(6): 341-395. DOI:10.1016/0370-1573(93)90099-Y |
| [14] | 李帆. 核子与核子散射的手征有效场论分析[D]. 上海: 华东师范大学, 2015. |
| [15] | BECHER T, LEUTWYLER H. Baryon chiral perturbation theory in manifestly Lorentz invariant form[J]. The European Physical Journal C, 1999, 9(4): 643-671. DOI:10.1007/s100530050518 |
| [16] | GEGELIA J, JAPARIDZE G. Matching the heavy particle approach to relativistic theory[J]. Physical Review D, 1999, 60(11): 1615-1620. |
| [17] | YANG J F. Anomalous "mapping" between pionfull and pionless EFT's[J]. Modern Physics Letters A, 2014, 29(09): 1450043 DOI:10.1142/S0217732314500436 |
| [18] | BELITSKY A V, RADYUSHKIN A V. Unraveling hadron structure with generalized parton distributions[J]. Physics Reports, 2005, 418(1): 1-387. |
| [19] | DIEHL M, MANASHOV A, SCHÄFER A. Chiral perturbation theory for nucleon generalized parton distributions[J]. The European Physical Journal A, 2006, 29(3): 315-326. DOI:10.1140/epja/i2006-10098-4 |
| [20] | DIEHL M, Manashov A, SCHÄFER A. Generalized parton distributions for the nucleon in chiral perturbation theory[J]. The European Physical Journal A, 2007, 31(3): 335-355. DOI:10.1140/epja/i2007-10002-x |
| [21] | ARNDT D, SAVAGE M J. Chiral corrections to matrix elements of twist-2 operators[J]. Nuclear Physics A, 2002, 697(1-2): 429-439. DOI:10.1016/S0375-9474(01)01223-4 |
| [22] | CALLAN JR C G, COLEMAN S R, WESS J, et al. Structure of phenomenological Lagrangians. Ⅱ[J]. Physical Review, 1969, 177(5): 2247-2250. DOI:10.1103/PhysRev.177.2247 |
| [23] | GASSER J, SAINIO M E, ŠVARC A. Nucleons with chiral loops[J]. Nuclear Physics B, 1988, 307(4): 779-853. DOI:10.1016/0550-3213(88)90108-3 |
| [24] | MACHLEIDT R, ENTEM D R. Chiral effective field theory and nuclear forces[J]. Physics Reports, 2011, 503(1): 1-75. DOI:10.1016/j.physrep.2011.02.001 |
| [25] | SCHERER S, SCHINDLER M R. A Primer for Chiral Perturbation Theory[M]. Berlin: Springer Science & Business Media, 2011. |




