0 引言

随着信息技术的高速发展, 传统的法学研究方法和法律应用模式早已难以应对日新月异的社会需求与时代步伐.就国内外的研究现状而言, 将数据科学、智能算法等数理思想融入社会科学的研究与实践之中, 从而对人文社科领域进行交叉性研究的不多.近年来, 人工智能技术和大数据技术逐渐渗透到其他领域, "智能+"与"数据驱动"的研究模式已经在诸多领域进行应用.但由于法律的先天抽象属性, 以及法学研究对数据与计算科学的本能性排斥, 致使此类研究难及法律领域.而在一般哲学的视角下, 一门科学只有当引入数学或数据形成运算时, 才可实现学科的发展, 这也是为何法律行业发展远不及经济学等带有数理属性行业的缘由.纵然国内已然存在"计算法学"、"计量法学"等交叉研究概念, 但仍未真正意义上地实现对法律关系的数据化运算, 产业界也未存在以机器学习和大数据为驱动的法律"强人工智能".因此, 本文将聚焦新的法计算学理论, 以此为线索, 将"智能+数据"的驱动模式应用于律师辅助决策, 提出数据样本集的构建以及辅助决策的具体算法.

本文主要以交叉学科研究作为连接理论与技术的纽带, 不仅为计算科学领域内的研究者提供法律场景下的算法实现思路, 也对法学等社会科学研究具有进步性意义.主要贡献如下:

(1) 提出了不同于计算法学的法计算学的概念, 并明确其作为对法律科学进行数据化研究的理论, 其核心应当是实现法律关系的可计算化;

(2) 以"涵摄分类"建立了法律关系与数据分类算法之间的联系, 求得将法律进行数据化转化的连结点, 以C4.5决策树原理实现了对案件事实的法律定性分类;

(3) 构建了法律关系坐标系, 实现了将低维的法律关系分析向立体空间几何的转化;

(4) 实现了辅助律师进行案件分析决策的算法, 以多次朴素贝叶斯原理预测的概率之差作为优化案由的参考性路径, 且经与真实律师的代理思路与结果的比较, 验证了算法的可行性与准确性.

1 法计算学理论的引入 1.1 法律科学的量化研究现状

在世界范围内, 对法律与法学进行数据化与量化的研究发轫于"计量法学". "计量法学"的概念由Lee Loevinger提出, 其主张将量化思维融入到法学分析中, 强调运用电子计算机和符号逻辑来解决法律问题^[1].而我国国内对法律或法学的定量研究则基本以法学领域内的专家为主^[2], 很少有计算机技术和数据科学技术的人员参与其中^[3].故而我国早期的计量法学仅停留在对法律数据的单纯统计或计算, 而未形成一种科学的理论构架, 对法律的"计算"的本质缺乏正确的认识.伴随着国内人工智能热潮的兴起, 张妮、蒲亦非等逐渐发现先前"计量法学"的不足, 而将其重新定位至"计算法学"的领域, 从而采用统计学、现代数学、人工智能等技术方法对与法律相关的数据进行研究^[4].

但由于计算法学的研究对计算机技术和研究成本的要求较高, 已开展的研究与应用较少.目前较为成熟的法律智能系统均集中于欧美国家.如英国开发的法律一案征询公众意见系统Parmendies^[5]、法国引入的基于优先算法的电子投票程序^[6], 以及美国的刑事案件法律机器人智能审理^[7]等.而我国国内的法律智能化应用均集中于刑事司法活动^[8], 流程化、单一化的色彩较为浓重, 也难以涵盖现实生活中纷繁复杂的民事及经济等实体法律关系.由此可见, 目前各类法律量化研究存在以下明显不足: ①对法律的量化研究仅有法学学者开展, 缺乏计算机技术支撑, 难以呈现先进的研究成果; ②学界研究仅停留在理论形成阶段, 以抽象的概括性研究为主, 未涉及到计算科学的具体应用; ③当前研究以"解决问题式"的应对型思维为主, 尚停留在个案分析、判决书文本分析阶段, 缺乏对体系性共识和方法论的构建.因此, 以上困境亟待法律科学、计算机技术科学与数据科学等多学科领域内的学者与研究者共同探究与解决.

1.2 法计算学的定位

计算法学是国内当前对法律的定量化研究的最新成果, 但本文仍认为这一概念违背了对法律进行数据化或量化延伸的初衷, 甚至会造成未来研究过程中逻辑的混乱. "计算法学", 在词语的构成上系偏正结构, "计算"为定语, 主成分则落在"法学"之上, 与经济法学、民商法学等部分法学的概念具有表现形式上的相似性, 均是以某一特定的社会生活领域为研究对象, 而以法律科学作为对该社会领域进行研究的手段.在这一意义上, 计算法学的内容应是对计算机科学与数据科学领域内的相关权利进行保护或利用过程中产生的法律问题进行的研究, 其本质上是纯法学研究, 计算科学仅是作为研究对象, 而并非提供技术支持的研究手段.故而若以"计算法学"作为对法律法学数据化的研究方法, 极易混淆研究手段和研究对象, 在未来更易造成体系庞杂错乱的困境.而反观作为实证法学领域内的若干研究方法, 其名称均为"法某学"或"法律某学", 如法经济学、法社会学等, 而非以计算法学等为代表的"某法学".据此, 本文提出法计算学的概念.

定义1  法计算学:或称法律计算学, 即以法学理论与法律实践中的问题为出发点, 运用计算机科学和数据科学等领域内的基本原理与技术, 提取、分析、检验、预测社会法律关系及其相应制度的内容、结构、价值、运行及发展.

从以上定义可以看出, 法计算学作为法学与计算科学学科交叉下的产物, 其属于将法律进行数据化、智能化驱动的范畴.从其最本质的特征入手进行理解, 即是以计算科学理论与技术为研究手段, 以法律本体作为研究对象或目标, 在对构成法律的各要素实现数据化处理的前提下, 将所得的数据加载在信息化手段与数据科学的各类算法等驱动之上, 实现对法律的智能化判断、管理与合理预测.

1.3 法计算学的本质:法律关系的数据化

在从计量法学到计算法学的演变过程中, 研究者们对法学的数据化研究虽有所深入, 但均未把握法律科学的本质, 故而该问题应在本文所提出的法计算学领域中予以解决.法计算学以法律科学为研究对象, 而法律科学最本质的特征即是对法律关系的研究.在这一意义上, 法律的数据化驱动就是对法律关系实施的数据化转变, 实现法律关系的可计算化.

在实现法律关系的数据化转化这一目标的过程中, 所采用的主要研究手段应当是寻求法律关系与定量数据间的融合点与连接点, 将法律关系与数理算法自然地建立联系, 从而才能实现对法律计算的普适应用.在此过程中, 切不可为了追求数据化驱动所带来的便利, 而突破法律关系数理上的模糊性本质对法律关系进行不当的数据化加工, 由此单纯地将法律问题转化为可计算的问题或开展数学建模分析, 不仅容易造成论证上的逻辑谬误, 更可能脱离对法律法学进行研究的基本价值取向.反之, 则可在一定条件下兼具定性与定量研究, 在寻求学科交叉连结点的基础上, 对法律关系进行自然地、"柔性"地数据化转化.

2 法律决策与智能算法的对应 2.1 涵摄分类:法律适用的算法

法律适用的方法是律师等法律工作者应用法律条文的基本方法, 是为律师提供智能决策的基础.在传统法律行业中, 律师等法律服务提供者为民众的法律纠纷进行决策的过程即是根据法律条文的规范对纠纷的事实进行判断, 而后依据判断的结论形成相应的对策, 从而最终解决纠纷.在此过程中最为核心的步骤就是对纠纷事实形成法律上的判断, 这一步骤在法律科学的理论上被称为"涵摄"(subsumtion).在涵摄的构成体系中包括经典的演绎推理中的大前提(T)、小前提(S)与结论(R) 3个部分, 大前提即是具体的法律条文规定, 小前提为纠纷案件的事实或社会生活中的事实, 只有当作为纠纷事实的小前提符合法律规定的大前提时, 才能依据大前提的规定推论出相应结论.此外, 法律研究者或工作者的传统思维均是"构成要件"(requirement)思维, 即每一条具体的法律条文包含了多个必要条件, 而只有同时满足所有要件才能得出满足对应法律条文规定的结论.而在上述涵摄推理的过程中, 由于社会现实中的法律规范(T)往往包含了大量的要件特征(M), 因此纠纷案件的事实(S)必须包含所有的要件特征, 才能发生法律规定的法律效果(R).因此, 传统法律推理的具体过程可概括为以下模型:

$ \begin{align*} &\mathrm {T=M^{1}+M^{2}+\cdots+M^{\it n}\to R}, \\ &\mathrm {S=M^{1}+M^{2}+\cdots+M^{\it n}}, \\ &\Longrightarrow \mathrm {S\to R}. \end{align*} $

在上述推理过程中, 涵摄需要解决的问题是, 如何将包含了若干要件特征的案件事实与某一特定的法律条文规范之间建立联系.在数据科学领域, 与法律关系的构成要件特征相对应的概念是"特征属性", 即对最终的观测结果或法律关系结论具有影响性的因素, 且相同类别的因素可划归为若干组或形成连续数值.在这一层面上, 法律涵摄推理可以等价地视作根据已有的法律条文规范或法律关系模型, 对特定的案件事实作出法律效果或法律处理结果上的预测.而预测也是法律推理的基本出发点^[9], 与"利用经验或历史数据, 学习表示事物的模型, 并关注利用模型预测未来数据"^[10]的有监督学习法具有相似之理, 故而完全可利用有监督学习算法实现对法律决策结果的预测性推理.

同时, 由于法律科学的研究对象通常是社会中存在的现象与事实, 在模型的构建上具有不可避免的模糊性与固有的非定量性, 所以对其进行涵摄推理的过程更易作为分类算法进行理解, 即根据特定的案件事实, 将其分类至某类已有的法律关系模型中, 即在国家法律体系中找寻到该法律关系所处的位置, 简而言之就是完成定性分析.在此过程中, 法律关系的所有构成要件就转变为数据样本的特征字段, 以"事实与模型中的应然状态是否符合"作为数据记录中的取值.在这一意义上即可实现了对法律关系的数据化计算, 将法律推理和分析的过程转化为可计算的样本与归类后的数据模型, 使法律科学的传统理论与数据科学领域内的算法形成了有机结合.因此概括而言, 在法计算学的视角下, 一切法律推理的问题其实就是有监督学习下的分类问题.即, 通过对法律关系模型库的搭建实现法律推理数据化的处理操作, 由法律关系模型库与附加在其上的分类算法对特定纠纷案件进行"涵摄分类".

定义2  涵摄分类:根据纠纷案件所包含的事实特征, 依据法律规范所明确的各项构成要件特征, 由数据科学上的算法将案件分类至特定法律关系模型的过程.

涵摄分类在法律科学上属于"法律推理"的范畴, 而在计算机科学领域内, 其本质即是分类算法的应用.故而在法计算学的理论视角下, 涵摄分类的实现过程本质上也是对由一系列具有法律上特征的构成要件所形成的大前提规范及由一系列案件事实构成的小前提, 推出相应的法律分析结论, 而最终经涵摄分类所得的法律关系模型即是的法律推理中的法效果.

对于某一纠纷案件事实而言, 其可拆分成$n$项法律上的构成要件特征, 以一个$n$维数组$Req$[$n-1]$作为应然状态下各特征属性的名称, 各要件属性对应的取值则对应地记作$V_{Req[n-1]}$.记在特定的应用情形$k$的作用下, 其中某一要件特征为$V_{Req[t]}^{(k)}$, 则实然状态下整一纠纷案件的法律要件特征数组可表示为:

$ R{[n - 1]^{(k)}} = V_{Req[0]}^{(k)},V_{Req[1]}^{(k)}, \cdots ,V_{Req[t]}^{(k)}, \cdots ,V_{Req[n - 1]}^{(k)}\} . $

此外, 根据特定算法可对情景$k$下的案件事实进行法律关系的分类, 将最终经涵摄分类所得的法律关系模型记为$M(k)$, 其依据一定的规则可与构成其本身的要件特征数组$R$[$n-1]^{(k)}$之间建立抽象的、模糊的联系.但由于$M(k)$在二维或一维体系下是对某一客观的法律关系模型的指代, 其与案件事实或是构成要件特征之间的联系难以用数据进行量化, 仅可通过文字进行定性地表征, 具有显著的不确定性.因此对$M(k)$的表述更宜置于立体空间中进行描述, 将其视作特定坐标体系中存在的数据点, 从而实现数据化表示与计算.

2.2 律师决策的基本路径

在确定了法律适用的基本方法后, 应当设计合适的算法为律师提供辅助决策.概括地说, 律师的工作任务与需求就是帮助当事人完成诉讼, 且最大程度地提升当事人胜诉的概率.所以若要以人工智能技术实现律师辅助决策, 这一算法设计的根本目标就是帮助律师完成对案件纠纷情况的分析判断, 以便为律师提供有效、可行的提高胜诉率的策略.由于人工智能的实现路径是模仿人类思考问题的方式, 因此律师辅助决策算法也应在充分了解律师处理诉讼案件的思维过程的基础上, 对其进行可计算化的整合与数据化的改进.

律师代理诉讼案件常用的抗辩路径有案由抗辩、程序抗辩和事实抗辩三类, 其中案由抗辩是指对涉案的法律关系所采取的可替代性解决方法, 即法律关系A与法律关系B在结构上较为相近, 但以A为案由进行起诉或应诉相较于B案由而言更有胜诉把握, 所以律师在面对B案由时, 往往会选择向A法律关系进行靠拢, 从而确定案件代理思路的方向性指引.而程序性抗辩与事实抗辩则与具体的案件细节有关, 难以以统一的解决思路方案进行表征, 且人工智能技术的引入也无法对事实或程序等要素进行篡改, 反之则会闯入法律与道德伦理的禁区.因此, 对构成案由的法律关系进行抗辩是目前实现律师服务数据化的最佳路径, 本文也是立足于这一路径, 将其作为联结法律思维与人工智能决策的纽带, 从而为律师辅助决策算法的实现提供基本方向与思路.

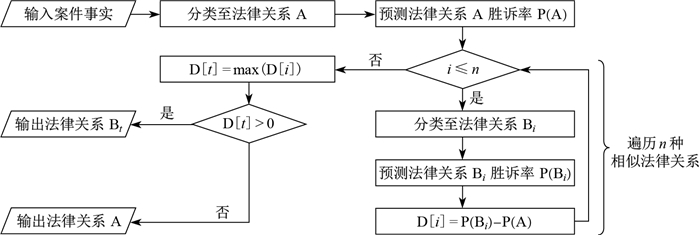
如图 1所示, "案由抗辩"的决策过程大体上可分为两项任务.其一, 对待预测的法律关系进行定性, 寻求特定法律纠纷最为可能的案由A, 以及对原有案件事实适当改变特定要素而形成的其他可能的相近案由${\rm B}_{ i}$; 其二, 以各案由的胜诉率作为依据, 进行案由抗辩的决策, 可分为3个具体步骤: ①预测特定法律关系构成的案由A的胜诉率; ②预测相似法律关系构成的案由${\rm B}_{i}$的胜诉率; ③对比两次所得的胜诉率, 得出决策结果.下文将对此两项任务的实现方案进行详细阐释, 其中将参照C4.5决策树算法构建涵摄分类的具体方法, 实现对法律关系的定性, 再以朴素贝叶斯算法对不同案由下的胜诉率进行预测, 实现案由抗辩的决策.

3 律师辅助决策算法的实现方案 3.1 涵摄分类的决策树算法

法计算学区别于现有的计算法学、计量法学等研究方法的最主要特征, 旨在实现法律关系的可计算化, 即将抽象的、模糊的、通过文字进行描述的法律关系转化为可运算的数据.从上文所述的律师辅助决策的算法路径角度出发, 本文实现法律关系的数据化对应的方式是, 依据一般的数据分析原理为特定类型的法律纠纷建立特征值表, 选取具有代表性的法律关系类型作为最终的数据观测结果, 并分别将构成法律关系结果的构成要件进行拆分, 以形成特征值表的特征属性.在搭建特征值表结构后, 从现实生活中发生的纠纷案件提取要件特征, 录入特征值表形成数据记录, 在记录数总量形成一定规模后, 最终则可依据数据科学上的特定算法对样本进行学习与预测分析.

3.1.1 选取训练数据集

由于目前国内对法律案件与法律关系库的大数据储备明显不足, 也缺少对法律语言进行分词和整合的对应语料库, 故而若需实现以机器学习为手段的智能化法律决策功能, 则只能依靠人工整理相应的数据库样本.本文以表 1所示的结构建立某一类特定法律关系的训练数据库, 记录总行数记为$D$.各行以上标$k$标识数据记录所载的特定法律情形, 字段名$Req$[$n-1]$用以表示该法律关系可能包含的$n$项构成要件特征的名称, $Mode$字段记录情形$k$下的法律关系模型观测结果, 即历史判决结果对应的案由.不同的案由对应不同的法律关系, 根据实际案件的案由可在数据库样本中形成$m$种不同的法律关系, 则可在字段$Mode$的各记录取值中形成$m$维的数组$Mode$[$m-1]$.需要指出的是, 法律关系模型的观测结果的类型为有限个, 虽然在数据集合中以$V_{Mode}^{(k)}$表示第$k$行的观测结果取值, 但$V_{Mode}^{(k)}$的数值最终会出现在数组$Mode$[$m-1]$的成员中.同时, 根据各记录案例实际判决结果的胜诉与否形成字段$Jud$各字段中的记录取值通式可见表 1所示.

在各字段的取值中, 由于构成特定法律关系的特征要件属性往往只有"有"和"无"的二态性, 故而字段$Req$[$n-1]$在各记录行中取值一般可对应地记为"1"或"0".同理, $Jud$字段的取值也一般以"1"或"0"表示胜诉与否.而对于$Mode$字段的取值, 由于这一字段不需要参与具体的数据化运算, 且这一字段实质上是作为记录行的观测结果, 其取值可为任意类型的数据.为便于本文的表述, 在$Mode$字段中本文以从1起始的连续自然数指代各子类法律关系模型, 从而形成特定案件的$Mode$[$m-1]$数组.

3.1.2 生成法律关系模型库

若要实现如上文所述的律师辅助决策算法中前两步的胜诉率预测, 首先需要解决的问题是如何将散乱的案件事实归纳至特定的法律关系模型之中.对此, 本文所建议采取的做法是, 根据前述的数据样本集建立一套完整的法律关系库, 而后即可使用数据科学上的分类算法对某一纠纷案件事实形成归类.由于在律师辅助决策的过程中, 需要律师将构成案件事实的特征逐一输入, 而应然状态下的特征要件数量庞大, 往往是百数量级.因此决策树分类以选择最合适的特征属性作为分支节点为算法的核心^[11], 使之能更为准确地预测每个样本的分类, 且树的规模尽可能小, 恰能与法律辅助决策的目标实现建立合理联系, 成为最为合适的分类算法.当前主流的三类不同的决策树比较如表 2所示, 需要指出的是, 虽然法律关系的特征属性大多是"非是即否"的二态逻辑, 但其也存在着多态性的取值.同时, 对法律上事实的模型归类无需使用回归算法, 其只是一项基础的分类问题, 故而最宜选用C4.5算法予以实现, 其以较为简单的信息增益率作为分类的标识, 也易于与法律专业相关的实践工作人员理解.

本文即参考C4.5的经典算法, 对法律情景下的分类问题进行适当改进, 以以下3个步骤实现对特定法律案件事实的法律关系模型分类.

(1) 合并特征取值相同的记录行

由于法律决策追求的是最大程度内的准确性, 故而用以学习训练的法律关系模型库应当尽可能的全面且精简.在这一需求的要求下, 表 1所示的训练样本集就存在着明显的不足, 应在此基础上对其进行法律场景下的整合优化.若要以决策树实现精准分类, 就应当仅在法律关系库中仅保留最为精确的观测结果记录, 简而言之即是合并所有特征取值完全相同的不同记录行, 对于各不相同的特征取值记录仅保留唯一记录行.而判决结果字段$Jud$实然与法律关系模型的建立并无任何联系, 故而这一字段在法律关系模型库中可以直接删去或忽视.由此, 则可形成理论状态下最为全面的各法律关系模型发生概率的样本库.

在上述合并过程中, 有时会产生特征取值相同而观测结果不同的情形, 此类情况往往是由于法院在判决过程中行使了不同程度的自由裁量权或证据规则上的自由心证主义, 从而导致"同案不同判".对此则建议应采众数原则, 即追求国内绝大多数法院对特定案件所采的高度盖然性态度, 将所有符合特定构成要件的法律关系观测结果中出现次数最多的一则结果作为合并后的观测结果.此外, 出于对数据库中法律关系模型全面性的考虑, 可以人为地补足部分缺少的记录行, 形成理想状态下的一切可能事实记录, 使得法律关系模型库臻于完整.

$ \begin{align} H(Req[t])=-\sum\limits_{i=0}^{{\rm max}(V_{Req[t]} )} {\frac{D(V_{Req[t]} =i)}{D}\cdot \log _2 } \frac{D(V_{Req[t]} =i)}{D}. \end{align} $

(1)

而在合并记录行后, 则可依据上式计算各构成要件特征属性的分裂信息熵, 其中以$D$表示在合并后的法律关系模型库中符合特定条件的记录行数.由此计算所得的分裂信息熵$H$($Req$[$t$])即能直观地表现某一特征属性的复杂程度, 熵的取值越高, 代表在理想状态下的对应法律构成要件越不稳定, 其向其他相近的构成要件变化的可行性就越高.

(2) 计算特征取值的信息增益

信息增益是在数据科学的基本理论中区别于信息熵的对数据属性的另一度量标准, 若某一属性对观测结果的影响程度越为重要, 其所消除的分类的不确定性空间就越多, 即提供的对分类的信息量也就越大^[12].而在法律关系模糊性的视角下, 若某一构成要件$Req$[$t$]对确定法律关系的决定性越为重要, 其对应的要件属性在数据样本集中的形式复杂程度越低, 也即信息增益越大, 在法律涵摄推理的过程中也更易确定.故而本文类比数据科学上的信息增益计算方式, 提出下述对构成要件增益$G$($Mode$, $Req$[$t$])的计算公式.

$ \begin{align} &G(Mode, Req[t])=H(Mode)-H(Mode{\vert }Req[t])\notag \\ = &\sum\limits_{i=0}^{\max(V_{Req[t]} )} {\frac{D(V_{Req[t]} =i)}{D}} \cdot \Big(\sum\limits_{j=0}^{m-1} {\frac{D(V_{Req[t]} =i {\vert }Mode[j])}{D(V_{Req[t]} =i)}} \cdot \log _2 \frac{D(V_{Req[t]} =i{\vert }Mode[j])}{D(V_{Req[t]} =i)}\Big) \notag\\ &-\sum\limits_{i=0}^{n-1}{\frac{D(Mode[i])}{D}} \cdot \log _2 \frac{D(Mode[i] )}{D}, \end{align} $

(2)

其中, $H$($Mode$)表示数据样本中法律关系模型的观测结果类别信息熵, 而$H$($Mode$$\vert $$Req$[$t$])指代特定属性$Req$[$t$]的信息熵.而在数据结果上, 对应的构成要件信息增益恰能体现法律推理过程中, 对大前提与小前提进行涵摄的确定性与准确性.

(3) 递归构造树模型

由前两步计算得出某一构成要件的信息分裂熵与信息增益后, 即可根据信息科学中对信息增益率的概念定义按下式求得该构成要件特征$G_{R}$[$t$]在特定样本数据集中的信息增益率, 形成由所有特征属性信息增益率构成的集合$G_{R}$[$n-1]$.

$ \begin{align} G_R[t]=\frac{G(Mode, Req[t])}{H(Req[t])}. \end{align} $

(3)

根据上述形成的信息增益率集合, 筛选出其中的取值最大一项$Max$($G_{R}$[$n-1])$作为对特定数据集进行首次分类的标签属性, 从而经二叉或多叉形成若干个子数据集, 再度依据上述的3个步骤进行递归分类, 筛选出各自子样本下的最大信息增益率所指向的特征属性, 以此作为子类再分类的标签属性.最终经递归所得的最小子类, 类中所含的法律关系模型观测结果同一, 即符合构造树形成确定分类标准的算法目标, 且各分支节点标签明确.由此即是根据已有的数据样本经学习训练完成了对法律分类决策树的构造, 而后即可依据这一树模型, 对未知结果的案件事实进行涵摄或分类预测.

3.2 辅助决策的朴素贝叶斯算法 3.2.1 特征要件组合的诉讼预测

朴素贝叶斯是基于数学上的贝叶斯定理与对应数据上的特征属性独立假设的分类方法, 经朴素贝叶斯算法所得的数据结论一般系以概率的形式进行呈现^[13].在律师决策等法律应用的情境下, 朴素贝叶斯算法可用以根据历史法律案件的裁判数据, 对未知的案件事实进行法律诉讼上的胜诉率预估或风险分析.其实现流程也是通过对数据样本进行学习训练, 按照样本所体现的规则归纳出特定的概率模型, 从而依据模型、应用模型, 实现对特定未知案件事实的概率结论预测.以下即以表 1中所建立的数据表结构模型为基础, 阐释朴素贝叶斯算法在法律场景下的改进应用, 以及与此对应的律师决策算法的实现.

表 1中建立的法律数据样本基本可满足朴素贝叶斯对案件胜诉与否预测的要求, 但需要指出的是, 由于$Mode$字段系为以C4.5决策树算法进行涵摄分类所用的数据, 在预测胜诉概率的过程中并不必要, 故而在贝叶斯算法的实现数据样本中, $Mode$字段无需参与计算, 而以作为构成要件特征属性的$Req$[$n-1]$字段与诉讼判决观测结果$Jud$字段为主.此外, 由于法律决策要求绝对的严谨性, 故而在数据样本记录的形成方面, 必须选用最高人民法院裁判文书网公布的判决书或指导性案例的判决结果作为记录, 并形成观测结果; 反之, 则难免会造成预测结果不足够准确, 或在一定程度上脱离了中国国情或各类现实性影响因素.由此, 用以构造概率模型的训练样本即可选定, 且参与样本中参与算法运算的特征条件即为各要件特征$Req$[$n-1]$.

朴素贝叶斯算法下的概率模型其实即是根据训练样本中观测结果的先验概率预测后验概率, 但先验概率的计算过程中需假设各特征条件相互独立, 不具有交叉影响关系, 好在这一前提在法律场景中基本都能予以符合, 法律科学理论中的各构成要件也确实基本均为独立要件.故而在这一前提下, 对于涵摄分类下符合第$k$行所有构成要件特征的未知纠纷, 其已知的事实特征要件组合$R$[$n-1]$$^{(k)}$, 可推论出以下先验概率的计算公式.其中, $P$($Jud$=1)表示所有数据记录的观测结果中胜诉的概率, $P$($Req$[$n-1]=R[n-1]^{(k)}\vert $$Jud$=1)表示符合事实特征集合中各特征取值条件下, 各自特征所对应的胜诉概率.

$ \begin{align} P(Jud=1)=\frac{D(V_{Jud} =1)}{D}, \end{align} $

(4)

$ \begin{align} P(Req[n-1]=R[n-1]^{(k)}{\vert }Jud=1)&= \prod\limits_{i=0}^{n-1} {P(Req[i]=R[i]^{(k)}{\vert }Jud=1)} \notag\\ &= \prod\limits_{i=0}^{n-1} {\frac{D(V_{Req[i]}=R[i]^{(k)} {\vert }V_{Jud} =1)}{D(V_{Jud} =1)}} . \end{align} $

(5)

此外, 还需要计算符合事实特征集合中各特征取值时的全概率$P$($Req$ [$n-1]$=$R$[$n-1]^{(k)})$, 即各条件特征取值时的胜诉概率与败诉概率之总和, 计算式如下所示:

$ \begin{align} P(Req[n-1]=R[n-1]^{(k)})&=\sum\limits_{i=0}^{\max(V_{Jud} )} {(P(Jud=i)\cdot P(Req[n-1]=\\ R[n-1]^{(k)}{\vert }Jud=i))} \notag\\ &=\frac{D(V_{Jud} =1)}{D}\cdot \prod\limits_{i=0}^{n-1} {\frac{D(V_{Req[i]} =R[i]^{(k)}{\vert }V_{Jud} =1)}{D(V_{Jud} =1)}} \notag\\ & \quad +\frac{D(V_{Jud} =0)}{D}\cdot \prod\limits_{i=0}^{n-1} {\frac{D(V_{Req[i]} =R[i]^{(k)}{\vert }V_{Jud} =0)}{D(V_{Jud} =0)}} . \end{align} $

(6)

由此即可根据贝叶斯定理, 从先验概率与全概率的结果中推论出特定法律关系模型下的胜诉率概率模型, 这一概率模型的现实意义即是将历史诉讼的判决结果与未知的法律案件可能的处理结果建立了一定程度盖然性的联系, 使前者为后者提供了合理的预测.

$ \begin{align} P(Jud=1{\vert }Req[n-1]&=R[n-1]^{(k)}) \notag\\ &=\frac{P(Jud=1)\cdot P(Req[n-1]=R[n-1]^{(k)}{\vert }Jud=1)} {P(Req[n-1]=R[n-1]^{(k)})} . \end{align} $

(7)

如上式所示, 通过此式对特定特征要件组合所得的后验概率, 即是根据其构成的法律关系构成要件预测其在诉讼中的胜诉率.当胜诉概率高于0.5时, 一般地即可认为特定法律案件在理想状态下更趋于有把握在法律诉讼中获得诉求的支持.

3.2.2 要件组合的合理转化

在前文的论述中, 本文搭建的法律关系模型库中的所有记录都认为是某一法律部门领域内的子类法律关系模型, 模型库整体则构成了该法律部门内全部可能的法律关系的集合.倘若将模型库中所涉及到的$n$项构成要件特征$Req$[$n-1]$引入立体空间, 则可以得到一个$n$维的坐标体系, 每一维度分别对应一项要件特征.而在此"法律关系坐标系"中可落下若干个法律关系数据点, 分别对应在模型样本库中的所有记录, 由此就能实现对法律关系从二维数据表向立体空间构型的转化.

定义3  法律关系坐标系:以空间中任意点为原点向空间以平均的角度引出若干分别标识特定法律关系中构成要件的射线, 并以此类射线为坐标轴, 形成的用以标识法律关系的立体参照系.

在此转化关系的作用下, 一切无论是历史数据或未知的案件事实, 其对应的法律关系观测结果或预测结果$M(k)$均可在这一坐标体系中以法律关系数据点的形式予以表征, 记作:

$ \begin{align*} M(k)\;(R[0]^{(k)}, R[1]^{(k)}, R[2]^{(k)}, \;\cdots\;, R[n-1]^{(k)}) . \end{align*} $

根据本文所需实现的律师决策算法的要求, 需要在根据朴素贝叶斯算法计算出特定法律案件事实在诉讼中胜诉率的预测结果的基础上, 寻求与该事实对应的法律关系模型相似的其他法律关系模型, 并逐一再次预测胜诉概率.这一相似关系在法律关系坐标系下的空间几何意义, 即是与该法律关系模型在坐标系中对应的数据点距离相近.由此, 判断若干法律关系模型相似性的法律问题即转化为求解空间中两点间距离的数学问题.本文将以欧式距离公式对此进行分析,

$ \begin{align} d(M(k), M({k}'))=\sqrt {\sum\limits_{i=0}^{n-1} {(R[i]^{(k)} -R[i]^{({k}')})^2} }. \end{align} $

(8)

上式即是根据欧氏距离的计算方法在法律关系坐标系中两法律关系数据点$M(k)$与$M(k')$之间距离的应用.在遍历含有$D$行历史记录的模型库中所有的法律关系模型观测结果记录后, 即可求得$D-1$项两法律关系模型之间的相似性距离差, 在此基础上对距离进行升序排列.以前$q$项作为认定两法律关系具有相近关系的阈值, 分别记录前$q$项两点间距离差在数据训练集中所对应的记录行$k'$, 从而定位到第$k'$行形成的特征要件数组$R$[$n-1$]$^{(k')}$, 以及由其涵摄分类所得到的法律关系模型$M(k')$.

案件事实从原法律关系模型$M(k)$重定位到$M(k')$的动态过程, 意义在于辅助律师检索与涉案案由所指向的法律关系相近的其他法律关系, 而便于向新法律关系靠拢.因此, 在这一过程中有两方面的限制应当受到关注: ①转化过程的实质是案件所处法律关系中某一或若干构成要件特征的取值发生了变化, 故而这特定的一项或多项要件属性应当具备可改变性, 即其并非无法改变的客观事实, 而通常是具有一定主观性的抽象要件; ②被改变的特定要件特征属性的分裂信息熵$H(R$[$t$]$^{(k)})$应具有一定规模, 使得这一项或多项属性易于向不同于原取值的其他取值倾斜.

3.2.3 对新要件组合的再预测

律师辅助决策算法的最后一步就是对通过欧氏距离公式遍历所得的一定阈值内的若干新特征要件组合计算其胜诉概率, 这一过程与前述朴素贝叶斯算法的实现相同, 不再重复赘述.记某次对数据点之间距离进行遍历时确定的新法律关系模型阈值个数为$q$, 则有各新特征组合前后两次胜诉率之间的差值构成的数组$\Delta P $[$q$ -1].

$ \begin{align} &\Delta P[q-1]=P(Jud=1{\vert }Req[n-1] = R[n-1]^{({k}'^{(q-1)})})\notag\\ & \qquad -P(Jud=1{\vert }Req[n-1]=R[n-1]^{(k)}). \end{align} $

(9)

取数组中的最大项$\max$($\Delta P$[$q-1$])所指向的$k'$, 其对应的构成要件组合经涵摄分类所得的法律关系模型$M(k')$即为理想状态下, 最有助于律师提升案件诉讼把握程度的案由.至此, 本文即已依据数据科学与管理科学上对"数据—模型—决策"的基本思路要求^[14], 实现了通过在特定数据上构建适当的模型, 为律师提供辅助决策算法的目标.而针对$\max$($\Delta P$[$q-1$])的计算结果, 大体上可以分为正数与非正数两类, 对于非正数结果而言, 其意义就是原法律关系模型对应的案由已是理想状态下的最佳诉讼路径, 而无需替换其他要件形成其他法律案由; 而对于正数结果而言, 就表明原法律关系模型在一定程度内仍可以提升胜诉概率, 并非最佳诉讼策略, 但由于同一法律关系模型的内部构造可能有多种形式, 所以对提升胜诉概率的具体策略也可细分为两种.

(1) 对于$M(k)$与$M(k')$同属于一类法律关系模型$Mode$[$t$]的情况, 其代表着虽然最佳诉讼策略所指向的法律关系模型与现有的事实特征要件组合所预测的法律关系模型相同, 但由于法律关系内部构造不同, 不同的特征要件组合也可能指向同一法律关系模型, 所以从结论已然是最佳状态的角度出发, 可以在法律关系模型内部, 对特定要件进行适当改进, 从而最大程度地提高诉讼的把握度;

(2) 对于$M(k)$与$M(k')$所属不同的法律关系模型的情况, 这就意味着律师原先选定的案由并非诉讼最佳策略, 有必要在合理限度内修改案件的要件属性, 从而趋近于最佳诉讼策略所对应的特征要件组合, 并以此进行涵摄分类, 确定更为恰当的诉讼案由.

4 决策实验与结果验证 4.1 实验设置

本文以交通事故纠纷为例, 对特定未知的案件进行诉讼辅助决策.由于法律关系往往具有复杂性, 构成要件的数量也较为庞大, 本文以其中较为简易的一则含有7项要件特征的子类法律关系为例, 将其全部纳入数据样本并参与算法实现.

在实验数据集中, 训练样本数据集字段中的特征要件数组为$Req$[6]={"公共路面", "财产损失", "人身伤害", "责任认定", "事实异议", "故意情形", "严重情形"}, 各数组内元素的实际取值均为1或0, 用以表示该特征要件在法律案例记录中的存在与否.由法律关系模型观测结构构成的数组$Mode$[4]={"应当报警的交通事故", "一般交通事故", "具有特殊过错情形的交通事故", "可以协商解决的交通事故", "非交通事故"}.实验训练数据集中共有133条法律案例历史数据, 经合并特征取值相同的记录行, 并根据理想状态补全所有可能的情形记录后, 形成了108行的法律关系模型库数据集, 用以对交通事故纠纷构造准确的涵摄分类决策树, 数据集中各特征属性字段与对应的法律关系观测结果模型类别的记录行数关系如表 3所示.

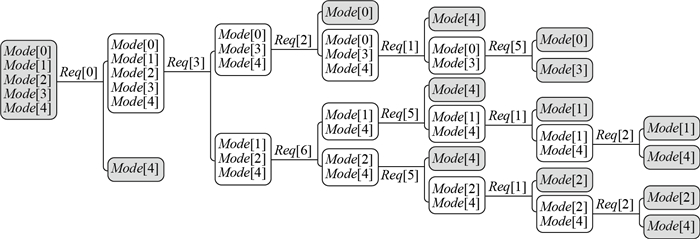
根据此统计表与前文所述的决策树构造算法, 得到第一次分叉时各属性的信息增益率数组$G_{R}$[6]={0.452, 0.033, 0.120, 0.255, 0.039, 0.090, 0.092}, 故而即以数值最大项指向的特征属性字段$Req$[0]作为首次分叉的标签, 从而在二分后再度进行递归计算与循环, 最终可得的交通事故纠纷法律关系模型决策树如图 2所示, 以此作为律师决策时对案件事实涵摄分类的依据.

本文以上述形成的模型库为基础进行了8次法律决策实验, 在此以其中的一次实验为例详细阐释实验设置的过程, 其他实验结果在后文予以统一罗列.在示例实验中, 需要预测与决策的未知法律案件事实是"两车在公共路面上发生相撞, 除两车不同程度地受损外, 还造成了一人轻伤, 事故后交警对此出具了事故责任认定书", 根据其字面表述经归纳形成的特征要件组合为$R$^[6]={1, 1, 1, 1, 0, 0, 0}.而依据决策树的涵摄分类, 其对应的法律关系模型应是$Mode$[1], 即为一般交通事故纠纷.在此基础上, 对该案件在法律关系坐标系上的数据点$M$(0)周边的其他法律关系数据点进行遍历, 得出以下5项距离均为1.00的数据点, 并列属于距离原法律关系模型最近的数据点, 可被认定具有高度相似性.

4.2 实验结果

实验依据交通事故案件训练样本数据集中的133条数据记录, 在朴素贝叶斯算法的支持下, 对符合法律关系数据点$M$(0) (1, 1, 1, 1, 0, 0, 0)及其相近的其他数据点对应的特征要件组合预测其案件的胜诉概率, 所得的历史数据中特征属性与判决结果的对应关系如表 5所示.

根据上表中的数据记录行数对应关系, 计算得某一特定的特征组合或法律关系数据点的先验概率$P$($Req$[$n-1]=R[n-1]^{(k)}\vert $$Jud$=1)$\cdot P$($Jud$=1)与全概率$P$($Req$[$n$-1]=$R$[$n$-1]$^{(k)})$, 从而预测出对应数据记录所指向的案件的后验概率, 即理想状态下可能的胜诉率.根据前文所述的辅助决策算法, 最终所得的与实验所需决策的对象相关的所有数据点的胜诉率预测如表 6所示.

从上表的实验结果可知, 原有的特征要件组合$M$(0)胜诉概率为72.99%, 而与之相近的另一特征要件组合$M$(2)胜诉概率为74.27%, 达到相近的所有法律关系模型中胜诉概率的最大值.即, 若律师将实验案件事实向特征要件组合$M$(2) (1, 1, 1, 1, 1, 0, 0)靠拢, 则可以在一定程度内提升理想状态下的案件把握度.对比$M$(0)与$M$(2)在要件特征上的构成不同可知, 这一靠拢过程实质上代表着将$Req$[4]从取值0变更为1, 也即对于某一交通事故案件而言, 其当事人对事故的成因等由无异议变更为有异议.这一变更是当事人主观态度的变更, 并非是对客观事实的歪曲或捏造, 没有触及法律的限制性红线, 故而具有提高胜诉率的合理性与可行性.

由此得出, 示例实验的最终结论以文字进行表述, 即对于两车在公共路面上发生相撞, 造成人身伤害与财产损失, 且交警出具了事故责任认定书的交通事故, 若当事人对事故发生的成因及经过在主观上存在异议, 则在同等理想情况下, 该案仍以一般交通事故纠纷为案由向法院提起诉讼, 案件在诉讼过程中的胜诉概率将提升1.3%.全部的8次决策实验结果记录如表 7所示.

4.3 决策准确度验证

对于实验结果准确与否的验证问题, 机器学习领域的常见方法均是以一定的系数作为检验实验结果数据一致性的衡量参数^[15].但由于法律法学系社会科学下的产物, 以主观性、模糊性、抽象性为其本质特征, 法律决策的结论本身也不存在是非对错之分, 只有以人的意志为标准衡量其"合理"与否, 故而无法通过定量比较或分析的方法对实验结果进行准确度的直接论证, 仅能从侧面推测决策结果的可信度, 以下将分别从离散程度统计和吻合度问卷调研两个角度进行验证.

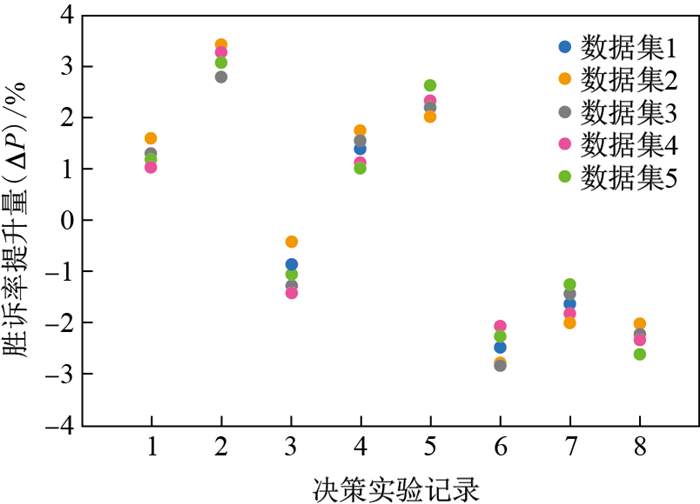
4.3.1 离散程度统计验证

本文通过替换实验所用的数据集的方式进行多次决策实验, 同样以表 7所示的8行特征要件组合记录作为实验样本, 在5组不同的数据集中以C4.5决策算法与朴素贝叶斯算法预测实验样本的胜诉率, 以及经欧氏距离叠加后变更的新特征要件组合的胜诉概率, 并将两次胜诉率之差作为实验结果进行记录, 形成了如图 3所示的以40项实验结果作为数据点的离散统计图.

从上图可以得出的是, 每组特征要件组合对应的5次不同数据集的实验结果数据点均距离较近, 可以认为其离散程度较低, 即在不同数据样本集下的实验结果集中程度较高, 经多次实验均能得到极为近似的实验结果.因此可以推论出, 实验的结果具有相当的稳定性, 并非系偶然得出的结果, 具有较高的准确度与可信度.

4.3.2 吻合程度调研验证

虽然目前对法律关系的数据化分析尚无任何客观的解释工具予以直接参考, 但从主观角度来看, 问卷与访谈调研论证仍是法律法学领域最为有效的决策检验方法.即, 从社会公众与专业人士的视角, 判断该实验结论是否可被社会所认可.本文所述的算法与实验均是以辅助律师决策为目标, 故而对实验结果选取的最为合理的检验者就应当是律师等法律工作者本身.

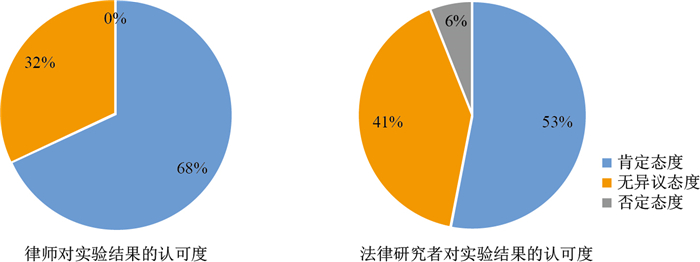
通过对22名律师与17名法学研究者进行问卷调研或访谈调研, 得出的对本次实验结果的认可程度分布情况如图 4所示.从图中可知, 除1名法学研究者对本次实验的结果持否定态度之外, 其余的38名受访者均认可实验结论, 或对结论持不反对的中立态度, 由此可得证实验结果的准确性.即, 本文提出的算法与大多数优秀律师的代理思路与诉讼策略保持高度一致, 并在一定程度上与普通社会民众解决诉讼纠纷所采用的策略相比, 具有相当的先进性与优异性.

5 研究结论与展望

本文基于法计算学的视角, 实现了辅助律师进行诉讼决策的算法, 对C4.5决策树与朴素贝叶斯等算法在法律场景下的应用作了改进.本文提出了涵摄分类与法律关系坐标系的概念, 并以欧氏距离确定法律关系要件特征组合转化的可操作性, 以后验概率的取值确定决策的优异性.最终经实验数据测试及调研验证, 该算法在律师诉讼策略的决定上具有高度盖然性的准确率.由于对于法律关系的构成要件不可避免地存在一定交叉的问题, 以及对其他法律智能应用场景与算法应用准确度标准的研究, 未来进一步研究引入贝叶斯信念网络等更为先进的算法实现优化, 以及计算科学与法学研究者共同探索法律"数据驱动"的问题.