室内定位(Indoor Localization)问题作为基于位置服务(Location-Based Service, LBS)、增强现实(Augmented Reality, AR)、同步定位与建图(SLAM)等应用的关键问题, 是近年来领域内普遍关注的热点.现有的解决方案包括基于WiFi信号强度RSSI(Received Signal Strength Indication)、激光雷达(Lidar)和机器视觉等, 其中机器视觉方案由于更接近人类感知方式、定位精度较高、室内和外场景兼容度高等特点在探索未知环境的应用中格外受到重视; 而RGB-D采集设备的出现使得捕捉到的画面带有环境景深信息, 令立体视觉的获取更为方便快捷.
根据Glocker的定义[1], 视觉定位的解决方案主要可分为基于路标方法LbAs(Landmark-based Approach)与基于图像方法IbAs(Image-based Approach)两类.这两类方案在实用化道路上存在各自的障碍, 例如, 以关键帧图像整体或关键帧图像内特征作为匹配依据的IbAs虽具有较高定位精度, 但图像的引入导致其受视角变化的制约严重, 无法利用不同视角下的相同特征路标实现定位, 而特征地图构建过程中引入的构建误差会给LbAs带来负面影响; 在LbAs中, 以特征点描述子(Point Descriptor)作为路标的解决方案可能因采集设备移动造成动态模糊(Motion Blur)而导致无法准确提取特征, 由于点特征无法全面呈现环境结构, 遮挡所造成的特征消失也将显著影响匹配与定位效果.
虽然早期视觉SLAM及其定位方案受计算资源限制将像素点作为特征首选[2-3], 但高维特征由于在提取时较少受到动态模糊与遮挡问题影响而受到持续关注.通过匹配室内场景中的已知物品来得到地图特征的SLAM++颇具代表性[4], 但这一方案受限于物品种类, 无法识别其预存立体模型库中不存在的物品.相比之下, 平面既是室内场景中最常见的构成要素, 又能通过其组合呈现不同结构, 被认为是优良的全局特征来源.基于平面特征的定位方案有着广阔的发展空间与应用前景.
以此为基础, Shi等利用深度学习为SLAM提供平面特征描述子[5]; Forstner等利用平面匹配来计算路径中位姿(Pose)的持续变化[6]; Taguchi等同时将点与平面作为特征, 并采用RANSAC算法进行匹配与定位[7]; Fernández-Moral等的PbMap定位[8]则使用解释树算法匹配两个由平面组合而成的结构, 实现识别及定位. PbMap定位方法本质为充分利用平面所组成结构而非平面特征本身进行匹配, 对环境结构的理解与基本特征的利用有着独到之处; 另一方面它却受限于运行耗时的限制, 一般仅利用较小视野范围的子图结构进行匹配, 往往需要牺牲识别定位效果以支持实时运行.值得关注的是, 仍有一些基于平面的SLAM系统放弃对平面特征进行复用, 而是选择采用基于关键帧的IbA方式实现定位[9-12].
本文致力于改进PbMap定位方法, 实现基于平面特征的LbA定位方案, 并将曼哈顿世界假说(MW)引入至室内场景的结构匹配来扩大视野范围并提高运算效率, 旨在为平面SLAM系统实时提供可靠的定位结果.本文后续内容组织如下:第1节介绍平面定位的相关概念并分析已有方法; 第2节提出本文定位方案; 第3节给出实验结果并进行分析; 第4节总结全文.
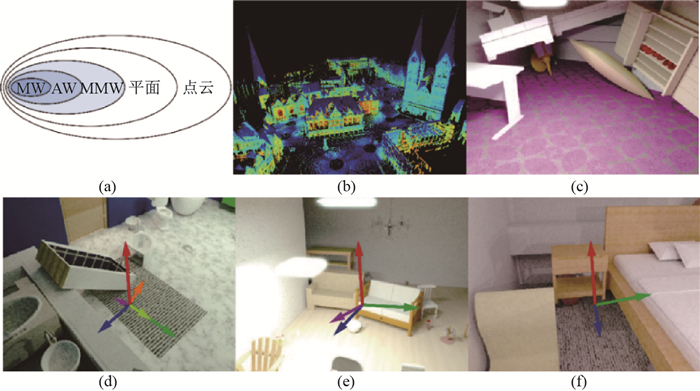
1 相关问题说明 1.1 曼哈顿世界假说MW模型[13]揭示了人造建筑结构的特性, 以三维立体网格的形式更准确地描述了城市及室内结构.之后提出的一系列结构假说模型, 如亚特兰大世界假说(Atlanta World assumption, AW)[14]、混合曼哈顿世界假说(Mixed Manhattan World assumption, MMW)[15]等分别扩展了其对建筑结构特点的描述.总体上, 人们对于建筑环境的描述方式可借助如图 1所示的一系列模型来表示.如图 1(b), 点云作为表征物体的最基本元素可普适地展现外部环境[16], 而平面作为建筑的主要组成要素, 被一系列平面SLAM及定位系统用于描述环境的基本特征, 如图 1(c).在平面的基础上, 曼哈顿世界系列假说模型进一步探索了建筑的结构特点:在MW下, 建筑中存在一个正交的立体坐标系, 建筑内平面的法线与一个坐标轴保持平行, 如图 1(f); 而在AW下, 建筑中存在一个竖直主方向与多个水平的主方向, 建筑内平面的法线与其中一个主方向保持平行, 如图 1(e); MMW则作了进一步推广, 假定建筑中存在一个主要的正交立体坐标系与其他副坐标系组, 建筑内平面的法线平行于某一坐标系的坐标轴, 如图 1(d).曼哈顿世界系列假说、平面及点云分别以不同方式对建筑结构进行了解读, 其相互关系如图 1(a)所示.选择某一假说模型虽然牺牲了部分普遍特征(如平面模型牺牲了点云中的曲面信息、曼哈顿世界系列模型不同程度上牺牲了平面位姿的统计随机性), 但恰当的假说选择也可能为应用带来更多先验信息.
|
图 1 曼哈顿世界系列假说及关系图 Fig.1 Representation of the environment in point cloud, plane model, MMW, AW, and MW |
解释树算法作为一类经典匹配算法, 通过递归计算组件与组件间的关系来确定整体的匹配情况, 常被用于计算二维或三维对象的匹配问题[17].在三维匹配问题中, 三维实体被拆解为多个分块即组件来执行解释树算法匹配, 其算法流程见算法1.算法1中, 一元约束判断源实体中组件

|
在基于平面特征的定位应用中, 在目标地图中识别出当前平面集所组成的结构, 就可以看作立体匹配的问题使用解释树算法进行计算, 得到当前地图与目标地图间对应平面的配对关系并实现定位.
1.3 PbMap定位平面定位模块利用由视觉里程计(Visual Odometry, VO)连续配准的平面特征地图与目标地图进行匹配实现定位, 同时定位得到的位姿也进一步地为VO修正误差提供参考. Fernández-Moral采用解释树匹配算法实现了利用平面特征的识别与定位[8], 以下从其建图、识别与定位环节简要介绍该方案.
1.3.1 PbMap建图由于解释树算法匹配是由平面所组成的结构, 故界定结构的范围是必要的.在人类认知中, 结构表现为相邻平面之间的局部关系, 所以在解释树算法匹配两个结构之前, PbMap定位方案在当前地图与目标地图中分别划分两个具有一定量平面的邻域以供匹配. PbMap连通图的构建将特征地图中彼此邻近、联系紧密的平面特征相互联接, 形成的连通图含有不同度的结点.结点度值高, 即联系紧密的平面特征集合作为连通图的枢纽结点, 能与其相邻结点平面组成更为复杂的结构, 更富有辨识度.于是, 在特征地图中构建PbMap地图并划分子图的目的在于, 在特征地图中构建连通图, 找出富含邻居结点即结构特征丰富的平面组, 并将其构建成邻域子图进行解释树匹配.
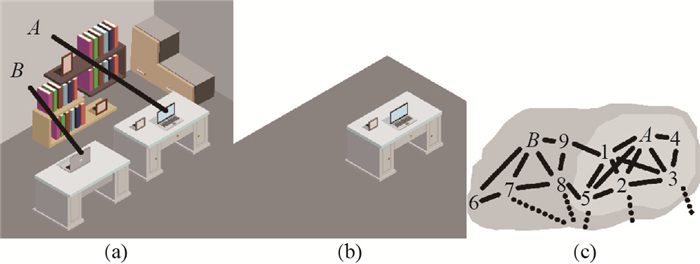
设备在探索环境的过程中将当前帧内所检测到的每一平面置入地图, 并同步检测该平面与其他所有平面的邻近关系.如图 2(a)所示, 若当前帧提取到
|
图 2 PbMap建图过程 Fig.2 Construction of PbMap |
在划分得到当前地图与目标地图中的子图结构后, 就可以采用解释树匹配对当前子图结构在目标地图中进行识别.当前子图与目标子图中的平面集合即为待匹配组件集合
| $ \begin{align} \mathrm {Similarity}(H_u^c, H_v^t)>th_{\rm{hue}}, \end{align} $ | (1) |
| $ \begin{align} th_{\rm{area-lower}}<\frac{a_u^c}{a_v^t }<th_{\rm{area-upper}}. \end{align} $ | (2) |
二元约束定义为
| $ \begin{align} |\mathrm {arccos}(n_u^c\cdot n_i^c )-\mathrm {arccos}(n_v^t\cdot n_j^t )| <th_{\rm{angle}}, \end{align} $ | (3) |
| $ \begin{align} |(C_u^c-C_i^c )-(C_v^t-C_j^t ) | & <th_{\rm{dist}}, \end{align} $ | (4) |
| $ \begin{align} |n_u^c\cdot (C_u^c-C_j^c )-n_v^t\cdot(C_v^t-C_j^t ) | & <th_{\rm{ortho}}, \end{align} $ | (5) |
设
带有一元约束与二元约束的判断过程比较了以平面特征为结点的两个子图的匹配关系, 其中一元约束比较在
在将MW引入至平面定位问题之后, 曼哈顿主方向可以从多个方面为PbMap定位服务, 提升其运算效率与识别效果.下面以PbMap定位的一般过程为序, 对传统方法的不足进行分析并给出本文的改进方案.
2.1.1 PbMap建图第1.3.1介绍了将平面地图联结成子图进行匹配的一般方法.然而在实际应用中, 每一帧的定位过程通常含有大量的重复计算.例如在如图 2(a)所示的一帧画面中, 平面
为在保证识别定位效果的同时提高搜索效率, 在建图过程中, 本文将一帧中检测到的所有平面及其邻居面都置入同一个子图, 如图 2(c)中的深灰底色部分.令平面
在将单帧检测到的平面置入同一子图以排除多次搜索过程后, PbMap定位会受限于指数级增长的子图匹配耗时, 因大范围子图内平面特征数量的增多而无法实现实时运行.由于室内场景中曼哈顿主方向信息的存在, 在子图匹配过程中本文将不同的主方向作为竖直方向, 分为3种情况进行解释树搜索, 并在每组搜索中利用平面在曼哈顿主方向下的属性信息滤除误匹配对.子图范围内的平面所呈现的MW坐标系主方向之一被选取为子图匹配的竖直方向, 并进而确定每个平面在当前MW坐标系下的附加位置信息:平面类型与沿MW坐标轴尺寸.平面类型包括: ①水平平面; ②满足MW的竖直平面, 即与非竖直方向的某主方向保持垂直的平面; ③仅满足AW的竖直平面, 即仅与假定竖直方向保持平行的平面; ④随机位姿平面, 即不与任一主方向保持垂直或平行的平面.
每一平面沿3个主方向轴下的长度集合被定义为
| $ \begin{align} k_u^c = k_v^t , \end{align} $ | (6) |
| $ \begin{align} th_{\rm{size-lower}} < \frac{s_u^c}{s_v^t}<th_{\rm{size-upper}}. \end{align} $ | (7) |
而二元约束的判断同公式(3)、公式(4)和公式(5).
由于平面基本属性与子图竖直方向的选取无关, 所以3组搜索中的基本属性约束只需执行一次.在实际实现中, 当前地图与目标地图平面匹配对间的一元约束与二元约束结果都用索引表进行记录, 仅出现在当前帧中的平面与其他平面的约束判别结果会进行计算并在索引表中更新.
另外, 由于目标地图已知正确的竖直方向, 所以在选取错误主方向为当前子图竖直方向时, 水平平面的匹配对总是误匹配对.所以在实际运行搜索树匹配时, 本文要求每组匹配对结果都将一对水平平面匹配对作为根节点, 从而使错误竖直方向下的匹配从误匹配对开始执行, 令匹配对数量更少, 更快得到结果并确定竖直方向的选取是否正确.
每一组假想竖直方向下的匹配过程见算法2.匹配过程采取当前地图中子图的平面集合法

|
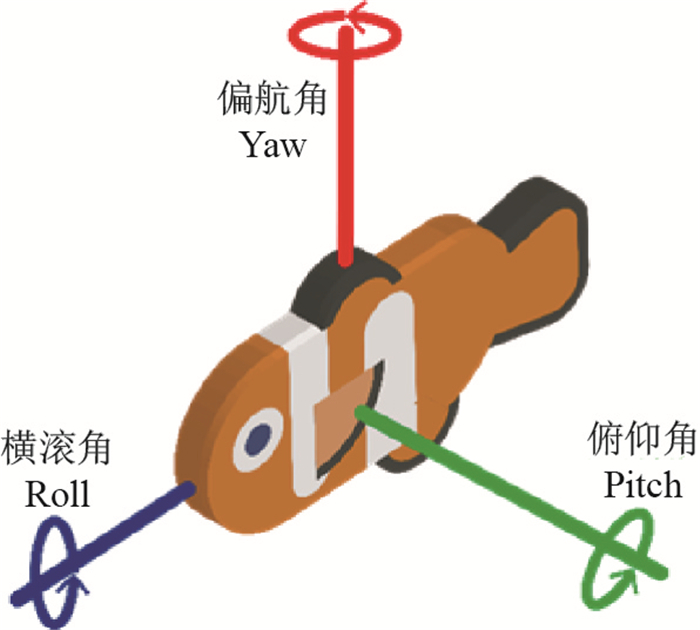
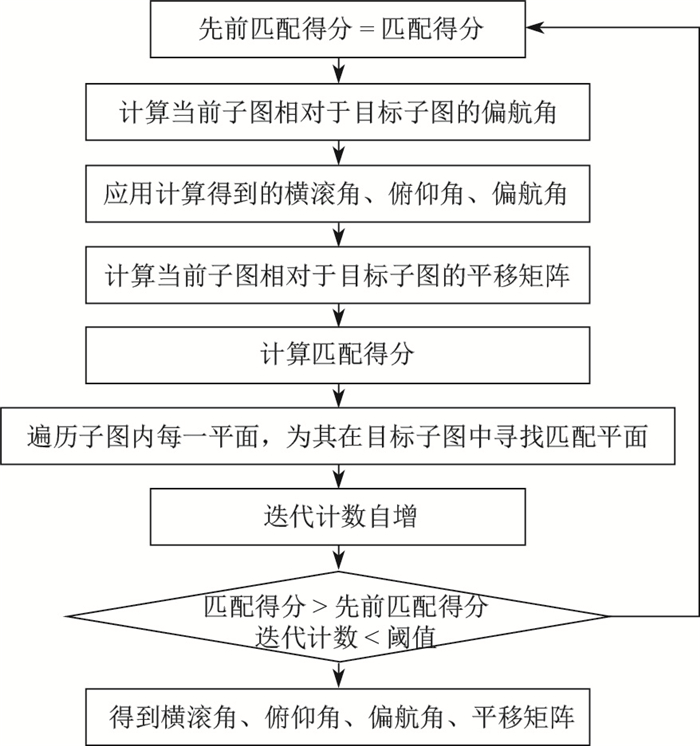
在得到候选匹配对与候选竖直方向后, 当前子图的候选竖直方向与目标子图的竖直方向就可以进行对齐.根据水平平面匹配对的法向信息, 可以确定竖直轴的指向, 即如图 3所示的横滚角与俯仰角可以确定.于是匹配就可以从3轴位置坐标、横滚转向、偏航转向及俯仰转向未知的6自由度问题降为4自由度问题, 其计算流程如图 4所示, 其中对子图匹配程度的评分
| $ \begin{align} S =\sum\limits_{u=1}^n\frac{a_{\rm{inter}} (P_u^c, P_v^t )}{\sum\limits_{i=1}^n a_i^c}\cdot {\rm{Similarity}}(H_u^c, H_v^t )\cdot \frac{2}{1+{\rm e}^{\alpha|D_{u, v} |}}, \end{align} $ | (8) |
| $ \begin{align} D_{u, v} =n_u^c\cdot(C_u^c-C_v^t). \end{align} $ | (9) |
|
图 3 姿态角术语 Fig.3 Terminology of Euler angles |
|
图 4 平面配准流程 Fig.4 Flow chart for plane registration |
计算流程, 首先将解释树搜索中得到的平面匹配对作为初始时的平面匹配对, 计算相应的位姿变换矩阵与匹配得分, 进而在目标子图中查找与当前子图中每一平面
在每次迭代的匹配度评定中, 不仅解释树算法中得到的平面匹配对被纳为考量目标, 迭代中新增的平面匹配对也同步地加入至匹配对集合中.两子图的匹配程度计算从平面重叠面积占比、色度相似程度、距离等3个角度进行评定.公式(8)中,
在传统的基于点特征的定位方法中, 通常将位姿计算统一看作为6自由度的定位问题.由于点特征无法揭示环境结构信息, 即使前一时刻的成功定位可以确定建筑结构坐标轴主方向, 但VO(Value Object)的误差同样会造成当前帧建筑结构主方向与前一时刻存在偏差.随着时间推移, 误差将持续累加甚至引起地图构建错误.然而, 由于从平面特征中能够解读环境的结构与法向信息, 在行进路径中的每一时刻都能从小范围邻域内的平面特征中提取出MW环境结构的主方向.
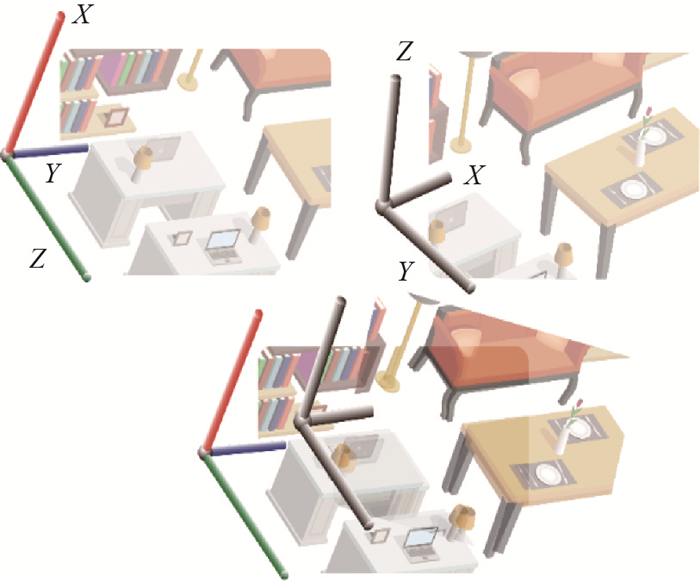
若行进路径中两相邻帧如图 5所示, 前一帧经过成功定位后已知竖直方向为坐标系轴
|
图 5 行进路径中的主方向确定 Fig.5 Determination of main directions in subsequent trajectories |
在获悉轨迹中后续每一时刻的竖直方向指向后, 定位过程就拥有更多条件信息, 从6自由度定位简化为4自由度定位问题.值得注意的是, 问题的简化并不受限于定位算法的选择, 在平面、线条特征地图构建的过程中加入曼哈顿主方向计算即可实现简化.具体表现为第2.1.2所介绍的识别过程, 仅需一组解释树匹配搜索过程, 根据竖直方向参考排除的平面匹配对也降低了子图识别耗时.当VO连续正常运作时, 一条行进路径上的定位平均耗时将接近4自由度定位的耗时水平.
3 实验评估为了评估本文定位方法在实际应用中的效果, 这一节给出了场景实验与结果分析.
实验以微软Kinect 1摄像头为输入设备, 并采用搭载2.5 GHz Intel i5的计算机作为实验运行设备.
由于现有的公开SLAM数据集场景轨迹与平面要素较少, 本文采用现实生活中的10个房间作为实验场所.对每一房间, 都采集20条不同的运动轨迹所捕捉到的RGB-D图像, 以测试基于特征定位方式从不同位姿识别场景的能力.
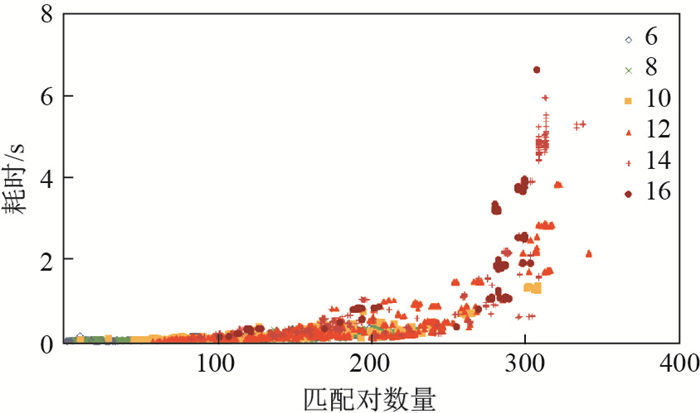
表 1展示了采用不同邻近阈值的PbMap定位方法与本文定位方法在陌生场景下的初始时刻6自由度的定位表现.由表 1可知, 单一子图搜索的平均耗时与每帧子图搜索的平均耗时(表 1中左起第5列、第6列), PbMap定位平均每帧执行约2轮子图搜索.这代表着在实验中, 平均每帧对第二个捕捉到的平面执行子图搜索后才能定位成功, 这也造成了重复的计算开销.随着采用更大范围的邻近阈值以构成更大视野范围的子图, 定位所需路径长度逐渐缩短, 而搜索耗时与总耗时也在相应地以指数级增长.子图匹配耗时与子图内特征匹配对数量的关系如图 6所示.在解释树子图匹配过程中得到匹配对数量相同的情况下, 匹配耗时随子图内特征匹配对数量呈指数级增长; 而在子图内特征匹配对数相当的情况下, 得到匹配对更多的解释树匹配过程相对耗时更高.这使得平面定位无法完全利用完整视野范围内的所有特征构造子图进行匹配, 只能选择较小的子图结构, 在牺牲定位表现的前提下达到实时运行.
| 表 1 初始定位结果 Tab. 1 Results form initial localization |
|
图 6 子图匹配耗时与匹配对数量关系 Fig.6 Subgraph matching time-plane matches |
本文所采用的平面定位策略由于将每帧捕捉到的所有平面置入一个大的子图, 邻近阈值仅作为连接平面特征之用, 识别过程所匹配的子图大小规模主要由视觉探测设备的视野范围所决定.所以, 这即等效于PbMap的邻近阈值取值为略小于探测设备视距的浮动值.在本次实验中, 子图的大小范围平均约为3.71 m, 并与邻近阈值分别为1 m、2 m、4 m时的PbMap解释树匹配定位进行比较.在与4 m级邻近阈值的PbMap定位过程具有相当的子图内特征数量时, 其将解释树搜索过程分拆为3组不同竖直方向选取下的解释树搜索, 匹配耗时随特征数量呈指数级增长, 含少量特征的小组匹配方案可有效提升搜索速度, 在3组搜索总特征匹配对数增多的情况下具有更短的搜索耗时.另外, 由于每帧不再需要迭代搜索不同平面的子图, 不同子图结构的多次匹配搜索也可节省至每帧一次, 从而使得子图结构的匹配识别利用视野内更广范围的同时提高了运算效率.同时在后续的识别定位中, 由于初始位姿确定后的竖直方向参考信息, 识别定位的时间开销又进一步得到削减.定位轨迹所有时刻的平均定位数据如表 2所示.本文提出方法中的最大定位耗时即为初始定位时的最大耗时.在每帧的子图匹配中引入更多特征后, 定位的精度与成功率都会随之提高, 而随着行进距离的持续增加, 定位耗时趋近于后续4自由度定位耗时, 降低了整条路径上的平均定位耗时.
| 表 2 路径定位平均结果 Tab. 2 Average result of localization on the trajectory |
实验中, 划定子图的邻近阈值
随着基于高层次特征SLAM的发展, 本文旨在为SLAM系统提供基于平面特征的定位系统模块.将曼哈顿世界假说引入平面定位过程, 并以PbMap定位方法为基础提出了改进方案:采用大范围子图进行特征匹配以排除单帧内反复执行的子图识别; 利用曼哈顿世界假说模型分解初始位姿计算的解释树匹配, 以降低大范围子图的搜索时间开销, 并将行进路径上的后续定位简化为4自由度的定位问题.本文方案更充分地利用视野内的更多特征, 能更早地得到定位结果并削减搜索耗时, 在定位效果与运行效率上都实现了一定程度的提升.实验显示, 大范围子图结构使定位所需轨迹距离更短, 而曼哈顿世界假说的引入有效地提高了运算效率, 能完整地利用现有RGB-D采集设备的视野范围, 并更好地支持实时应用.
| [1] |
GLOCKER B, SHOTTON J, CRIMINISI A, et al. Real-time RGB-D camera relocalization via randomized ferns for keyframe encoding[J]. IEEE transactions on visualization and computer graphics, 2015, 21(5): 571-583. DOI:10.1109/TVCG.2014.2360403 |
| [2] |
SE S, LOWE D G, LITTLE J J. Vision-based global localization and mapping for mobile robots[J]. IEEE Transactions on robotics, 2005, 21(3): 364-375. DOI:10.1109/TRO.2004.839228 |
| [3] |
MUR-ARTAL R, TARDÓS J D. Orb-slam2:An open-source slam system for monocular, stereo, and rgb-d cameras[J]. IEEE Transactions on Robotics, 2017, 33(5): 1255-1262. DOI:10.1109/TRO.2017.2705103 |
| [4] |
SALAS-MORENO R F, NEWCOMBE R A, STRASDAT H, et al. Slam++: Simultaneous localisation and mapping at the level of objects[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2013: 1352-1359.
|
| [5] |
SHI Y, XU K, NIEßNER M, et al. Planematch: Patch coplanarity prediction for robust rgb-d reconstruction[C]//Proceedings of the European Conference on Computer Vision (ECCV). 2018: 750-766.
|
| [6] |
FORSTNER W, KHOSHELHAM K. Efficient and accurate registration of point clouds with plane to plane correspondences[C]//Proceedings of the IEEE International Conference on Computer Vision. 2017: 2165-2173.
|
| [7] |
TAGUCHI Y, JIAN Y D, RAMALINGAM S, et al. Point-plane SLAM for hand-held 3D sensors[C]//2013 IEEE International Conference on Robotics and Automation. IEEE, 2013: 5182-5189.
|
| [8] |
FERNÁNDEZ-MORAL E, RIVES P, ARÉVALO V, et al. Scene structure registration for localization and mapping[J]. Robotics and Autonomous Systems, 2016, 75: 649-660. DOI:10.1016/j.robot.2015.09.009 |
| [9] |
SALAS-MORENO R F, GLOCKEN B, KELLY P H J, et al. Dense planar SLAM[C]//2014 IEEE International Symposium on Mixed and Augmented Reality (ISMAR). IEEE, 2014: 157-164.
|
| [10] |
HSIAO M, WESTMAN E, ZHANG G, ET AL. Keyframe-based dense planar SLAM[C]//2017 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2017: 5110-5117.
|
| [11] |
MA L, KERL C, STÜCKLER J, et al. CPA-SLAM: Consistent plane-model alignment for direct RGB-D SLAM[C]//2016 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2016: 1285-1291.
|
| [12] |
CHO H G, YEON S, CHOI H, et al. Detection and compensation of degeneracy cases for IMU-kinect integrated continuous SLAM with plane features[J]. Sensors, 2018, 18(4): 935. DOI:10.3390/s18040935 |
| [13] |
COUGHLAN J M, YUILLE A L. Manhattan world: Compass direction from a single image by bayesian inference[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision. IEEE, 1999, 2: 941-947.
|
| [14] |
SCHINDLER G, DELLAERT F. Atlanta world: An expectation maximization framework for simultaneous lowlevel edge grouping and camera calibration in complex man-made environments[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'04). IEEE, 2004, 1: Ⅰ-Ⅰ.
|
| [15] |
STRAUB J, ROSMAN G, FREIFELD O, et al. A mixture of manhattan frames: Beyond the manhattan world[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2014: 3770-3777.
|
| [16] |
RUSU R B, Cousins S. 3D is here: Point Cloud Library (PCL)[C]//IEEE International Conference on Robotics & Automation. 2011: 1-4.
|
| [17] |
GRIMSON W E L, LOZANO-PEREZ T. Localizing overlapping parts by searching the interpretation tree[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(4): 469-482. |




