2. 安徽师范大学 数学与统计学院, 安徽 芜湖 241003
2. School of Mathematics and Statistics, Anhui Normal University, Wuhu Anhui 241003, China
非线性孤子波理论在地球物理、光学、力学、理论物理学等学科中有很重要的应用.例如在地理科学、海洋物理、散射波、燃烧理论等方面, 许多学者作了多方面的研究, 如Salathiel等利用Riccati方程映射方法研究了电晶格孤子行波[1], Yu等研究了Bose-Einstein冷凝体的孤子波[2], Chow等研究了
作者等人利用广义变分迭代、同伦映射、微分不等式和不动点理论等方法也研究了一些孤立波理论及有关的非线性问题[10-15].本文就是研究一类非线性高维扰动KG(Klein-Gordon)方程.对于一般较典型的KG方程已有许多研究, 它代表的是许多自然现象的简化情形.但此类方程已经不完全能满足当前科学发展的要求, 所以需要研究更能反映自然现象的广义非线性高维强迫扰动KG方程.
1 非线性高维扰动KG方程考虑如下广义非线性扰动KG方程:
| $ \begin{aligned} u_{tt} -a\, (u_{xx} +u_{yy} +u_{zz} )-mu+ku^3=f(u, u_z ), \end{aligned} $ | (1) |
其中
近年来, 关于非线性KG方程解的研究大体集中在两个方面.一方面是利用分析方法求出各种方程的精确解, 如He等[16]利用推广的
首先作行波变换:
| $ \begin{aligned} w=c_1 x+c_2 y+c_3 z+b\, t, \end{aligned} $ | (2) |
其中
| $ \begin{aligned} a\, (b^2-c_1^2 -c_2^2 -c_3^2 )u_{ww} -mu+ku^3=f(u, u_w ). \end{aligned} $ | (3) |
先考虑方程(3)当
| $ \begin{aligned} a\, (b^2-c_1^2 -c_2^2 -c_3^2 )u_{ww} -mu+ku^3=0. \end{aligned} $ | (4) |
我们用双曲函数待定系数的方法来求无扰动方程(4)的孤子波解.
设方程(4)有如下形式的解:
| $ \begin{aligned} v =C \tanh (dw)+C_2 \tanh ^2(dw), \end{aligned} $ | (5) |
这时
| $ \begin{aligned} v_{w} =d(1-\tanh ^2(dw))\, (C_1 +2C_2 \tanh (dw)), \end{aligned} $ | (6) |
| $ \begin{aligned} v_{ww} =2d^2(1-\tanh ^2(dw))[C_2 -C_1 \tanh (dw)\, -3C_2 \tanh ^2(dw)]. \end{aligned} $ | (7) |
将式(5)—(7)代入方程(4)中, 合并关于
| $ \begin{aligned} C_1 =\sqrt {\frac{m}{k}} , \quad C_2 =0, \quad d=\frac{a\, (c_1^2 +c_2^2 +c_3^2 )\pm \sqrt {a^2(c_1^2 +c_2^2 +c_3^2 )^2-4m} }{2}. \end{aligned} $ | (8) |
将式(8)的结果代入式(5), 得到方程(4)的两个孤子波解:
| $ \begin{aligned} v_1 (w)=\sqrt {\frac{m}{k}} \tanh \Big(\frac{a\, (c_1^2 +c_2^2 +c_3^2 )+\sqrt {a^2(c_1^2 +c_2^2 +c_3^2 )^2-4m} }{2}w \Big), \end{aligned} $ | (9) |
| $ \begin{aligned} v_2 (w)=\sqrt {\frac{m}{k}} \tanh \Big(\frac{a\, (c_1^2 +c_2^2 +c_3^2 )-\sqrt {a^2(c_1^2 +c_2^2 +c_3^2 )^2-4m} }{2}w \Big). \end{aligned} $ | (10) |
将变换式(2)代入式(9)、(10), 得到无扰动KG方程(4)的两个孤子波行波解:
| $ \begin{aligned} v_1 =\sqrt {\frac{m}{k}} \tanh \Big(\frac{a\, (c_1^2 +c_2^2 +c_3^2 )+\sqrt {a^2(c_1^2 +c_2^2 +c_3^2 )^2-4m} }{2}(c_1 x+c_2 y+c_3 z+b\, t)\Big), \end{aligned} $ | (11) |
| $ \begin{aligned} v_2 =\sqrt {\frac{m}{k}} \tanh \Big(\frac{a\, (c_1^2 +c_2^2 +c_3^2 )-\sqrt {a^2(c_1^2 +c_2^2 +c_3^2 )^2-4m} }{2}(c_1 x+c_2 y+c_3 z+b\, t)\Big). \end{aligned} $ | (12) |
注 我们可以根据非线性KG方程的具体物理过程的要求来选取上述得到的两个不同的孤子波作为下面求得孤子波摄动解的出发点.
取
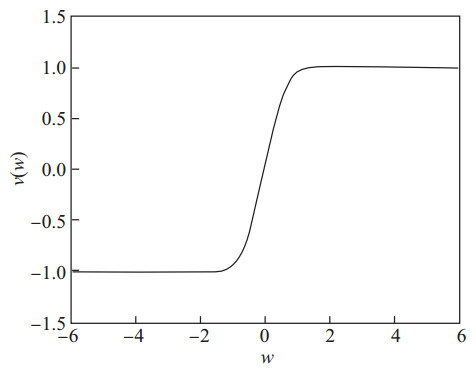
|
图 1 非线性方程(4)的孤子波曲线(11) Fig.1 The solitary waves curve (11) of nonlinear equation (4) |
不失一般性, 上述所列出的孤子波行波解(11)、(12), 在泛函变分迭代方法下, 都可作为扰动KG方程的泛函迭代式的初始近似.本文是利用式(9)作为初始近似, 即
为了求得非线性强迫扰动KG方程(3)具有较好精度的近似解, 现采用泛函分析变分迭代方法[16].作泛函
| $ \begin{equation} \label{eq13} F[u]=u-\int_{\;0}^{\;w} {\lambda (\xi )} [a\,(b^2-c_1^2 -c_2^2 -c_3^2 )u_{\xi \xi } -mu+k\overline {u}^3-\overline {f}(\overline {u},\overline {u}_w )]\mathrm d\xi , \end{equation} $ | (13) |
这里
计算式(13)的变分
| $ \begin{aligned} \delta \, F=\, &\delta \, u-a\, (b^2-c_1^2 -c_2^2 -c_3^2 )[\lambda (\xi )\delta \, u_\xi ]_{\xi =w}\notag\\ &+\int_{\;0}^{\, w} {\left[ {a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\frac{\mathrm d\lambda }{\mathrm d\xi }\cdot\frac{\mathrm d\, u}{\mathrm d\xi }-m\lambda } \right]} \, \delta u\mathrm d\xi\notag\\ =\, &\delta \, u-a\, (b^2-c_1^2 -c_2^2 -c_3^2 )[\lambda (\xi )\delta \, u_\xi ]_{\xi =w} \notag\\ &+a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\left[ {\frac{\mathrm d\lambda }{\mathrm d\xi }u} \right]_{\xi =w} \notag\\ &-\int_{\;0}^{\, w} {\left[ {a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\frac{\mathrm d^2\lambda }{\mathrm d\xi ^2}+m^2\lambda } \right]} \, \delta \, u\, \mathrm d\xi . \end{aligned} $ |
可得
| $ \begin{align} \delta \, F=\, &\delta {\kern 1pt}u+\left( {-\int_{\;0}^{\, w} {\left[ {a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\frac{\mathrm d^2\lambda }{\mathrm d\xi ^2}+m^2\lambda } \right]} \, \delta \, u\, \mathrm d\xi } \right)(\lambda \delta u_\xi ) \left| {_{\xi =w} } \right.\notag\\ &-\left(-\int_{\;0}^{\, w} {\left[ {a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\frac{\mathrm d^2\lambda }{\mathrm d\xi ^2}+m^2\lambda } \right]\, } \delta u\mathrm d\xi \right)(\lambda _\xi \delta u)\left| {_{\xi =w} } \right. \notag\\ &+\int_{\;0}^{\;z} {[a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\lambda _{\xi \xi } +m^2\lambda ]\delta u\mathrm d\xi } . \end{align} $ | (14) |
令泛函
| $ \begin{aligned} &\delta u-a\, (b^2-c_1^2 -c_2^2 -c_3^2 )(\lambda _\xi\delta u)\left| {_{\xi =w} } \right.=0, \\ &a\, (b^2-c_1^2 -c_2^2 -c_3^2 )(\lambda \delta u_\xi )\left| {_{\xi =w} } \right.=0, \\ &\int_{\;0}^{\;w} {[a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\lambda _{\xi \xi } +m\lambda ]\delta u\mathrm d\xi } =0. \end{aligned} $ |
于是由上述诸式可取对应的变分函数
| $ \begin{aligned} a\, (b^2-c_1^2 -c_2^2 -c_3^2 )\frac{\mathrm d^2\lambda }{\mathrm d\xi ^2}+m\lambda =0, \end{aligned} $ |
及对应的初始条件:
| $ \begin{aligned} \lambda (\xi )\left| {_{\xi =w} } \right.=0, \quad \frac{\mbox{d}\lambda }{\mathrm dw}\Big|_{\, \xi =w} =\frac{1}{a\, (b^2-c_1^2 -c_2^2 -c_3^2 )} . \end{aligned} $ |
于是可得
| $ \begin{aligned} \lambda (\xi )=-\sqrt {\frac{a\, (b^2-c_1^2 -c_2^2 -c_3^2 )}{m}} \sin \;\left( {\frac{\sqrt m }{\sqrt {a (b^2-c_1^2 -c_2^2 -c_3^2 )} }(w-\xi )} \right). \end{aligned} $ | (15) |
由式(14)、(15), 构造强迫扰动KG方程(3)解的迭代表示式:
| $ \begin{align} u_{n+1} =\, &u_n +\sqrt {\frac{a\, (b^2-c_1^2 -c_2^2 -c_3^2 )}{m}} \notag\\ &\times \int_{\;0}^w {\sin \left( {\frac{\sqrt m }{\sqrt {a\, (b^2-c_1^2 -c_2^2 -c_3^2 )} }(w-\xi )} \right)\, } [a\, (b^2-c_1^2 -c_2^2 -c_3^2 )(u_{n})_{\xi \xi } \notag\\ &-mu_n +ku_n^3 -{\kern 1pt}f(u_n , b(u_{n}){_{\xi }} )]\mathrm d\xi , \quad n=0, 1, \cdots . \end{align} $ | (16) |
选取典型的非线性方程(4)的一个孤子波解式(9)作为扰动KG方程的泛函迭代式(16)的初始近似
| $ \begin{aligned} u_0 (w)=\sqrt {\frac{m}{k}} \tanh \Big(\frac{a\, (c_1^2 +c_2^2 +c_3^2 )+\sqrt {a^2(c_1^2 +c_2^2 +c_3^2 )^2-4m} }{2}w\Big). \end{aligned} $ | (17) |
将式(17)代入式(16), 得到非线性强迫扰动方程(3)的一次近似解
| $ \begin{align} u_1 (w)=\, &\sqrt {\frac{m}{k}} \tanh \Big(\frac{a\, (c_1^2 +c_2^2 +c_3^2 )+\sqrt {a^2(c_1^2 +c_2^2 +c_3^2 )^2-4m} }{2}w\Big) \notag\\ &-\sqrt {\frac{a\, (b^2-c_1^2 -c_2^2 -c_3^2 )}{m}} \notag\\ &\times \int_{\;0}^w {\sin \, \left( {\frac{\sqrt m }{\sqrt {a\, (b^2-c_1^2 -c_2^2 -c_3^2 )} }(w-\xi )} \right)} [a\, (b^2-c_1^2 -c_2^2 -c_3^2 )(u_{0}){_{\xi \xi }} \notag\\ &-mu_n +ku_0^3 -f(u_0 , b(u_{0}){_{\xi }} )]\mathrm d\xi , \end{align} $ | (18) |
其中
由式(16)—(18)等迭代关系式, 依次可得到
现利用微分方程Picard逐次逼近法来证明函数序列
事实上, 迭代式(16)可写为:
| $ \begin{aligned} u_{n+1} =\, &u_n +\sqrt {\frac{a\, (b^2-c_1^2 -c_2^2 -c_3^2 )}{m}} \; \\ &\times \int_{\;0}^{\;w} {\sin \left( {\frac{\sqrt m }{\sqrt {a\, (b^2-c_1^2 -c_2^2 -c_3^2 } )\;{\kern 1pt}}(w-\xi )} \right)} \\ &\times [L(u_n (\xi ))-ku_n^3 -\, f(u_n (\xi ), b(u_{n}){_{\xi }} )]\mathrm d\xi , \end{aligned} $ |
其中
| $ \begin{aligned} L(\, u(w))=a\, (c_1^2 +c_2^2 +c_3^2 -b^2)u_{ww} -mu_w . \end{aligned} $ |
由非线性强迫扰动KG方程(1)的假设和泛函分析变分原理及其Euler方程的变分原理极值理论, 若
| $ \begin{aligned} \left| {\;(L(w_1 )-kw_1^3 -\, f)-(L(w_2 )-kw_2^3 -\, f)\;} \right|\le K\left| {w_1 -w_2 } \right| \end{aligned} $ |
对于一切的
| $ \begin{aligned} \left| {u_j (w)-u_{j-1} (w)} \right|\le \frac{\sqrt {1-a^2} K}{\, j!\cdot m}W_0^j , \quad \left| w \right|\le W_0 , \;\, j=1, 2, \cdots , \end{aligned} $ |
其中
于是可得如下结论.
定理 在方程(1)中, 设
由式(16)知,
| $ \begin{aligned} u(w)=\mathop {\lim }\limits_{n\to \infty } u_n (w) \end{aligned} $ | (19) |
就是非线性强迫扰动KG方程(3)的精确解.而
将行波变换(2)代入式(19):
为方便起见, 在非线性强迫扰动KG方程(1)中取扰动项函数
| $ \begin{aligned} u_{tt} -2(u_{xx} +u_{yy} +u_{zz} )-u+u^3=\varepsilon \exp (-u), \quad 0<\varepsilon \ll 1. \end{aligned} $ | (20) |
在行波变换
| $ \begin{aligned} w=x+y+z+2t \end{aligned} $ | (21) |
下, 对应的非线性扰动方程(20)为:
| $ \begin{aligned} 4u_{ww} -u+u^3=\varepsilon \exp (-u), \quad 0<\varepsilon \ll1. \end{aligned} $ | (22) |
由式(17), 方程(22)的初始迭代
| $ \begin{aligned} u_0 (w)=\tanh \big ((3+2\sqrt 2 )w \big). \end{aligned} $ |
即强迫扰动方程(22)的孤子波微扰解
| $ \begin{aligned} u_{\rm 0app} (w)=\tanh \big((3+2\sqrt 2 )w\big). \end{aligned} $ | (23) |
由迭代式(16)和(18), 得到强迫扰动方程(22)的孤子波微扰解
| $ \begin{align} u_{1{\rm app}} (w)=\, &\tanh \big((3+2\sqrt 2 )w\big) \notag\\ &-\sqrt 2 \varepsilon \int_{\;0}^w {\sin \left[ {\frac{1}{\sqrt 2 }(w-\xi )} \right]{\kern 1pt}} \exp \big(-\tanh \big((3+2\sqrt 2 )\xi \big)\big){\kern 1pt}{\kern 1pt}\mathrm d\xi . \end{align} $ | (24) |
取
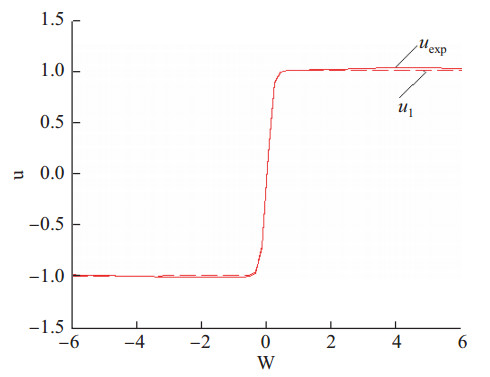
|
图 2 非线性KG方程(22)的孤子波扰动解的曲线 Fig.2 The curve of solitary waves disturbed solutions to the nonlinear KG equation (22) |
再将行波变换(21)代入式(24)式, 便得到强迫微扰KG方程(29)的一次近似孤子波微扰行波解
| $ \begin{aligned} u_{\rm 1app} (t, x, y, z)=\, &\tanh \big((3+2\sqrt 2 )(x+y+z+2t)\big) \\ &-\sqrt 2 \int_{\;0}^{x+y+z+2t} \sin \left[ {\frac{1}{\sqrt 2 }(x+y+z+2t-\xi )} \right]\exp \left[ {-\tanh \Big(\frac{3+2\sqrt 2 }{2}\xi \Big)} \right]\mathrm d\xi . \end{aligned} $ |
因非线性强迫扰动KG方程(20)是摄动方程, 利用摄动理论[23, 25]可以证明, 强迫微扰KG方程(22)的一次近似孤子波微扰行波解
| $ \begin{aligned} u_{\rm {exa}} (t, x, y, z)=u_{\rm 1app} (t, x, y, z)+O(\varepsilon ), \quad 0<\varepsilon \ll 1. \end{aligned} $ |
还可用相同的方法得到强迫微扰KG方程(20)的孤子波微扰解
本文选取的初始近似
由泛函变分迭代方法得到的非线性强迫扰动KG方程的孤子波近似解
| [1] |
SALATHIEL Y, AMADOU Y, GARMBO B G, et al. Soliton solutions and traveling wave solutions for a discrete electrical lattice with nonlinear dispersion through the generalized Riccati equation mapping method[J]. Nonlinear Dynamics, 2017, 87(4): 2435-2443. DOI:10.1007/s11071-016-3201-7 |
| [2] |
YU F J, LI L. Vector dark and bright soliton wave solutions and collisions for spin-1 Bose-Einstein condensate[J]. Nonlinear Dynamics, 2017, 87(4): 2697-2713. DOI:10.1007/s11071-016-3221-3 |
| [3] |
CHOW B, LU P. On к-noncollapsed complete noncompact shrinking gradient Ricci solitons which split at infinity[J]. Math Annalen, 2016, 366(3/4): 1195-1206. |
| [4] |
SAZONOV S V. New type of extremely short vector solitons in a medium of asymmetric molecules[J]. JETP Letters, 2015, 102(12): 834-840. DOI:10.1134/S0021364015240091 |
| [5] |
欧阳成, 姚静荪, 石兰芳, 等. 一类尘埃等离子体孤子波解[J]. 物理学报, 2014, 63(11): 110203-110208. DOI:10.7498/aps.63.110203 |
| [6] |
石兰芳, 朱敏, 周先春, 等. 一类非线性发展方程孤立子行波解[J]. 物理学报, 2014, 63(13): 130201-130205. DOI:10.7498/aps.63.130201 |
| [7] |
OUYANG C, CHENG L H, MO J Q. Solving a class of burning disturbed problem with shock layers[J]. Chin Phys B, 2012, 21(5): 15-18. |
| [8] |
SHI L F, CHEN C S, ZHOU X C. The extended auxiliary equation method for the KdV equation with variable coefficients[J]. Chin Phys B, 2011, 20(10): 803-811. |
| [9] |
石兰芳, 周先春. 一类扰动Burgers方程的孤子同伦映射解[J]. 物理学报, 2010, 59(5): 2915-2918. |
| [10] |
MO J Q. Homotopic mapping solving method for gain fluency of a laser pulse amplifier[J]. Science in China G, 2009, 39(7): 1007-1010. |
| [11] |
MO J Q, LIN S R. The homotopic mapping solution for the solitary wave for a generalized nonlinear evolution equation[J]. Chin Phys B, 2009, 18(9): 3628-3631. DOI:10.1088/1674-1056/18/9/004 |
| [12] |
MO J Q. Solution of travelling wave for nonlinear disturbed long-wave system[J]. Commun Theor Phys, 2011, 55(3): 387-390. DOI:10.1088/0253-6102/55/3/02 |
| [13] |
MO J Q, CHEN X F. Homotopic mapping method of solitary wave solutions for generalized complex Burgers equation[J]. Chin Phys B, 2010, 19(10): 20-23. |
| [14] |
XU J Z, ZHOU Z F. Existence and uniqueness of anti-periodic solutions for a kind of nonlinear nth-order differential equation with multiple deviating arguments[J]. Ann Diff Eqn, 2012, 28(1): 105-114. |
| [15] |
徐建中, 周宗福. 一类四阶具有多个偏差变元p-Laplacian中立型微分方程周期解的存在性[J]. 重庆工商大学学报, 2012, 29(11): 9-16. |
| [16] |
HE J H, WU X H. Construction of solitary solution and compaction-like solution by variational iteration method[J]. Chaos Solitons & Fractals, 2006, 29(1): 108-113. |
| [17] |
ZHANG X A, CHEN K, DUAN Z I. Bound states of KG equation and Dirac for ring-shaped non-spherical oscillator scalar and vector potential[J]. Chin Phys, 2005, 14(1): 42-44. DOI:10.1088/1009-1963/14/1/009 |
| [18] |
ZHANG Q, YUE P, GONG L X. New exact solutions of nonlinear KG equation[J]. Chin Phys, 2006, 15(1): 35-38. DOI:10.1088/1009-1963/15/1/006 |
| [19] |
TEMAN R. Infinite-dimensional Dynamical System in Mechanics and Physics[M]. 2nd ed. New York: Springer, 1997.
|
| [20] |
张建文, 王旦霞, 吴润衡. 一类广义强阻尼Sine-Gordon方程的整体解[J]. 物理学报, 2008, 57(4): 2021-2025. DOI:10.3321/j.issn:1000-3290.2008.04.006 |
| [21] |
韩兆秀. 非线性KG方程新的精确解[J]. 物理学报, 2005, 54(4): 1481-1484. DOI:10.3321/j.issn:1000-3290.2005.04.006 |
| [22] |
卢殿臣, 杨立波, 洪宝剑. 非线性KG方程新的精确解[J]. 江苏大学学报, 2010, 31(1): 120-124. DOI:10.3969/j.issn.1671-7775.2010.01.025 |
| [23] |
CHANG K W, HOWES F A. Nonlinear Singular Perturbation Phenomena:Theory and Applications[M]. New York: Springer-Verlag, 1984.
|
| [24] |
DE JAGER E M, JIANG F R. The Theory of Singular Perturbation[M]. Amsterdam: North-Holland Publishing Co, 1996.
|
| [25] |
BARBU L, MOROSANU G. Singularly Perturbed Boundary-Value Problems[M]. Basel: Birkhauser, 2007.
|




