特殊函数是指一些具有特定性质的函数, 它们广泛应用于物理学、化学、工程、统计学以及计算机科学等领域.大多数特殊函数都没有闭形式的表达式, 其赋值只能通过数值逼近来实现.由于特殊函数在应用中的重要性和广泛性, 因此, 如何提高数值逼近的效率, 具有重要的学术意义和应用价值.
有关特殊函数的性质和数值计算方法, 众多国内外学者作出了大量的研究. 1964年, Abramowitz、Stegun和Romain在文献[1]中详细介绍了特殊函数的定义、性质、数值逼近方法. 2010年, 美国国际标准与技术研究院(NIST)发布了NIST数学函数数字图书馆(Digital Library of Mathematical Functions, DLMF)[2], 系统地介绍了特殊函数的性质和常用赋值方法.
贝塞尔函数(Bessel functions)是德国数学家贝塞尔于1817年研究三体引力系统的运动问题时提出的.贝塞尔函数在波的传播、有势场和信号处理领域有着广泛的应用, 如圆柱形波导中的电磁波传播、调频合成等.
贝塞尔函数是一类特殊函数, 无法由初等函数直接表示.针对贝塞尔函数的数值逼近, 已有的研究提出了许多数值方法[1-2].文献[3]对整数阶和半整数阶第一类贝塞尔函数的幂级数、渐近级数和连分式展开进行了比较.文献[4]对任意整数阶的贝塞尔函数讨论了多项式逼近.文献[5]提出了基于泰勒级数展开、Debye渐近展开和Sommerfeld积分的算法, 对贝塞尔函数进行逼近.
在之前的工作中, 幂级数、渐近级数展开等数值方法对整数阶第一类贝塞尔函数的逼近效率不高, 且在数值上不稳定.我们注意到贝塞尔函数表现出近似周期性的性质.因此, 在本文中, 针对贝塞尔函数的这一性质, 考虑通过三角函数的和形式(
基于傅里叶级数的方法是基于这种思路的一种应用.傅里叶级数在理论、数学和工程领域都有着重要的研究价值.傅里叶级数方法是把类似波的函数表示成简单正弦波的和, 它把任何周期函数或周期信号分解成简单震荡函数(如正弦函数和余弦函数)的集合.在文献[6]中, 提出了利用傅里叶级数展开对贝塞尔函数进行逼近.然而, 正如本文实验所示, 形式为αicos(kx)和αisin(kx)的和的逼近效果并不理想.
我们转而考虑另一种三角函数形式的逼近方法. Prony方法作为傅里叶级数的一种拓展, 最早由Prony在1795年提出[7]. Prony方法通过在一个均匀采样的样本中提取有用的信息, 并建立一系列的衰减指数或正弦函数. Prony方法常作为一种线谱估计方法应用于各领域的信号处理.但Prony模型在数值上是病态的, 非最优、非严格的近似求解算法, 对噪音的干扰非常敏感, 这极大地限制了Prony模型的应用. Prony方法的复兴起源于对Prony方法的修改, 这显著稳定了原始方法, 例如, ESPRIT方法, 矩阵束方法或近似Prony方法[8-11].近年来, Prony方法也已经成功应用于不同的逆问题, 如, 量子化学[12]或流体动力学[13]中Green函数的近似, 反向散射中粒子的定位[14]等.
本文中, 我们针对整数阶第一类贝塞尔函数, 基于扩展形式的Prony方法, 采用三角函数和的形式对第一类贝塞尔函数进行逼近, 并将实验结果与基于傅里叶级数方法的实验结果作比较.
本文第1节介绍了第一类贝塞尔函数的定义和相关性质; 第2节介绍了贝塞尔函数的基于傅里叶级数展开形式; 第3节和第4节分别介绍了指数形式的Prony方法和三角函数形式的Prony-like方法; 第5节分别应用基于傅里叶级数方法和Prony-like方法对第一类贝塞尔函数进行数值逼近, 并比较两种方法的逼近效果.
本文中,
定义1 如下形式的二阶常微分方程:
| $ \begin{equation} x^{2}\frac{{\rm d}^2y}{{\rm d}x^2}+x\frac{{\rm d}y}{{\rm d}x}+(x^{2}-v^2)=0 \end{equation} $ | (1) |
称为贝塞尔方程, 其中,
贝塞尔方程(1)的解
| $ \begin{equation*} y(x)=c_1 {\rm J}_v (x)+c_2 {\rm Y}_v (x) \end{equation*} $ |
可以由两个独立的函数来表示, 其中,
| $ \begin{equation*} {\rm J}_v (x)=\sum\limits_{m=0}^\infty {\frac{(-1)^m}{m!\Gamma (v+m+1)}\Big(\frac{x}{2}\Big)^{2m+v}} \end{equation*} $ |
称为第一类贝塞尔函数(Bessel functions of the first kind),
| $ \begin{equation*} \mbox{Y}_v (x)=\frac{{\rm J}_v (x)\cos (vπ )-{\rm J}_{-v} (x)}{\sin (vπ )} \end{equation*} $ |
称为第二类贝塞尔函数(Bessel functions of the second kind),
由上式知, 第二类贝塞尔函数Yv (x)可由第一类贝塞尔函数Jv (x)表示, 从而可转化为对第一类贝塞尔函数的研究.
本文仅考虑整数阶第一类贝塞尔函数Jn (x), 其中
由文献[1]知, Jn (x)满足性质
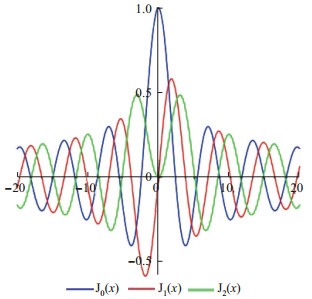
图 1分别给出了Jn (x)在n=0, 1, 2时的函数图象.
|
图 1 J0 (x), J1 (x)和J2 (x)的图象 Fig.1 Graphs of J0 (x), J1 (x) and J2 (x) |
本节中, 我们应用傅里叶级数展开对第一类贝塞尔函数进行研究.令b为正实数, 且
| $ {F_n}(b, t) = \left\{ \begin{array}{l} {{\rm{J}}_0}(b\sqrt {1 - {t^2}} ), n = 0, \\ \frac{{{{\rm{J}}_n}(b\sqrt {1 - {t^2}} )}}{{\sqrt {1 - {t^2}} }}, n \ge 1. \end{array} \right. $ |
由文献[6]可得
| $ \begin{equation} \label{eq2} F_n (b, t)=\frac{1}{2}\sum\limits_{k=-\infty }^\infty {f_n (b, k{\pi })} {\rm e}^{-{\rm i}k{\pi }t}, \quad t\in [-1, 1], \quad n\ge 0, \end{equation} $ | (2) |
其中, i为虚数单位,
| $ {f_n}(b, s) = \left\{ \begin{array}{l} \sqrt 2 {({b^2} + {s^2})^{ - \frac{1}{4}}}{{\rm{J}}_{\frac{1}{2}}}(\sqrt {{b^2} + {s^2}} ), n = 0, \\ {\rm{\pi }}{{\rm{J}}_{\frac{n}{2}}}(\frac{{\sqrt {{b^2} + {s^2}} - s}}{2}){{\rm{J}}_{\frac{n}{2}}}(\frac{{\sqrt {{b^2} + {s^2}} + s}}{2}), n \ge 1. \end{array} \right. $ |
作变量替换
| $ {J_n}(y;b): = \left\{ \begin{array}{l} {{\rm{J}}_0}(b\sqrt {1 - {t^2}} ) = {{\rm{J}}_0}(y), \;\;n = 0, \\ \frac{{{{\rm{J}}_n}(b\sqrt {1 - {t^2}} )}}{{\sqrt {1 - {t^2}} }} = \frac{{{{\rm{J}}_n}(y)}}{{\frac{y}{b}}}, \;\;n \ge 1. \end{array} \right. $ |
由t∈ [-1, 1]得y∈ [0, b].因此, 从式(2)可得
| $ \begin{equation} \label{eq3} J_0 (y;b):={\rm J}_0 (y) =\sum\limits_{k=0}^\infty {\varepsilon _k f_0 } (b, k\pi )\cos \Big( {k\pi \sqrt {1-\frac{y^2}{b^2}} } \Big), \quad y\in [0, b], \end{equation} $ | (3) |
| $ \begin{equation} \label{eq4} J_n (y;b):=\frac{{\rm J}_n (y)}{\frac{y}{b}}=\sum\limits_{k=0}^\infty {\varepsilon _k } f_n (b, k\pi )\cos \Big( {k\pi \sqrt {1-\frac{y^2}{b^2}} } \Big), n\ge 1, y\in [0, b], \end{equation} $ | (4) |
其中
| $ \varepsilon k=\left\{ \begin{array}{l} \frac{1}{2}, \;\;\;当k = 0, \\ 1, \;\;\;当k > 0, \end{array} \right. $ |
即, 将
图 2分别给出了变量替换后的函数

|
图 2 J0(y; b)、J1(y; b)和J2(y; b)的图像 Fig.2 Graphs of J0(y; b), J1(y; b)and J2(y; b) |
本节中, 我们介绍一种指数逼近的Prony方法. Prony方法可应用于计算一元函数的指数逼近, 即对于给定的函数
| $ \begin{align*} f(x)\approx \alpha _1 {\rm e}^{\varphi _1 x}+\alpha _2 {\rm e}^{\varphi _2 x}+\cdots +\alpha _m {\rm e}^{\varphi _m x}, \quad \alpha _i , \varphi _i \in {\mathbb{C}}. \end{align*} $ |
给定
问题1 求解线性方程组
| $ \left\{ \begin{array}{l} {f_{m - 1}}{c_1} + {f_{m - 2}}{c_2} + \cdots + {f_0}{c_m} = {f_m}, \\ {f_m}{c_1} + {f_{m - 1}}{c_2} + \cdots + {f_1}{c_m} = {f_{m + 1}}, \\ \cdots \cdots \\ {f_{M - 2}}{c_1} + {f_{M - 3}}{c_2} + \cdots + {f_{M - m - 1}}{c_m} = {f_{M - 1}}, \end{array} \right. $ |
以得到
问题2 求多项式
| $ (\mu -\mu _1 )(\mu -\mu _2 )\cdots (\mu -\mu _m ) = \mu ^m-c_1 \mu ^{m-1}-c_2 \mu ^{m-2}-\cdots -c_{m-1} \mu -c_m . $ |
问题3 求解线性方程组
| $\left\{ \begin{array}{l} {\alpha _1} + {\alpha _2} + \cdots + {\alpha _m} = {f_0}, \\ {\alpha _1}{\mu _1} + {\alpha _2}{\mu _2} + \cdots + {\alpha _m}{\mu _m} = {f_1}, \\ {\alpha _1}\mu _1^2 + {\alpha _2}\mu _2^2 + \cdots + {\alpha _m}\mu _m^2 = {f_2}, \\ \cdots \cdots \\ {\alpha _1}\mu _1^{M - 1} + {\alpha _2}\mu _2^{M - 1} + \cdots + {\alpha _M}\mu _M^{M - 1} = {f_{M - 1}}, \end{array} \right. $ |
其中
然而, 上述Prony方法中的多项式求根问题在数值上是病态的, 非最优、非严格的近似求解算法对噪音的干扰非常敏感, 这极大地限制了Prony方法的应用. 1999年, Golub等提出Prony方法的一种重要表述, 将求解Hankel系统和求解生成多项式的根的问题转化为求解一个广义特征值问题[15].广义特征值问题一般可通过Cholesky分解和LU分解来有效求解, 存在成熟的且数值稳定的数值方法, 因此, 这一新表示使Prony方法的应用得以\linebreak复兴.
下面, 我们来简单介绍一下基于广义特征值问题表述的Prony方法.
给定正实数
| $ \begin{align} f(x)\approx \sum\limits_{i = 1}^m {\alpha _i } {\rm e}^{\varphi _i x}, \quad \alpha_i, \phi_i\in\mathbb{C}. \end{align} $ | (5) |
展开式(5)的具体计算步骤如下.
(i) 给定展开项数
| $ \begin{align*} &x_j = a+j\Delta , \quad j = 0, 1, 2, \cdots, {2}m-1, \quad \Delta = \frac{b-a}{2m-1}, \\ &f_j = f(x_j ), \quad j = 0, 1, 2, \cdots, {2}m-1. \end{align*} $ |
(ii) 构造
| $ \begin{align*} A_0 = \left( {{\begin{array}{*{20}c} {f_0 }& {f_1 } & \cdots & {f_{m-1} }\\ {f_1 } & {f_2 } & \cdots & {f_m } \\ \vdots & \vdots & & \vdots \\ {f_{m-1} } & {f_m } & \cdots & {f_{2m-2} }\\ \end{array} }} \right), A_1 = \left( {{\begin{array}{*{20}c} {f_1 } & {f_2 } & \cdots & {f_m } \\ {f_2 } & {f_3 } & \cdots & {f_{m+1} } \\ \vdots & \vdots & & \vdots \\ {f_m } & {f_{m+1} } & \cdots & {f_{2m-1} } \\ \end{array} }} \right). \end{align*} $ |
(iii) 求解广义特征值问题
| $ A_{1} \nu = \lambda _i A_{0} \nu , \quad i = 1, \cdots, m, $ |
以计算
(iv) 求解如下线性方程组
| $ \begin{align*} \left( {{\begin{array}{*{20}c} 1 &\cdots&1\\ \lambda _1&\cdots& \lambda _m \\ \vdots&& \vdots \\ \lambda _1 ^{m-1}&\cdots&\lambda _m ^{m-1} \\ \end{array} }} \right)\left( {{\begin{array}{*{20}c} {\alpha _1 } \\ \vdots \\ {\alpha _m } \\ \end{array} }} \right) = \left( {{\begin{array}{*{20}c} {f_0 } \\ {f_1 }\\ \vdots\\ {f_{m-1} }\\ \end{array} }} \right), \end{align*} $ |
以计算系数
(v) 令
| $ f(x) = \sum\limits_{i = 1}^m {\alpha _i } {\rm e}^{\varphi _i x} $ |
为所求的逼近式.
Prony方法可以把求解
注 由于我们得到了函数的
| $ \begin{align*} \left( {{\begin{array}{*{20}c} 1 & \cdots & 1\\ {\lambda _1 } & \cdots & {\lambda _m }\\ \vdots & & \vdots \\ {\lambda _1 ^{m-1}} & \cdots & {\lambda _m ^{m-1}} \\ {\lambda _1 ^m} & \cdots & {\lambda _m ^m}\\ \vdots & \cdots& \vdots \\ {\lambda _1 ^{2m-1}} & \cdots & {\lambda _m ^{2m-1}}\\ \end{array} }} \right)\left( {{\begin{array}{*{20}c} {\alpha _1 } \\ \vdots \\ {\alpha _m }\\ \end{array} }} \right) = \left( {{\begin{array}{*{20}c} {f_0 } \\ {f_1 } \\ \vdots \\ {f_{m-1} }\\ {f_m } \\ \vdots \\ {f_{2m-1} }\\ \end{array} }} \right) \end{align*} $ |
来取得.但超定方程组一般没有精确解, 尽管可以通过最小二乘法来求近似解.为了尽量提高逼近效果, 我们只采用
由欧拉公式
本节中, 我们对Prony方法进行扩展, 分别考虑cosine形式和sine形式的Prony-like方法.
4.1 cosine形式的Prony-like方法给定正实数
| $ \begin{equation} f(x)\approx \sum\limits_{i = 1}^m {\alpha _i \cos } ( {\varphi _i x} ), \quad m\in {\mathbb{Z}}^+, \quad\alpha _i , \varphi _i \in {\mathbb{C}}. \end{equation} $ | (6) |
下面介绍具体步骤.
(i) 给定展开项数
| $ x_j = j\Delta , \quad j = 0, 1, \cdots , 2m-1, \quad \Delta = \frac{b}{2m-1}, $ |
| $ f_j = f(x_j ) = f(j\Delta ), \quad j = 0, 1, \cdots , 2m-1. $ |
(ii) 构造
| $ \begin{align*} A_0 = \left( {{\begin{array}{*{20}c} {2f_0 } & {2f_1 } & \cdots & {2f_{m-1} }\\ {2f_1 } & {f_2 +f_0 } & \cdots & {f_m +f_{m-2} }\\ \vdots & \vdots & & \vdots\\ {2f_{m-1} }& {f_m +f_{m-2} } & \cdots & {f_{2m-2} +f_0 }\\ \end{array} }} \right), \end{align*} $ |
| $ \begin{align*} A_1 = \left( {{\begin{array}{*{20}c} {2f_1 } & {f_2 +f_0 } & \cdots & {f_m +f_{m-2} } \\ {2f_2 } & {f_3 +f_1 } & \cdots & {f_{m+1} +f_{m-3} }\\ \vdots & \vdots & & \vdots\\ {2f_m } & {f_{m+1} +f_{m-1} } & \cdots \hfill & {f_{2m-1} +f_1 }\\ \end{array} }} \right), \end{align*} $ |
| $ \begin{align*} A_2 = \left( {{\begin{array}{*{20}c} {2f_1 }& {f_2 +f_0 } & \cdots & {f_m +f_{m-2} }\\ {2f_0 } & {2f_1 } & \cdots & {2f_{m+1} } \\ \vdots & \vdots && \vdots\\ {2f_{m-2} } & {f_{m-1} +f_{m-3} } & \cdots & {f_{2m-3} +f_1 } \\ \end{array} }} \right). \end{align*} $ |
(iii) 求解广义特征值问题
| $ \frac{1}{2}(A_1 +A_2 )\nu = \lambda _i A_0 \nu , \quad i = 1, 2, \cdots , m, $ |
以计算
(iv) 求解如下的线性方程组以计算系数
| $ \begin{align*} \left( \!\!\!{{\begin{array}{cccc} 1 &1&\cdots& 1 \\ {\cos (\arccos (\lambda _1 ))} & \cos (\arccos (\lambda _2 ))& \cdots & {\cos (\arccos (\lambda _m ))} \\ {\cos (2\arccos (\lambda _1 ))} &\cos (2\arccos (\lambda _2 ))& \cdots & {\cos (2\arccos (\lambda _m ))} \\ \vdots &\vdots&& \vdots \\ {\cos ((m-1)\arccos (\lambda _1 ))} &\cos((m-1)\arccos (\lambda_2)) &\cdots& {\cos ((m-1)\arccos (\lambda _m ))}\\ \end{array} }} \!\!\right) \left( \!\!\!{{\begin{array}{*{20}c} {\alpha _1 } \\ {\alpha _2 }\\ \vdots \\ {\alpha _m } \\ \end{array} }}\!\!\!\right) = \left(\!\!\! {{\begin{array}{*{20}c} {f_0 } \\ {f_1 } \\ \vdots \\ {f_{m-1} } \\ \end{array} }} \!\!\!\right). \end{align*} $ |
(v) 令
| $ \begin{align*} f(x) = \sum\limits_{i = 1}^m {\alpha _i \cos ( {\varphi _i x} )} \end{align*} $ |
为所求的逼近式.
4.2 sine形式的Prony-like方法类似4.1节, 我们将介绍另一种sine版本的Prony-like方法[17].
给定正实数
| $ \begin{equation} f(x)\approx \sum\limits_{i = 1}^m {\alpha _i \sin } ( {\varphi _i x} ), \quad m\in {\mathbb{Z}}^+, \quad\alpha _i , \varphi _i \in {\mathbb{C}}. \end{equation} $ | (7) |
具体步骤如下.
(i) 给定展开项数
| $ \begin{align*} x_j = j\Delta , \quad j = 0, \cdots , 2m, \quad \Delta = \frac{b}{2m}, \end{align*} $ |
| $ \begin{align*} f_j = -f(x_{-j} ), \quad j = 1-m, \cdots , -1, \quad f_0 = 0, \quad f_j = f(x_j ), \quad j = 1, \cdots , 2m. \end{align*} $ |
(ii) 构造如下
| $ \begin{align*} A = \left( {{\begin{array}{*{20}c} {2f_1 } & {f_2 +f_0 } & \cdots \hfill & {f_m +f_{2-m} } \\ {2f_2 } & {f_3 +f_1 } & \cdots & {f_{m+1} +f_{3-m} } \\ \vdots & \vdots & & \vdots \\ {2f_m }& {f_{m+1} +f_{m-1} } & \cdots & {f_{2m-1} +f_1 } \\ \end{array} }} \right), \end{align*} $ |
| $ \begin{align*} A_1 = \left( {{\begin{array}{*{20}c} {f_2 +f_0 } & {f_1 +\frac{f_3 +f_{-1} }{2}} & \cdots & {\frac{f_{m-1} +f_{3-m} +f_{m+1} +f_{1-m} }{2}} \\ {f_3 +f_1 } & {f_2 +\frac{f_4 +f_0 }{2}} & \cdots& {\frac{f_m +f_{4-m} +f_{m+2} +f_{2-m} }{2}} \\ \vdots & \vdots & & \vdots\\ {f_{m+1} +f_{m-1} } & {f_m +\frac{f_{m+2} +f_{m-2} }{2}} & \cdots & {\frac{f_{2m-2} +f_2 +f_{2m} +f_0 }{2}} \\ \end{array} }} \right). \end{align*} $ |
(iii) 求解广义特征值问题
| $ \begin{align*} A_1 \nu = \lambda _i A\nu , \quad i = 1, 2, \cdots , m, \end{align*} $ |
以计算
(iv) 求解如下的线性方程组以计算系数
| $ \begin{align*} \left( {{\begin{array}{*{20}c} {\sin (\arccos (\lambda _1 ))} & {\sin (\arccos (\lambda _2))}&\cdots & {\sin (\arccos (\lambda _m ))} \\ {\sin (2\arccos (\lambda _1 ))} &{\sin (2\arccos (\lambda _2))}& \cdots & {\sin (2\arccos (\lambda _m )} \\ \vdots & \vdots&& \vdots \\ {\sin (m\arccos (\lambda _1 ))} &{\sin (m\arccos (\lambda _2 ))} & \cdots \hfill & {\sin (m\arccos (\lambda _m ))} \\ \end{array} }} \right)\left( {{\begin{array}{*{20}c} {\alpha _1 } \\ \alpha _2\\ \vdots \\ {\alpha _m } \\ \end{array} }} \right) = \left( {{\begin{array}{*{20}c} {f_1 } \\ {f_2 } \\ \vdots\\ {f_m } \\ \end{array} }} \right). \end{align*} $ |
(v) 令
| $ \begin{align*} f(x) = \sum\limits_{i = 1}^m {\alpha _i \sin ( {\varphi _i x})} \end{align*} $ |
为所求的逼近式.
用上面两种形式的Prony-like方法对函数
例1 我们给出cosine形式的Prony-like方法在
| $ \begin{align*} J_0 (y;1)\approx \, &0.200088133\cos ( {0.9876771383\; y} )+0.2000544332\cos ( 0.8909214296\; y)\\ &+0.199999955\cos ( {0.7069430127\; y})+0.1999455393\cos ( {0.4538236092y}) \\ &+0.199911938\cos ( {0.1563638168\; y}). \end{align*} $ |
在区间
在本节中, 我们用基于傅里叶级数的方法和Prony-like方法对
由
| $ \begin{align*} J_0 (y;b) = {\mathrm J}_0 (y), \quad J_1 (y;b) = \frac{{\mathrm J}_1 (y)}{\frac{y}{b}} \end{align*} $ |
知,
(1)
在
表 1展示了
|
表 1 Prony-like方法和基于傅里叶级数逼近 |
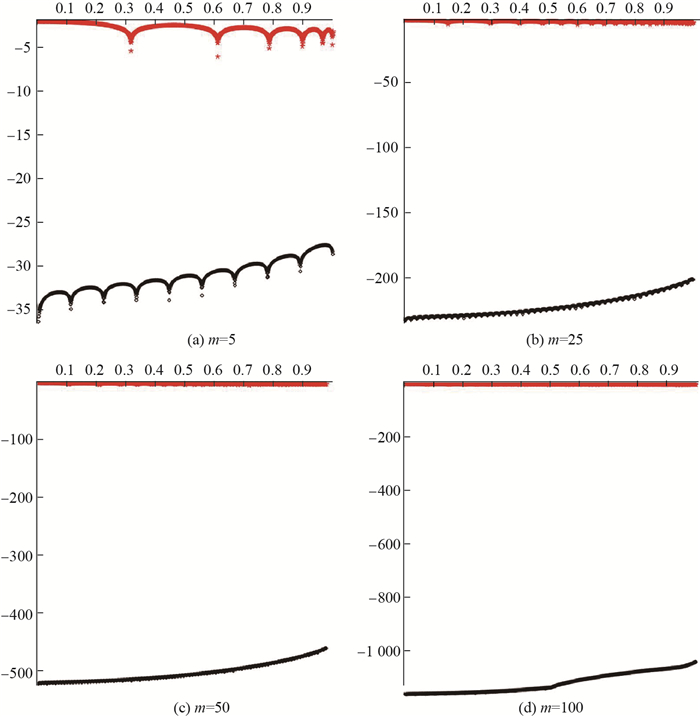
图 3分别展示了
|
图 3 Prony-like方法和基于傅里叶级数的函数 |
设
表 2和表 3分别展示了
|
表 2 Prony-like方法和基于傅里叶级数逼近 |
| 表 3 Prony-like方法和基于傅里叶级数逼近 ${J}_0(y;20)$ 的最大相对误差 Tab. 3 Maximal logarithmic relative error of $m$-th approximants of ${J}_0(y;20)$ via Fourier-based method and Prony-like method |
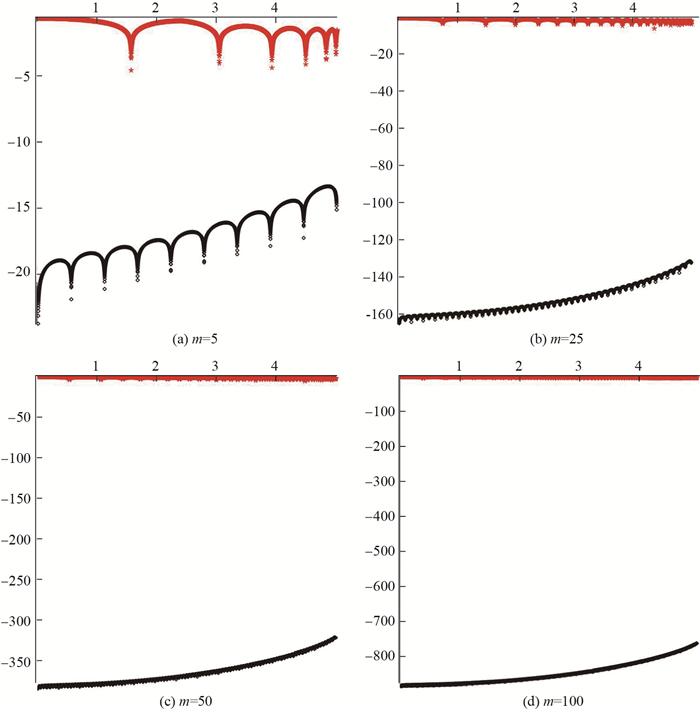
图 4展示了
|
图 4 Prony-like方法和基于傅里叶级数的函数 |
从表 1、表 2、表 3及图 3、图 4中可以看出, Prony-like方法的最大相对误差远小于基于傅里叶级数的方法, 且相对误差随展开项数的增大而效果更好.结合
(2)
在
表 4展示了
|
表 4 Prony-like方法和基于傅里叶级数逼近 |
图 5展示了
在
表 5、表 6展示了
图 6给出了在区间
从表 4、表 5、表 6及图 5、图 6中可以看出, 类似于
由于
令
表 7展示了
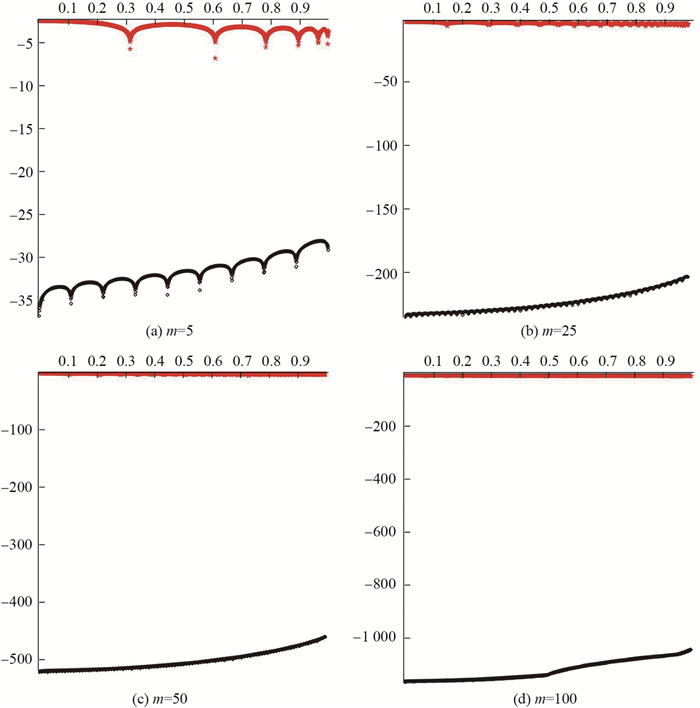
|
图 5 Prony-like方法和基于傅里叶级数的函数 |
|
表 5 Prony-like方法和基于傅里叶级数逼近 |
|
表 6 Prony-like方法和基于傅里叶级数逼近 |
图 7分别展示了
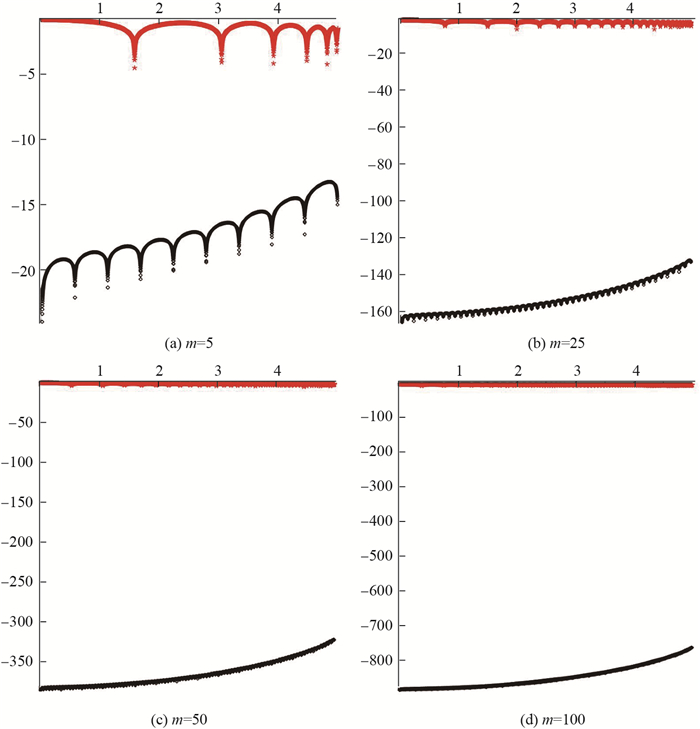
|
图 6 Prony-like方法和基于傅里叶级数的函数 |
|
表 7 Prony-like方法和基于傅里叶级数逼近 |
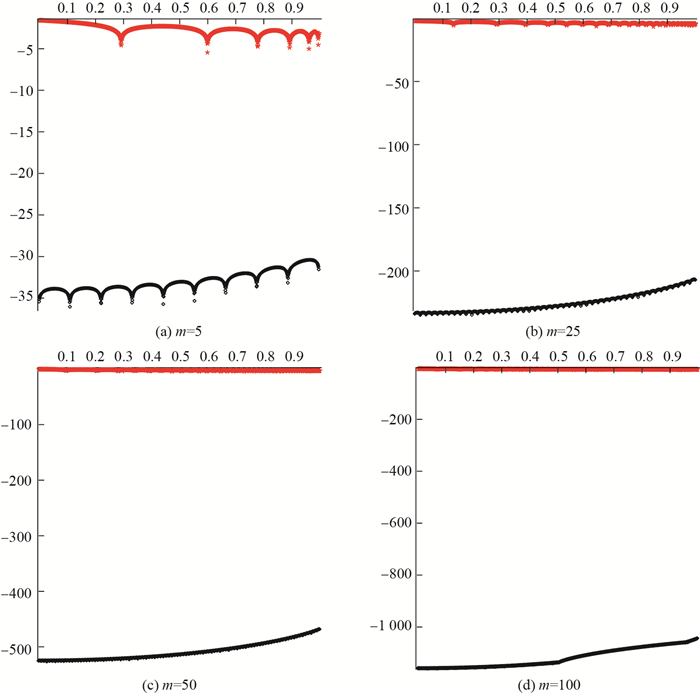
|
图 7 Prony-like方法和基于傅里叶级数的函数 |
以下, 设
表 8和表 9展示了
|
表 8 Prony-like方法和基于傅里叶级数逼近 |
|
表 9 Prony-like方法和基于傅里叶级数逼近 |
图 8展示了
从表 7、表 8、表 9及图 7、图 8中可以看出,
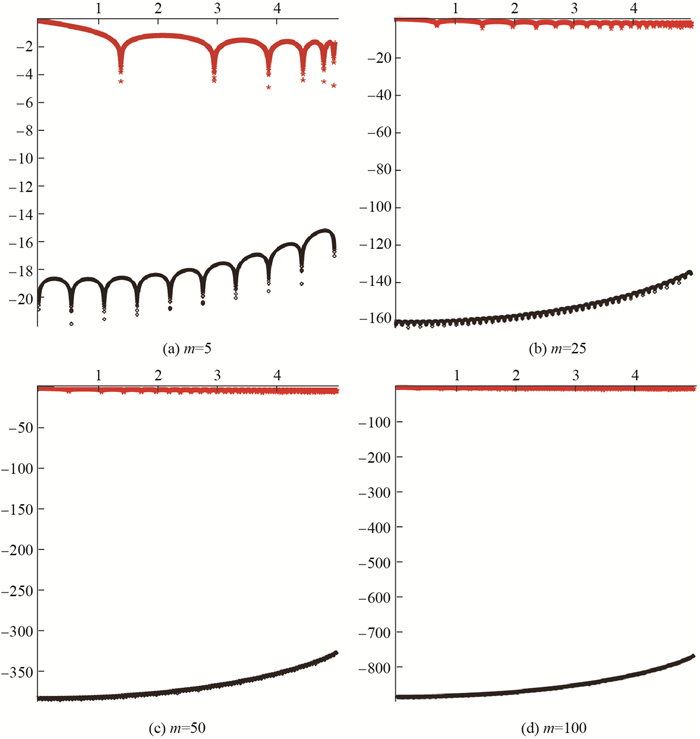
|
图 8 Prony-like方法和基于傅里叶级数的函数 |
本小节以函数
| 表 10 Prony-like方法和基于傅里叶级数的计算时间对比(时间单位: s) Tab. 10 Calculation times of Fourier-based method and Prony-like method |
从表 10可以看出, 基于傅里叶级数方法的计算时间比Prony-like方法的计算时间短, 且随着展开项数的增加, 两种方法计算时间的差距逐渐拉大.两种方法受自变量区间和阶数影响均不大.然而, Prony-like方法可以在项数很小时得到非常高的精度, 如
本文对整数阶第一类贝塞尔函数进行数值逼近.基于前面的分析和实验可得, cosine和sine形式Prony-like方法的数值逼近结果远远优于基于傅里叶级数方法, 虽然Prony-like方法的计\linebreak
算时间略长于基于傅里叶级数方法的计算时间, 但是Prony-like方法可以在项数很小时就得到很高的精度, 所以Prony-like方法的逼近效果更好.在未来的工作中, 将针对复数阶的贝塞尔函数应用Prony-like方法进行实验.作为Prony-like方法的改进, 下一步的研究将侧重于改进通过Hankel矩阵和广义特征值问题求解
| [1] |
ABRAMOWITZ M, STEGUN I A, ROMAIN J E. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables[M]. New York: Dover, 1964.
|
| [2] |
LOZIER D W. NIST Digital library of mathematical functions[J]. Annals of Mathematics & Artificial Intelligence, 2003, 38(1/3): 105-119. |
| [3] |
常晓阳.几类特殊函数的赋值分析研究[D].上海: 华东师范大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10269-1018821497.htm
|
| [4] |
MILLANE R P, EADS J L. Polynomial approximations to Bessel functions[J]. IEEE Transactions on Antennas & Propagation, 2003, 51(1): 1398-1400. |
| [5] |
MATVIYENKO G. On the evaluation of Bessel functions[J]. Applied and Computational Harmonic Analysis, 1993, 1(1): 116-135. DOI:10.1006/acha.1993.1009 |
| [6] |
ANDRUSYK A. Infinite series representations for Bessel functions of the first kind of integer order[EB/OL].[2018-10-20]. https://arxiv.org/abs/1210.2109
|
| [7] |
HILDEBRAND F B. Introduction to Numerical Analysis[M]. New Delhi: Tata McGraw-Hill Publishing Company Limited, 1956.
|
| [8] |
BOßMANN F, PLONKA G, PETER T, et al. Sparse deconvolution methods for ultrasonic NDT[J]. Journal of Nondestructive Evaluation, 2012, 31(3): 225-244. DOI:10.1007/s10921-012-0138-8 |
| [9] |
ROY R, PAULRAJ A, KAILATH T. Estimation of signal parameters via rotational invariance techniquesESPRIT[C]//Proceedings of the SPIE. International Society for Optics and Photonics, 1986:94-101. https://academic.oup.com/imaiai
|
| [10] |
HUA Y, SARKAR T K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(5): 814-824. DOI:10.1109/29.56027 |
| [11] |
POTTS D, TASCHE M. Nonlinear approximation by sums of nonincreasing exponentials[J]. Applicable Analysis, 2011, 90(3/4): 18. |
| [12] |
YANAI T, FANN G I, GAN Z, et al. Multiresolution quantum chemistry in multiwavelet bases:Analytic derivatives for Hartree-Fock and density functional theory[J]. Journal of Chemical Physics, 2004, 121(7): 2866-2876. DOI:10.1063/1.1768161 |
| [13] |
BEYLKIN G, CRAMER R, FANN G, et al. Multiresolution separated representations of singular and weakly singular operators[J]. Applied & Computational Harmonic Analysis, 2007, 23(2): 235-253. |
| [14] |
HANKE M. One shot inverse scattering via rational approximation[J]. Siam Journal on Imaging Sciences, 2012, 5(1): 465-482. DOI:10.1137/110823985 |
| [15] |
GOLUB G H, MILANFAR P, VARAH J. A Stable Numerical Method for Inverting Shape from Moments[M]. Society for Industrial and Applied Mathematics, 1999.
|
| [16] |
GIESBRECHT M, LABAHN G, LEE W S. Symbolic-numeric sparse polynomial interpolation in Chebyshev basis and trigonometric interpolation[C]//Proceedings of Computer Algebra in Scientific Computing (CASC 2004), 2004:195206.
|
| [17] |
CUYT A, LEE W S. Generalized eigenvalue relations:Spread polynomials and sine[R]. 2018.
|




