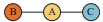2. 华东师范大学 计算中心, 上海 200062
2. Computer Center, East China Normal University, Shanghai 200062, China
图是用来表示数据的一种特殊数据结构, 它不仅可以用来表示实体本身的性质, 同时还可以用来表示实体之间的关系.图的这种特点使得图在多种领域具有广泛应用, 如生物信息学、网络分析等.随着社会和科学的发展, 实体之间的关系越来越多样, 实体的数量越来越多, 使用图结构来表示实体间的关系显得尤为高效, 从图数据中挖掘实用的模式亦显得越来越重要.
然而图结构虽然能高效地表示实体间的关系, 但其结构的复杂性使得从图中识别频繁的子图也变得困难.如在挖掘有用子图的过程中, 同构图的识别问题, 就被认为是一个NP(Non-deterministic Polynomia)完全问题.因此需要高效的频繁子图挖掘的方法.
现有的从图结构数据中挖掘频繁子图的方法主要分为两种:准确频繁图挖掘和近似频繁图挖掘.准确频繁图挖掘指从给定图或图数据库中挖掘频繁子图, 当记录每个子图的支持度时, 只计算与当前子图完全一致的同构图的数量, 如gSpan[1]和Grami[2]; 而近似频繁图挖掘与准确频图挖掘的主要区别为, 除了完全一致的同构图, 还同时记录与当前子图有一定区别的同构图的数量, 如gApprox[3]与AGraP[4].
由于获取数据的过程中, 不可避免数据丢失或噪音, 因此在实际应用中, 近似频繁子图挖掘更加符合用户需求.已有的近似频繁子图挖掘算法在计算两个给定图的近似程度时, 只关注其近似程度的绝对值, 即从一个图转化为另一个图需要的操作数的绝对值; 而在实际应用中, 在衡量两个图的近似程度时, 图本身的大小也是非常重要的衡量指标.
针对以上现有的近似频繁子图挖掘算法的问题, 本文提出了子图大小相关的近似频繁子图算法.该算法改进了子图近似程度的计算方式, 使得近似程度的结果与当前候选子图的大小有关.算法首先通过一个基于深度优先搜索策略的算法, 以及基于给定频繁程度和近似程度的子图大小上限算法, 生成所有符合大小要求的候选子图; 然后对每个候选子图生成一个最小的、需要搜索的近似子图集合, 并对其中的每个近似子图进行图同构搜索; 最后计算所有匹配的同构图中, 互斥的同构图的数量并将其作为子图的近似支持度.
本文算法的主要难点有: ①随着给定图的大小增加, 候选子图的数量呈指数增加, 因此需要一个有效的搜索方式及early-stop的条件; ②对任意一个候选子图, 其近似子图的数量随候选子图的大小呈指数式增加, 且由于图同构问题是一个NP完全问题, 因此高效的识别同构图十分困难; ③计算所有近似匹配中互斥匹配的数量, 及候选子图的近似支持度的问题, 可以转化为MIS(Maximum Independent Set)问题[5], 而MIS问题是一个公认的NP完全问题, 因此计算子图的近似支持度是一个重要且困难的问题.
基于以上算法的主要难点, 本文的主要贡献如下.
(1) 基于深度优先搜索策略的候选子图生成算法、候选子图大小上限的计算方法.
(2) 提出了一个基于点和边的删除尝试策略的近似子图生成算法、高效的图匹配算法.
(3) 根据近似频繁子图的特点, 利用候选子图的支持度上限, 来代替候选子图的准确支持度, 极大地提高了算法的效率.
(4) 实验证明, 与对比算法相比, 本文算法不仅高效, 同时能发现对比算法无法发现的近似频繁子图.
本文的结构如下:第1节介绍一些与本文提出算法及目标相关的工作; 第2节介绍一些相关概念; 第3节到第5节详细介绍本文算法的3大模块; 第6节通过实验展现本文算法的有效性; 第7节给出本文的总结与展望.
1 相关工作频繁子图挖掘指的是, 给定一个频繁程度下限, 从给定的图或图集合中挖掘出全部的、符合频繁程度要求的子图.因此频繁子图挖掘问题主要分为两种:单图中的频繁子图挖掘和图集合上的频繁子图挖掘.图集合上的频繁子图挖掘已经有许多成熟的工作, 如, gSpan算法[1], 在图集合中挖掘频繁子图, 避免了候选子图的生成; Gaston算法[6]修改了搜索策略, 从而使得算法速度加快.类似的算法还有gRed[7]和GraphSig[8].这些算法的不同及其优缺点在Cheng等的文章[9]和Krishna等的文章[10]中有详述的论述.
近年来, 随着数据规模的增大和需求的不断变化, 一些特殊的频繁子图挖掘算法也不断被提出.如, Choudhury等研究了在动态不断变化的图中挖掘可扩展的子图[11], 他们提出的算法可以随着给定图的变化, 动态地判定某个子图是否频繁; Ingalalli等研究了在多重图中的频繁子图挖掘[12], 其所提出的算法的目的是适应不断丰富且复杂化的数据, 除此之外, 该算法在应用于简单图上时, 也能取得良好的效果.
虽然单图中的频繁子图挖掘工作已经在多种应用中被提及, 如Alguliev等的工作[13]和Lima等的工作[14], 以及Elseidy等人提出的Grami算法[2], 都能有效地从单图中挖掘频繁子图.但对单图中的频繁子图挖掘的研究, 仍然少于图集合中的频繁子图挖掘的研究.研究表明, 单图中的频繁子图挖掘算法可以通过简单修改, 应用于图集合上; 然而图集合上的算法并不能应用于单图中[5].
近似频繁子图挖掘是在频繁子图挖掘的基础上, 当计算一个子图的支持度时, 除了与该子图完全一致的匹配, 同时计算满足一定近似程度的匹配.近似程度的计算通常有图的编辑距离[15]、结构区别[16]、特性区别[17]等几种方式.已经有一些近似频繁子图挖掘方面的工作, 如Holder等在SUBDUE上设计了一种变形函数[18], 使计算支持度时可以计算有一定区别的近似匹配; Chen等的gApprox在无标签的图上, 设计了函数计算图之间的编辑距离[18]; Jia等的APGM通过相容性矩阵计算图之间的距离, 从而允许子图的近似匹配与子图之间可以有点的区别[19]. AGraP[4]算法在此基础上进行了改进, 从而允许近似匹配与子图之间拥有点和边上的区别, 包括缺失和替换等. Flores-Garrido等在AGraP上进行了修改, 使算法挖掘全部近似频繁子图的子集CloseAFG[20].
除此之外, Acosta-Mendoza等研究了在多重图上的近似频繁子图挖掘[21], 并利用范式的思想, 使算法在时间成本和可扩展性上都有良好的效果.同时, Acosta-Mendoza等利用近似频繁子图挖掘算法, 设计了新的图像分类算法[22], 他们利用近似频繁子图挖掘算法的结果, 作为图像分类中图像的特征, 从而实现了在过程中自动计算和获取需求的替换矩阵, 并获得了令人满意的结果, 再次证明了近似频繁子图算法具有实际的意义.同时, Acosta-Mendoza等也对近似频繁子图挖掘算法的结果, 在图像聚类方面的应用做了研究[23], 并通过实验表明, 以近似频繁子图作为聚类的特征, 同样可以提升聚类的效果.
然而已有的近似频繁子图的挖掘算法, 在计算近似程度时, 只考虑了编辑距离的绝对值, 而忽略了图大小对近似程度的影响.因此, 本文提出了子图大小相关的近似程度计算方式, 并在此基础上设计了算法挖掘符合要求的近似频繁子图.
2 基本概念定义1 标签图 一个标签图
这是一个被广泛应用的定义, 图中的点表示实体, 边表示实体之间有一定关系, 点上的标签表示实体的属性或类别, 边上的标签表示的是实体之间关系的类别.如在蛋白质相互作用图(PPI: Protein-Protein Interaction)中, 点表示蛋白质, 点上的标签可以表示蛋白质种类.因此有许多点具有相同的标签, 边表示蛋白质之间可以发生相互作用, 边的标签表示相互作用的种类.
定义2 图同构 给定两个图
定义3 近似程度θ 给定一个图
| $ \begin{align} \theta =\frac{|g|-|g' |}{|g|}, \end{align} $ | (1) |
其中
定义4 近似匹配 给定两个图
如图 1所示, 给定图
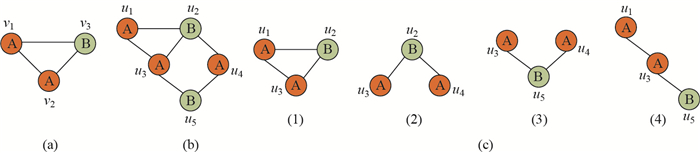
|
图 1 近似匹配例子 Fig.1 Example of approximate matches |
定义5 子图的近似支持度δ 给定图
通过以上定义, 可以对单图中的近似频繁子图挖掘问题给出形式化定义:给定单图
定义6 置信度ρ 给定图
例如图 1中图

|
图 2 图 |
本文算法的框架如图 3所示, 算法主要分为3个部分: ①第一部分遍历给定图的所有候选子图, 由于子图数量过多, 此处通过预测来确定可能的频繁子图的大小上限, 提高遍历速度. ②算法第二部分对每个子图生成所有的近似匹配, 由于当近似程度下限为1时, 寻找近似匹配的问题实际上是子图同构问题, 二子图同构问题被广泛认为是一个NP-complete的问题, 为了降低计算成本, 算法利用生成和搜索过程, 在生成阶段, 对候选子图的每个结点和边进行尝试删除, 生成所有符合近似要求, 且不互相包含的近似子图; 在搜索过程, 对每个近似子图进行查询. ③第三部分主要对子图的近似支持度进行计算.本文算法的原理和详细过程将在下面几节中详细阐述.
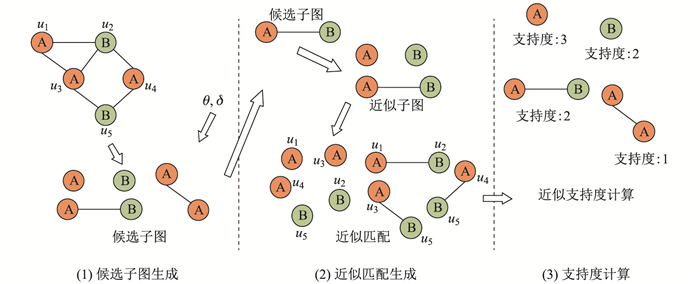
|
图 3 算法主要框架 Fig.3 Framework of our algorithm |
定理1 候选子图大小上限 对给定图
| $ \begin{align} |g|\leq \frac{|G|}{\theta\times\delta} \end{align} $ | (2) |
证明 由近似程度和近似匹配的定义可得, 子图
通过定理1, 本文设计了一个基于广度优先搜索的策略.具体策略步骤如下.
(1) 从当前图
(2) 从图
为了实现策略中的步骤(1), 本文设计了以下算法, 具体步骤如下.
(1) 如图 4所示, 从点1开始, 将点1标记为"必须的".
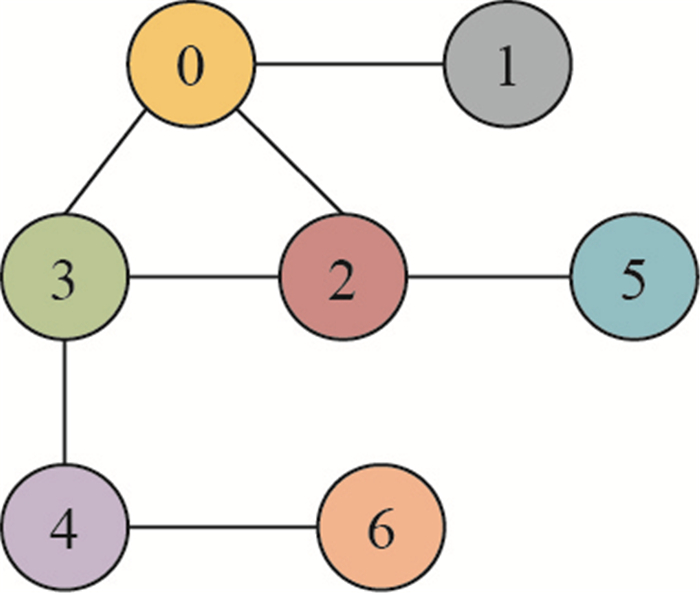
|
图 4 候选子图扩展例图 Fig.4 Example graph of candidate graph generation |
(2) 以当前子图为起点, 标记其所有邻居结点为被标记的, 如图 4中的点1, 2, 3.
(3) 使用邻居结点依次扩展当前子图, 获得的子图依次为01, 02, 03.
(4) 每获得一个新子图, 判断其大小是否超出候选子图大小上限.若不超出, 以当前子图为新起点, 重复步骤(2).
(5) 若获得的子图大小超出候选子图大小上限, 则终止当前扩展策略, 尝试扩展下一个被标记的邻居结点.
图 4中, 不考虑最小近似程度和支持度, 所有获得的子图按顺序应为: 0, 01, 012, 0123, 01234, 012345, 0123456, 012346, 01235, 0125
反单调性是提高挖掘效率的重要条件.在频繁图挖掘中, 反单调性是指, 给定图

|
图 5 反单调性无法保持示意图 Fig.5 Example when anti-monotonicity does not hold |
本文提出部分反单调性的概念, 定理如下.
定理2 局部反单调性 给定图
证明 当子图
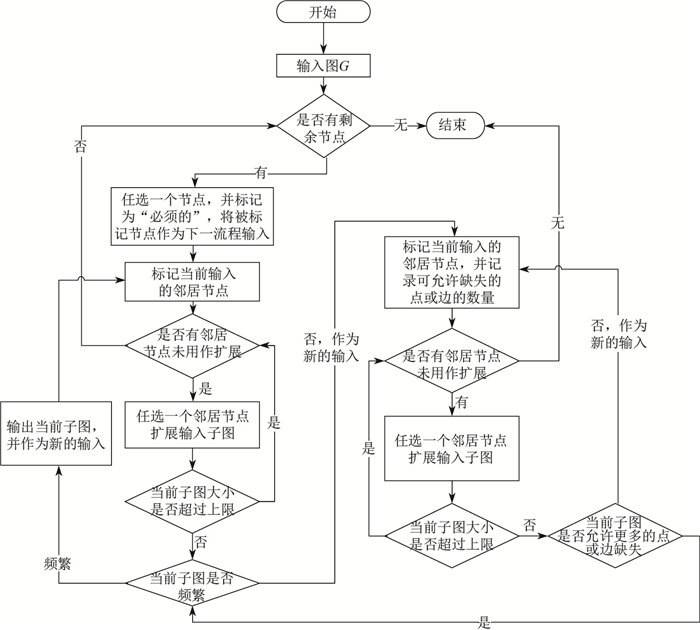
根据局部反单调性, 可以在前述算法上继续剪枝, 即在使用当前子图做新输入时, 若当前子图的支持度不符合最小支持度的要求, 则可以直接扩展当前子图, 而不需要判断其是否频繁, 直到可允许的点或边的数量发生改变.因此, 不需要对每个候选子图生成近似匹配和支持度的计算, 从而可以节省大量时间成本.同时, 由局部反单调性的证明可知, 当两个子图之间的关系符合局部反单调性的要求, 则其中较大的图的所有近似匹配, 必然是其子图的某个近似匹配的超图, 因此可以通过记录子图的所有近似匹配, 减少超图的近似匹配的搜索范围, 从而节省大量时间成本.改进后算法流程如图 6所示.
|
图 6 候选子图生成流程示意 Fig.6 Process of candidate subgraph generation |
定义7 近似子图 给定图
为了查询每个候选子图的近似支持度, 需要针对每个候选子图, 找出其在图中的所有近似匹配.为此提出了一个定理, 并在此基础上设计了一个基于点和边的删除的生成算法, 来找出候选子图的所有符合近似条件的子图.
定理3 给定图
证 明 任意
根据定理3, 可以确定对任意候选子图, 其最小需要进行匹配的近似子图集合中, 应不含两个图具有包含关系.
基于以上定理, 本文设计了一个基于点和边的删除的子图生成算法, 生成给定候选子图的所有符合近似条件的子图, 其基本思路如下, 具体算法见算法1.
| Algorithm 1 SimilarGraphGene |
| Input: |
| Output: All Similar Graph of g |
| 1: |
| 2:for each vertex or edge |
| 3: Deleted |
| 4: if |
| 5: Deleted |
| 6: end if |
| 7: |
| 8: if |
| 9: |
| 10: |
| 11: |
| 12: if |
| 13: SimilarGraphGene( |
| 14: if |
| 15: |
| 16: end if |
| 17: end if |
| 18: if |
| 19: |
| 20: end if |
| 21: end if |
| 22: undo line 3-5 |
| 23:end for |
| 24:return |
(1) 对所有点和边进行编号, 并按编号排序, 计算给定候选子图
(2) 遍历所有编号, 尝试删除编号对应的点或边, 并判断结果是否连通.若连通, 则将编号对应的点或边标记为已删除, 并更新当前已删除的点或边的数量.若不连通, 则跳过当前编号, 继续尝试.
(3) 以步骤(2)的结果为新的起点, 继续遍历剩余编号, 直至已删除的点或边的数量到达最大数量, 或剩余任意点或边的删除都会导致数量超出最大值, 则当前结果即为一个近似子图.
(4) 跳过最后一个被删除的点或边, 继续步骤(2), 直到所有点或边的组合删除都被尝试过.
步骤(3)的所有结果, 即为最终需要进行匹配的候选子图的近似图, 由于每个子图被删除的点或边的数量不超出最大值, 保证了所有结果都是候选子图的近似图; 同时, 由于任意一个子图都删除了允许删除的最多的点或边, 保证了任意两个结果不具有包含关系.
4.2 近似子图匹配为了对每个候选子图, 生成对应的近似匹配, 本文设计了一种在单图中查询给定子图的所有同构图的算法.给定图
为了完成上述要求, 需要对所有的可能匹配进行最大的约束, 使得算法能尽早过滤掉错误匹配.为此, 本文设计了一种贪心算法, 为给定图中的所有点, 生成一个匹配顺序.
算法首先初始化点的匹配顺序
(1) 对任意一个未插入匹配顺序的结点, 其邻居结点中, 已插入匹配顺序的结点数量最多的结点.即令
(2) 若符合条件(1)的有多个点, 则对任意一个符合条件(1)的结点, 选择其邻居结点与最多个已在匹配顺序中的结点, 同时也是邻居的结点.即令
(3) 若符合条件(2)的点仍有多个, 则对任意一个符合条件(2)的点, 选择存在最多个满足条件的邻居结点的点, 即邻居结点与任意一个已插入匹配顺序的点都不相邻.即令
(4) 若符合条件(3)的点仍有多个, 则选择其中在目标图中拥有最少对应标签的点, 即设目标图为
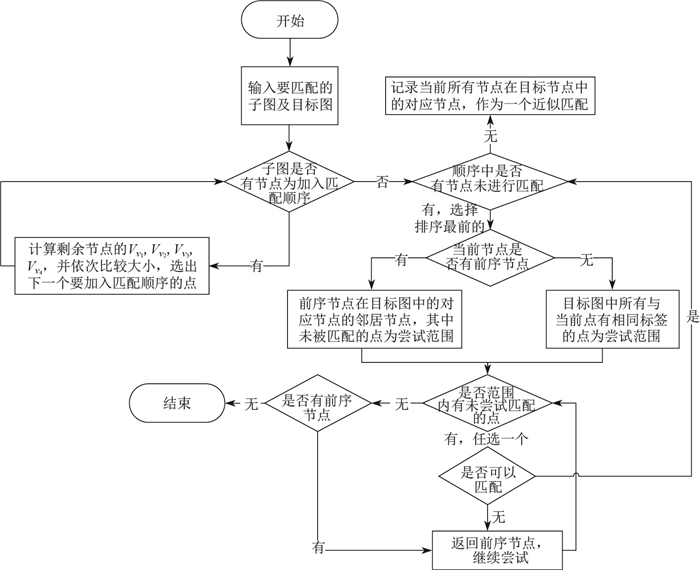
获得匹配顺序后, 算法根据匹配顺序, 对任意一个未匹配的点, 遍历目标图中的点, 检测是否符合匹配要求, 若符合要求, 则记录该匹配, 并按顺序寻找下一个未匹配点的匹配; 若不符合, 则跳过该点, 尝试目标图中的下一个点进行匹配.算法通过匹配顺序, 对任意一个未匹配的点, 仅计算其前一个已匹配的点的所有对应点的邻居结点中, 未被匹配到任何一个点上的点, 具体见图 7.
|
图 7 近似子图匹配流程示意图 Fig.7 Process of approximate subgraph matching |
在获得了每个候选子图在给定图中的近似匹配后, 需要判断一个候选子图是否是近似频繁图.根据子图的近似支持度的定义(定义5), 一个候选子图的支持度应该是候选子图所有近似匹配中, 可能的互斥的近似匹配的最大数量.然而, 确定这个最大数量可以被转化为最大独立集(Maximum Independent Set, MIS)问题, 这是一个NP-complete的问题, 因此计算一个候选子图的准确近似支持度是十分耗时和困难的.
然而, 在本文的情况下, 在计算子图的匹配时, 已经利用的是子图的近似匹配, 因此一个候选子图的准确近似支持度其实不是非常重要.此处本文参考了gApprox算法中支持度的计算方式, 为每个候选子图的近似支持度计算了一个上限阈值, 本文相信这个阈值在本文问题中已经足够可以作为参考, 来判断一个候选子图是否近似频繁.计算方式如下.
(1) 将候选子图的一个匹配图的顶点作为一个集合, 初始化近似支持度上限为0.
(2) 计算候选子图的所有匹配图的点集中的点的出现次数, 即每个点出现在多少个匹配图中, 并按数字从大到小排序.
(3) 选择出现次数最高的点, 若有多个, 则任选一个, 将近似支持度上限加1, 删除所有包含该点的匹配图的点集, 并更新每个点的出现次数.
(4) 不断迭代第(3)步, 直到所有的点集都被删除.
假设有一个候选子图的所有近似匹配有
定理4 所有候选子图的真实近似支持度都不超过上述算法中的支持度上限.
证明 由于对于任意一个点, 只记录一次近似匹配, 即只将支持度上限加1, 相当于记录了一个包含该点的近似匹配, 则保证了记录的近似匹配至少在该点上是互斥的.但由于并不保证在所有点上都是互斥的, 因此支持度上限必然大于或等于真实的近似支持度.
5.2 结果展示通过上节算法计算, 可以获得每一个候选近似频繁子图的近似支持度; 在与给定的支持度阈值进行比较之后, 可以最终确定一个候选近似频繁子图是否频繁.为了提高算法结果的展示效果, 以及提高算法效率, 对算法挖掘结果的展示作以下约束.
第一, 对具有相同结构, 以及相同标签的结果图, 只在结果中展示一次.
第二, 对于每个结果图, 需展示其点的ID和标签, 以及边的左右两点的ID和标签, 其中ID是重新编辑的.
第三, 对于每个结果图, 展示其近似频繁程度和全部对应.
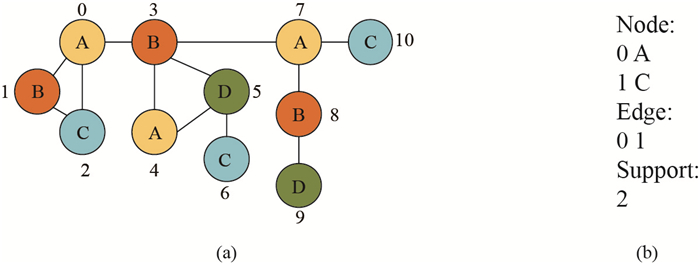
以上约束中, 第一条的原因是在候选子图的生成中, 可能有多个具有相同标签和结构的子图, 由于其在给定单图中的位置不同, 可能出现多次.如图 8(a)中, 点0和点1组成的图, 与点4和点3组成的图结构和标签都相同, 但在图中的位置不同, 因此会在候选子图生成的过程中出现两次.为了提高算法效率, 在记录候选子图时, 仅记录其中一个, 对生成的每一个候选子图, 首先与已经被记录的候选子图作比较, 若果有相同结构和标签的记录, 则不再记录此子图.对于第二条与第三条约束, 主要目的是为了更好地理解近似频繁子图的结构, 以及更好地展示其近似匹配.如图 8(a)中的点0和点2组成的子图, 若其为近似频繁子图, 则显示结果为图 8(b).
|
图 8 结果展示例图 Fig.8 Sample result illustration |
本文设计了两种实验来证明本文算法的有效性, 以及发现更多近似频繁子图的能力.第一种实验为有效性试验, 实验分别在真实数据及人工数据上进行.第二种实验仅基于人工数据, 用于证明本文算法与使用近似程度绝对值算法相比, 本文算法可以发现更多的近似频繁子图.所有实验的真实数据抽取自PPI网络, PPI网络获取自DIP(Database of Interacting Proteins)数据库(http://dip.doe-mbi.ucla.edu), 人工数据由NetworkX工具(https://networkx.github.io/documentation/stable/)构建.所有实验都在1台Windows设备上完成, 设备配置为CPU i5-4690, 8 GB MEM.实验程序由Java完成.据本文所知, 目前已有的与本文算法目的最接近的算法为AGraP, 因此本文所有实验中的对比实验为AGraP算法, 本文仅修改了AGraP中的近似度计算公式与支持度计算方式, 使对比实验基于同一种相似度公式, 从而降低不同相似度公式造成的影响.
由于对比算法AGraP在使用子图大小相关的相似度时效率较低, 算法时间和空间消耗随给定图大小的增长而增长过快, 受条件限制, 无法完成对普通大小的图的挖掘.因此本文通过NetworkX工具分别生成了7个、9个、11个、13个点的样本图(
| 表 1 样本图上挖掘的时间消耗对比 Tab. 1 Comparison of time required for mining of sample graph |
通过表 1可知, 本文算法相对于AGraP算法有较大优势, 且由于AGraP算法时间消耗随图大小增长过快, 因此不适于对较大的图的挖掘, 而本文算法随着图大小的增长, 虽然时间消耗有所增加, 但增长速度相对较为合理.
除了在样本图上的对比实验, 本文利用本文算法, 对规模更大的图进行了挖掘, 从而展示本文算法除了可以应用于十分小的样本图, 同样可以应用于较大规模的图.本文在人工数据与真实数据上都进行了实验.人工数据同样由NetworkX工具生成, 为了显示算法效率随图大小的变化, 分别生成了100个、125个、150个、175个、200个点的不同大小的图.
实验真实数据来自于PPI网络. PPI网络为蛋白质交互网络, 其中包含多种已被发现的蛋白质及蛋白质交互反应.其中有多条蛋白质对拥有高于10
|
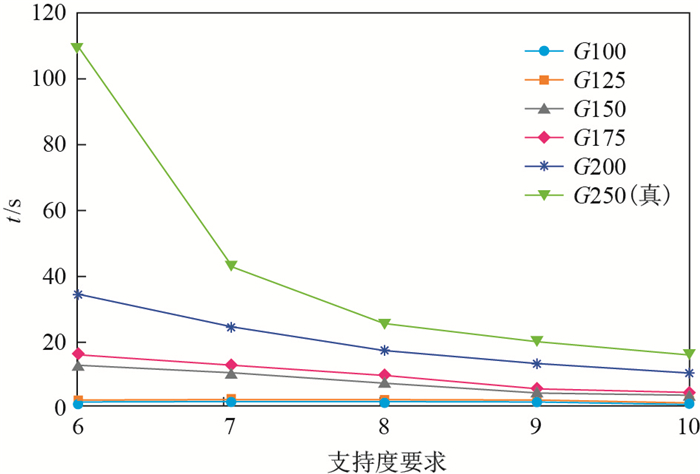
图 9 算法时间消耗随支持度要求的变化 Fig.9 Time required varies with support requirements |
|
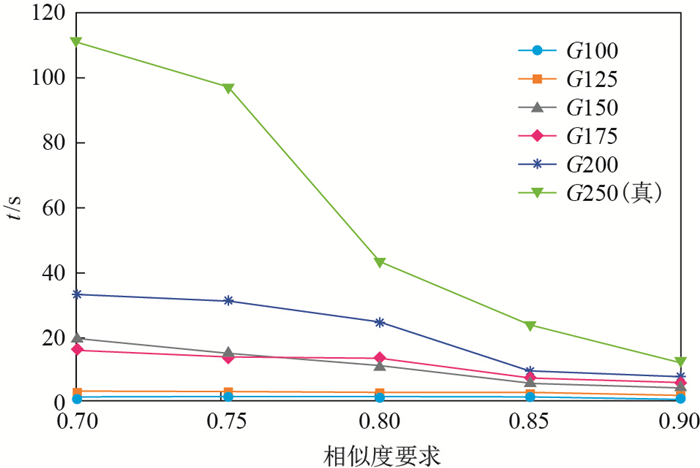
图 10 算法时间消耗随近似程度要求的变化 Fig.10 Time required varies with approximation |
从图 9、图 10中可以发现, 算法的时间消耗随近似支持度要求的提升不断降低, 原因是随着近似支持度要求的提升, 更多的候选子图在早期被过滤掉.根据局部反单调性的特点, 其特定大小范围内的超图都不可能是频繁的, 因此减少了需要生成近似子图及近似子图匹配的候选子图数量, 大大节省了时间消耗.同样地, 随着近似程度要求的降低, 每个候选子图会拥有更多的近似子图, 因此需要进行匹配的近似子图增加.同时, 更多的候选子图被判定为频繁, 因此时间消耗上升.除此之外, 给定单图的大小对时间消耗也具有较大的影响, 原因是随给定单图大小增加, 其候选子图的数量呈指数上升, 因此时间消耗上升.
除上述实验, 本文还在样本图上进行了对比实验, 实验主要比较本文算法发现的近似频繁子图数量, 与利用近似程度绝对大小的算法发现的近似频繁子图的数量的区别.实验利用的样本图为图 8(a).实验对比算法为本文算法的修改版, 即近似程度计算公式为缺失的点或边的绝对值.实验设置近似程度相对值
| 表 2 发现子图能力结果 Tab. 2 Experimental results showing the ability to discover subgraphs |
如表 2所示, 本文算法利用候选子图大小相关的近似度相对值计算公式, 在近似支持度设置为3时, 发现候选子图B-A-C为近似频繁子图, 而对比算法利用缺失点或边的绝对值, 则忽略了该候选子图.
7 结论随着数据规模的增加和数据中可能产生的噪音数据量的增长, 近似频繁子图挖掘算法将受到越来越广泛的关注.因此, 近似频繁子图挖掘算法需要根据候选子图大小, 来判断可容忍的噪音数据量的多少, 即可容忍的数据缺失数量是多少.本文设计了一种利用候选子图大小相关的近似程度计算公式, 从而允许不同大小子图缺失不同数量的点或边的近似频繁子图挖掘算法.该算法利用缺失点或边的数量与子图大小的百分比作为近似程度计算的标准, 通过候选子图生成, 近似子图生成及匹配, 近似支持度的计算几个步骤, 实现了候选子图大小相关的近似频繁子图挖掘算法.人工数据和真实数据上的实验都表明, 本算法效率更高, 且能发现利用缺失点或边数量绝对值作为近似程度的算法不能发现的候选子图.在未来的工作中, 希望能进一步提高算法效率, 使得算法能在大规模数据上应用.
| [1] |
YAN X F, HAN J W. gSpan: Graph-based substructure pattern mining[C]//Proceedings of the 2002 IEEE International Conference on Data Mining. 2002: 721-724.
|
| [2] |
ELSEIDY M, ABDELHAMID E, SKIADOPOULOS S, et al. GraMi:Frequent subgraph and pattern mining in a single large graph[J]. Proceedings of the VLDB Endowment, 2014, 7: 517-528. DOI:10.14778/2732286.2732289 |
| [3] |
CHEN C, YAN X F, ZHU F D, et al. gApprox: Mining frequent approximate patterns from a massive network[C]//7th IEEE International Conference on Data Mining. 2007: 445-450.
|
| [4] |
FLORES-GARRIDO M, CARRASCO-OCHOA J A, MARTÍNEZ-TRINIDAD J F. AGraP:An algorithm for mining frequent patterns in a single graph using inexact matching[J]. Knowledge and Information Systems, 2015, 2(44): 385-406. |
| [5] |
KURAMOCHI M, KARYPIS G. Finding frequent patterns in a large sparse graph[J]. Data Mining and Knowledge Discovery, 2005, 11(3): 243-271. |
| [6] |
NIJSSEN S, KOK J N. A quickstart in frequent structure mining can make a difference[C]//Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2004: 647-652.
|
| [7] |
ALONSO A G, PAGOLA J E M, CARRASCO-OCHOA J A, et al. Mining frequent connected subgraphs reducing the number of candidates[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. 2008: 365-376.
|
| [8] |
RANU S, SINGH A K. Graphsig: A scalable approach to mining significant subgraphs in large graph databases[C]//2009 IEEE 25th International Conference on Data Engineering. 2009: 844-855.
|
| [9] |
CHENG H, YAN X F, HAN J W. Mining graph patterns[C]//Frequent Pattern Mining, Berlin: Springer, 2014: 307-338.
|
| [10] |
KRISHNA V, SURI N R, ATHITHAN G. A comparative survey of algorithms for frequent subgraph discovery[J]. Current Science, 2011, 190-198. |
| [11] |
CHOUDHURY S, PUROHIT S, LIN P, et al. Percolator: Scalable pattern discovery in dynamic graphs[C]//Proceedings of the 11th ACM International Conference on Web Search and Data Mining. 2018: 759-762.
|
| [12] |
INGALALLI V, IENCO D, PONCELET P. Mining frequent subgraphs in multigraphs[J]. Information Sciences, 2018, 451/452: 50-66. DOI:10.1016/j.ins.2018.04.001 |
| [13] |
ALGULIEV R M, ALIGULIYEV R M, GANJALIYEV F S. Extracting a heterogeneous social network of academic researchers on the Web based on information retrieved from multiple sources[J]. American Journal of Operations Research, 2011, 1(2): 33. |
| [14] |
LIMA JR D P, GIACOMINI H C, TAKEMOTO R M, et al. Patterns of interactions of a large fish-parasite network in a tropical floodplain[J]. Journal of Animal Ecology, 2012, 81(4): 905-913. DOI:10.1111/j.1365-2656.2012.01967.x |
| [15] |
GAO X B, XIAO B, TAO D C, et al. A survey of graph edit distance[J]. Pattern Analysis and Applications, 2010, 13(1): 113-129. |
| [16] |
HIDOVIĆ D, PELILLO M. Metrics for attributed graphs based on the maximal similarity common subgraph[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2004, 18(3): 299-313. |
| [17] |
DEHMER M, EMMERT-STREIB F. Comparing large graphs efficiently by margins of feature vectors[J]. Applied Mathematics and Computation, 2007, 188(2): 1699-1710. |
| [18] |
HOLDER L B, COOK D J, DJOKO S. Substucture discovery in the SUBDUE system[C]//KDD Workshop, 1994: 169-180.
|
| [19] |
JIA Y, ZHANG J T, HUAN J. An efficient graph-mining method for complicated and noisy data with real-world applications[J]. Knowledge and Information Systems, 2011, 28(2): 423-447. DOI:10.1007/s10115-010-0376-y |
| [20] |
FLORES-GARRIDO M, CARRASCO-OCHOA J A, MARTÍNEZ-TRINIDAD J F. Extensions to AGraP algorithm for finding a reduced set of inexact graph patterns[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2018, 32(1): 1860012. |
| [21] |
ACOSTA-MENDOZA N, GAGO-ALONSO A, CARRASCO-OCHOA J A, et al. Extension of canonical adjacency matrices for frequent approximate subgraph mining on multi-graph collections[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2017, 31(8): 1750025. DOI:10.1142/S0218001417500252 |
| [22] |
ACOSTA-MENDOZA N, MORALES-GONZáLEZ A, GAGO-ALONSO A, et al. Image classification using frequent approximate subgraphs[C]//Iberoamerican Congress on Pattern Recognition. 2012: 292-299.
|
| [23] |
ACOSTA-MENDOZA N, CARRASCO-OCHOA J A, MARTÍNEZ-TRINIDAD J F, et al. Image clustering based on frequent approximate subgraph mining[C]//Mexican Conference on Pattern Recognition. 2018: 189-198.
|