0 引言

市民出行最后1 km问题一直是困扰城市交通出行的难点, 近几年, 随着摩拜、OFO等共享单车企业的出现, 这一问题一度得到了缓解.然而, 伴随着共享单车在中国各大城市的广泛应用, 在缓解城市交通压力与方便人们出行的同时, 共享单车的乱停乱放在很大程度上也影响了城市的正常交通秩序.共享单车大多被投放于POI(Point of Interest)(比如地铁站、公交站、电影院、大型购物场所、体育场、火车站、大型居民区等)附近, 忽略了POI区域以外的其他热门用车区域, 如因交通意外、临时道路封锁导致机动车无法正常通行的道路区域等.此外, 不同的日期(如工作日/节假日)、同一天中不同的时段, 以及不同的天气状况都会影响用户的用车需求.普遍采用的共享单车投放策略由于忽略了这些外部因素, 直接导致了大量单车闲置在没有用车需求的POI附近, 而大部分用户的单车使用需求却无法满足, 这与共享单车最早的投放初衷相违背.

随着移动设备的广泛应用和位置采集技术的蓬勃发展, 出租车作为一种非常重要的城市出行工具, 广泛地长时间分布于城市路网中.出租车车上装备的GPS设备, 以一定的时间间隔不断地向出租车信息管理中心发送其实时的位置信息, 包括出租车ID、载客状态、时间戳、经纬度坐标、速度等数据.通过对出租车历史轨迹数据的挖掘分析, 可以有效提取出租车的移动行为模式, 进而洞察城市的交通出行规律.已有大量学者基于出租车历史轨迹数据, 对载客热门区域提取^[1-2]、线路规划^[3-4]等问题进行了较为深入的研究.鉴于共享单车企业普遍使用POI附近投放单车策略而忽略不同日期、不同时段单车使用需求的差异性, 导致共享单车的低效使用, 本文考虑使用短程的出租车轨迹数据(出行距离在3 km以下), 分时段获取城市不同区域的热门短途出行需求.

目前国内各大中城市的共享单车数量已趋于饱和, 基于有限数量的共享单车资源, 要确保满足各时段热门出行区域的用车需求, 亟需设计一个共享单车的实时投放和调度策略(含调度车的行车线路), 这实质上涉及了两个子问题:第一, 分时段提取城市热门短程出行区域; 第二, 结合实时路况信息的共享单车动态调度.这两个问题所面临的关键挑战在于: ①预估不同时段内的用车需求变化情况, 这需要考虑诸多其他外部因素影响, 比如不同的日期(工作日/节假日)、同一天中不同的时段, 以及不同的天气状况; ②预估不同时段城市各路段的共享单车停车情况; ③合理规划单车调度车辆的行车线路.

近年来, 国内外不少学者对城市公共自行车的需求预测和调度策略进行了深入探讨, 其中预估用车需求的研究大多基于历史用车需求均值或历史用车记录数据. Eoin等研究了城市高峰时段单车使用情况^[5], 通过分析城市公共自行车系统数据, 预估各驻车站点单车的用车频次; Dimitrios等通过识别影响单车使用的因素以及城市公共自行车的流动模式, 进而预测单车的用车需求^[6]; Cheng等通过对具有时间相关的PCTMC(Population Continuous Time Markov Chain)模型进行分析^[7], 研究了驻车站点的用车频次预估问题; Chen等提出了一种半监督特征选择法预测用户的出行需求^[8], 即基于历史用车次数的特征选择法精准地预估用车频次; Divya等基于出租车数据, 提出了一种多因素回归模型预测城市公共自行车的用车需求^[9], 但里面混有大量长途出租车数据, 导致短程用车需求预估不精确.

城市公共自行车的调度策略研究大多数采用聚类建模或数学算法建模.比如Liu等提出的自适应能力约束的$K$中心聚类AdaCC$K$C(Adaptive Capacity Constained $K$-center Clustering)算法^[10], 将多车辆行车线路问题简化为内部集群只需1辆调度车的行车线路问题; Fábio等提出的基于迭代的局部搜索ILS(Iterated Local Search)的启发式算法^[11], 筛选满足有用车需求的驻车站点的最低成本行车路线.但这些研究者们都未考虑实时路况对调度效率的影响.

不同于城市公共自行车, 摩拜、OFO等共享单车虽然和城市公共自行车在预测用车需求和调度优化上有相同之处, 但共享单车没有固定的驻车站点, 它可以随取随放.这就衍生出了共享单车的投放问题、停车区域的提取问题和单车动态调度问题, 迄今为止还未有研究试图解决上述问题.基于此, 本文构建了一个两阶段共享单车的实时投放及动态调度框架, 包括离线建模和在线调度:在离线建模阶段, 采用区域提取技术, 基于短程的出租车轨迹数据, 实时获取不同日期(工作日/节假日)各时段内的城市热门用车区域和共享单车停车区域, 所获得的热门区域不仅能准确预估单车投放区域, 还能预估各时段单车的停车情况, 为后续单车调度提供可靠的数据支持; 在线调度部分, 旨在解决单车的动态调度问题, 涉及调度区域与调度效率.如前所述, 城市公共自行车由于有固定的驻车站点, 驻车站点的车储量能满足1 d的需求, 所以城市公共自行车的调度效率要求不高.然而, 共享单车由于用车需求的动态变化, 要确保有限数量的单车资源得到合理使用, 必须根据各时段的用车需求设计更为高效的调度策略.具体来说, 先确定调度区域, 再基于用车区域的用车比例从$k$近邻停车区域中确定待调度的停车区域, 在此基础上, 结合实时交通状况为共享单车调度车推荐top-$k$条路况优选的调度线路.本文的主要贡献如下.

(1) 构建并实施了一个两阶段的共享单车的实时投放与调度框架: ①离线建模部分, 提出了区域提取模型, 采用基于DBSCAN(Density-Based Spatial Clustering of Applications with Noise)分时段最小值支持技术的聚类算法(RET算法), 对短程的出租车历史轨迹进行聚类, 提取各时段内城市热门用车区域及其用车频次、共享单车停车区域及其停车频次; ②在线调度部分, 提出了结合实时交通状况的调度优化模型(ROM方法), 根据用车比例和$k$近邻停车区域的停车比例, 确定待调度的停车区域, 并结合实时路况为共享单车调度车推荐前$k$条路况优选的行车线路, 最终以具有较短的调度车行车里程和行驶时间的路线完成实时调度, 确保满足各时段内单车的用车需求.

(2) 在出租车轨迹数据集上进行了大量对比实验.在预估用车和停车频次上与算法MSI(Multi-Similarity-based Inference)^[13]、MSEW$k$(Multi-Similarity-Equally-Weighted $k$NN)^[10]、IPPI(Inhomogeneous Poisson Process Inference)^[12]、HM(Historical Mean)^[8]等进行对比, 同时与NNIA(Nearest Neighbor Insertion Algorithm)^[16]、GA(Genetic Algorithm)^[17]等进行调度效率的对比.对比实验结果表明, 本文所提方案在预估用车、停车频次的精确度以及调度效率上均优于其他算法.

本文的第1节介绍用车需求预估、共享单车的停车情况预估及调度车的行车线路推荐的相关工作; 第2节对本文相关概念进行形式化定义; 第3节介绍两阶段框架; 第4节介绍实验分析; 第5节总结全文.

1 相关工作 1.1 共享单车用车需求及停车情况预估

共享单车用车需求预估包括热门用车区域的位置预估和各热门用车区域的用车频次预估.根据用车需求预估, 确定共享单车的投放区域和每个投放区域的投放量.共享单车停车情况预估包括共享单车停车区域的位置预估和每个停车区域的单车数量预估.

关于共享单车用车区域和停车区域的位置研究, 由于共享单车随取随放、没有固定驻车站点等特点, 本文使用与共享单车服务直接或间接相关的各类数据来达到预测城市热门用车区域和停车区域位置的效果, 使用出租车的轨迹数据获取热门载客区域^[1-2], 这能为用车区域和停车区域位置预测提供依据.关于现有预估用车频次和停车频次的研究, 大部分是基于历史记录数据的. Alvarez-Valde等提出了IPPI算法^[12], 通过非齐次Poisson过程预测用车和停车频次, 根据历史记录预测用车和停车比例; Chen等提出了HM算法^[8], 将有用车需求的历史记录数据作为用车和停车频次的预测值.除此之外, 还有考虑多影响因素建模以提高用车和停车频次的预估精度, 如, Li等提出的MSI算法考虑了天气、温度、风速与时间的相似性^[13], 似性函数是这3个相似性的乘法, 但这几个因素的权重没有被研究; Liu等提出的MSEW$k$算法是对影响需求预测的不同因素采取相同的权值, 运用混合高斯算法来预测需求^[10].

以上关于单车用车需求及停车情况预估的研究, 虽能提高用车频次及停车频次预估精度, 但都缺乏实时且精确度较高的用车需求和停车情况预估.

1.2 调度车的行车线路推荐

关于行车线路的研究大部分是通过对用车区域和停车区域进行数学建模. Fábio等提出的基于迭代的局部搜索的启发式算法^[11], 是通过一条最优的线路来完成所有调度, 但仅考虑了每天单车使用空闲完成调度, 并未考虑各时段内用车需求的差异性; Christian等提出的混合整数线性规划方法^[14], 但未考虑实时路况, 因此调度效率较低; Liu等运用带约束的$K$中心聚类(AdaCC$K$C)算法对用车区域和单车分布区域进行聚类, 将大型多车辆线路问题简化为各簇内驻车站点间的线路选择问题^[10], 相较于传统的调度策略有一定提升, 但仍缺乏实时且快速的调度.

上述研究未考虑日期、时段与实时路况对单车用车需求的影响, 进而导致用车需求的预估准确率较低.鉴于此, 本文主要研究了共享单车用车需求预估、停车情况预估和调度车的行车线路等问题.具体地说, 本文首先提出RET算法, 基于短程出租车的轨迹数据, 预估各时段的热门交通出行需求及城市各路段的共享单车停车情况; 再运用调度优化模型ROM方法, 动态评测行车里程及所需时长, 从而合理规划调度车的行车线路.

2 概念定义

定义1  路网  城市的路网以无向路网图$G(V, E)$表示, 提取地图中的路段交叉口和路段终点作为路网图中的结点集合$V$.每条路段$r\in E$是从一个结点$v\in V$到另一个结点$v'$($\ne $v)$\in V, r.s =v$和$r.e =v'$分别代表路段的起始结点和终止结点.

定义2  原始轨迹  是由一组起始位置$P_{\rm start}$到终止位置$P_{\rm end}$之间的有序路段的结点序列组成, $RT=P_{\rm start}\to P_{1}\to P_{2}\to P_{3}\to \cdot \cdot \cdot \to P_{n}\to P_{\rm end}$, 其中, 任一有向路段满足$\forall e(P_{i}, P_{i+1})\in E, 1\le i\le $n, $\forall $$P_{i }$={$P_{i}$.id, $P_{i}.s, P_{i.}t, P_{i}$.lon, $P_{i}$.lat, $P_{i}$.v}, 1$\le i\le n$.具体含义见表 1.

定义3  调度线路  调度线路$R={\{}r_{1} \to r_{2}\to \cdots \to r_{n}{\}}$, 是由一系列相邻路段组成的, $\forall r_{i}, r_{i+1} \in R, r_{i}, r_{i+1} \in E$并且$r_{i}$.$e = r_{i+1}$.$s$.

定义4  top-$k$调度  线路top-$k$调度线路是指停车区域到用车区域之间的距离较短且道路较不拥堵的前$k$条调度线路, $R_{s}=${$R_{1}$, $R_{2}$, $\cdots $, $R_{k}$}, 是结合实时路况对所有候选调度线路按照拥堵比例排列评测得到, 表示为$R_{1} < R_{2} < , \cdots, < R_{k }$, 且满足$\forall R_{i}\in R_{s}, R_{1} < R_{i} < R_{k}$.

定义5  时段  时段$T_{s}$是把1 d分为12个时段{00:00~02:00, $\cdots$, 22:00~24:00}, 每个时段有2 h, 即$T_{s}=${$T_{1}, T_{2}, \cdots, T_{12}$}, 其中$T_{1}$={00:00~2:00}, $T_{2}$={2:00~4:00}, $\cdots$, $T_{12}$={22:00~24:00}.

定义6  用车频次  用车频次$n_i.pf(t)$是指短程出租车由该位置区域出发的频次, $n_i.pf(t)=${1, 2, 3, $\cdots $, $n$}, 通过用车频次能预估将投放的相应用车区域的共享单车投放量.

定义7  用车区域  用车区域$N$是指某个时段内用车需求较为密集的区域, 即用车频次达到给定的阈值MinPts(Minimum Points), 即$n_i.pf(t)\ge $MinPts.令$n_i.pa(t)$为该区域所处时段, $n_i.pa(t)$, $t\in T_{s}$.与以往的用车区域挖掘方法不同的是, 本文考虑不同时段内用车区域的规律性, 为用车区域定义时段属性, 在其对应的时间段内, 该区域被视为用车区域, 而超过该时段时, 则不再视为用车区域.

定义8  停车频次  停车频次$g_i.df(t)$是指短程出租车到达该位置区域的频次, $g_i.df(t)=${1, 2, 3, $\cdots $, $n$}, 通过停车频次能预估共享单车相应停车区域的停车量.

定义9  停车区域  停车区域$G$是指在相应时段内停车频次$g_i.df(t)$达到给定阈值MinPts的区域, 即$g_i.df(t)\ge $MinPts, 令$g_i.da(t)$为该区域所处时段, $g_i.da(t)$, $t\in T_{s}$.

定义10  top-$k$停车区域  top-$k$停车区域是指给定用车区域当前位置$P_{\rm current}$和当前时间戳$T_{\rm current}$, 基于时间戳的一系列停车区域集$G_{s}$={$g_{1}$, $g_{2}$, $\cdots $, $g_{i}$, $\cdots $, $g_{n}$}, 推荐算法为搜索距离用车区域最近的前一时段的$k$近邻停车区域, 即

$ \begin{align} G=\arg \min\limits_{{\mathrm {top}}-k}:=\{g_i\vert g_i\in G_S^{S_C^i } \Lambda \forall g_j\in G_S^{S_C^j } :f(g_i)\le f(g_j)\}. \end{align} $

(1)

不同于目前的共享单车投放和调度策略, 本文不仅考虑用车区域实时变化情况, 还对用车区域进行$k$近邻停车区域推荐, 再结合实时路况对调度车进行top-$k$行车线路推荐, 以减少调度车行车里程及所需时长.

3 总体框架

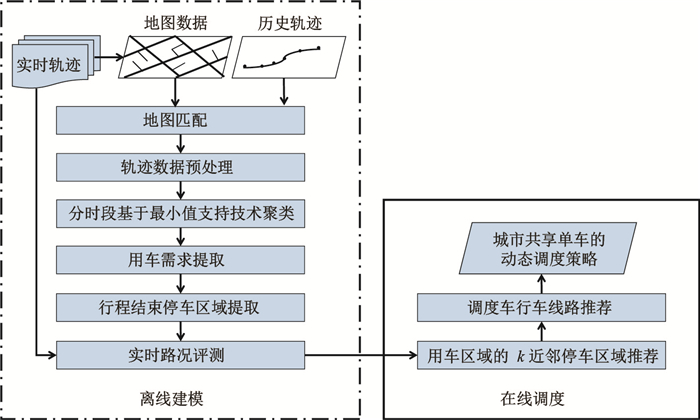
本文构建了一个两阶段的城市共享单车的动态调度框架, 总体框架如图 1所示.整体框架分为离线建模阶段和在线调度阶段.在离线建模阶段, 首先对历史轨迹使用地图匹配技术结合路网数据将有序路段的结点序列映射到真实路段上; 然后对轨迹数据进行预处理, 包括去除有损数据, 将用车点和停车点的数据分别提取出来, 分别对用车点数据和停车点数据进行分时段基于最小阈值支持的聚类, 实现各时段用车需求和行程结束停车区域的提取.基于最小阈值支持的聚类, 是指用车需求频次和停车频次必须达到一定阈值MinPts才能被视为用车区域和停车区域(详见定义7、定义9).聚类技术采用基于密度聚类(DBSCAN)方法, 该方法适于任意形状的轨迹数据聚类并能进一步去噪.在区域提取的过程中, 使用实时轨迹对其进行增量更新, 确保用车区域和停车区域提取的精准性.在线调度阶段, 首先获取当前用车区域的位置信息和所属时段, 搜索距离用车区域最近的前一时段的$k$近邻停车区域, 并根据用车比例和停车比例在初始提取的top-$k$邻近停车区域中选取最终调度的停车区域, 同时结合当前时段出租车轨迹流完成对各路段的交通拥塞情况的评测; 然后根据各线路拥堵比例对每个最终调度的停车区域到用车区域之间的线路进行评测排序, 获取道路畅通的线路, 实现对调度车的top-$k$行车线路的推荐.

3.1 离线建模

离线建模主要考虑区域提取模型。

考虑工作日、节假日, 以及1 d中的不同时段对用车区域和停车区域的影响, 本文将出租车历史轨迹划分为工作日以及节假日两个部分, 并将1 d分为12个时段{00:00~02:00, 02:00~04:00, 04:00~06:00, $\cdots$, 20:00~22:00, 22:00~24:00}, 采用RET算法进行聚类, 完成对不同时段内用车/停车区域的提取.

用车区域提取.用车区域为在某个时段内发生用车需求较为密集的区域(定义7).这些区域通常具有特定的人群移动规律和功能特征, 如受交通意外影响的出行区域、一个大型商业区、学校、旅游景点等.鉴于该区域的用车需求与所在日期/时段的紧密联系, 因此本文考虑获取不同时段内用车密度较大的区域.在现有的用车区域预测研究中, 无法及时洞察用车区域的动态变化, 本文则通过RET算法准确且实时地发现了用车区域.

行程结束停车区域提取.停车区域为在某个时段内发生停车事件较为密集的区域(定义9), 即在该区域停车频次比较大, 且停放的单车数量也比较大.这些区域具有时段属性, 可能在火车站、电影院、公交站等地方, 也可能在一些临时的突发区域.本文通过RET算法实时且准确地发现了停车区域, 并在后续工作中会将这些停车区域的单车调度至下一时段的用车区域, 确保了人们的用车需求, 并从一定程度上缓解了共享单车的乱停乱放现象.

本文根据出租车轨迹数据提取用车和停车区域数据, 考虑如下:鉴于共享单车解决最后1 km的交通问题, 本文从出租车行程不超过3 km的历史轨迹数据中提取由空载状态跳转为载客状态的GPS样本点, 并将其视为用车点; 将载客状态跳转为空载状态的GPS位置点视为停车点.在提取用车区域与停车区域时, 本文基于广泛采用的轨迹聚类算法DBSCAN提出了RET算法.关于DBSCAN算法的重要参数$ r_{\rm spatio}$和MinPts($ r_{\rm spatio}$表示空间维度的度量半径, MinPts表示形成簇所要求的最少点数量), 使用基于实际轨迹数据集多次调参获得的较优值.通过RET算法聚类获取数据点密度较大的簇, 确保位于同一簇中的用车/停车点在地理位置上距离邻近, 伪代码如算法1所示.

算法1 RET based on DBSCAN

输入: A list of point $D$={$p_{1}, p_{2}{, {\cdots}, p}_{n}$}, MinPts, $ r_{\rm spatio}$

输出: $C$: Clustering result clusterList

$C$ $\leftarrow $ 0, cluster_$i\leftarrow $1;

Initialize $D$, TaxiID_i, $D_{s}^{\rm pick}$, $D_{s}^{\rm drop}$, C;

1:     for each point $ p_{j}$ in $D$ do

2:       if($ p_{i}$.id=TaxiID_i.id)do

3:         for each point $ p_{j }$ in TaxiID_i do

4:           if ($p_{i}$.time$ < p_{j}$.time)then

5:              TaxiID_$i\leftarrow p_{j}=p_{i }\cup p_{j+1}=p_{j }$;

6:          else if ($p_{i}$.time$\ge p_{j}$.time)then

7:              TaxiID_$i\leftarrow p_{j+1}=p_{i}$;

8:        else TaxiID_$i++\leftarrow p_{i }$;

/*find short-distance taxi routes, record the drop-off and pick-up point*/

9:    if($p_{m }$and $p_{n }$ is the pick-up and drop-off points of a trip)do

10:           if(dist$\vert $$p_{m}, p_{n}$$\vert$$\le $3 km $\vert \vert $T$_{s}$.start$\le p_{n}$.time, $p_{m}$.time$\le T_{s}$.end)then

11:             $D_{s}^{\rm pick}\leftarrow p_{n }$; $D_{s}^{\rm drop}\leftarrow p_{m}$;

12:    for each point $ p_{e}$ in $D_{s}^{\rm pick}$, $D_{s}^{\rm drop}$do

13:          While!$p_{e}$.isVisited=true do;

/*find the Neighborhood points for $p_{e }$: Nr$_{\rm spatio}p_{e}$*/

14:         if($\vert $ Nr$_{\rm spatio}p_{e}$$\vert $$\ge $MinPts)then

15:           $p_{e}$.cluster_ID=cluster_$i$;

16:           for each Neighborhood point $ p_{a}$ in Nr$_{\rm spatio}p_{e}$ do;

17:           While!$p_{a}$.isVisited=true do;

/*find the Neighborhood points for $p_{a}$ about $r_{\rm spatio}$: Nr$_{\rm spatio}p_{a}$ */

18:           if($\vert $ Nr$_{\rm spatio}p_{a }\vert \ge $MinPts)then

19:             Nr$_{\rm spatio}$pi$\leftarrow r_{\rm spatio} p_{i}\cup r_{\rm spatio} p_{a}$

20:             if($p_{a}$.cluster_ID=0)then

21:                $p_{a}$.cluster_ID=cluster_$i$;

22:            cluster_$i$++;

23:   resturn $C$;

算法1中$D$为GPS位置点集合, $C$为聚类结果的集合, TaxiID_i为同一出租车的GPS位置点集合, $D_{s}^{\rm pick}$表示用车点数据集, $D_{s}^{\rm drop}$表示停车点集合, Nr$_{\rm spatio}p_{e}$为点$p_{e }$邻近的点集合.算法1的具体功能如下:首先从原始数据中提取每辆出租车所有的GPS点并按时间先后顺序存储(行1-8), 然后提取出租车行程不超过3km的历史轨迹数据并将行程开始的GPS点放入相应时段的用车点集合中, 行程结束的GPS点放入相应时段的停车点集合中(行9-11);接着分别对每个时段的用车点集合和停车点集合中的点$p_{i}$搜索离其在空间维度上相邻的点, 如果相邻点的数量大于等于MinPts, 就把$p_{e}$标记为核心点, 并建立新簇$p_{e}$.cluster_ID, 并将$p_{e}$领域内所有点加入$p_{e}$.cluster_ID中(行12-15);最后对所有未被访问的$p_{e}$邻域内的点$p_{a}$, 再次搜索$p_{a}$的邻近点, 如果相邻的点数量至少为MinPts个, 就把这些相邻点中未归入任何一个簇的点加入$p_{e}$.cluster_ID簇中(行16-23).

对于工作日/节假日产生的出租车轨迹, 使用RET算法分时段提取用车点和停车点位置并对其进行聚类, 获得的各时段中空间密度较高的用车点与停车点区域, 代表不同时段内用车、停车事件发生较为频繁的区域, 各簇的簇心表示用车区域与停车区域的位置.

3.2 在线调度

获取工作日、节假日中各时段的用车和放车区域集, 该部分工作以离线的方式进行处理.在线调度阶段中, 提出ROM方法, 首先为用车区域推荐$k$个近邻停车区域, 然后结合实时路况实现调度车行车线路推荐.

3.2.1 $k$近邻停车区域推荐

对当前用车区域进行$k$近邻停车区域推荐.对于一个给定位置$P_{\rm current}$、时间戳$T_{\rm current}$的用车区域而言, 搜索与其邻近的前一时段的停车区域, 将用车区域当前位置$P_{\rm current}$的簇心$C^{\rm heart}_i$与附近停车区域之间的最短距离线路作为选取附近top-$k$停车区域的评测标准, 完成用车区域的$k$邻近停车区域推荐.

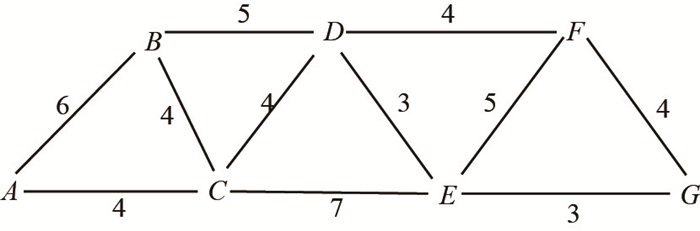
采用Dijkstra算法^[15]作为寻路策略, 完成对用车区域簇心到停车区域簇心的最短线路的计算. Dijkstra算法通过距离权值$SP$找到从一个结点到任何其他结点的最低权重线路.该方法将在下文的最短线路函数$S_{\rm cost}$中得到充分运用.本文采用Dijkstra算法找到了离用车区域距离最短的top-$k$停车区域.以一个带有权值的无向图为例, 如图 2, 令$A$为用车区域簇心, $G$为停车区域簇心, 用Dijkstra算法分析从用车区域簇心$A$到停车区域簇心$G$的最短线路.

步骤1  以带有权值的一个矩阵$z$表示含有各结点的带权无向图, 矩阵相应位置的数值代表对应线段的权值, 如果从一个结点到另一个结点不连通, 那么其矩阵中的值为$\infty $.带权值的邻接矩阵图如图 3所示.

设用车区域簇心$A$为起始结点, 停车区域簇心$G$为目的结点, $S_{i}$代表从结点$A$到有向图中其他结点的最短线路长度.设置初始值: $S_{i}= < A$, $v_{i} > $, $v_{i}\in {A, B, C, D, E, F}$, $Q$代表标记的结点集合.

步骤2  选择$v_{j, }$使$S(j)$=min{$S(i)\vert v_{i}$. $\in \{B, C, D, E, F\}$}, $v_{j}$是从结点$A$出发找出一条最短线路的终止结点, 令$Q\leftarrow $Q$\cup ${$v_{j}$}.

步骤3  修改起始结点$A$, 再次到集合$\{B, C, D, E, F\}$中任一结点$v_{n}$之间的最短线路的长度值, 若$S(j)+z(j, n) < S(n)$, 那么$S(n)=S(j)+z(j, n)$;

步骤4  重复步骤2、步骤3, 最终得到从起始点$A$到其他结点的最短距离线路, 并对线路的长度递增进行排序.

基于以上最短距离线路的计算方法, 本文采用欧氏距离计算方法获取基于用车区域当前位置$P_{\rm current}$到各停车区域的最短线路path(path$_{i}=P_{\rm current}$$\to P_{1}$ $\to P_{2}$$\to $$\cdot \cdot \cdot $$\to $$P_{n}$$\to $$C_{i}^{\rm heart}) $, 完成用车区域的$k$近邻停车区域推荐.对应的公式为

$ \begin{equation} S_{\rm cost}=S(P'_{\rm current}, P'_1)+\sum\limits_{i=1}^n S (P' _i, P'_{i+1})+S(P'_n, C_i^{\rm heart}). \end{equation} $

(2)

公式(2)中$S_{\rm cost}$表示用车区域到停车区域的线路长度, $S(P'_{\rm current}, P'_{1})$表示当前位置$P'_{\rm current}$到道路交叉口$P'_{1}$的距离, $S(P'_ i, P'_{ i+1})$代表边$e(P'_{i}, P'_{i+1})$的长度, $S(P'_n, C_i^{\rm heart})$代表交叉口$P'_{n}$到单车分布区域$C_i^{\rm heart}$的簇心距离, 最后根据$S_{\rm cost}$找到离用车区域最近的top-$k$停车区域.

确定最终调度的停车区域.根据用车区域的用车比例及其近邻的top-$k$停车区域的停车比例, 计算出该用车区域具体需要调度的停车区域.接下来将统计各时段用车比例及其top-$k$停车区域的停车比例.相应的公式分别为

$ \begin{align} N_{i}=\frac{n_i.pf(t)}{\sum\limits_{i=1}^m {(n_i.pf(t)+g_i.df(t))} }, \end{align} $

(3)

$ \begin{align} G_i=\frac{g_i.df(t)}{\sum\limits_{i=1}^m {(n_i.pf(t)+g_i.df(t))} }. \end{align} $

(4)

公式(3)中, $N_{i}$为用车比例, $n_i.pf(t)$表示特定用车区域的用车频次; 公式(4)中, $G_{i}$为停车比例, $g_i.df(t)$表示特定停车区域的停车频次; 公式(3)、公式(4)中$\sum\limits_{i=1}^m {(n_i.pf(t)+g_i.df(t))} $表示该时段所有用车和停车区域的用车、停车频次.

3.2.2 调度车的行车线路推荐

对于(下一时段的)用车区域应考虑距离其最近的$k$个(上一时段的)停车区域, 在此基础上, 结合实时路况为单车调度车辆规划(下一时段的)用车区域到(上一时段的)停车区域之间距离最近且交通较畅通的线路.本文根据拥堵比例来评测交通状况.首先计算出各路段的速度, 通过基于滑动窗口的轨迹流聚类算法OCluST(Online Clustering Streaming Trajectorys)^[16]获得各路段基于时间$T_{\rm current}$的实时速度.该方法通过对实时到达的出租车轨迹进行增量式聚类分析, 实时提取各簇的移动行为模式, 实现对各簇所在路段的实时交通状况评测.为了更为直观地在地图上展示道路状况, 本文将道路交通状况分为两种:速度低于30 km/h的将其视为交通缓慢(以黄色标记); 速度超过30 km/h的定义为交通畅通(以绿色标记).

获取各路段的实时速度后, 则可计算各行车线路的拥堵情况.将交通缓慢的路段长度和总线路长度进行比例分析, 并对所有线路按拥堵比例排序.从而完成停车区域到用车区域的调度车的行车线路推荐.拥堵比例(Traffic Congestion Ratio, TCR)计算公式为

$ \begin{equation} {\rm TCR}=\frac{\sum\limits_{i=1}^h {r_i } }{S_{\rm all}}, \end{equation} $

(5)

其中, $\sum\limits_{i=1}^h {r_i } $为特定行车线路中交通缓慢路段的总长度, $S_{\rm all}$为特定停车区域到用车区域之间的所有推荐行车线路的总里程.

4 实验 4.1 实验环境及数据集

本文实验采用上海2015年4月共30d的出租车轨迹数据集, 该数据集包含近13 600辆出租车的GPS轨迹数据.离线建模阶段, 首先基于前25d的历史轨迹数据$C_{1}$提取用车区域和停车区域; 在线调度阶段基于后5d的轨迹数据$C_{2}$模拟实时到达轨迹, 通过各时段内实时到达的出租车轨迹分析路网交通情况, 利用$C_{1}$提取各时段内的用车区域和停车区域, 利用$C_{2}$对实时交通路况进行评测, 其中出租车的GPS数据格式如表 2所示.实验使用Java语言实现算法的编写, 在Windows 7操作系统, 机器配置为2.50 GHz Intel Core i5处理器和12 GB物理内存的PC机上运行.

4.2 评测标准

本文提出的RET算法, 对用车点和停车点进行时空聚类, 该算法不仅能预测用车和停车区域位置, 还能预测相应区域的用车和停车频次.本文将RET算法与MSI^[13]、MSEW$k$^[10]、IPPI^[12], HM^[8]进行有效性对比实验.采用的衡量性能的标准是对每个时段用车频次和停车频次预测的平均绝对误差(Mean Absolute Error, MAE), ${\rm MAE}^{\rm pick}$表示用车频次预测误差, $\rm {MAE}^{\rm drop}$停车频次预测误差.公式分别为

$ \begin{equation} \label{eq4} \mathrm {MAE}^{\rm pick}=\frac{\mbox{1}}{T}\sum\limits_{t=1}^T {\frac{\sum\nolimits_{i=1}^m {\left| {\hat {n}_i.pf(t)-n_i.pf(t)} \right|} }{m}} , \end{equation} $

(6)

$ \begin{equation} \label{eq5} {\rm MAE}^{\rm drop}=\frac{\mbox{1}}{T}\sum\limits_{t=1}^T {\frac{\sum\nolimits_{i=1}^m {\left| {\hat {g}_i.df(t)-g_i.df(t)} \right|} }{m}} . \end{equation} $

(7)

公式(6)中, $n_i.pf(t)$表示各时段用车区域的真实用车频次, $\widehat {n}_i.pf(t)$表示相应用车区域的预测值; 公式(7)中, $g_i.df(t)$表示各时段停车区域的真实停车频次, $\widehat {g}_i.df(t)$表示相应停车区域的预测值.

本文提出的实时调度优化模型(ROM方法)能以较短调度车的行车线路总里程和较短行车总时长的方式快速完成单车调度, 确保下一时段的用车需求.行车线路总里程越小代表单车公司运营成本越低, 总行车时长越短越能快速的完成整个调度过程.本文将所提出的调度优化模型与其他调度优化算法NNIA^[17]和GA^[18]进行了有效性对比实验.衡量ROM方法性能的标准是行车线路总里程(Total Mileage of Driving Routes, TMR)和行车总时长(Total Driving Time, TDT), 相关公式分别为

$ \begin{align} \label{eq6} {\rm TMR}=\sum\limits_{i=1}^l {S_{\rm cost}^i } , \end{align} $

(8)

$ \begin{align} \label{eq7} {\rm TDT}=\sum\limits_{i=1}^l {T_{\rm cost}^i } , \\ \end{align} $

(9)

$ \begin{align} \label{eq8} T_{\rm cost}=\frac{S(P_{\rm current}, P_1)}{\mathrm {speed}(P_{\rm current}, P_ 1)}+\sum\limits_{i=1}^{n-1} \left({\frac{S(P_i, P_{i+1})}{\mathrm {speed}(P_i, P_{i+1})}} +\frac{S(P_n, C_i^{\rm heart})}{\mathrm {speed}(P_n, C_i^{\rm heart})}\right). \end{align} $

(10)

公式(8)中, TMR表示完成本时段所有调度的行车线路总里程, 该公式基于调度车行车线路里程$S_{\rm cost}$(详见公式(2)); 公式(9)中TDT为完成该时段所有调度的行车总时长, $T_{\rm cost}$ 为特定行车线路的行车时长; 公式(10)中, $T_{\rm cost}$ 为行车时间长, $S(P_{\rm current}, P_1)$和speed$(P_{\rm current}, P_1)$分别表示当前位置$P_{\rm current}$到道路交叉口$P_{1}$的距离和实时速度; 类似的, $S(P_i, P_{i+1})$和speed$(P_i, P_{i+1})$分别代表边$e(P_{i}, P_{i+1})$的长度和实时速度, $S(P_n, C_i^{\rm heart})$和speed$(P_n, C_i^{\rm heart})$分别代表交叉口$P_{n}$到停车区域$C_i^{\rm heart}$的簇心距离和实时速度.

4.3 实验效果

为了展示单车调度效果, 本文选取出行需求相对密集的上海外滩周围区域作为实验区域, 该区域范围满足经度lon$\in $[121.417041, 121.516261]、纬度lat$\in $[31.197382, 31.239589].

4.3.1 用车频次及停车频次预测

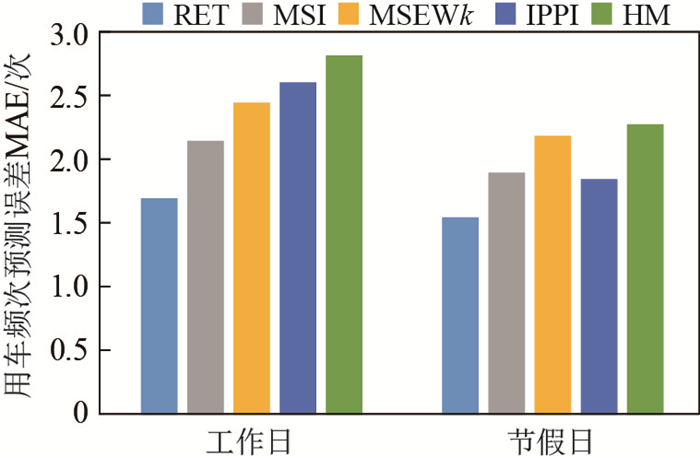
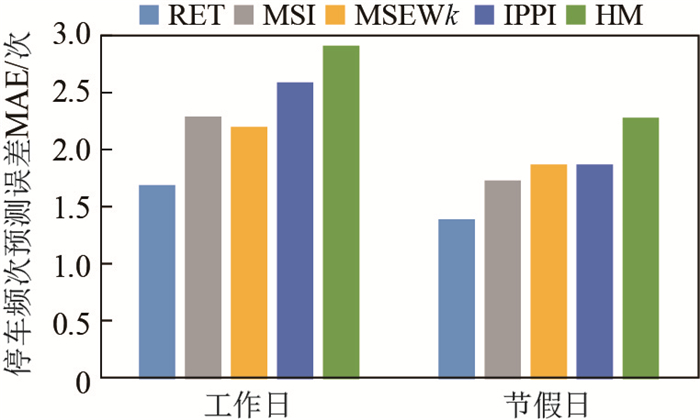
为了验证RET算法的有效性, 本文将其与当前预测用车频次/停车频次精确度较高的算法进行了对比分析, 包含基于历史数据处理的IPPI^[12]算法、HM^[8]算法和考虑多影响因素的MSI^[13]算法、MSEWk^[10]算法, 结果如图 4、图 5所示.从图 4、图 5中可以看出, 考虑多因素的算法(MSI^[13]和MSEWk^[10])在用车需求更强烈的工作日期间虽然优于传统的单因素统计预测算法(IPPI^[12]、HM^[8]), 但本文对用车频次和停车频次的时空聚类的RET算法的预测误差无论在工作日还是在节假日均低于其他算法.

RET算法是对用车点/停车点的时空聚类, 聚类效果的优劣由MinPts和$r_{\rm spatio}$值决定.比如, 首先给定MinPts值, 虽然$r_{\rm spatio}$值设置越小, 它的聚类效果越好, 但是$r_{\rm spatio}$值过小, 则会导致大量用车点、停车点被错误地标记为噪声点; 如果$r_{\rm spatio}$值设置过大, 则会将很多噪声点被错误地归入簇中.然后再给定$r_{\rm spatio}$值, 如果MinPts值设置过大, 聚类效果会很差; MinPts值设置过小, 将会使大量点被标记为核心点, 从而将噪声点错误的归入簇中.所以需要合理设置参数$r_{\rm spatio}$和MinPts.鉴于此, 本文基于实际的出租车轨迹数据进行反复调参, 最终将$r_{\rm spatio}$设置为30 m, MinPts设置为15.

4.3.2 调度优化

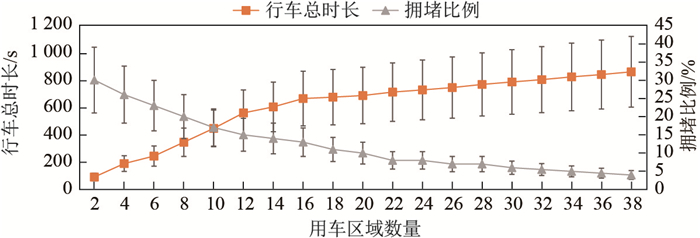
为了验证实时调度优化模型ROM方法的有效性, 本文对调度车的行车线路的效率进行了实验. 图 6呈现的是本文提出的调度优化模型ROM方法的效率图.如图 6所示, 随着用车区域数量的增加, 行车总时长增长幅度明显减弱, 拥堵比例明显减小, 最后拥堵比例保持在一个很小的范围内.即本文所提出的调度优化模型ROM方法在面对大型调度的情况下, 能明显减少行车总时长, 快速完成全部调度, 减少调度开销.

本文呈现了上海外滩区域的用车/停车区域示意图, 如图 7所示. 图 7中, 圆的大小代表用车频次或停车频次, 圆越大, 用车/停车频次越高; 红色圆表示本时段的用车区域, 蓝色圆表示上一时段的停车区域.为验证调度优化模型ROM方法的有效性和高效性, 以图 7中的用车区域$n_{4}$为例, 首先搜索距离$n_{4}$最近的top-$k$停车区域.

接着根据表 3所示的数据, 获取邻近用车区域$n_{4}$且满足用车比例(经计算为4%)的停车区域, 包括$g_{5}$、$g_{40}$、$g_{10}$、$g_{20}$、$g_{8}$.

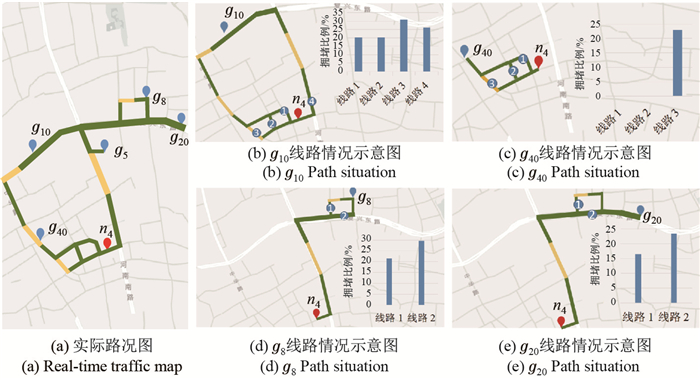
最后结合OCluST算法^[16]获取的实时路况向调度车推荐, 各停车区域到用车区域的交通状况如图 8所示.在图 8中, 通过ROM方法得到$g_{10}$到$n_{4}$的推荐行车线路为线路1和线路2; $g_{40}$到$n_{4}$推荐行车线路为线路1; $g_{8}$到$n_{4}$的推荐行车线路为线路1; $g_{20}$同$g_{8}$一样, 推荐线路也是线路1; $g_{5}$到$n_{4}$只有1条线路, 无需对比分析.

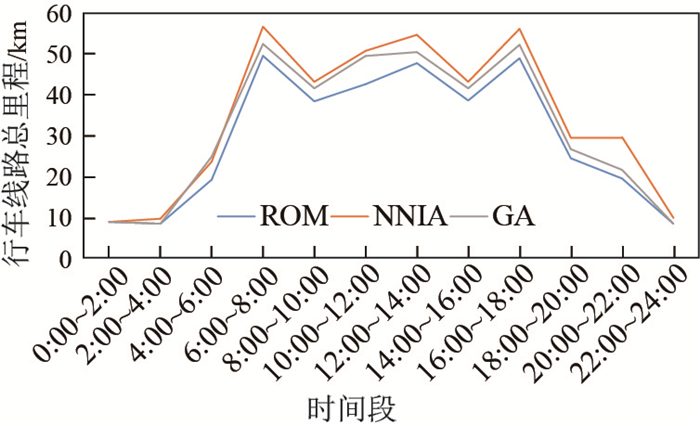
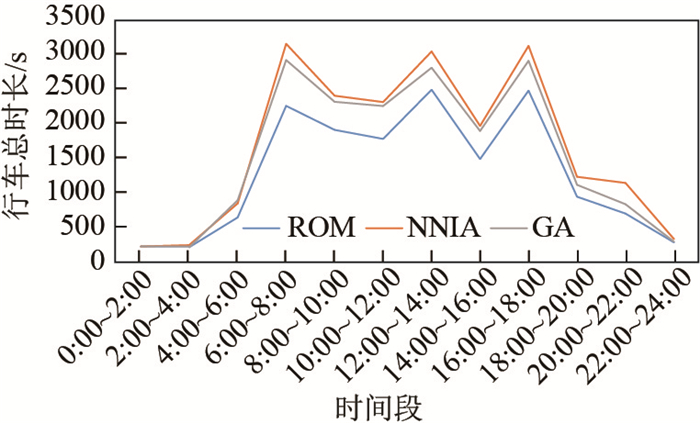
接下来将本文所提的ROM方法同其他调度优化方法NNIA^[16]和GA^[17]作对比, 图 9、图 10展示了对比结果, 测试的范围为上海外滩区域, 对42个用车区域进行投放和对35个停车区域进行调度, 优化后各时段的行车线路总里程(TMR)、行车总时长(TDT).从本文的案例研究中可以看出.本文提出的调度优化模型ROM方法在各时段都比NNIA^[16]和GA^[17]的行车线路总里程更小, 并且完成行车总时长更短, 尤其是在用车高峰时段(6:00~16:00)最为明显.本文所提的ROM方法首先是寻找距离相关用车区域最短的top-$k$停车区域, 这使得本文在行车线路的距离上最短, 所以TMR值会是最优的; NNIA^[16]和GA^[17]的TDT值之所以大, 是因为它们没有结合实时路况对行车线路进行分析, 而本文提出的ROM方法结合了实时路况, 能获取路况最好的调度车的行车线路, 所以ROM方法的TDT值更低, 尤其是用车高峰时段最为明显.

本文提出的两阶段的框架在预估城市用车需求和共享单车停车情况上, 同考虑多因素的算法(MSI^[13], MSEWK^[10])和历史数据统计预测算法(IPPI^[12], HM^[8])作对比, 通过RET算法, 首次预测出城市热门用车区域、共享单车停车区域的变化情况, 并能找到各时段内热门用车区域和停车区域的范围和位置, 且本文所提的RET算法在预估各时段内用车频次、停车频次的精确度上更高.本文所提的ROM方法同NNIA^[16]和GA^[17], 在调度优化上进行了有效性对比实验, 实验结果证明了本文所提的ROM方法在各时段的调度过程中, TMR和TDT值都更小, 即ROM方法能以较短的线路总里程和较短行车总时长的方式完成所有调度.

5 结语

为满足不同时段的城市共享单车用车需求, 本文提出了一个两阶段的共享单车实时投放及调度的框架, 该框架能准确预测各时段的用车需求及单车分布情况, 并可结合实时路况推荐调度车的较优行车线路.基于出租车数据集上的实验结果表明, 本文的RET算法能精确地预测用车需求、发现停车区域; 本文的ROM方法能有效提升调度效率.在未来的工作中, 拟结合包括天气、日期、POI数据等提取多源外部特征, 采用深度学习模型对轨迹数据与外部特征进行统一建模, 进一步提升城市共享单车的动态调度策略的高效性.