0 引言

机器博弈一直是人工智能领域的热点问题.自2016年谷歌公司研制出的"阿尔法围棋"挑战人类世界冠军李世石成功后^[1], 博弈类人工智能吸引了更加广泛和热烈的关注.不围棋, 是十多年前开始的一项博弈类游戏, 和围棋有相似之处, 比如都使用相同的棋子并且有一些相似的概念如"气"、"眼"等, 但与围棋是以最后双方所围交叉点数来判断输赢完全不同.在不围棋中, 如果一方提掉另一方的子或者是选择放弃落子, 则被判负.因此, 不围棋在输赢策略上就有了完全不同的思维方式, 而不围棋人工智能与围棋人工智能的思路也就有所不同.

针对以上问题, 本文提出了使用基于价值评估的递归算法来实现不围棋人工智能.通过利用价值评估模型和函数来对当前局面选出候选点, 之后使用递归来确定最优解.本文在接下来的组织结构是:第1节介绍不围棋及其规则; 第2节介绍目前关于不围棋人工智能的实现算法和主要缺点; 第3节给出本文的主要工作, 包括对不围棋博弈的思考、价值评估函数的构建, 以及基于价值评估的递归算法的具体思路和步骤等; 第4节给出实验结果, 包括与开源软件OASE-NoGo的对弈图和与传统算法在程序计算上的对比; 第5节对全文进行总结.

1 不围棋及其规则

不围棋使用9$\times $9棋盘, 黑棋先行, 之后黑白交替落子, 对弈中禁止自杀, 如果一方吃掉另一方的子或者是选择Pass则被判负.吃子规则与围棋相同, 就是指某种颜色的一个子或者一串棋子在棋盘上, 与它直线紧邻的交叉点为它的"气", 若所有的气都被另一种颜色占据, 则被吃掉.

2011年起, 国际计算机奥林匹克大赛增加了不围棋项目; 2012年起, 由中国人工智能学会举办的全国机器博弈大赛中也把不围棋列入竞赛项目.由此, 不围棋人工智能开始被大家所研究.

2 不围棋人工智能研究现状 2.1 研究历程

计算机博弈, 就是希望计算机像人类一样, 学习并实现博弈功能.简而言之, 就是希望计算机拥有类似人一样准确的思维、判断和推理决策能力. 1996年, 由几名国际特级大师和电脑专组成的"深蓝"国际象棋小组研究开发出的"Deeper Blue"^[2], 以3.5:2.5击败了世界冠军卡斯帕洛夫.而围棋项目, 则直到2016年才被谷歌公司用深度学习和树搜索的结合方法攻克.在这期间, 蒙特卡洛思想的UCT(Upper Confidence Bound Apply to Tree)算法曾一度在围棋人工智能领域主导了近十年的时间.文献[3-5]等都是从不同思路优化UCT算法, 来提高博弈树的搜索速度.

不围棋, 作为一种由围棋发展而来的棋种, 其人工智能的研究, 在之前的工作中, 绝大部分都是采用与围棋类似的蒙特卡洛树搜索(The Monte-Carlo Search Tree, MCTS)算法来解决.最早关于不围棋人工智能的研究出现于2011年^[6], 通过对比围棋, 发现快速评估、MCTS等方法同样适用于不围棋.与之类似的文献[7]和文献[8], 都是利用MCTS来解决不围棋问题, 其中文献[7]在选点过程中使用了和围棋相似的模式匹配方式, 一定程度上优化了使用MCTS造成的巨大的搜索空间的问题; 文献[8]则在启动MCTS算法时, 优先对评分较高的局面进行模拟, 通过这种方法来尽可能减少模拟次数.

2.2 MCTS算法及其不足之处

MCTS是一种动态评估方法, 更多的是利用数学统计中概率的思想.具体来说, 就是对问题领域内的所有可选情况, 通过不断反复地进行大量抽样, 最终所得结果会在解空间上形成一个分布, 而这个分布是接近真实的, 进而就能够得到所需的最优解或近似的最优解.

MCTS方法主要包括以下4个方面的内容.

(1) 搜索:从博弈树的根节点(即终局状态)向下搜索直至当前的叶子结点(即当前局面).

(2) 扩展:对当前的博弈树叶子结点进行扩展.

(3) 模拟:从当前的博弈树叶子结点开始进行蒙特卡洛概率模拟并给出一个蒙特卡洛概率统计数值.

(4) 更新:把蒙特卡洛模拟的结果更新到搜索过程中博弈树的每一个节点上.

之后, 重新从(1)开始, 不断反复地进行迭代, 使得添加的局面越来越多, 则对于博弈树中所有的子节点的胜利率也越来越准.最后, 选择胜利率最高的选点.因此, 怎样对蒙特卡洛中博弈树进行剪枝和如何提供准确侯选点成为难题, 在这种情况下, 利用模式匹配等方式成为主流^[9], 或标记出不能落子的点来缩小搜索范围^[10], 但以上的方法依旧不能改变蒙特卡洛思想需要大量随机模拟的事实, 无法克服蒙特卡洛思想本身的时间、空间复杂度高的问题.所以MCTS算法实现的程序就会对硬件水平、时间等提出较高要求, 不适用于硬件水平较低或反应速度要求较快的软件中.

为解决以上问题, 本文没有选择主流的MCTS算法, 而是利用不围棋博弈本身的特点, 构建了价值评估模型和函数, 通过递归的方法来实现不围棋人工智能, 并达到了与之前研究相同的棋力效果, 克服了MCTS计算复杂的问题.

3 基于价值评估的递归算法 3.1 不围棋行棋思路及价值评估函数的构建

为了避免蒙特卡洛思想本身的弊端, 本文选择用价值评估模型来实现不围棋人工智能, 主要是从不围棋本身的博弈思路来考虑.为了达到不输掉比赛的目的, 就是努力不吃掉对手的子, 那么, 就会有两种行棋思路:第一, 使自己的"气"比对手的少; 第二, 使自己的"眼"比对手的多.

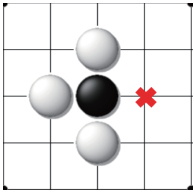
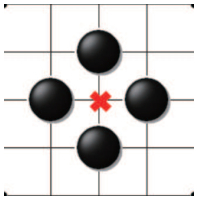
基于以上两点, 本文将被对方打吃的子数与己方"眼"的个数规定为权利数, 以此来构造不围棋的价值评估模型和函数.显而易见, 在后盘, 双方都在消耗自己的权利, 而权利数多的一方将取得胜利, 因此, 不围棋行棋的主要目的可以描述为制造己方权利或是破坏对方权利.本文中将权利的制造和破坏称为权利规则, 这一规则容易想到的方法是把各种棋形摆出来, 比如被打吃、"眼"等等.但在实际局面中, 形成权利的棋形千奇百怪, 远不是能够一一列举的.如果用模式库的方式, 则难以避免占用空间较多的问题.所以, 本文利用"气"这一概念来思考, 形成权利值的标志就是会在棋子周围的点中形成一个或多个对手无法落子的交叉点, 即这个交叉点是己方的单个眼位或己方在此处有且仅有最后一口气(如图 1和图 2中标记处), 则这个交叉点就是自己的权利.

由此, 在不围棋9$\times $9棋盘中, 记坐标点为(1, 1)至(9, 9), 从(1, 1)起, 对于第$j$个交叉点(1$\le j\le $81), 其坐标为($m$, $n)$(1$\le m\le $9, 1$\le n\le $9), 假定对于第$i$手(1$\le i\le $81)行棋颜色为黑, 在坐标($m$, $n)$处白方出现无法落子的情况, 即($m$, $n)$为黑方眼位或($m $, $n)$处为黑方棋子或棋串的最后一口气, 则记为$N_{w}$(不能落子记为1, 可以落子记为0).其此时黑方权利值$B_{i}$可以评估为

$ \begin{equation} \label{eq1} \mathop B\nolimits_i =\sum\limits_{j=1}^{81} {\mathop N\nolimits_w^j }. \end{equation} $

(1)

同理, 设第$i$手为白方, 黑方无法落子记为$N_{b}$(不能落子记为1, 可以落子记为0), 则此时白方权利值$W_{i }$可以评估为

$ \begin{equation} \label{eq2} \mathop W\nolimits_i =\sum\limits_{j=1}^{81} {\mathop N\nolimits_b^j }. \end{equation} $

(2)

对于特定局面的价值评估模型得以构建, 当进行到第$i$手时将局面总权利值记为$P_{i}$, 则

$ \begin{equation} \label{eq3} P_i =B_i +W_i. \end{equation} $

(3)

在不围棋行棋过程中, 黑白颜色的不同并不会影响当前局面的价值, 也就是说, 某一选点的优劣不会因当前行棋颜色不同而不同.因此, 无论黑白哪方在进行到第$i$手(1$\le i\le $81)时, 只要选择$P_{i}$最大的点落子即可.因此, 可得出某一点($p$, $q)$的价值$V$的评估函数为

$ \begin{equation} \label{eq4} V(p, q)=\sum\limits_{j=1}^{81} {\mathop N\nolimits_w^j } +\sum\limits_{j=1}^{81} {\mathop N\nolimits_b^j }. \end{equation} $

(4)

根据式(4), 可以对当前局面下所有可下点计算价值, 其评估函数的伪代码如下.

Valuepoint(选点, 手数$i)$

{

  将此选点模拟为黑棋;

  While(81个点均被遍历)

  {

    检测当前所有白棋不可落子的地方, 记为$a$;

    则黑棋权利值$P_{b}$$\leftarrow $a-i;

  }

  将此选点模拟为白棋;

  While(81个点均被遍历)

  {

    检测当前所有黑棋不可落子的地方, 记为$b$;

    则白棋的权利值$P_{w}$$\leftarrow $b-i;

  }

此点评估价值为$P=P_{b}+P_{w}$;

Return $P$;

}

3.2 基于价值评估的递归算法

由第3.1节中得到的评估函数可以评价任意局面中任一交叉点的价值, 且此价值与当前行棋的颜色无关, 若只有一个最高价值的点, 则此点为最佳选点.但在执行过程中, 由于局面的复杂性, 经常会遇到一个问题, 就是在某一局面下会出现不只一个使式(4)中$V$最大的点.因此, 为了解决这个问题, 也为了找到最优解, 本文采用递归的算法来完善价值评估思路.特别地, 当所有点的价值在递归(一般选用三层)之后, 计算结果仍均为0, 本文将采用打散规则来处理.

3.2.1 打散规则

在不围棋中, 有时会出现递归三层的价值评估最大值都相同的情况.典型的例子就是开局阶段, 经常会出现选点没有优劣之分的情况.在这种情况中, 可以选择随机落子来解决问题, 这并不会过多地影响人工智能的整体水平.但在本文中, 基于对不围棋的大量实践和博弈特点的思考, 选择使用打散规则来代替随机落子, 作为对不围棋开局的一种优化, 且当棋盘为空时, 算法中选择最中心, 即天元点作为开局.

在打散规则中选择曼哈顿距离$d(i$, $j)$, 且

$ \begin{equation} d(i, j)=\vert X_1-X_2\vert +\vert Y_1-Y_2\vert, \end{equation} $

(5)

即两个点在标准坐标系上的绝对轴距总和来进行打散, 使行棋打散程度最大化.

打散功能函数具体步骤如下.

第一步:选出所有可下点, 剔除已有子的交叉点和己方不能行棋的点, 如对方眼位或会吃掉对方棋子处.

第二步:计算所有可下点与棋盘已有子的曼哈顿距离的最小值.

第三步:找出第二步中所得最小值的最大值, 标记相应的点, 若唯一, 则确定此点为打散规则中的最优解, 若有多个, 则随机选择.

3.2.2 递归算法步骤

当出现最大评估价值包含多个交叉点时, 本文将这些交叉点设为候选点, 之后利用递归的思想对这些候选点进行多次的价值评估, 最终选取多次价值评估后出现最大值的候选点为最优解.其递归算法步骤为如下.

第一步:寻找出当前局面中价值评估为最大的所有候选点.

第二步:依次将所有候选点设置为当前行棋的棋子(黑子或白子).

第三步:更新第二步所得棋盘, 计算评估值, 若为0, 则跳出递归算法, 执行打散规则; 若非0, 则继续.

第四步:对所有候选点得到的局面进行多次价值评估, 直到有且仅有一个候选点的价值最大.

第五步:出现价值最大的情况, 则返回最初选择的候选点.

4 实验结果 4.1 功能展示

根据上述算法, 本文实现了一个不围棋人工智能软件, 在普通配置(4 GP内存, 双核)的笔记本上每一手的响应时间在2 s之内. 图 3和图 4为此软件的运行结果图, 其中图 3是与开源软件OASE-NoGo的对弈结果.

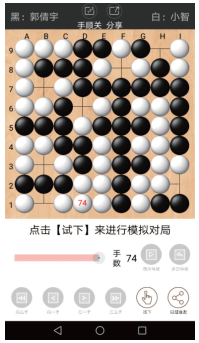
同时, 此算法实现的程序还可以在普通安卓手机上运行, 测试手机为内存3 GB, 8核, 响应时间在2 s之内.结果如图 5所示.

4.2 效果对比

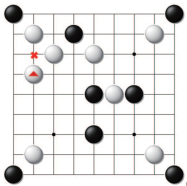
表 1是本文系统与OASE-NoGo软件的对弈结果及胜率统计, 本文的胜率均达到90%以上.针对图 6这对奕中的一常见局面, 本算法与传统蒙特卡洛算法的复杂性对比可以体现出本文算法的可行性和高效性.

文献[8]中所实现的程序与OASE-NoGo V1.1初级的对弈胜率为90%, 小于本文中程序的胜率.

复杂性对比方面, 图 6为对弈中的某一局面, 按照理论, MCTS算法在足够长的时间中才能给出标记点结果, 而本文算法在1 s内即给出与MCTS算法相同结果, 即交叉点为最佳选点.而当MCTS算法没有足够时间模拟时, 将可能不能得到此结果, 具体分析如下.

MCTS算法计算过程:当前落子颜色为黑, 可下点为65个.通过模式匹配、快速估计等方式找出3到4个候选点, 其中包括标记点.之后在规定时间内对所有候选点进行尽可能多的蒙特卡洛模拟, 一次模拟的方式为采用黑一手、白一手的交替落子方式将棋至终局, 若黑胜, 则给此候选点加特定分数, 若黑负, 则减少特定分数, 在最后时间用完时比较几个候选点的分数, 选择分数最高的点为最佳.显而易见, 此算法将消耗大量的时间空间, 且若时间不充分, 模拟次数不够, 则评分不一定准确, 不能保证得出最佳结果.

本文系统算法计算过程:可下点为65个, 对所有点进行一次价值评估计算, 即进行130次黑白是否能够落子的判断; 之后进行65次加法运算, 可得到标记处和标记出左边的交叉点价值最高, 为1, 其他点均为0;后对这两个候选点进行第二次计算, 分别将计算128次是否落子的判断和64次加法运算, 可得到标记出第二次计算的价值为1, 而标记出左边的交叉点第二次计算的价值为0.因此得出最佳结果, 运行时间为1 s之内.

5 结论

针对当前不围棋人工智能中使用蒙特卡洛思想带来的不足之处, 结合不围棋本身的博弈特点, 本文给出了全新的基于价值评估函数的递归的解决方法; 详细介绍了价值评估模型的构建和价值函数的计算过程; 针对在价值评估中会出现的多候选点问题, 提出了打散规则和使用递归这一思想, 使这一难点得以解决.以上述算法为核心的软件在实验结果中取得了较好的效果, 证明了本文算法的可行性和有效性.