2. 合肥工业大学 电气与自动化工程学院, 合肥 230009
2. School of Electrical and Automation Engineering, Hefei University of Technology, Hefei 230009, China
节点定位是无线传感网络(WSN)应用的关键技术之一.根据节点定位算法结构.节点定位分为非学习型和学习型, 后者对信标节点(已知位置节点)密度要求低且定位精度高, 目前应用较广.学习型中应用较多的多维尺度(MDS)算法是一种线性降维方法, 通过节点间欧氏距离表征节点非相似性, 将高维空间数据以图形形式在低维空间再现, 实现维数约减, 进而估计节点位置[1-6].但节点间信号受路径损耗、多径传播、环境温湿度及节点位置的随机性等因素影响[7], 节点位置信息呈现非线性关系, 高维空间中呈现扭曲, 线性降维方法难以实现维数约减, 尤其当高维数据集在欧式空间相应的子集非凸时, 数据集的低维嵌入结构还会产生较大的变形.
ISOMAP算法是在MDS算法框架基础上, 采用节点间测地距离替代欧式距离, 通过双质心变换实现算法降维的非线性扩展[8-10].但数据集中存在噪声干扰, 使得质心变换后距离矩阵无法满足半正定条件, 算法泛化能力差[11-12]. Heeyoul等学者提出了基于核矩阵的ISOMAP算法KISOMAP, 通过构建核矩阵保证距离平方矩阵的半正定性, 提高了算法泛化能力[13].但ISOMAP和KISOMAP算法均基于最小二乘法(Least Square, LS)求解, 对数据异常点敏感, 求解难易度依赖于邻域大小选择, 限制了算法稳健性和拓扑稳定性, 且样本增加时, 需重新计算全部样本测地距离, 运算复杂度呈指数增加[14].
本文基于PLS的KISOMAP(PLS-KISOMAP)节点定位算法是在ISOMAP算法基础上, 利用PLS辅助分析方法中的贡献率找寻和剔除邻域中的〝短路〞边(离群点), 提高了算法运算效率和定位精度; 通过构造核矩阵改进了算法泛化能力; 在高维特征区间里, 采用PLS求解节点相对位置, 进一步提高了其稳健性和网络拓扑性; 与经典MDS、ISOMAP和KISOMAP定位方法进行了比较, 仿真结果验证了本文所提出的PLS-KISOMAP定位算法的有效性.
1 ISOMAP节点定位算法高维空间中, 假设传感器节点集为X={X1, ..., Xm, Xm+1, ..., XN}, 其中Xi=(xi, 1, ..., xi, w)是节点i的坐标, N(N=m+n)是网络节点个数, m和n分别为网络中信标节点和未知节点数目, w为空间维度(等于2或3), 则节点i和j的欧氏距离di, j为
| $ d_{i, j} =\sqrt {\sum\limits_{k=1}^w {(x_{i, k} -x_{j, k} )^2} } =\left\| {x_i -x_j } \right\|_F , $ | (1) |
其中, ‖·‖是Frobenius范数.
考虑测量误差和噪声干扰, 则节点i和j的实际欧氏距离Ri, j为
| $ R_{i, j}=d_{i, j} +ξ _{i, j}, $ | (2) |
其中, ξi, j是噪声干扰和测量误差, 假定服从正态分布, 即ξi, j~N(0, σi, j2).
ISOMAP节点定位算法通过构造邻域图, 利用样本向量间测地距离表示节点非相似性, 通过等距映射获得高维空间观测数据集在低维空间的表示, 真实再现其内在非线性几何结构, 实现了算法的非线性扩展, 具有较高的定位精度.
ISOMAP节点定位算法步骤简要描述如下.
(1) 选取K邻域(或ε -邻域), 构造邻域图G(V, E), 其中V是传感器网络节点集合, E是边的集合.计算节点i和j的欧氏距离di, j, 如果节点i和j为邻域点, 则边的权值DG(i, j)=di, j.
(2) 计算质心化测地距离平方矩阵K.如果图G有边, 则DG(i, j)=di, j, 否则DG(i, j)=∞利用Dijkstra算法确定图G的测地距离矩阵DG, 根据希尔伯特空间理论和双质心变换方法计算
(3) 基于LS方法, 对矩阵K运用奇异值分解方法求解节点相对位置坐标.
2 基于PLS法的KISOMAP节点定位算法PLS-KISOMAP节点定位算法是在ISOMAP算法基础上, 利用PLS方法寻找和剔除邻域图中的〝短路〞边, 再根据核技术思想构建Mercer核矩阵, 最后利用PLS方法求解节点相对位置.
2.1 〝短路〞边的确定邻域大小直接决定ISOMAP算法的拓扑稳定性、鲁棒性及运算效率, 邻域过大将破坏数据集流形结构, 产生〝短路〞边, 使得邻域不能正确地表达数据集结构, 邻域过小则影响流形结构的连续性.传统ISOMAP算法邻域的确定通过预先设置邻域参数, 依靠映射〝质量〞(残差矩阵)大小判定参数选取的好坏, 运算效率低.通过寻找和剔除邻域图中的〝短路〞边, 使得算法对邻域大小不再敏感, 则可以避开邻域大小难以有效选取的问题, 提高运算效率.空间离群点检测算法有基于聚类、距离、密度和统计等类型, 当空间数据存在严重自相关性和异质性等约束条件时, 基于统计的算法具有较好的效果.
PLS方法是一种适合于回归和分类研究的第二代建模方法, 广泛运用于机器学习和化学分析等领域, 利用输入和输出向量之间的协方差信息提取数据潜在特征, 可同时实现多元线性回归、主成份分析和典型相关分析, 对样本数量要求少, 运行速度快, 易于区分有效信息和噪声, 适合于自变量存在严重多重相关性的场合[10].样本点贡献图利用样本点中各变量对解释变量空间中潜变量的贡献分析其对总趋势的影响, 可以检测出对模型影响较大的离群点, 是PLS方法特有的离群点检测技术, 具有较强的检测能力.
假设流形结构中样本点分布是一致的, 即所有样本点对数据集的潜变量贡献一致.令测地距离矩阵中样本点i中解释变量j对潜变量th的贡献率Contij, h为
| $ {\rm{Cont}}_{ij, h}=\frac{1}{s_h}D_{hi}X_{ij}, $ | (3) |
其中, sh是潜变量th的标准差
则样本点i对潜变量th (h=1, 2, ..., p)的总贡献率Contij为
| $ {\rm{Cont}}_{ij}^2 =\sum\limits_{h=1}^p {{\rm{Cont}}_{ij, h}^2 } =\sum\limits_{h=1}^p {\left( {\frac{1}{s_h }D_{hj} X_{ij} } \right)} ^2. $ | (4) |
如果Contij, h2远大于Contij2/ρ或者Contij2远大于其他样本点的总贡献率, 则认为样本点i是〝短路〞边.参照留一交叉验证法, 构造全体样本总贡献率方差矩阵CCσ(e)和删除样本点i后的样本总贡献率方差矩阵CCσ(e, -i), 两者差值为Δ CCi, 如果Δ CCi大于预先设定值, 则认为该样本点为〝短路〞边.该方法关键是如何确定合适的预先设定值, 结合偏F检验方法, 根据偏F统计量衡量样本点偏离群体的程度, 避免预先设定值的选取问题[10].
按照定义有
| $ \Delta C{C_i} = C{C_{\sigma (e)}} - C{C_{\sigma (e, - i)}}. $ | (5) |
采用ΔCCi作为衡量样本点i与其他样本点贡献率的偏差程度的统计量, 构造偏F统计量
| $ {F_i} = \frac{{\Delta C{C_i}}}{{{\sigma ^2}}} = \frac{{C{C_{\sigma (e)}} - C{C_{\sigma (e, - i)}}}}{{C{C_{\sigma (e)}}/(n - p - 1)}}. $ | (6) |
即统计量Fi服从F(1, n-p-1)分布, 如果Fi≥F(1, n-p-1), 则认为样本点i为〝短路〞边.
2.2 核矩阵的构建ISOMAP算法是通过非线性映射将给定空间内的线性不可分问题在相应高维特征空间内转换为线性可分问题, 但存在非线性映射形式选择及特征空间维数等问题, 维数较高时会产生运算〝维数灾难〞.根据希尔伯特空间理论(希尔伯特空间下正定核函数存在和判定的充分必要条件), K需满足Mercer条件, 为半正定矩阵, 由于噪声影响及测地距离近似性, K无法保证其正定性, 算法泛化能力差.
核技术就是利用核函数替代非线性映射中的内积运算, 避免映射形式选择和〝维数灾难〞问题. ISOMAP算法被视为核主成分分析(Principal Component Analysis, PCA)方法, 采用增加常量的方法将K变换为Mercer核矩阵, 可以同时保证测地距离的不变性及的半正定性, 利用核矩阵的对角化获得高维数据的低维嵌入, 提高算法的泛化能力[9].
令c*为矩阵
| $ \widetilde{D}_{ij}=D_{ij}+c(1-δ_{ij}), $ | (7) |
其中, δij是Kronecker delta函数.
经过双质心变换, K相应的Mercer核矩阵
| $ \widetilde{K}=K(\widetilde{D}^2)+2cK(\widetilde{D})+\frac{1}{2}c^2H. $ | (8) |
根据Mercer核矩阵定义,
| $ \widetilde{K}=k(x_i, x_j)=Φ^{\rm{T}} (x_i)Φ(x_j), $ | (9) |
其中, Φ(·)为非线性映射形式.
2.3 节点相对位置求解从第2.2节可以看出, ISOMAP节点定位算法可以表述为最优化问题
| $ \min\limits_{D^*∈ {\rm{EDM}}}\|K-K^*\|_F^2 , $ | (10) |
其中, EDM为测地距离矩阵集, K*为K相应的低维空间重构矩阵.
式(10)实质就是利用LS方法求解半定规划(Semi-Definite Programming, SDP)问题[10], 通常采用矩阵奇异值分解方法.高维特征空间里, N个样本点的协方差矩阵为
| $ C=\frac{1}{N}Φ(H)Φ^{\rm{T}}(H). $ | (11) |
对协方差矩阵C做特征值分解, 并对相应的特征向量矩阵做归一化处理, 便得到样本点在的特征空间里的相对位置坐标.
假设DG中测量误差和噪声干扰服从高斯分布, 经过双质心变换, 根据式(7)、式(8)、式(9), 核矩阵
| $ \begin{array}{l} {{\tilde K}_{ij}} = - \frac{1}{2}(\tilde D_{ij}^2 - {{\tilde K}_{jj}} - \frac{1}{n}\sum\limits_{i = 1}^n {\tilde D_{ij}^2} - {{\tilde K}_{ii}})\\ \;\;\;\; = \frac{{n - 1}}{n}R_{i,j}^2 - \frac{{n - 1}}{{{n^2}}}\left( {\sum\limits_{i = 1}^n {R_{i,j}^2} + \sum\limits_{j = 1}^n {R_{i,j}^2} } \right) + {\left( {\frac{{n - 1}}{n}} \right)^2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {R_{i,j}^2} } . \end{array} $ | (12) |
从式(12)可以看出, 矩阵
采用PLS方法求解式(10)时, 则可以表述为最优化问题
| $ \left\{ \begin{array}{l} \max :{\rm{Tr\{ }}{U^{\rm{T}}}CV\} ,\\ {\rm{约束条件}}:{U^{\rm{T}}}U = {V^{\rm{T}}}V = I, \end{array} \right. $ | (13) |
其中, U和V分别为高维特征(对偶)空间的特征向量矩阵.
PLS-KISOMAP算法中, 回归模型中输入矩阵X为核矩阵
| $ \left\{ \begin{array}{l} \max :{\rm{Tr\{ }}{U^{\rm{T}}}{\Phi ^{\rm{T}}}K^*V\} ,\\ {\rm{约束条件}}:{U^{\rm{T}}}U = {V^{\rm{T}}}V = I. \end{array} \right. $ | (14) |
PLS方法采取非参数估计方法, 避免了LS方法严格要求参数问题, 对样本数据无分布要求, 均能得到渐进正确的估计. PLS-KISOMAP算法结合了PLS和核技术的优点, 实现了PLS线性回归到高维非线性空间的延伸, 同时回归模型中输入矩阵为质心矩阵, 消除了偏置项影响, 减少了回归系数矩阵维数及计算复杂度.
2.4 新增样本点的处理样本维数为l, 个数为N时, ISOMAP算法的计算复杂度为O(lN2)[8-9]; 而样本增加时, ISOMAP算法通过合并全部数据集后重新学习获取其低维流形结构, 则算法计算时间成指数倍增加, 学习效率低, 限制了样本集规模.
根据核矩阵特征向量求解方法, 新增样本点xl的低维向量为
| $ [y_l]_i=\frac{1}{\sqrt{λ_i}}\sum\limits_{j=1}^N[v_i]_j· k(x_l, x_j), $ | (15) |
其中, λi 表示
| $ \widetilde{D}_{lj}^2=[\phi (x_l)-\phi(x_j)]^{\rm{T}}[\phi(x_l)-\phi(x_j)]. $ | (16) |
根据式(8)、式(11)有
| $ \frac{1}{N}\sum\limits_{j=1}^N\widetilde{D}_{lj}^2=\phi^{\rm{T}} (x_l)\phi(x_l)+\frac{1}{N}\sum\limits_{j=1}^N\phi^{\rm{T}}(x_j)\phi(x_j). $ | (17) |
则xl与xj的测地距离为
| $ k(x_l, x_j)=-\frac{1}{2}\Big(\widetilde{D}_{lj}^2-\widetilde{K}_{jj}-\frac{1}{N} \sum\limits_{i=1 }^N\widetilde{D}_{lj}^2-\widetilde{K}_{ii}\Big). $ | (18) |
按照矩阵分块思想, 则式(14)可以表示为
| $ \left\{ \begin{array}{l} \max :{\rm{Tr\{ }}{U^{\rm{T}}}{\Phi ^{\rm{T}}}{\left( \begin{array}{l} {K_{{\rm{new}}}}\\ K \end{array} \right)^*}V\} ,\\ {\rm{约束条件}}:{U^{\rm{T}}}U = {V^{\rm{T}}}V = I. \end{array} \right. $ | (19) |
其中, Knew表示新增样本与原样本的测地距离矩阵.
从式(18)、式(19)可以看出, 当新增样本时, 只需计算xl与原样本的测地距离矩阵, 而K*可以直接运用, 减小了计算量.
3 仿真实验为验证本文算法的有效性, 将PLS-KISOMAP节点定位方法与经典MDS、ISOMAP和KISOMAP定位方法进行对比.假设传感器网络节点部署在10 m× 10 m× 2 m空间内, 网络全连通.
实验中, 定位算法性能评价采用平均定位误差作为评价指标[1-2], 为
| $ E_r=\frac{\sum\limits_{i=m+1}^N\|x_{e, i}-x_{r, i}\|^2_F}{(N-m)× r}× 100%, $ | (20) |
其中, r是节点通信半径, xe, i和xr, i分别是节点i的估计位置和实际位置.实验中, 参数m=10, r取定值2 m.
图 1为节点规则部署且位于同一平面网络拓扑结构时, 经典MDS、ISOMAP、KISOMAP和PLS-KISOMAP算法的定位误差曲线.从图 1看出, 随着采样次数增加, 从网络结构中获取的有关距离信息越多, 经典MDS算法中重构的相似性矩阵误差越小, ISOMAP算法及其改进算法中最短路径距离替代欧式距离的精度越高, 4种算法的定位误差均呈现下降趋势. ISOMAP与MDS算法基本框架一致, 当节点为规则平面网络结构时, 节点间测地距离近似于欧氏距离, ISOMAP退化成MDS算法.因此4种算法定位误差相差不大, 彼此差异主要来源于LS和PLS方法求解SDP问题的解偏差.
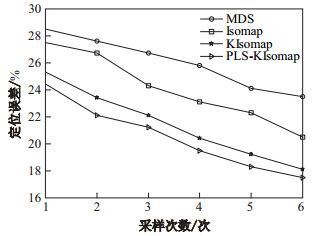
|
图 1 节点平面布置场景下定位误差曲线 Fig.1 The localization error curve in plane layout |
图 2和图 3为节点网络部署在鞍形曲面上时, MDS、ISOMAP、KISOMAP和PLS- KISOMAP算法的定位效果, 图中〝○〞、〝▲〞、〝+〞和〝*〞分别表示~MDS、ISOMAP、KISOMAP和~PLS-KISOMAP节点估计位置, 〝□〞表示节点实际位置. MDS平均定位误差为34.2%, 最大误差达到43.5%; ISOMAP平均定位误差为28.8%, 最大误差为32.6%; KISOMAP平均定位误差为22.8%, 最大误差为32.7%; PLS-KISOMAP平均定位误差为17.8%, 最大误差为26.6%.结果表明, 当节点部署在曲面上时, MDS算法只能寻找节点间的线性关系, 而ISOMAP、KISOMAP和PLS-KISOMAP算法可以发现节点间的非线性关系, 因而后3者定位效果要优于前者.在曲面图形的边沿位置, 由于获取的有关节点位置信息较少, 定位效果相对较差.同时, PLS-KISOMAP算法利用PLS辅助分析方法中的贡献率找寻和剔除邻域中的〝短路〞边, 提高了算法定位精度.
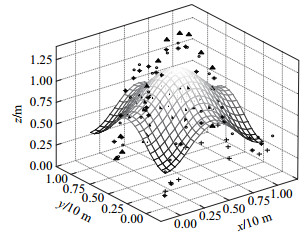
|
图 2 节点曲面布置场景下定位效果三维图 Fig.2 3D diagram of the localization effect curve plane |
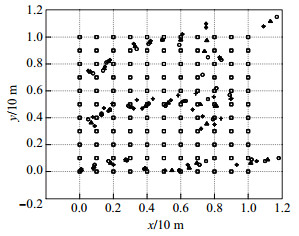
|
图 3 定位效果X-Y面投影图 Fig.3 The X-Y plane projection diagram of localization effect |
图 4为噪声水平改变情况下, 经典MDS、ISOMAP、KISOMAP和PLS-KISOMAP这4种算法的定位误差比较结果.可以看出, 4种算法定位误差均随着噪声水平增大而增加, PLS-KISOMAP、KISOMAP和ISOMAP算法较MDS误差增加趋势缓慢.同样噪声条件下, PLS-KISOMAP算法通过剔除样本集中的特异点, 减少了噪声影响, 同时采用PLS方法提高了求解精确度, 误差最小且变化相对平稳. 图 5为节点定位算法执行时间与样本数目的关系.从图 5中看出, 样本增加时, MDS、ISOMAP和KISOMAP算法需要对包括原样本集的整个新样本集进行重新计算, 而PLS-KISOMAP算法只需计算新增样本与原始样本之间的测地距离, 减少了计算复杂度, 算法执行速度快.当样本个数大于350时, 四种算法的执行时间均急剧增加, 是因为MDS、ISOMAP、KISOMAP和~PLS-KISOMAP算法是将定位问题转化成SDP问题, 而SDP的算法复杂度高, 当样本数量较大时, SDP~算法执行时间较长.

|
图 4 噪声对定位误差的影响 Fig.4 The effect of noise on localization error |
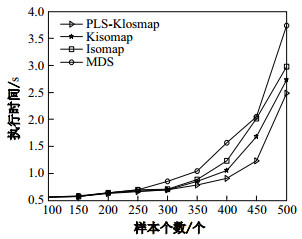
|
图 5 算法定位时间比较 Fig.5 Comparison of localization time |
本文提出了一种PLS-KISOMAP节点定位算法, 有效利用了ISOMAP保持数据集全局结构的特性; 通过PLS方法中的样本点贡献率寻找并剔除邻域中的〝短路〞边, 避免了ISOMAP算法中邻域大小选择困难问题; 利用PLS方法对样本分布不敏感和核矩阵的半正定性特点, 运用PLS求解节点位置坐标, 降低了噪声分布形式变化对算法影响, 提高了算法泛化能力和求解精度; 基于分块核思想求解新增样本点, 进一步提高了算法运行速度. PLS-KISOMAP节点定位算法是在MDS算法框架基础上发展而成的一种非线性降维学习方法, 适合于全部MDS节点定位算法应用场合, 同时适应于凸区域和非凸区域.本文研究中假定节点通信半径为定值, 而实际网络中, 由于环境影响及传感器自身性能差异, 网络中节点通信半径存在差异, 影响着算法定位效果.下一步工作将研究节点通信半径改变及节点位置移动时的定位问题.
| [1] |
丁英, 孙雨耕, 李婷雪. 基于多维校正的无线传感器网络多维标度定位算法[J]. 仪器仪表学报, 2009, 30(5): 1002-1011. DOI:10.3321/j.issn:0254-3087.2009.05.020 |
| [2] |
KUMAR S, KUMAR R, RAJAWAT K. Cooperative localization of mobile networks via velocity-assisted multidimensional scaling[J]. IEEE Transactions on Signal Processing, 2016, 64(7): 1744-1758. DOI:10.1109/TSP.2015.2507548 |
| [3] |
郝志凯, 王硕, 谭民. 基于优化策略的混合定位算法[J]. 自动化学报, 2010(5): 711-719. |
| [4] |
叶飞虎, 白光伟, 沈航. 无线传感器网络距离自调整的MDS定位算法[J]. 计算机科学, 2012(5): 40-43. DOI:10.3969/j.issn.1002-137X.2012.05.008 |
| [5] |
CUI W, WU C D, MENG Wi, et al. Dynamic multidimensional scaling algorithm for 3-D mobile localization[J]. IEEE Transactions on Instrument and Measurement, 2016, 65(12): 2853-2865. DOI:10.1109/TIM.2016.2608518 |
| [6] |
MANDANAS F D, KOTROPOULOS C L. robust multidimensional scaling using a maximum correntropy criterion[J]. IEEE Transactions on Signal Processing, 2017, 65(4): 919-932. DOI:10.1109/TSP.2016.2625265 |
| [7] |
ZHAO Y, CHENG H W, YI D Y, et al. Initial state estimation for boost phase object based on linear least square estimation[J]. Journal of Electronics and Information Technology, 2010, 32(12): 2884-2889. |
| [8] |
TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290: 2319-2323. DOI:10.1126/science.290.5500.2319 |
| [9] |
ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290: 2323-2326. DOI:10.1126/science.290.5500.2323 |
| [10] |
LAW M H C, JAIN A K. Incremental nonlinear dimensionality reduction by manifold learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(3): 377-391. DOI:10.1109/TPAMI.2006.56 |
| [11] |
邓文莲. 无线传感器网络节点定位的仿真研究[J]. 计算机仿真, 2012(5): 56-73. |
| [12] |
陈璋鑫, 宋玉梅, 万群. LAD准则下的无线传感器网络节点定位方法[J]. 电子科技大学学报, 2009, 38(1): 43-46. |
| [13] |
CHOI H, KATAKE A, CHOI S, et al. Alpha-integration of multiple evidence[C]//2010 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2010: 2210-2213.
|
| [14] |
LI B, HE Y G, GUO F M, et al. A novel localization algorithm based on isomap and partial least squares for wireless sensor networks[J]. IEEE Transactions on Instrument and Measurement, 2013, 62(2): 304-314. DOI:10.1109/TIM.2012.2216476 |




