Networks provide a mathematical structure for the analysis of natural and man-made systems. We need networks in scientific communities and they exist in nature in many complex systems; these system can be represented as random graphs or directed networks[1] where the nodes are the components that represent the system, while the edges link connecting elements and stand for the interactions between the nodes. Typical examples include river networks, scientific collaboration networks, highway networks, the worldwide airport network, metabolic networks, etc[2-6]. A fractal network is a geometric form which is self-similar and has fractional dimension. Meifeng Dai et al. introduced the box dimension of weighted fractal networks[7-8].
Recently, fractals have attracted growing attention in mathematics, physics, and other scientific studies. Biologists use them in examining certain dynamical diseases, and mathematicians use them in research projects, owing to the striking beauty intrinsic in their structures and the increasing impact of the fractals concept. Hence, it is important to combine weighted networks with the fractals concept, which we refer to hereinafter as weighted fractal networks[9-10]. In [11], the concept of mean first-passage time on a Koch network was proposed. Long Li et al. studied the scaling of mean first-passage time of a family of small-world treelike networks created by two parameters[12]. Inspired by Koch fractals, researchers proposed a family of actual networks called Koch networks and weighted tetrahedron Koch networks[13-15].
Motivated by airport networks, metabolic networks, and by the recursive division method[16], we construct the recursive homogeneous and non-homogeneous weighted Koch networks in which each edge's weight in every triangle depends on the scaling factor t∈
(0, 1) for homogeneous model and on different scaling factors t, s
∈ (0, 1) or t, r, s ∈ (0, 1) for the non-homogeneous model. In this paper, random walk on a family of homogeneous and non-homogeneous weighted Koch networks was studied. Based on the definition of the average weighted longest path (AWLP), we define the average weighted receiving time (AWRT). In this model, the walker at each step starts from its beginning node and moves uniformly to one of its neighbors. Moreover, the AWLP, in the infinite limit of the network order, only depends on the sum of scaling factors t, r, s∈(0, 1). We should mention that we only study a specific family of non-homogenous fractal hierarchical structures and non-homogenous weighted Koch networks, as mentioned by Meifeng Dai et al. in [17-18]. Our results show that in a large network, the AWRT grows as a constant of the network order when the k-th generation goes to infinity, represented by
In this section, our goal is to construct recursive homogeneous weighted Koch networks. In these networks, the topology of every equilateral triangle has the same weight on its three edges. For convenience, we describe the model using the recursive division method to define recursive homogeneous weighted Koch networks. Let us fix a positive real number t∈ (0, 1), such that the steps of constructing recursive homogeneous weighted Koch networks for all generations k=0, 1, 2, 3, ..., n-1, n, n+1 are as follows.
Step 1 Given an initial network G(0) (i.e., G0), G0 consists of three merging nodes L0={pi:i=1, 2, 3} and three edges linking these nodes with a unit weight forming equilateral triangle as shown in Figure 1.
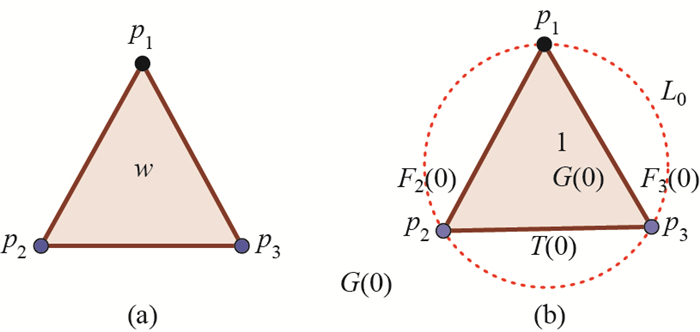
|
图 1 (a) w represents three edges with weight w in a triangle; (b) G0 (i.e., G(0)) with w=1 Fig.1 (a) w represents three edges with weight w in a triangle; (b) G0 (i.e., G(0)) with w=1 |
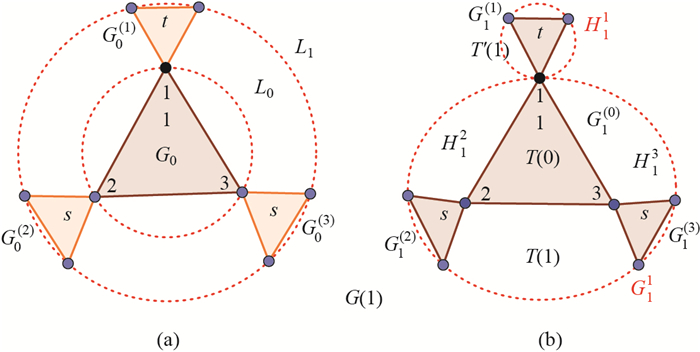
Step 2 Let G0(i), i=1, 2, 3, be three copies of G0, whose weighted edges have been scaled by a factor 0 < t < 1. Let us denote by {pii:i=1, 2, 3}, the node in G0(i) that is the image of the node initially labeled pi ∈ G0. G(1) is obtained by amalgamating three copies G0(i), i=1, 2, 3, and G0 by merging three pairs of pii and pi, i=1, 2, 3, respectively, into a new single node which are then the merging nodes {pi:i=1, 2, 3} ({1, 2, 3} for short) of G(1), as shown in Figure 2(a).
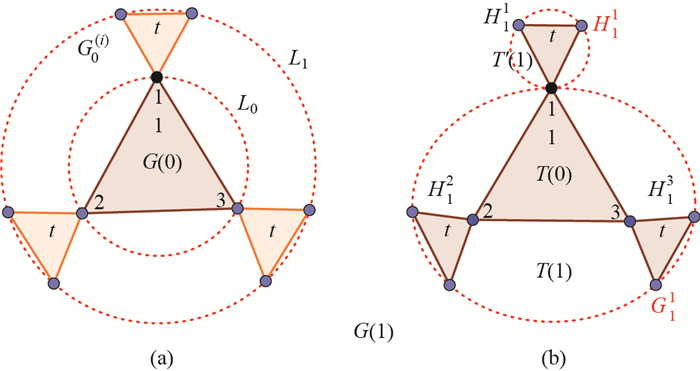
|
图 2 (a) The construction of G(1) as layers; (b) G(1) is regarded as the merging of H11 and G11 Fig.2 (a) The construction of G(1) as layers; (b) G(1) is regarded as the merging of H11 and G11 |
For the convenience of constructing of G(2), G(1) can be regarded as the merging of H1i and G1i, i=1, 2, 3, whose connection nodes are {1, 2, 3}, respectively, as shown in Figure 2(b). From the self-similarity of G(1), G(1) can be regarded as four groups, sequentially denoted as G1(0), G1(1), G1(2) and G1(3).
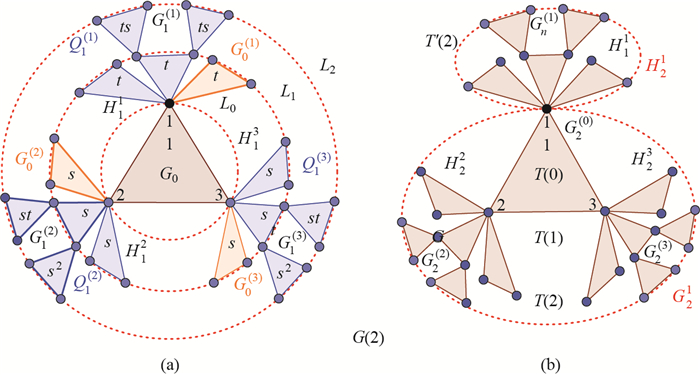
Step 3 Let G1(i) be the copy of G1i, i=1, 2, 3, whose weighted edges have been scaled by a factor 0 < t < 1, and let Q1(i)=G1(i)∪ H1i, i=1, 2, 3, where G1(i)∩ H1i={pii, i=1, 2, 3, {pii:i=1, 2, 3} is the image of the initially labeled node {pi:i=1, 2, 3}. G(2) is obtained by amalgamating three groups Q1(i), i=1, 2, 3, and G(1) by merging three pairs of pii ∈ Q1(i) and pi ∈ G(1), i=1, 2, 3, respectively, into a new single node which are then the merging nodes {pi:i=1, 2, 3} ({1, 2, 3} for short) of G(2), as shown in Figure 3(a).
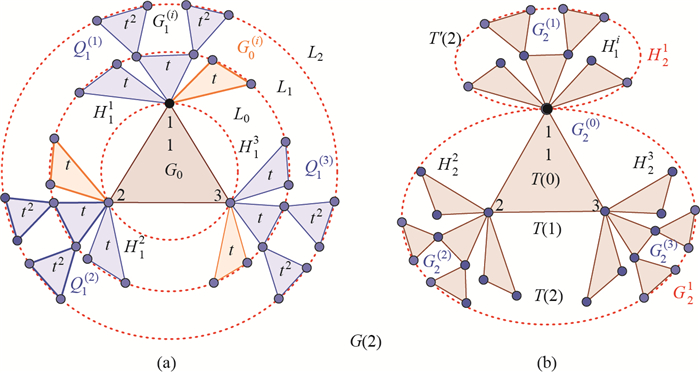
|
图 3 (a) The construction of G(2) as layers; (b) G(2) is regarded as the merging of H21 and G21 Fig.3 (a) The construction of G(2) as layers; (b) G(2) is regarded as the merging of H21 and G21 |
For the convenience of construction of G(3), G(2) can also be regarded as the merging of H2i and G2i, i=1, 2, 3, whose connection nodes are {1, 2, 3}, respectively, as shown in Figure 3(b). From the self-similarity of G(2), G(2) can be regarded as four groups, sequentially denoted as G2(0), G2(1), G2(2) and G2(3).
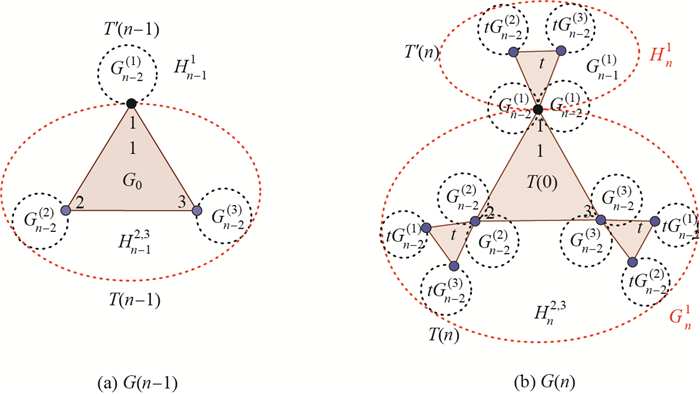
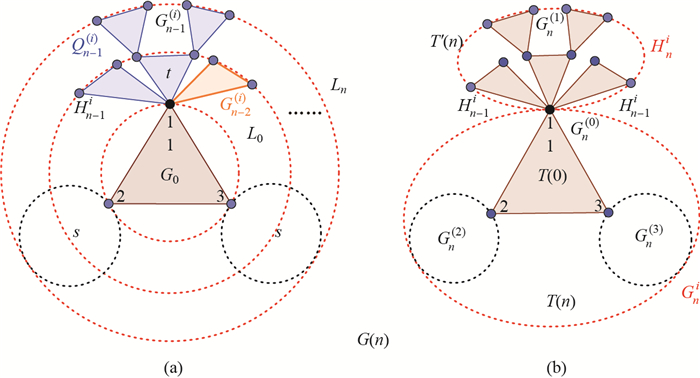
Step n A large network of order k=n+1 is obtained as follows. Firstly, for the convenience of constructing G(n+1), G(n) can be regarded as the merging of Hni and Gni, whose connection nodes are {1, 2, 3}, respectively, as shown in Figure 4(b).
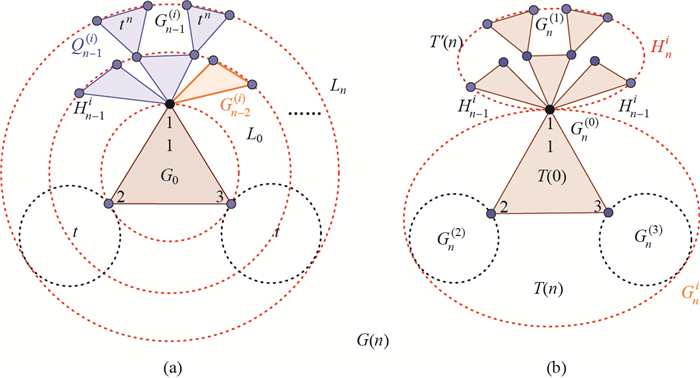
|
图 4 (a) The construction of G(n) as layers; (b) G(n) is regarded as the merging of Hni and Gni Fig.4 (a) The construction of G(n) as layers; (b) G(n) is regarded as the merging of Hni and Gni |
From the self-similarity of G(n), G(n) can be regarded as four groups, sequentially denoted as Gn(0), Gn(1), Gn(2) and Gn(3). One group is Gn(0)=G0-{pi:i=1, 2, 3}; then G(n)-Gn(0) consists of the same three disjoint groups Gn(i), i=1, 2, 3, whose merging node is linked to the corresponding initial merging node pi of G0. Let Gni=(G(n)-Hni)∪ {pi, i=1, 2, 3, then Hni∩ Gni={pi, i=1, 2, 3.
Secondly, let Gn-1(i) be the copy of Gn-1i, i=1, 2, 3, whose weighted edges have been scaled by a factor 0 < t < 1, and let Qn-1(i)=Gn-1(i)∪ Hn-1i, i=1, 2, 3, where Gn-1(i)∩ Hn-1i={pii, i=1, 2, 3, {pii:i=1, 2, 3} is the image of the initially labeled node {pi:i=1, 2, 3}.
Finally, G(n) is obtained by amalgamating three groups Qn-1(i), i=1, 2, 3, and G(n-1) by merging three pairs of pii ∈ Qn-1(i) and pi ∈ G(n-1), i=1, 2, 3, respectively, into a new single node which are then the merging nodes {pi:i=1, 2, 3} ({1, 2, 3} for short) of G(n), as shown in Figure 4(a). Hence, a recursive homogeneous weighted Koch network created by the recursive division method was obtained.
Now, we can easily get some basic quantities, which are needed for this paper. We denote by
| $ \begin{equation} N_k=\sum\limits_{i=0}^{k}L_{\nu}(i)=2\times 4^k+1. \end{equation} $ | (1.1) |
In this section, we will explicitly determine the average homogeneous weighted receiving time (AHWRT)
The mean weighted longest paths (MWLPs) is the expected first arriving weighted time for the walker starting from a source node to a given target node in the layer
From the construction of the homogeneous graph
| $ \begin{equation} F_j(k)=\dfrac{2t(t^k-1)}{t-1}, \forall j\in L_\ell, L_\ell \in H_k^1, \ell=1, \cdots, m, k=1, \cdots, n. \end{equation} $ | (2.1) |
Similarly, in the group
| $ \begin{equation} F_j(k)=\dfrac{2(t^{k+1}-1)}{t-1}, \forall j\in L_\ell, L_\ell \in H_k^{2, 3}, \ell=0, 1, \cdots, m, k=0, 1, \cdots, n. \end{equation} $ | (2.2) |
Here we denote by
| $ \begin{equation} T_{\rm tot}(k)=T^\prime(k)+T(k)=\sum\limits_{j=2}^{N_k}F_j(k). \end{equation} $ | (2.3) |
Now,
| $ \begin{equation} \langle T \rangle_k=\dfrac{T_{\rm tot}(k)}{N_k-1}. \end{equation} $ | (2.4) |
Thus, the problem of determining
For a large network graph
| $ \begin{equation} T^{\prime}(n)=2T^{\prime}(n-1)+tT(n-1). \end{equation} $ | (2.5) |
The group
| $ \begin{equation} T(n)=2tT^{\prime}(n-1)+(t+2)T(n-1)+\dfrac{4}{3}tN_{n-1}+\dfrac{8}{3}N_{n-1}-4. \end{equation} $ | (2.6) |
See Figure 5. If we fix
| $ \begin{equation} K_n=AK_{n-1}+\alpha(n), \end{equation} $ | (2.7) |
|
图 5 (a) The construction of |
where
We can solve Eq (2.7) inductively to get
| $ \begin{equation} K_n=A^nK_{0}+\sum\limits_{i=1}^{n}A^{n-i}\alpha(i). \end{equation} $ | (2.8) |
Now by using singular value decomposition in this work, we seek to find the eigenvalues and the eigenvectors of the matrix
| $ A^{n}= \begin{pmatrix} 2 & t \\ 2t & t+2 \end{pmatrix}^{n} = \begin{pmatrix} \dfrac{1}{3}(2t+2)^{n}+\dfrac{2}{3}(-t+2)^{n} & \dfrac{1}{3}(2t+2)^{n}-\dfrac{1}{3}(-t+2)^{n} \\[3mm] \dfrac{2}{3}(2t+2)^{n}-\dfrac{2}{3}(-t+2)^{n} & \dfrac{2}{3}(2t+2)^{n}+\dfrac{1}{3}(-t+2)^{n} \end{pmatrix}. $ | (2.9) |
By using
| $ A^nK_0= \begin{pmatrix} \dfrac{4}{3}(2t+2)^{n}-\dfrac{4}{3}(-t+2)^{n}\\[3mm] \dfrac{8}{3}(2t+2)^{n}+\dfrac{4}{3}(-t+2)^{n} \end{pmatrix}, $ |
and
| $ \sum\limits_{i=1}^{n}A^{n-i}\alpha(i)= \begin{pmatrix} \dfrac{1}{3}\sum\limits_{i=1}^{n}(2t+2)^{n-i}a_i- \dfrac{1}{3}\sum\limits_{i=1}^{n}(-t+2)^{n-i}a_i\\[3mm] \dfrac{2}{3}\sum\limits_{i=1}^{n}(2t+2)^{n-i}a_i+ \dfrac{1}{3}\sum\limits_{i=1}^{n}(-t+2)^{n-i}a_i \end{pmatrix}. $ |
From Eq (2.8), we get
| $ K_n\!=\! \begin{pmatrix} T^\prime(n) \\ T(n) \end{pmatrix} \!=\!\begin{pmatrix} \dfrac{4}{3}((2t+2)^{n}-(-t+2)^{n})+\dfrac{1}{3}\left(\sum\limits_{i=1}^{n}(2t+2)^{n-i}a_i-\sum\limits_{i=1}^{n}(-t+2)^{n-i}a_i\right) \\[3mm] \dfrac{4}{3}(2(2t+2)^{n}+(-t+2)^{n})+\dfrac{1}{3} \left(2\sum\limits_{i=1}^{n}(2t+2)^{n-i}a_i+\sum\limits_{i=1}^{n}(-t+2)^{n-i}a_i\right) \end{pmatrix}; $ |
then we obtain the formula of
| $ \begin{equation} T^\prime(n)=\dfrac{4}{3}\left((2t+2)^{n}-(-t+2)^{n}\right)+\dfrac{1}{3}\left(\sum\limits_{i=1}^{n}(2t+2)^{n-i}a_i-\sum\limits_{i=1}^{n}(-t+2)^{n-i}a_i\right) \end{equation} $ | (2.10) |
and
| $ \begin{equation} T(n)=\dfrac{4}{3}\left(2(2t+2)^{n}+(-t+2)^{n}\right)+ \dfrac{1}{3}\left(2\sum\limits_{i=1}^{n}(2t+2)^{n-i}a_i+\sum\limits_{i=1}^{n}(-t+2)^{n-i}a_i\right). \end{equation} $ | (2.11) |
By the definition of
\begin{equation*} T_{\rm tot}(n)= 4(2t+2)^{n}+\sum_{i=1}^{n}(2t+2)^{n-i}a_i, \end{equation*}
where
| $ \begin{equation*} T_{\rm tot}(n)= 4(2t+2)^{n}+\dfrac{2}{3}\left(t+2\right)\left(\dfrac{2((2t+2)^n-4^n)}{t-1} \right)+\dfrac{4}{3}\left(t-1\right) \left(\dfrac{(2t+2)^n-1}{2t+1}\right). \end{equation*} $ |
Then for any
| $ \begin{equation} T_{\rm tot}(k)= \dfrac{12t^2(2t+2)^k}{(t-1)(2t+1)}-\dfrac{4^{k+1}(t+2)}{3(t-1)}- \dfrac{4(t-1)}{3(2t+1)}. \end{equation} $ | (2.12) |
Finally, recalling
| $ \begin{align*} \langle T \rangle_k=&\dfrac{6t^2(t+1)^k}{2^k(t-1)(2t+1)}-\dfrac{2(t-1)}{3\times 4^{k}(2t+1)}-\dfrac{2(t+2)}{3(t-1)}. \end{align*} $ | (2.13) |
For a large network, the AHWRT grows as a constant of the network order when the
| $ \begin{equation} \langle T \rangle_k = \dfrac{2(t+2)}{3(1-t)}. \end{equation} $ | (2.14) |
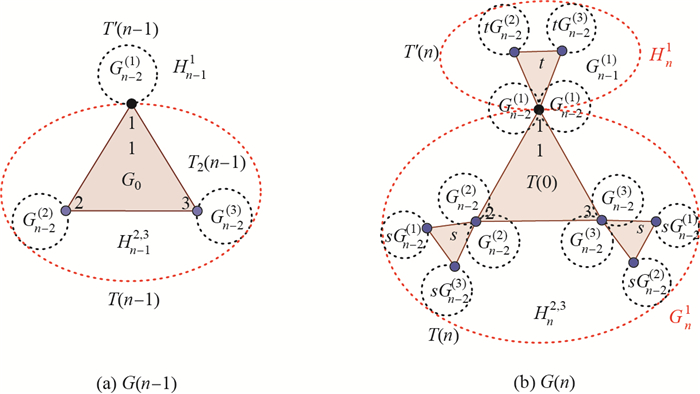
In this section, we will construct recursive non-homogeneous weighted Koch networks. We follow the same topology of Section 1 where the three edges of each equilateral triangle have the same weight. Again, we describe the model using the recursive division method to define recursive non-homogeneous weighted Koch networks. Let us fix two positive real numbers,
Step 1 Given an initial network
Step 2 Let
|
图 6 (a) The construction of |
For the convenience of constructing
Step 3 Let
|
图 7 (a) The construction of |
For the convenience of constructing
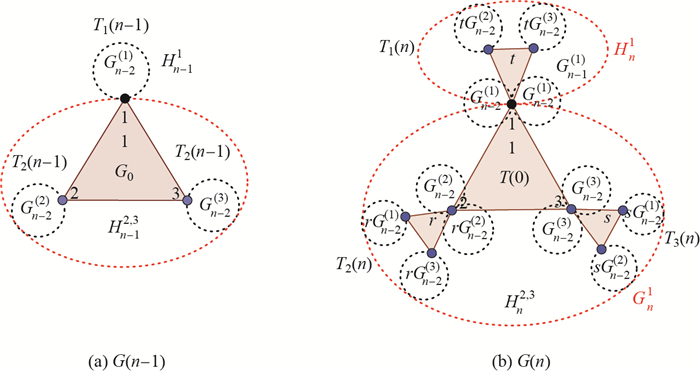
Step n A large network of order
|
图 8 (a) The construction of |
Secondly, let
Finally,
We use the same basic definitions given in Section 2 for all quantities and concepts in this section.
For a large network from the graph, we can obtain the formulas of
The group
| $ \begin{equation*} T^{\prime}(n)=2T^{\prime}(n-1)+tT(n-1). \end{equation*} $ | (4.1) |
The group
| $ \begin{equation*} T(n)=2sT^{\prime}(n-1)+(s+2)T(n-1)+\dfrac{4}{3}sN_{n-1}+\dfrac{8}{3}N_{n-1}-4. \end{equation*} $ | (4.2) |
See Figure 9. If we fix
| $ \begin{equation*} K_n=AK_{n-1}+\alpha(n), \end{equation*} $ | (4.3) |
|
图 9 (a) The construction of |
where
| $ \begin{equation*} K_n=A^nK_{0}+\sum\limits_{i=1}^{n}A^{n-i}\alpha(i). \end{equation*} $ | (4.4) |
Now, by using singular value decomposition in this work, we seek to find the eigenvalues and the eigenvectors of the matrix
| $ A^{n}= \begin{pmatrix} 2&t \\ 2s&s+2 \end{pmatrix}^{n} \\ =\begin{pmatrix} \dfrac{-(s-\alpha)}{2\alpha}\left(\dfrac{s+4+\alpha}{2}\right)^{n}+ \dfrac{(s+\alpha)}{2\alpha}\left(\dfrac{s+4-\alpha}{2}\right)^{n}& \dfrac{t}{\alpha}\left(\dfrac{s+4+\alpha}{2}\right)^{n} -\dfrac{t}{\alpha}\left(\dfrac{s+4-\alpha}{2}\right)^{n} \\[3mm] \dfrac{-(s^2-\alpha^2)}{4t\alpha}\left(\dfrac{s+4+\alpha}{2}\right)^{n}+ \dfrac{(s^2-\alpha^2)}{4t\alpha}\left(\dfrac{s+4-\alpha}{2}\right)^{n}& \dfrac{(s+\alpha)}{2\alpha}\left(\dfrac{s+4+\alpha}{2}\right)^{n}- \dfrac{s-\alpha}{2\alpha}\left(\dfrac{s+4-\alpha}{2}\right)^{n} \end{pmatrix}. $ | (4.5) |
By using
| $ A^nK_0\!=\! \left(\!\! {{\begin{array}{*{20}c}\dfrac{4t}{\alpha} \left(\dfrac{s+4+\alpha}{2}\right)^{n}\!-\! \dfrac{4t}{\alpha}\left(\dfrac{s+4-\alpha}{2}\right)^{n} \\[4mm] \dfrac{2(s+\alpha)}{\alpha}\left(\dfrac{s+4+\alpha}{2}\right)^{n} \!-\!\dfrac{2(s-\alpha)}{\alpha}\left(\dfrac{s+4-\alpha}{2}\right)^{n} \end{array}}}\!\! \right) $ |
and
| $ \sum\limits_{i=1}^{n}A^{n-i}\alpha(i)= \begin{pmatrix} \dfrac{t}{\alpha}\sum\limits_{i=1}^{n}\left(\dfrac{s+4+\alpha}{2}\right) ^{n-i}a_i-\dfrac{t}{\alpha}\sum\limits_{i=1}^{n}\left(\dfrac{s+4-\alpha}{2}\right)^{n-i}a_i \\[3mm] \dfrac{s+\alpha}{2\alpha}\sum\limits_{i=1}^{n}\left(\dfrac{s+4+ \alpha}{2}\right)^{n-i} a_i-\dfrac{(s-\alpha)}{2\alpha}\sum\limits_{i=1}^{n} \left(\dfrac{s+4-\alpha}{2}\right)^{n-i}a_i \end{pmatrix}. $ |
From Eq (4.4) we get
| $ K_n\!=\! \begin{pmatrix} \dfrac{4t}{\alpha}\left(\left(\dfrac{s+4+\alpha}{2}\right)^{n} \!-\!\left(\dfrac{s+4-\alpha}{2}\right)^{n}\right) \!+\!\dfrac{t}{\alpha}\Big(\sum\limits_{i=1}^{n} \left(\dfrac{s+4+\alpha}{2}\right)^{n-i} a_i\!-\!\sum\limits_{i=1}^{n}\left(\dfrac{s+4-\alpha}{2}\right)^{n-i}a_i\Big) \\[3mm] \dfrac{2}{\alpha}\left((s+\alpha)\left(\dfrac{s+4+\alpha}{2}\right)^{n} \!-\!(s-\alpha)\left(\dfrac{s+4-\alpha}{2}\right)^{n}\right) \!+\! \dfrac{1}{2\alpha}\Big((s+\alpha)\sum\limits_{i=1}^{n} \left(\dfrac{s+4+\alpha}{2}\right)^{n-i} a_i\!-\!(s-\alpha)\sum\limits_{i=1}^{n} \left(\dfrac{s+4-\alpha}{2}\right)^{n-i}a_i\Big) \end{pmatrix}. $ |
Then, we obtain the formula of
| $ \begin{align*} T^\prime(n)=&\dfrac{4t}{\alpha}\left(\left(\dfrac{s+4+\alpha}{2}\right)^{n} -\left(\dfrac{s+4-\alpha}{2}\right)^{n}\right) \nonumber\\ &+\dfrac{t}{\alpha}\left(\sum\limits_{i=1}^{n}\left(\dfrac{s+4+\alpha}{2}\right)^{n-i}a_i-\sum\limits_{i=1}^{n}\left(\dfrac{s+4-\alpha}{2}\right)^{n-i}a_i\right) \end{align*} $ | (4.6) |
and
| $ \begin{align*} T(n)=&\dfrac{2}{\alpha}\left((s+\alpha)\left(\dfrac{s+4+\alpha}{2}\right)^{n}-(s-\alpha)\left(\dfrac{s+4-\alpha}{2}\right)^{n}\right) \nonumber\\ &+ \dfrac{1}{2\alpha}\left((s+\alpha)\sum\limits_{i=1}^{n}\left(\dfrac{s+4+\alpha}{2}\right)^{n-i}a_i-(s-\alpha)\sum\limits_{i=1}^{n}\left(\dfrac{s+4-\alpha}{2}\right)^{n-i}a_i\right). \end{align*} $ | (4.7) |
From the definition of
| $ \begin{align*} T_{\rm tot}(n)= &\dfrac{4t+2(s+\alpha)}{\alpha}\left(\dfrac{s+4+\alpha}{2}\right)^{n}-\left(\dfrac{4t+2(s-\alpha)}{\alpha}\right)\left(\dfrac{s+4-\alpha}{2}\right)^{n}\\ &+\dfrac{2t+s+\alpha}{2\alpha}\sum\limits_{i=1}^{n}\left(\dfrac{s+4+\alpha}{2}\right)^{n-i}a_i-\left(\dfrac{2t+s-\alpha}{2\alpha}\right)\sum\limits_{i=1}^{n}\left(\dfrac{s+4-\alpha}{2}\right)^{n-i}a_i, \end{align*} $ |
where
| $ \begin{array}{l} {T_{{\rm{tot}}}}(n) = \frac{1}{{{2^n}}}((4t + 2s + 2\alpha ){(s + 4 + \alpha )^n} - (4t + 2s - 2\alpha ){(s + 4 - \alpha )^n})\;\;\;\;\;\;\;\;\;\;\;\\ \;\;\;\;\;\;\;\;\;\;\;\; - \frac{{(2t + s + \alpha )}}{{3 \times {2^{n - 2}}\alpha }}\left( {\frac{{2(s + 2)({8^n} - {{(s + 4 + \alpha )}^n})}}{{s - 4 + \alpha }} + \frac{{(s - 1)({2^n} - {{(s + 4 + \alpha )}^n})}}{{s + 2 + \alpha }}} \right)\;\;\;\;\;\;\;\;\;\;\;\\ \;\;\;\;\;\;\;\;\;\;\;\; + \frac{{(2t + s - \alpha )}}{{3 \times {2^{n - 2}}\alpha }}\left( {\frac{{2(s + 2)({8^n} - {{(s + 4 - \alpha )}^n})}}{{s - 4 - \alpha }} + \frac{{(s - 1)({2^n} - {{(s + 4 - \alpha )}^n})}}{{s + 2 - \alpha }}} \right). \end{array} $ | (4.8) |
Finally, recalling
| $ \begin{align*} \langle T \rangle_k= &\dfrac{1}{2^{3k+1}\alpha}\left((4t+2s+2\alpha)(s+4+\alpha)^k-(4t+2s-2\alpha)(s+4-\alpha)^k\right) \\[2mm] &-\dfrac{(2t+s+\alpha)}{3\times 2^{3k-1}\alpha}\left(\dfrac{2(s+2)(8^k-(s+4+\alpha)^k)}{s-4+\alpha}+\dfrac{(s-1)(2^k-(s+4+\alpha)^k)}{s+2+\alpha}\right) \\[2mm] &+\dfrac{(2t+s-\alpha)}{3\times 2^{3k-1}\alpha}\left(\dfrac{2(s+2)(8^k-(s+4-\alpha)^k)}{s-4-\alpha}+\dfrac{(s-1)(2^k-(s+4-\alpha)^k)}{s+2-\alpha}\right). \end{align*} $ | (4.9) |
For a large network, the AN-HWRT grows as a constant of the network order when the
| $ \langle T \rangle_k \approx \dfrac{2\times 8^k(s+2)(2t+s-\alpha)}{3\times 2^{-1}\times 2^{3k}\alpha(s-4-\alpha)} -\dfrac{2\times 8^k(s+2)(2t+s+\alpha)}{3\times 2^{-1}\times 2^{3k}\alpha(s-4+\alpha)}. $ |
Hence for
| $ \begin{equation} \langle T \rangle_k=\dfrac{16(t+2)(s+2)}{3(16-8s(t+1))}. \end{equation} $ | (4.10) |
Given the non-homogeneous weighted Koch network is developed in [17], with three scaling factors
Inspired by metabolic networks and airport networks, we introduce recursive non-homogeneous weighted Koch networks in which each edge weight in every triangle is related to the triangle's topology and depends on the scaling factors
We follow the same basic definitions given in Section 2 for all quantities and concepts in this section.
Here, we denote by
| $ \begin{equation} T_{\rm tot}(k)=T_1(k)+T_2(k)+T_3(k)=\sum\limits_{n=1}^{3}T_n(k)=\sum\limits_{j\in G(k)\setminus\{1\}}F_j(k). \end{equation} $ | (6.1) |
Now,
| $ \begin{equation}\label{E:6.2} \langle T \rangle_k=\dfrac{T_{\rm tot}(k)}{N_k-1}. \end{equation} $ | (6.2) |
Thus, the problem of determining
For a large network, from the graph, we can obtain the formulas of
| $ T_1(n)=2T_1(n-1)+tT_2(n-1)+tT_3(n-1). $ | (6.3) |
The group
| $ \begin{equation} T_2(n)=rT_1(n-1)+2T_2(n-1)+rT_3(n-1)+\dfrac{2}{3}rN_{n-1}+\dfrac{4}{3}N_{n-1}-2. \end{equation} $ | (6.4) |
The group
| $ \begin{equation} T_3(n)=sT_1(n-1)+sT_2(n-1)+2T_3(n-1)+\dfrac{2}{3}sN_{n-1}+\dfrac{4}{3}N_{n-1}-2. \end{equation} $ | (6.5) |
See Figure 10.
|
图 10 (a) The construction of |
If we fix
| $ \begin{equation} K_n=AK_{n-1}+\alpha(n), \end{equation} $ | (6.6) |
where
| $ \begin{equation} K_n=A^nK_{0}+\sum\limits_{i=1}^{n}A^{n-i}\alpha(i). \end{equation} $ | (6.7) |
By using singular value decomposition, the matrix of the form
| $ A^{n}= \begin{pmatrix} 2 & t & t \\ r & 2 & r \\ s & s & 2 \end{pmatrix}^{n} =V \begin{pmatrix} \lambda_1^{n} & 0 & 0 \\ 0 & \lambda_2^{n} & 0 \\ 0 & 0 & \lambda_3^{n} \end{pmatrix}V^{-1}. $ | (6.8) |
Researchers can study the last case further and extract the exact formulas
In this work, we have addressed the topic of recursive homogeneous and non-homogeneous weighted Koch networks, where the edges carry the weights of their respective nodes to a given fixed target node. Although such networks appear at first to be substantially more difficult to understand than their unweighted counterparts, we have shown that in many cases recurrence graphs are commonly the best way to understand large and complex networks. The methods presented in this paper, such as the recursive division method, are intended for the study of weighted networks, which are regard as a guide for thinking about such systems. We look forward with interest to learning about other applications of these ideas. Finally, we have discussed the impact of the key parameter
The authors would like to thank Prof. Wenxia Li and Dr. Junjie Miao for the useful discussions.
| [1] |
FRIEZE A, KARONSKI M. Introduction to Random Graphs[M]. Cambridge: Cambridge University Press, 2015.
|
| [2] |
CIEPLAK M, GIACOMETTI A, MARITAN A, et al. Models of fractal river basins[J]. Journal of Statistical Physics, 1998, 91(1/2): 1-15. DOI:10.1023/A:1023069201470 |
| [3] |
ZHAO L, LAI Y C, PARK K, et al. Onset of traffic congestion in complex networks[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2005, 71(2): 026125. DOI:10.1103/PhysRevE.71.026125 |
| [4] |
GARlASCHELLI D, LOFFREDO M I. Fitness-dependent topological properties of the world trade web[J]. Physical Review Letters, 2004, 93(18): 188701. DOI:10.1103/PhysRevLett.93.188701 |
| [5] |
GUIMERA R, AMARAL L A N. Modeling the world-wide airport network[J]. European Physical Journal B, 2004, 38(2): 381-385. DOI:10.1140/epjb/e2004-00131-0 |
| [6] |
MACDONALD P J, ALMAAS E, BARABASI A L. Minimum spanning trees of weighted scale-free networks[J]. Epl, 2005, 72(2): 308-314. DOI:10.1209/epl/i2005-10232-x |
| [7] |
DAI M, SUN Y, SHAO S, et al. Modified box dimension and average weighted receiving time on the weighted fractal networks[J]. Scientific Reports, 2015, 5: 18210. |
| [8] |
WEI D J, LIU Q, ZHANG H X, et al. Box-covering algorithm for fractal dimension of weighted networks[J]. Sci Rep, 2013, 3(6157): 3049. |
| [9] |
CARLETTI T. Stochastic weighted fractal networks[J]. Physics, 2012, 389(10): 2134-2142. |
| [10] |
CARLETTI T, RIGHI S. Weighted fractal networks[J]. Physica A, 2009, 389(10): 2134-2142. |
| [11] |
YUAN Z J, GANG S W, RONG C G. Exact scaling for the mean first-passage time of random walks on a generalized Koch network with a trap[J]. Chinese Physics B, 2012, 21(3): 525-529. |
| [12] |
LI L, SUN W G, WANG G X, et al. Mean first-passage time on a family of small-world treelike networks[J]. International Journal of Modern Physics C, 2014, 25(3): 1350097(10 pages).
|
| [13] |
ZHANG Z, GAO S. Scaling of mean first-passage time as efficiency measure of nodes sending information on scale-free Koch networks[J]. The European Physical Journal B, 2011, 80(2): 209-216. DOI:10.1140/epjb/e2011-10863-1 |
| [14] |
DAI M F, XIE Q, XI L F. Trapping on weighted tetrahedron Koch networks with small-world property[J]. Fractals, 2014, 22(1/2): 1450006(9 pages). https: //www.researchgate.net/publication/263906960_Trapping_on_weighted_tetrahedron_koch_networks_with_small-world_property
|
| [15] |
SUN W. Random walks on generalized Koch networks[J]. Physica Scripta, 2013, 88(4): 045006. DOI:10.1088/0031-8949/88/04/045006 |
| [16] |
DAI M F, YE D D, LI X Y, et al. Average weighted receiving time in recursive weighted Koch networks[J]. Pramana, 2016, 86(6): 1173-1182. DOI:10.1007/s12043-016-1196-8 |
| [17] |
DAI M F, LI X Y, XI L F. Random walks on non-homogenous weighted Koch networks[J]. Chaos:An Interdisciplinary Journal of Nonlinear Science, 2013, 23(3): 033106. DOI:10.1063/1.4810927 |
| [18] |
DONG Y, DAI M, YE D. Non-homogeneous fractal hierarchical weighted networks[J]. Plos One, 2015, 10(4): e0121946. DOI:10.1371/journal.pone.0121946 |




