0 引言

部分子分布函数和碎裂函数是分析高能碰撞过程的两个重要的物理量.部分子分布函数$q(x)$描述的是在一个强子中发现部分子$q$的几率^[1], $x$是部分子带有的动量与强子总动量的比值.对深度非弹性散射(Deep Inelastic Scattering, DIS)过程, Bjorken变量$x=Q^2/2p\cdot q$, $Q^2=-q^2$是散射过程中动量转移的平方.碎裂函数$D(z)$描述的是部分子碎裂为某一强子的几率^[2], $z$是强子的动量与部分子动量的比值.在高能碰撞过程的末态, 胶子或夸克碎裂为强子, 这个过程即为部分子的强子化.在朴素的部分子模型中, 碎裂函数和分布函数是独立于因子化标度的, 即$q$与$D$只是$x$与$z$的函数, 与$Q^2$无关.在QCD(Quantum Chromodynamics, 量子色动力学)改进的部分子模型中, 碎裂函数和分布函数不仅与$x$或$z$有关, 还是标度$Q^2$的函数, 它们的标度演化行为都用DGLAP演化方程^[3]来描述的.如果能确定某一初始标度$Q_{0} ^2$下的碎裂函数和分布函数, 就可以根据DGLAP演化方程得到不同标度下的结果.

本文用$D_{i}^h (z, Q^2)$来标记标度相关的碎裂函数, 它表示胶子或夸克$i$碎裂为某个强子$h$的几率, 其中变量$z=2p\cdot q/Q^2$, $Q^{2}=q^2$是正负电子湮灭过程中质心系能量的平方.可以看出, 在上述定义中, 动量分数$x$和$z$都应满足$0 < x < 1$, $0 < z < 1$.

部分子分布函数和碎裂函数都是非微扰的物理量, 目前不能通过理论方法计算得到, 不同的研究小组都是通过大量拟合实验数据来推断出分布函数和碎裂函数的.现在已经有多个研究小组给出了质子的分布函数, 且被广泛应用, 例如GJR08^[4]、ZRS^[5]、MSTW08^[6]和CTEQ^[7]等.每个小组都拟合出在某一动量标度$Q_0^2 $时部分子的分布函数, 根据DGLAP演化方程演化, 即可得到不同$Q^2$下的分布函数, 从而可与不同的实验进行比较.文献[8]对这几组分布函数做了详细的讨论与比较, 发现不同小组给出的质子的价夸克的分布函数基本是一致的, 海夸克和胶子的分布函数在较大$x$的区域也基本是一致的, 说明目前大家对质子分布函数的认识已比较清晰, 基本得到了正确的质子的分布函数; 然而对于碎裂函数情况就不那么乐观了.为得到质子的碎裂函数, 近年来DSS^[9]、HKNS^[10]和NSM^[11]等研究小组做了大量的努力, 给出了他们的研究结果.但无论是价夸克, 还是海夸克和胶子, 不同小组的差别非常大.本文研究的目的, 就是希望找到碎裂函数与分布函数之间的联系, 通过已有的公认的质子的分布函数来确定部分子碎裂为质子的碎裂函数, 从而减少数值拟合碎裂函数时的不确定性.

本文是这样安排的:第1节对DSS、HKNS和NSM这几个研究小组的质子的碎裂函数进行详细的比较和讨论, 由于这几个研究小组的差别很大, 需要从理论上给予进一步的限制; 第2节分析朴素部分子模型下质子分布函数和碎裂函数的关系, 找到一个简单的联系价夸克分布函数和碎裂函数的关系式, 并建立一组新的碎裂函数的表示形式; 第3节, 通过与实验数据的比较, 分析本文新参数式的合理性, 并对结果进行讨论.

1 几组部分子碎裂函数的分析和比较

部分子碎裂函数是通过正负电子湮灭并碎裂为强子或其他强子产生过程的实验数据进行分析拟合得到的.基本的做法是:先选定一个初始标度$Q_0^2 $, 通常$Q_0^2 \ge {\rm 1 GeV}^{2}$, 在此标度下微扰QCD适用; 然后拟定一个碎裂函数的参数表达形式, 不同研究小组选取的表达式形式不同, 这是带来他们之间差别的一个重要原因; 再选取不同的参数代入表达式, 利用DGLAP演化方程演化到不同标度$Q^{2}>Q_0^{2} $, 与不同标度下的实验结果进行比较, 从而确定参数式的各个参数.由于表达式中参数比较多, 选取不同系列的参数可能会得到类似结果, 也给确定碎裂函数带来困难.另外, 不同标度下的碎裂函数都应满足动量求和规则

$ \begin{equation} \sum\limits_h {\int_0^1 {zD_i^h } } (z, Q^2){\rm d}z=1, \end{equation} $

(1)

即某一部分子最后碎裂成的所有强子的动量总和应该和这个部分子的相等.式(1)中的求和是对所有末态产生的强子求和, 这是对碎裂函数的一个约束条件.但由于实验不可能记录下末态产生的所有强子, 所以实际求和后的结果应该小于1, 这又给确定碎裂函数带来了不确定性.并且, 一个部分子碎裂成的所有不同类型的强子中, 每一种所占的动量比例实验也不确定.这一系列的因素影响了人们对碎裂函数的判断, 它的困难远远大于对部分子分布函数的确定.

目前, 对部分子碎裂为质子的碎裂函数应用比较普遍的是DSS、HKNS和NSM研究小组, 他们都是取$Q_0^{2} =1~{\rm GeV}^2$, 但具体每种部分子的碎裂函数的参数式的形式均不相同. DSS给出的参数式是

$ \begin{align} \left\{\!\! \begin{array}{l} D_{\rm u} =z^{0.041}(1+15(1-z)^{3.44})(0.20714(1-z)^{1.485}-0.193173(1-z)^{1.988}), \\[1mm] D_{\rm d} =z^{0.041}(1+15(1-z)^{3.44})(0.13002(1-z)^{1.485}-0.11805(1-z)^{1.988}), \\[1mm] D_{\overline{\rm u}} ={0.09659}z^{0.041}(1-z)^{1.998}[1+15.0(1-z)^{3.44}], \\[1mm] D_{\overline{\rm d}} ={0.05903}z^{0.041}(1-z)^{1.998}[1+15.0(1-z)^{3.44}], \\[1mm] D_{\rm s} =D_{\overline{\rm s}} =0.{06037}z^{0.041}(1-z)^{1.998}[1+15.0(1-z)^{3.44}], \\[1mm] D_{\rm c} =D_{\overline{\rm c}} =0.33473z^{-0.887}(1-z)^{5.436}, \\[1mm] D_{\rm b} ={3.84107}z^{{0.103}}(1-z)^{{10.0}}, \\[1mm] D_{\rm g} ={2.97933}z^{6.0}(1-z)^{1.{2}}, \end{array} \right. \end{align} $

(2)

其中$D_{\rm u} $和$D_{\rm d} $分别指的是u价夸克和d价夸克碎裂为质子的几率, 其他的指相应的海夸克或胶子碎裂为质子的几率.对c夸克和b夸克分别取$Q_0^{2} =m_{\rm c}^2 $和$Q_0^{2} =m_{\rm b}^2 $.

HKNS给出的参数式形式稍微简洁一些, 为

$ \begin{align} \left\{\!\! \begin{array}{l} D_{\rm u} =2D_{\rm d} ={0.29747}z^{-0.814}(1-z)^{1.628}, \\[1mm] D_{\overline{\rm u}} =D_{\overline{\rm d}} =D_{\rm s} D_{\overline{\rm s}} ={2.32320}z^{0.866}(1-z)^{5.078}, \\[1mm] D_{\rm c} =D_{\overline{\rm c}} ={6.07301}z^{0.683}(1-z)^{7.375}, \\[1mm] D_{\rm b} =D_{\overline{\rm b}} ={2.19402}z^{0.071}(1-z)^{8.802}, \\[1mm] D_{\rm g} ={30.50742}z^{5.0}(1-z)^{2.927}, \end{array} \right. \end{align} $

(3)

且取所有u、d、s海夸克的碎裂函数为相同的分布.

NSM的碎裂函数的参数式形式为

$ \begin{align} \left\{\!\! \begin{array}{l} D_{\rm u} ={0.028}z^{-1.547}(1-z)^{2.710}(1-e^{-0.052z}), \\[1mm] D_{\rm d} =3.382z^{-1.547}(1-z)^{2.710}(1-e^{-0.052z}), \\[1mm] D_{\overline{\rm u}} =7.634z^{-0.053}(1-z)^{5.389}(1-e^{-1.269z}), \\[1mm] D_{\overline{\rm d}} =8.592z^{-0.053}(1-z)^{5.389}(1-e^{-1.269z}), \\[1mm] D_{\rm s} =D_{\overline{\rm s}} =3.110z^{-0.053}(1-z)^{5.389}(1-e^{-1.269z}), \\[1mm] D_{\rm c} =D_{\overline{\rm c}} =4.829z^{{0.733}}(1-z)^{7.046}, \\[1mm] D_{\rm b} =D_{\overline{\rm b}} =10.031z^{0.681}(1-z)^{11.466}, \\[1mm] D_{\rm g} =1.237z^{6.915}(1-z)^{0.482}. \end{array} \right. \end{align} $

(4)

可以看出, 3组参数中, 对c、b夸克和胶子, 研究小组所取的参数形式都相同, 但参数取值完全不一样; 对价夸克和u、d、s海夸克, 研究小组采用了不同的参数式形式.

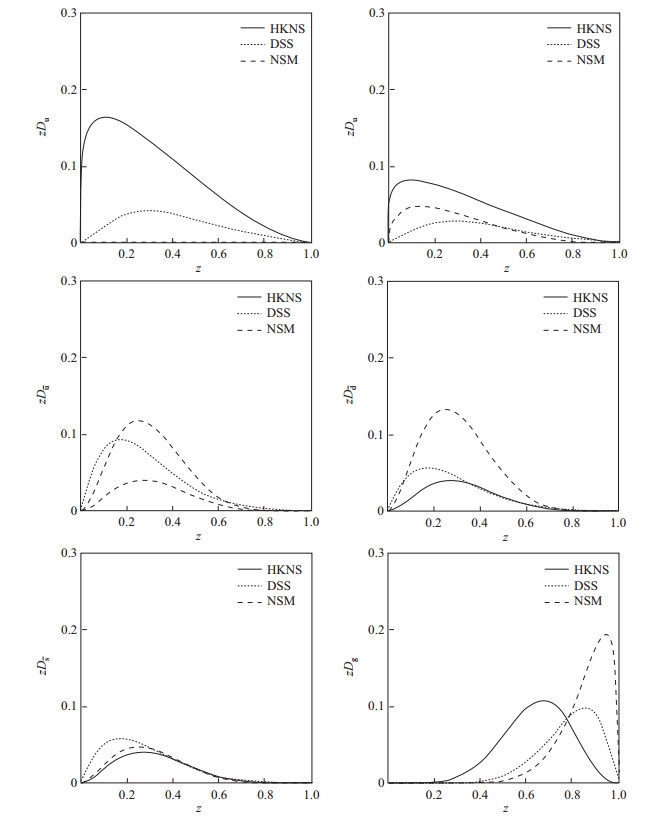
本文比较了DSS、HKNS和NSM在初始标度$Q_0^2 =1~{\rm GeV}^2$时的碎裂函数, 见图 1所示.从图 1可以看出, 除了所有的碎裂函数在$z\to 0$和$z\to 1$时都趋于零外, 所有碎裂函数之间无论是峰值的位置或大小差别都很大, 几乎没有一致性.

研究小组间差别的另一个重要来源, 是对公式(1)的运用.本文计算了$Q^2=1~{\rm GeV}^2$时3个研究小组的不同部分子碎裂为质子的动量比例, 具体见表 1所示.可以看出, 小组间的取值没有相似性.比如, u价夸克, HKNS小组有8.39%(0.083 9)的动量碎裂为质子动量, DSS小组为2.2%(0.022 0), 而NSM小组几乎没有(0.000 2)动量碎裂为质子, 主要的都碎裂为介子去了.在目前人们对质子中部分子分布函数尤其是价夸克分布函数比较确定的情况下, 如果能找到碎裂函数与分布函数间的联系, 就会减少很多参数拟合过程中的不确定性.

2 碎裂函数与分布函数的关系

最早描述部分子分布函数和碎裂函数之间联系的是所谓的DLY(Drell-Levy-Yan)关联^[12-14], 即

$\begin{equation} \dfrac{1}{z}D(z)=q\Big(\dfrac{1}{z}\Big). \end{equation} $

(5)

利用深度非弹性散射和正负电子湮灭过程中强子张量的定义可以对这个联系进行详细的证明. DLY关联指出了碎裂函数可以通过分布函数的解析延拓来得到.但是这个关系中的分布函数和碎裂函数不能同时具有物理意义, 也就是说式(5)把一个过程有物理意义的部分($0 < z < 1)$和另一个过程没有物理意义的部分(${1/}z>1)$联系在一起了, 所以这个公式仅仅是在解析推导上有意义.随后, Gribov-Lipatov关联(G-L关联)^[15]以$D(z)\propto q(x)$的形式将$D(z)$和$q(x)$联系起来, 这个联系中$x=z$, 当$z\to 1$时它的修正的形式是

$ \begin{equation} D_q (z)=zq(z). \end{equation} $

(6)

后来, 马伯强和他的合作者提出了一个新的关系式^[16]

$ \begin{equation} \frac{D(z)}{z}\cong zq\Big(2-\dfrac{1}{z}\Big). \end{equation} $

(7)

这个关系是在DLY的基础上得到的, 当$z\ge 0.5$时, 分布函数和碎裂函数都有物理意义; 然而, 这个联系只能只用于大$z$的范围, 不能在通常情况下使用, 并且在$z\to 1$时$2-\frac{1}{z}\to z$, 这个联系与G-L关联是相似的.最重要的是, 当利用这些联系将分布函数转化为碎裂函数时, 可以发现这样得到的碎裂函数不能很好地描述实验数据.

本文在拟合数据的过程中, 发现关系式

$ \begin{equation} D(x)=\frac{1}{6}q(x) \end{equation} $

(8)

可以很好地描述质子的价夸克分布函数和价夸克碎裂为质子的碎裂函数之间的联系, 尤其是在大$x$区域.现在对式(8)进行一个简单的推导.从以上提到的$x$和$z$的定义知道, 它们有共同的取值范围和相似的物理意义, $0 < x < 1$, $0 < z < 1$, 所以在下面的讨论中分布函数和碎裂函数都用$x$来标记变量.深度非弹性散射截面的计算是由两个结构函数$F_1 (x)$和$F_2 (x)$组成, 在领头阶近似下Callan-Gross关系^[17]把这两个结构函数联系起来, 即

$ \begin{equation} F_2 (x)=2xF_1 (x). \end{equation} $

(9)

同样, 正负电子湮灭截面的计算是由$ \overline{F} _1 (x)$和$ \overline{F} _2 (x)$组成, Gribov-Lipatov关系^[18-20]

$ \begin{align} x \overline{F} _1 (x)=F_1 (x) \end{align} $

(10)

和

$ \begin{align} x^3 \overline{F} _2 (x)=-F_2 (x) \end{align} $

(11)

把深度非弹性散射和正负电子湮灭过程的结构函数给联系起来.将式(10)和式(11)代入到式(9), 可以得到

$ \begin{equation} \overline{F} _1 (x)=-\frac{x}{2} \overline{F} _2 (x), \end{equation} $

(12)

领头阶的正负电子湮灭截面^[21]为

$ \begin{equation} \frac{{\rm d}\sigma ^h}{{\rm d}x}=\frac{2\alpha ^2\pi x}{q^2}\Big( \overline{F} _1^h (x, q^2)+\frac{x}{6} \overline{F} _2^h (x, q^2)\Big)=-\frac{2\alpha ^2\pi x^2}{3q^2} \overline{F} _2^h (x, q^2). \end{equation} $

(13)

又由于$e^+e^-\to hX$的总截面为

$ \begin{equation} \sigma _{\rm tot} =\frac{4\pi \alpha ^2}{q^2}\sum\limits_q {e_q^2 =\frac{4\pi \alpha ^2}{3q^2}} R, \end{equation} $

(14)

根据$R$的定义^[21], 可以得到

$ \begin{equation} \frac{1}{\sigma _{\rm tot} }\cdot\frac{{\rm d}\sigma }{{\rm d}x}=-\frac{x^2}{2R} \overline{F} _2^h (x). \end{equation} $

(15)

微分截面^[22]用碎裂函数又可以表示为

$ \begin{equation} \frac{1}{\sigma _{\rm tot} }\cdot\frac{{\rm d}\sigma }{{\rm d}x}=\frac{1}{R}\times 3\times \sum\limits_a {e_a^2 } (D_a^h (x)+D_{\overline{a}}^h (x)), \end{equation} $

(16)

其中$a$指的是夸克的味道, 因子"3"来源于颜色求和.比较式(15)和式(16)有

$ \begin{equation} \overline{F} _2^h (x)=-\frac{6}{x^2}\times \sum\limits_a {e_a^2 } (D_a^h (x)+D_{\overline{a}}^h (x)). \end{equation} $

(17)

又因为领头阶的结构函数$F_2 (x)$为

$ \begin{equation} F_2 (x)=\sum\limits_a {e_a^2 } (xq_a (x)+xq_{\overline{a}} (x)), \end{equation} $

(18)

由式(11)可知

$\begin{equation} {-6}\times \sum\limits_a {e_a^2 (xD_a^h (x)+xD_{\overline{a}}^h (x))} =-\sum\limits_a {e_a^2 } (xq_a (x)+xq_{\overline{a}} (x)), \end{equation} $

(19)

于是可以得到式(8).推导完毕.

虽然以上分析都是在领头阶下成立, 没有考虑QCD修正.但不妨碍假定在$Q^2=1~{\rm GeV}^2$的标度下, 价夸克的碎裂函数和分布函数间存在上述关系, 以它为基础建立碎裂函数的分布形式.本文利用ZRS^[5]的$Q^2=1~{\rm GeV}^2$的价夸克分布函数作为基础, 根据式(8)得到相应的碎裂函数, 并把它们参数化.海夸克的碎裂函数本文采用类似DSS的参数式, 表达式如下.

$ \begin{align} \left\{\!\! \begin{array}{l} xD_{\rm u}^v =0214x^{0.35}(1-x)^{3.04}(1-2.374x^{0.5}+8.992x), \\ xD_{\rm d}^v =0.815x^{0.67}(1-x)^{5.12}(1-4.365x^{0.5}+7.473x), \\ xD_{\rm s} =0.121x^{0.84}(1-x)^{2.0}(1+15.0(1-x)^{3.44}+8.992x), \\ xD_{\overline{\rm u}} =0.097x^{0.84}(1-x)^{2.0}(1+15.0(1-x)^{3.44}+8.992x), \\ xD_{\overline{\rm d}} =0.059x^{0.84}(1-x)^{2.0}(1+15.0(1-x)^{3.44}+8.992x), \\ xD_{\rm g} =2.979x^{7.0}(1-x)^{1.2}. \end{array} \right. \end{align} $

(20)

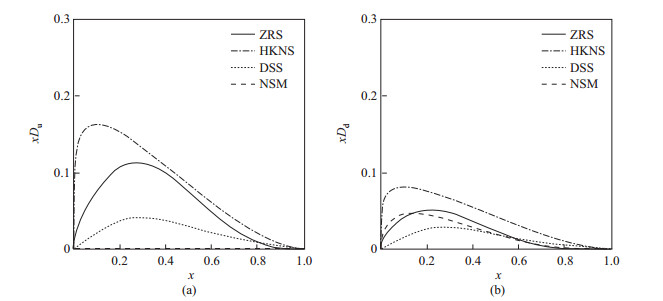
如图 2所示, 图中实线是公式(20)中的$xD_{\rm u}^v $和$xD_{\rm d}^v $, 其他3组分别是DSS、HKNS、NSM相应的碎裂函数, 可以看出, 本文的函数分布与任何一个都不一样, 但在它们的范围之内.

3 结果与讨论

正负电子湮灭$e^++e^-\to p+X$过程领头阶的微分散射截面如公式(16)所示, 其中系数$R=\sum\limits_a {3e_a^2 } $.以式(19)作为输入函数, 代入DGLAP演化方程进行演化计算, 得到不同动量标度下的碎裂函数, 再代入公式(16)就可以和实验结果进行比较.

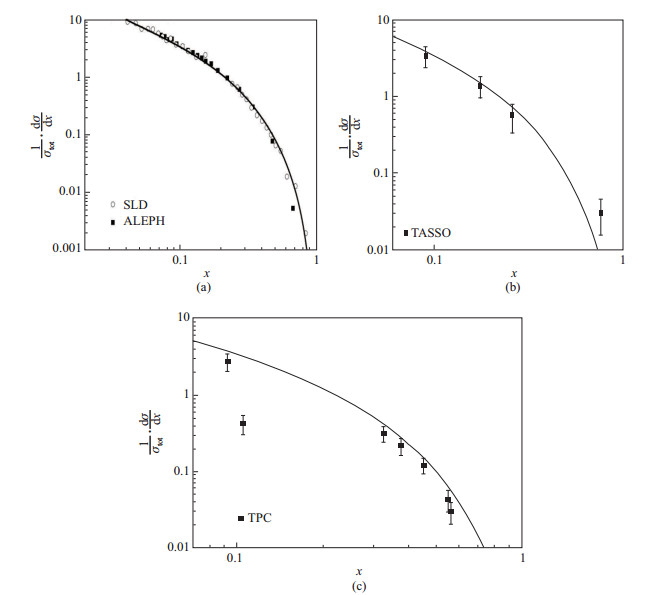
图 3是正负电子湮灭的微分散射截面实验数据和本文的计算结果.图(a)是正负电子湮灭质心系能量$\sqrt s =91.2~{\rm GeV}$时的散射截面实验数据^[23-24], 图(b)是TASSO^[25]在$Q=34$ GeV的实验数据, 图(c)是TPC^[26-27]在$Q=29$ GeV的实验结果.可以看到, 对图(a)和(b), 本文的数据和实验结果符合非常好; 而从图(c)来看, 本文的数据稍微偏大些, 在以后的工作中, 我们会考虑更多的实验数据, 争取能得到更精确的胶子和海夸克的碎裂函数的分布.

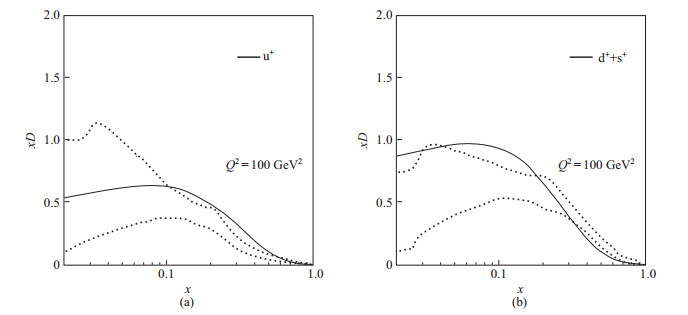
最近, 文献[28]研究小组给出了他们的最新的碎裂函数的结果, 有一个非常宽的取值范围. 图 4是本文的结果与其的比较, 图中的两条虚线指的是他们结果的上下限, 实线是本文结果.其中u$^+$指的是对所有的u夸克求和, d$^+$+s$^+$指的是对所有的d、s夸克求和, 并且这些求和中包括了质子和反质子.从图 4可以看出, 本文的结果u$^+$在$x>0.1$的部分略超出文献[28]的范围, 而d$^+$+s$^+$在$x<0.2$的部分略超出文献[28]的范围.

在以上的讨论中, 是把价夸克的碎裂函数和分布函数联系起来, 利用比较成熟的价夸克的分布函数来得到相应的碎裂函数, 从而省去了拟合价夸克碎裂函数的大量不确定因素.然而关系式(8)对海夸克和胶子是不适用的, 原因是Callan-Gross关系仅适用领头阶自由夸克的散射.本文比较了现有的海夸克和胶子的分布函数和碎裂函数的关系, 发现它们之间的联系与式(8)相差很远, 所以, 要得到比较可信的胶子和海夸克碎裂函数还需要继续探索.事实上, 关系式(8)也不能用来解释介子中价夸克的分布函数和碎裂函数之间的联系, 因为Callan-Gross关系是自旋为1/2的场的结论而不是自旋为0的场.