2. 国防科技大学 气象海洋学院, 南京 211101
2. College of Meteorology and Oceanography, National University of Defense Technology, Nanjing 211101, China
近岸浅水区水深测量具有重要意义.人类开发利用海洋的大量活动集中在近岸浅水区, 海岸防护、港口建设、航道开辟与维护、围海造田、铺设海底电缆与输油管道、海洋能源开发等都需要详细的水深资料.河流来沙、海岸侵蚀为近岸浅水区提供了丰富的沙源, 水动力条件又有利于泥沙运动, 泥沙运动使其水深处于频繁变动中, 泥沙冲淤和其他海洋研究需要频繁观测更新的水深资料.一些岛屿是部分国家、地区之间领土争议的焦点, 这些岛屿延伸的近岸浅水区是政治和军事关注的重点区域, 其水深测量是国防建设的重点内容.
常规水深观测一般采用船载钢丝绳测深或声纳测深方法.其中, 船载声纳测深的测量精度高, 是目前最可靠和有效的测量方法[1].但是这两种方法需要大量的人力和物力, 而且不适用于船只不能进入的浅滩和有争议的海域.近年来遥感测深方法得到快速发展, 航空双介质摄影测深[2]、机载激光测深[3]、可见光遥感测深[4-6]、海表面短波的SAR图像反演海底地形[7-9]等方法在近岸浅水区得到很多应用, 它们具有快速、大面积、准同步、高分辨率获取水深能力.但是这些遥感测深方法也存在一些局限性[1].例如, 航空双介质摄影测深、机载激光测深和可见光遥感测深都受到水体混浊度影响, 我国很多近岸浅水区属于二类水体, 影响测深效果.可见光遥感测深在底质类型复杂海区效果也不好[10].海表面短波的SAR图象反演海底地形受到气象条件、潮流流速、常规水深和流场观测资料限制[9].对于有争议的海域, 航空双介质摄影测深和机载激光测深受航高限制, 不能实现水深测量.
利用遥感资料反演海浪, 再利用海浪信息反演近岸水深, 是近年来发展的另外一种遥感水深测量方法.近岸浅水区海浪接近于浅水重力波, 海浪要素对水深变化非常敏感[11].水深变浅, 波速、波长会变小, 水深变化还会造成波向折射及波高变化.反过来, 通过遥感海浪要素的空间分布反演水深, 可以实现近岸浅水区水深测量[12-13]. Bell等[14]使用X波段的雷达影像获取波速和波向的空间分布, 基于线性波动的频散关系反演水深. Leu等[15]选取两幅时间不同的SPOT-3可见光卫星图像, 通过快速傅里叶变换(FFT)提取波长和波向, 由波动频散关系式反演台湾地区西海岸台中港附近海域的水深, 在水深小于12 m的浅水区测深效果较好.陈台颖[16]、柯绅彦[17]直接对FORMOSAT-2卫星影像进行图像分析, 获得波长, 并利用波长反演水深. Li[18]等仅使用单幅高分辨率的可见光遥感影像, 通过FFT方法反演三亚湾海浪波长和水深, 均方根误差和相对误差分别为1.07m和16.2%. Poupardin[19]利用两幅SPOT-5全色和多光谱影像, 基于小波变换方法反演波长和水深, 也取得了较好的效果.利用遥感波浪反演水深的方法, 具有受海水浊度、底质特征影响小的优点, 对常规水深观测资料的依赖也很少.但是目前对该方法的研究和推广应用远落后于航空双介质摄影测深、机载激光测深、可见光遥感测深、SAR图像反演海底地形方法.
一般而言, 高分辨率遥感资料可以反演更精确的海洋信息, 但是价格昂贵.基于FFT方法反演海浪波长和水深, 是一种比较容易实现的方法, 也得到了比较好的检验.在该方法中, 遥感资料分辨率对海浪波长和水深的反演结果有什么影响?这是一个值得研究的问题, 目前缺乏深入分析.为了更清晰直观地认识遥感反演水深方法的某些性能, 有不少研究工作没有直接采用遥感资料, 而是开展其他替代性资料的仿真分析[20].本文利用理想波面数据代替遥感资料, 仿真分析资料分辨率对FFT方法反演波长的影响, 还探讨了该方法涉及的子图长度选取问题; 利用理想地形上的数值模拟波面数据代替遥感资料, 仿真分析资料分辨率和子图长度对FFT方法反演波长和水深的影响.
1 基于FFT方法反演海浪波长及水深的原理随空间变化的资料序列可以看成由若干个不同波长的波动合成, 离散傅立叶变换方法是寻找其中最显著波动的一种常见方法.对于包含海浪波面信息的遥感资料, 也可以采用离散傅里叶变换方法反演波数能量谱, 确定其中能量最强的主波波数及波长[15].离散傅里叶变换方法将遥感影像划分为若干幅N
| $ \begin{align} F(k_x, k_y)=\dfrac{1}{N^2}\sum\limits^{N-1}_{m_2=0} & \left[\sum\limits^{N-1}_{m_1=0}X(m_1, m_2) \cdot {\rm e}^{-{\rm i}n_{x}k_0m_1\Delta X}\right]\cdot {\rm e}^{-{\rm i}n_{y}k_0m_1\Delta X}, \end{align} $ | (1) |
| $ \begin{align} \Psi(k_x, k_y)=|F(k_x, k_y)|^2. \end{align} $ | (2) |
其中,
| $ \begin{align} \Big[-\dfrac{N}{2}k_0, \dfrac{N}{2}k_0\Big]. \end{align} $ | (3) |
从波数能量谱中提取谱峰最高值对应的波数
| $ \begin{align} &{L}=\dfrac{2\pi}{\sqrt{(k_{px})^2+(k_{py})^2}}, \end{align} $ | (4) |
| $ \begin{align} &\theta_p={\rm arctan}\Big(\dfrac{k_{py}}{k_{px}}\Big). \end{align} $ | (5) |
当波浪由深水区传播至近岸浅水区时, 波长随着水深变浅而减小.近岸浅水区水深和波长的关系近似用线性波动频散关系式描述:
| $ \begin{align} {h}=\dfrac{L}{2\pi}{\rm tanh}^{-1}\Big(\dfrac{2\pi L}{gT^2}\Big). \end{align} $ | (6) |
其中,
| $ \begin{align} {T}=\sqrt{\dfrac{2\pi L}{{g}}}. \end{align} $ | (7) |
根据遥感影像反演的深水区波长和(7)式可以计算波周期.
2 利用理想波面资料反演波长的仿真分析海水中理想规则波动的波剖面方程可用正弦或余弦曲线表示[11].利用余弦形式的波动构造理想波面:
| $ \begin{align} \eta=A\cos\dfrac{2\pi x}{{L}}. \end{align} $ | (8) |
其中
| $ \begin{align} \eta=A\cos\Big(\dfrac{2\pi j\Delta x}{{L}}\Big). \end{align} $ | (9) |
其中
| 表 1 波长为70m的理想波面资料反演的波长 Tab.1 Wavelengths from inversions by elevation data at a wavelength of 70 m |
| 表 2 波长为90m的理想波面资料反演的波长 Tab.2 Wavelengths from inversions by elevation data at a wavelength of 90 m |
| 表 3 波长为110m的理想波面资料反演的波长 Tab.3 Wavelengths from inversions by elevation data at a wavelength of 110 m |
进一步分析表 1中0.25~32m与64m分辨率资料对波长反演结果产生不同影响的原因. FFT方法按(3)式给定的波数序列计算谱能量.
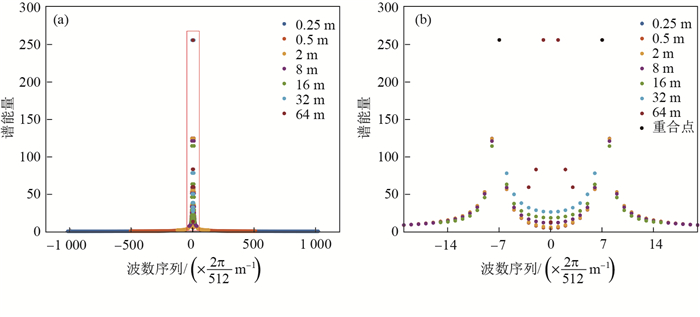
图 1给出了波面资料波长为70m、子图长度为512m的情况下, 不同分辨率资料计算的波数能量谱.每种分辨率资料计算的波数能量谱都是关于正、负波数对称的, 本文仅讨论波数为正的情况.资料分辨率为0.25m时波数能量谱包含的波数序列为
|
注:波面资料的波长为70m, 子图为512m; (b)为(a)中红色框部分的放大显示图; 谱能量为归一化到0~255的值; (b)中重合点为0.25m, 0.5m, 2m, 8m, 16m和32m的谱能量峰值点 图 1 不同分辨率的波面资料计算的波数能量谱 Fig.1 Wavenumber spectrum calculated by elevation data using different resolutions |
本文还利用余弦形式的波动构造两种波动组合的理想波面资料:
| $ \begin{align} \eta=A_1\cos\dfrac{2\pi x}{L_1}+A_2\cos\dfrac{2\pi x}{L_2}. \end{align} $ | (10) |
| 表 4 组合波动(振幅之比1.2)的理想波面资料反演的波长 Tab.4 Wavelengths from inversions by elevation data including two fluctuations with an amplitude ratio of 1.2 |
| 表 5 组合波动(振幅之比1.6)的理想波面资料反演的波长 Tab.5 Wavelengths from inversions by elevation data including two fluctuations with an amplitude ratio of 1.6 |
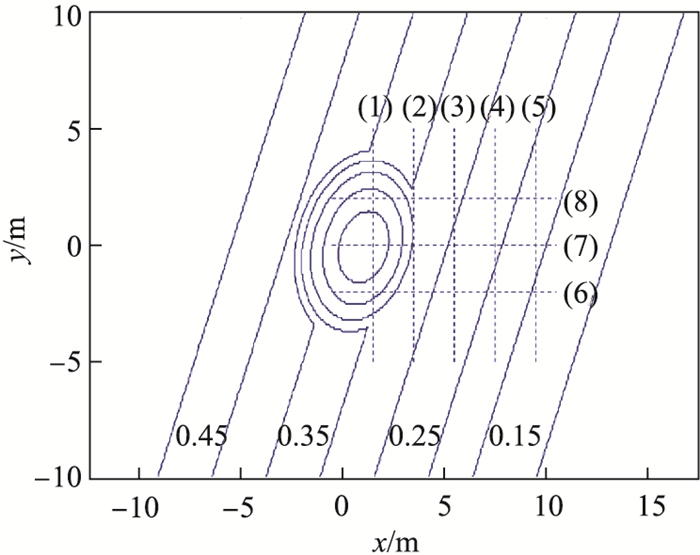
近岸海浪在地形作用下波长和振幅都会发生变化.本文采用FUNWAVE模式提供近岸地形上的波面仿真资料, 反演波长和水深. FUNWAVE模式由美国特拉华大学研制, 采用了Boussiniesq方程, 能够较好地模拟近岸海浪的浅化、折射、绕射、破碎等变化过程[22].本文采用它的最新TVD版本[23].首先利用Berkhoff[24]的波浪水槽实验数据, 对FUNWAVE模式进行检验.如图 2所示, 设置坡度为0.02的斜坡, 斜坡前水深为0.45m, 斜坡上叠加沙坝.入射波的波向与斜坡呈20
|
注:图中(1)-(8)为波高观测断面, 0.15、0.25、0.35、0.45表示等深线的水深值(单位为m); 横纵坐标轴分别表示x, y方向上的位置 图 2 Berkhoff的波浪水槽实验设置[24] Fig.2 The layout of the wave flume experiment made by Berkhoff[24] |
|
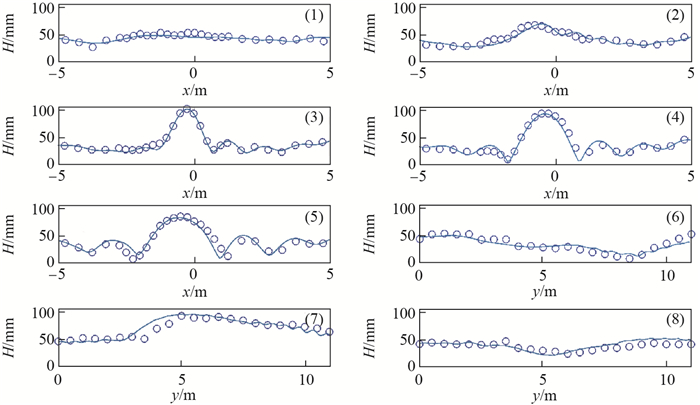
注:实线为计算值, 圆圈为水槽实验值 图 3 FUNWAVE对波浪水槽实验中(1)-(8)断面波高的模拟检验 Fig.3 Waveheight test to FUNWAVE simulating the wave flume experiment at sections of (1)-(8) |
本文选取江苏中部平缓淤泥质海岸作为参考设置数值模拟方案, 该区域水深介于0
|
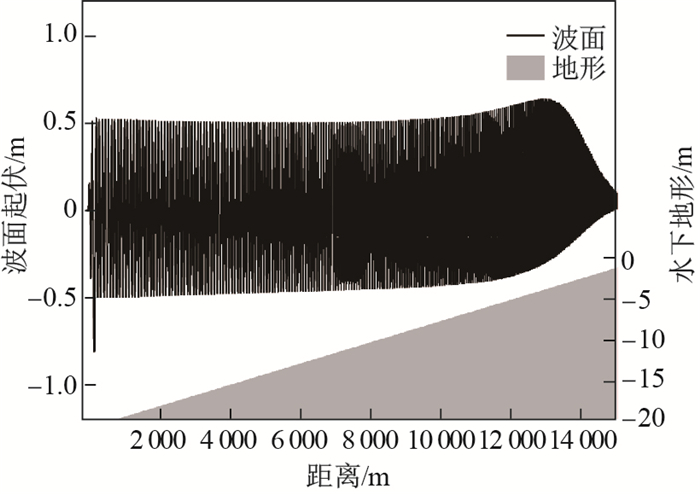
图 4 在斜坡地形上FUNWAVE模式模拟的波面 Fig.4 Simulated elevation data on a slope by FUNWAVE |
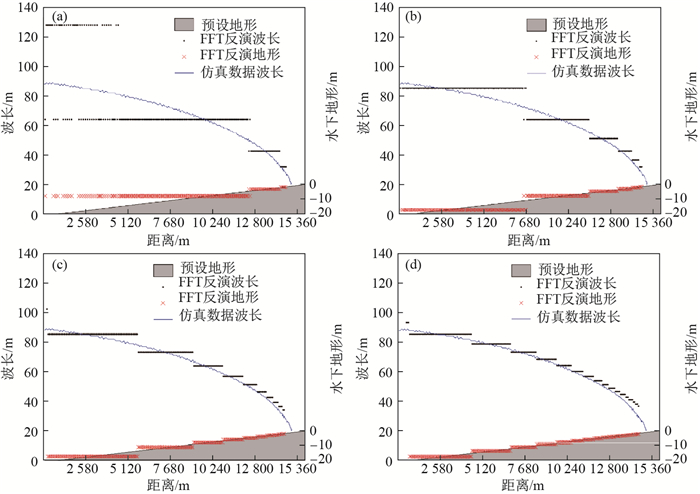
利用图 4的1m分辨率波面数据, 由FFT方法反演波长, 再基于波长反演水深.在划分子图时, 子图中心点的间隔为64 m, 两个相邻子图覆盖的区域有部分重叠. 图 5给出FFT方法反演的波长和地形(即水深). 图 5还给出了数值模拟方案设置的地形(简称预设地形)以及由数值模拟仿真波面数据直接分析得到的波长(简称仿真数据波长)用于对比. 图 5(a)选用的子图长度为128 m, FFT方法反演波长与仿真数据波长差别很大, 反演的水下地形与预设地形也有很大差别. 图 5(b)-(d)选用的子图长度分别为256、512、1 024 m, FFT方法反演波长与仿真数据波长差别比较小, 反演的水下地形与预设地形也比较接近. 表 6给出了反演地形(水深)对于预设地形的误差统计.子图长度为128和256m时, 水深反演误差比较大; 子图长度为512和1 024 m时, 水深反演误差比较小.在0-3 m水深段, 子图长度512 m的水深反演误差小于子图 1024 m的水深反演误差; 在3-20 m水深段, 子图长度512 m的水深反演误差大于子图 1024 m的水深反演误差.总体而言, 在3-12 m水深段, 子图长度512和1 024 m的水深反演平均相对误差最小.
|
注: (a)-(d)的子图长度分别为128、256、512、1 024m 图 5 在斜坡地形上基于数值模拟仿真数据反演的波长和地形 Fig.5 Wavelengths and topographies from inversions using the simulated elevation data on a slope |
| 表 6 在斜坡地形上利用数值模拟仿真数据反演水深的误差统计 Tab.6 Errors of water depths from inversions using the simulated elevation data on a slope |
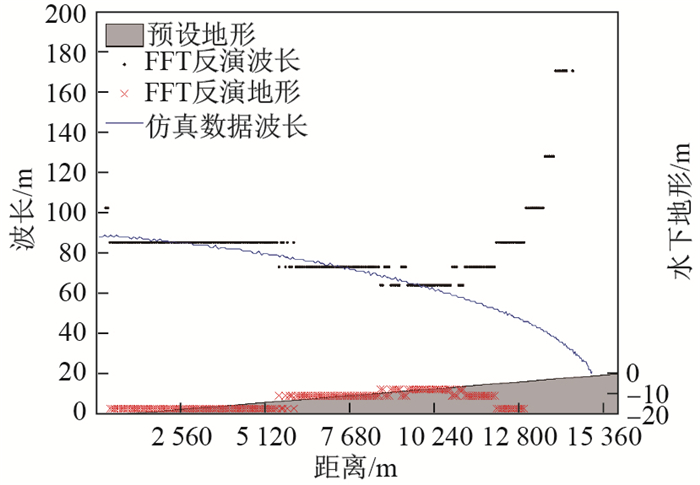
本文还从图 4的数据中跳点获得分辨率分别为2、4、8、16、32 m的数值模拟仿真数据, 子图长度取为512 m, 利用FFT方法反演波长和水深(地形). 2、4、8、16 m分辨率资料反演波长和地形与图 5(c)结果一致, 在0-20 m水深段反演地形与预设地形的平均相对误差为9.60%.但是, 32m分辨率资料反演波长和地形(见图 6)与图 5(c)有很大差异, 反演地形与预设地形的平均相对误差为37.69%.
|
图 6 在斜坡地形上32m分辨率资料反演的波长和地形 Fig.6 Wavelengths and topographies from inversions using the simulated elevation data with 32 m resolution on a slope |
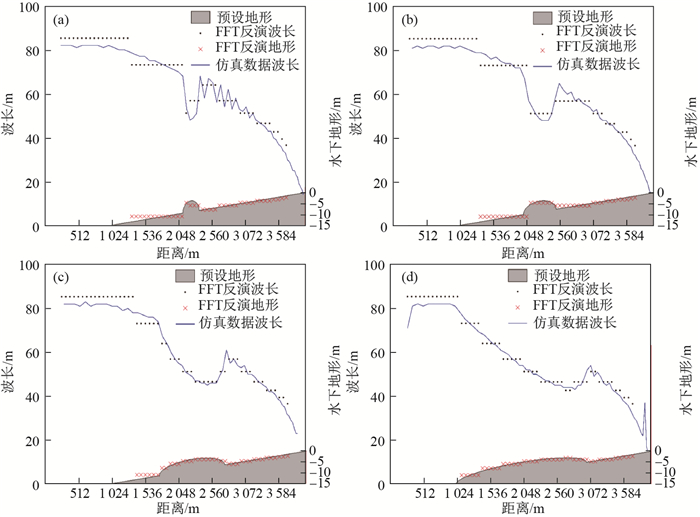
本文还在斜坡上设置不同尺寸的沙坝, 采用FUNWAVE模式模拟波面数据.斜坡坡度为0.005;沙坝为半椭圆形, 其长半轴沿斜坡方向分别设为125、250、500和1 000 m, 短半轴为沙坝高度, 其值为5 m, 垂直于斜坡方向地形无变化; 斜坡前平底水深为15 m; 计算网格分辨率为1 m; 入射波周期为8 s, 入射波高为1 m.模式运行稳定后取某个时刻的1 m分辨率波面数据, 采用FFT方法反演波长和水深. 表 7给出了沙坝段反演水深(地形)相对于预设地形的平均误差.沙坝尺寸(即椭圆长半轴)为125 m和250 m时, 子图长度256 m反演水深的误差小于其他子图长度反演水深的误差; 沙坝尺寸为500 m和1 000 m时, 子图长度512 m反演水深的误差小于其他子图长度反演水深的误差. 图 7出了在不同尺寸沙坝上子图长度512 m演的波长和地形. 图 7(a)和(b)的沙坝尺寸分别为125 m和250 m, 反演地形不能较好地拟合预设地形的变化. 图 7(c)和(d)的沙坝尺寸分别为500 m和1 000 m, 反演地形较好地拟合预设地形的变化.从图 7可以看出, 沙坝上波长基本上在50~70m之间, 子图长度128 m仅相当于2倍波长左右, 因此, 表 7中在所有尺寸沙坝地形上, 子图长度128 m反演水深的误差都很大.子图长度256 m相当于4倍波长左右, 子图长度512 m相当于8倍波长左右, 在沙坝尺寸125m和250 m的地形上子图长度256 m子图长度512 m反演水深误差小, 而在沙坝尺寸500 m和1 000 m的地形上这两种子图反演水深的对比效果结果相反.子图长度512 m尽管包包含的波长多, 但是对于沙坝尺寸125 m和250 m的地形而言, 它远大于沙坝地形变化尺度, 在每个子图计算的波数能量谱中包含大量的非沙坝地形信息, 因而不能较好地反演沙坝地形.子图长度1 024 m包含的波长更多, 其尺度也与沙坝尺寸1 000 m相当, 但是它对该沙坝的水深反演效果并没有优于子图长度512 m.综合表 7和图 7来看, 子图长度太大或太小, 反演水深的误差都比较大, 在子图长度为波长的4~8、并且小于或等于地形变化尺度的情况下, 反演水深的效果好.
| 表 7 在沙坝地形上利用数值模拟仿真数据反演水深的误差统计 Tab.7 Errors of water depths from inversions using the simulated elevation data on bars |
|
注: (a)-(d)的沙坝地形呈椭圆形, 其长半轴分别为125、250、500和1 000 m 图 7 在沙坝地形上子图长度512 m反演的波长和地形 Fig.7 Wavelengths and topographies from inversions using the simulated elevation data on bars |
利用海浪波峰和波谷位置的遥感信息差异, 可以基于快速傅里叶变换(FFT)方法反演波长, 还可以利用波长反演近岸水深.本文采用余弦函数的理想波面数据和FUNWAVE模式的数值模拟波面数据代替遥感资料进行仿真研究, 讨论资料分辨率和子图尺度对海浪波长及水深反演的影响.理想波面数据的仿真应用研究表明: ①当波长不存在空间变化时, 子图越大, 波长反演误差越小, 子图长度为4倍波长以上时波长反演效果比较好, 子图长度小于2倍波长时波长反演效果不好; ②在子图长度满足要求的情况下, 低分辨率资料反演波长的效果差, 但是如果资料分辨率达到一定要求(每个波长内资料点不少2个), 再提高资料分辨率对波长的反演结果没有影响; ③主波和次要波的振幅不能太接近, 两者之比为1.5倍以上, 才能较好地反演主波波长.在斜坡和沙坝地形上的数值模拟波面数据仿真应用研究表明:在非均匀变化的地形上, 要求子图长度适中, 即子图长度为4~8倍波长、并且小于或等于地形变化尺度, 子图太大和太小都不能较好地反演水深(地形).这些仿真研究结论可以为实际遥感资料反演海浪波长和水深提供参考.本文利用斜坡上的数值模拟波面数据仿真应用, 初步比较了在不同水深段的水深反演误差.但是尽管FUNWAVE是国际上近岸海浪波面数值模拟中最有代表性的模式之一, 它对较长周期或较深水域的海浪波面数值模拟能力仍需进一步提高, 本文还不能通过这种数值模拟仿真研究进行更充分、更全面的讨论.后续研究中将在实际海域通过遥感资料反演海浪波长和水深, 可以更好地分析遥感海浪波长反演水深的适用水深范围.
| [1] |
申家双, 潘时祥. 沿岸水深测量技术方法的探讨[J]. 海洋测绘, 2002, 22(6): 60-65. DOI:10.3969/j.issn.1671-3044.2002.06.016 |
| [2] |
周高伟, 李英成, 任延旭, 等. 低空无人机双介质水下礁盘深度测量试验与分析[J]. 测绘学报, 2015, 44(5): 548-554. |
| [3] |
刘焱雄, 郭锴, 何秀凤, 等. 机载激光测深技术及其研究进展[J]. 武汉大学学报(信息科学版), 2017, 42(9): 1185-1194. |
| [4] |
张鹰, 张东, 王艳姣, 等. 含沙水体水深遥感方法的研究[J]. 海洋学报, 2008, 30(1): 51-58. DOI:10.3321/j.issn:0253-4193.2008.01.007 |
| [5] |
沈婕, 苏昆, 张鹰, 等. 基于遥感反演水深数据的测图技术研究[J]. 测绘科学, 2009, 34(4): 180-181. |
| [6] |
张晓冬, 张文静, 朱首贤, 等. 海口湾可见光遥感测深方法研究[J]. 海洋通报, 2016, 35(1): 54-63. |
| [7] |
ALPERS W, HENNINGS I. A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar[J]. Journal of Geophysical Research Oceans, 1984, 89(C6): 10529-10546. DOI:10.1029/JC089iC06p10529 |
| [8] |
黄韦艮, 傅斌, 周长宝, 等. 星载SAR遥感浅海水下地形的最佳海况模拟仿真[J]. 自然科学进展:国家重点实验室通讯, 2000, 10(7): 642-649. |
| [9] |
范开国, 黄韦艮, 贺明霞, 等. SAR浅海水下地形遥感研究进展[J]. 遥感技术与应用, 2008, 23(4): 479-485. |
| [10] |
滕惠忠, 熊显名, 李海滨, 等. 遥感水深反演海图修测应用研究[J]. 海洋测绘, 2009, 29(6): 21-25. DOI:10.3969/j.issn.1671-3044.2009.06.006 |
| [11] |
叶安乐, 李凤岐. 物理海洋学[M]. 山东青岛: 青岛海洋大学出版社, 1992.
|
| [12] |
PLESKACHEVSKY A, LEHNER S, HEEGE T, et al. Synergy and fusion of optical and synthetic aperture radar satellite data for underwater topography estimation in coastal areas[J]. Ocean Dynamics, 2011, 61(12): 2099-2120. DOI:10.1007/s10236-011-0460-1 |
| [13] |
DANILO C, MELGANI F. Wave period and coastal bathymetry using wave propagation on optical images[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(11): 6307-6319. |
| [14] |
BELL P. Shallow water bathymetry derived from an analysis of x-band marine radar images of waves[J]. Coastal Eng, 1999, 37: 513-527. DOI:10.1016/S0378-3839(99)00041-1 |
| [15] |
LYU L, CHANG H. Remotely sensing in detecting the water depths and bed load of shallow waters and their changes[J]. Ocean Engineering, 2005, 32(10): 1174-1198. DOI:10.1016/j.oceaneng.2004.12.005 |
| [16] |
陈台颖.频谱分析应用与决定卫卫星影像中的波向及水深推估[D].台湾新竹: 台湾交通大学, 2013.
|
| [17] |
柯绅彦.应用卫卫星影像决定波向线及估算水深之初步探讨[D].台湾新竹: 台湾交通大学, 2012.
|
| [18] |
LI J, ZHANG H, HOU P, et al. Mapping the bathymetry of shallow coastal water using single-frame fineresolution optical remote sensing imagery[J]. 海洋学报(英文版), 2016, 35(1): 60-66. |
| [19] |
POUPARDIN A, IDIER D, MICHELE M D, et al. Water Depth Inversion From a Single SPOT-5 Dataset[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(4): 2329-2342. |
| [20] |
傅斌, 黄韦艮, 周长宝, 等. 星载SAR浅海水下地形和水深测量模拟仿真——水下地形高度、坡度和方向与可测水深分析[J]. 海洋学报, 2001, 23(1): 35-42. DOI:10.3321/j.issn:0253-4193.2001.01.005 |
| [21] |
KUO Y Y, LYU L G, KAO I L. Directional spectrum analysis and statistics obtained from ERS-1 SAR wave images[J]. Ocean Engineering, 1999, 26(11): 1125-1144. DOI:10.1016/S0029-8018(98)00058-4 |
| [22] |
KIRBY J T, WEI G, CHEN Q, et al. Funwave 1.0: Fully nonlinear boussinesq wave model-documentation and user's manual[R]. DE: University of Delaware, 1998.
|
| [23] |
SHI F Y, KIRBY J T, TEHRANIRAD B, et al. FUNWAVE-TVD, documentation and users' manual (CACR-11-03)[R]. DE: University of Delaware, 2011.
|
| [24] |
BERKHOFF J C W, BOOY N, RADDER A C. Verification of numerical wave propagation models for simple harmonic linear water waves[J]. Coastal Engineering, 1982, 6(3): 255-279. DOI:10.1016/0378-3839(82)90022-9 |
| [25] |
王颖. 黄海陆架辐射沙脊群[M]. 北京: 中国环境科学出版社, 2002.
|
| [26] |
陈玮彤, 张东, 施顺杰, 等. 江苏中部淤泥质海岸岸线变化遥感监测研究[J]. 海洋学报, 2017, 39(5): 138-148. DOI:10.3969/j.issn.0253-4193.2017.05.013 |




