2. 软件新技术与产业化协同创新中心, 南京 211106;
3. 江苏易图地理信息科技股份有限公司, 江苏 扬州 225000
2. Collaborative Innovation Center of Novel Software Technology and Industrialization, Nanjing 211106, China;
3. Jiangsu Easymap Geographic Information Technology Corp. Ltd, Yangzhou Jiangsu 225000, China
互联网技术的飞速发展以及电子商务的广泛应用, 信息过载问题变得日益严重[1-2].为了分析用户偏好以及有针对性地向用户进行商品推荐, 大量的推荐算法及相关系统应运而生.从用户角度出发, 有上下文感知推荐系统[3]、移动推荐系统[4]等, 这些推荐系统大多是根据用户的偏好进行商品推荐.然而从商家的角度考虑, 商家更希望的是将销售产量较低而且没有普及的产品推广给用户, 实现多元化商品战略. "长尾理论"完美地解释了这一问题:如果商品的流通方式及商品存量足够多, 普及度较低的商品所带来的收益较热门商品更多, 即商品的销售量不在长尾分布曲线上的头部, 而是在更需要被推广的长尾尾部.因此位于尾部的商品有更大的价值挖掘空间, 位于尾部靠前的商品有较大的价值潜力而且普及度也较高, 有进一步被推广的价值[5].以电影为例, 较为流行的电影都附有动作、喜剧、科幻等特性, 但是纪录片并不带有这些属性, 所以大多数人认为纪录片枯燥无味, 只有少数那些热爱历史的人会关注它, 因此纪录片的普及度并不高.如果将这种电影推广给更多的消费者, 让更多的消费者去了解历史, 关注历史, 从而喜欢上纪录片, 此时纪录片就不再是"偏门电影".由此可见, 对小众中的大众商品进行进一步挖掘是能够发现其原始价值的.出于这一目的, 本文着重研究发掘小众商品中的大众并推荐给用户, 从而提高位于尾部商品的销量并让商品销售多样化, 同时结合幂律对推荐算法进行了改进.
众多领域存在幂律分布现象, 其遍布于经济学、地理学、计算机科学等领域.对幂律分布研究做出重要贡献的是Zipf和Pareto. Zipf发现单词出现的次数与它的频率排名常数成反比; Pareto通过分析社会财富分布现象, 发现大部分财富掌握在少数人手里, 即80-20准则. Zipf定律和Pareto定律是幂律分布的典型代表[6].
已有的推荐系统利用Top-
本文的主要贡献如下.
(1) 总结了传统的偏好预测模型, 提出了基于新标准的专家偏好预测机制以及专家用户提取算法.采用标签连续化的策略将商品和用户映射到空间.
(2) 由于长尾分布是一种典型幂律分布, 提出的推荐算法主要是为了有效缓解"尾大"现象.为寻求幂律分布中的某一阈值点, 将头部忽略, 重点研究尾部的商品, 将原始庞大的商品信息进行范围缩减, 即对查询工作所需要的原始数据集进行范围缩小, 间接地减少了搜索查询算法的时间及空间耗费.
(3) 将RFN的空间数据库查询思想与推荐系统相结合, 对用户进行
本文后续结构是:第1节介绍相关工作; 第2节形式化一系列相关问题; 第3节介绍专家用户的提取、商品标签属性连续化、如何进行幂律的判断, 以及求解相关参数和利用幂律优化查询空间, 构建基于RFN的推荐系统; 第4节是实验与分析; 第5节是结论.
1 相关工作 1.1 偏好预测Goldbeg等人提出的协同过滤(Collaborative Filtering, CF)方法[13]开创了推荐系统的新思路, 大多数推荐系统对于用户偏好预测一般都采用这种协同过滤的方法. Sarwar等人提出了基于物品的协同过滤算法[14], Peng等人对传统的协同过滤算法进行了改进[15].所谓协同过滤主要是通过相似度计算, 将相似度较高的对象来近似代表目标对象的偏好属性.协同过滤主要分为基于用户的协同过滤[16](User-Based Collaborative Filtering, UBCF)和基于物品的协同过滤[17](Item-Based Collaborative Filtering, IBCF). UBCF的基本思想是寻找与目标用户相似度最高的用户群体, 通过分析此用户群体的偏好对目标用户进行推荐. IBCF就是寻找与目标用户喜欢的物品相似的物品, 然后把相似的物品推荐给目标用户. Vozalis等人通过实验对比了这两种协同过滤策略[18], 发现不管是UBCF还是IBCF都涉及相似度的计算.在基于用户的推荐系统中, 用户之间的相似度计算公式为
| $ \begin{equation} {\rm sim}(u, e)=\frac{\sum\limits_{s\in S_{u, e} } {(R_{u, s} -\overline {R}_u)(R_{e, s} -\overline{R}_u )} }{\sqrt {\sum\limits_{s\in S_{u, e}} {(R_{u, s} -\overline{R}_u )^2\times \sum\limits_{s\in S_{u, e}} {(R_{e, s} -\overline{R}_u )^2} } } }, \end{equation} $ |
其中,
通过相似度计算可以得到与目标用户相似的用户集合.基于物品的协同过滤的相似度计算方法和上述类似, 在此不再赘述.
1.2 商品标签属性连续化目前, 基于标签的推荐系统在各类网站尤其是社交、音乐、视频等网站得到了广泛应用.例如将标签与社会关系相结合应用于微博的推荐[19], 通过标签对物品的内容、特征进行准确描述.文献[20]是基于标签个性化的推荐研究, 提出了融合标签流行度、时间权重以及矩阵分解的推荐算法.本文推荐算法在对用户进行个性化推荐时, 需要用户及推荐物品的标签属性信息, 例如推荐电影, 电影是有类别的, 如动作片、喜剧片、爱情片等这些是电影所具有的标签.在进行标签标记时, 某一物品是否带有某个属性通常以0, 1表示, 比如电影Star Wars是否为动作片, 1表示该电影属于动作片, 0表示该电影不是动作片, 没有动作片的特点; 但是0, 1离散化表示不能体现商品附有某种属性的程度, 因此应该将商品属性进行标签值连续化.比如Star Wars电影的Action属性值为0.5 (一般用0
(1) 可以表示某种商品附有某种属性的程度, 不再是单一选择的形式, 当用户想要附带某种属性的商品时, 选择了该属性标签为1的商品, 如果用户体验之后感到这种属性并不明显, 这种推荐效果可能就有点差强人意.运用了连续化的标签后, 可以很直观地了解该商品带有某种属性色彩的程度, 便于用户更好地进行选择.
(2) 将属性标签连续化后, 可以将商品抽象为空间中的点, 例如某种商品有
目前许多研究工作者在自然科学现象中发现了众多服从幂律分布的现象, 例如Faloutsos等人研究了互联网的拓扑结构, 并且发现了互联网路由节点间的度数服从幂律分布[21]; Clementi等人探索发现了意大利居民收入呈现幂律分布的态势[22]; Newman等人将Zipf定律和Pareto定律和幂律进行了比较与总结[23]; Clauset等人利用经验模型对幂律的相关参数进行了预估评判[24].本文主要是利用幂律进行原始数据集的过滤, 将过滤后的数据集根据其属性进行空间化处理, 然后利用空间查询策略进行筛选, 选出符合用户偏好的推荐结果.
近年来空间距离查询策略已经被大量研究, 这些查询可以被概括为以下几种类型:最近邻居和
传统的基于用户的协同过滤算法是通过用户–项目评分表来计算用户相似度, 如果用户集的数量巨大, 对于新加入的用户需要计算和每个老用户的相似度就变得十分复杂.如果能选出一批有代表性的用户, 当新用户加入时, 首先与这些代表性的用户计算相似度, 然后再进行偏好预测可以减少计算时间.本文用专家用户来代表这些代表性用户.
定义1 (专家用户)在推荐系统[26]中, 当用户满足以下3个条件, 这样的用户被称为专家用户.
(1) 用户在其擅长领域相对于大部分用户有更高的活跃度, 并且会对该领域给出更多的评价.
(2) 用户相对于大部分用户有更高的专业性, 并且他们给出的评价一般比较准确.
(3) 用户在社交领域相对于大部分用户有更高的声誉值, 即有较多信任他们的用户.
定义2 (属性专家用户)对于用户
计算用户
| $ \begin{align} {\rm sim}(u, e)=\frac{\sum\limits_{s\in S_{u, e} } {(R_{u, s} -\overline {R}_u )(R_{e, s} -\overline{R}_u )} }{\sqrt {\sum\limits_{s\in S_{u, e} } {(R_{u, s} -\overline{R}_u )^2\times \sum\limits_{s\in S_{u, e} } {(R_{e, s} -\overline{R}_u )^2} } } }\times \frac{2\vert I_{u, e} \vert }{\vert I_u \vert +\vert I_e \vert }, \end{align} $ | (2) |
其中,
| $ \begin{align} R_{u, i} =\overline {R}_u +\frac{\sum\limits_{e\in E_{{u}, k} } {[{\rm sim}(u, e)\times (R_{e, i} -\overline {R}_e)]} }{\sum\limits_{e\in E_{u, k} } {\vert {\rm sim}(u, e)\vert } }, \end{align} $ | (3) |
其中,
在计算用户与专家的相似度之前需要知道哪些用户是专家用户, 因此本文提出如下几个衡量标准.
(1) 活跃度:普通用户和专家用户的区别之一在于专家用户在某些方面的专业知识是非常丰富的.所以专家用户的评价是比较公认及准确的, 用户的活跃度与用户评价的商品数量成正比.计算用户的活跃度的公式为
| $ \begin{align} {\rm ACT}(u)=\frac{N(u)}{N(U)}, \end{align} $ | (4) |
其中,
(2) 准确性:普通用户和专家用户的另一个区别在于专家用户对商品评价的准确程度通常高于普通用户, 即专家评分与物品的平均评分几乎相同.为了衡量用户评分的准确性, 首先需要知道物品
| $ \begin{equation} \overline {R}_i =\frac{1}{N}\times \sum\limits_{u=1}^N {R_{u, i} } \end{equation} $ | (5) |
得出, 则用户对每件商品的评分偏差为
| $ \begin{align} D(R_{u, i} )=1-\frac{\vert R_{u, i} -\overline {R}_i \vert }{\sum\limits_{j=1}^N {\vert R_{u, j} -\overline {R}_j \vert } }. \end{align} $ | (6) |
将式(6)得到的评分偏差取平均值, 并将其用来表示用户评分的准确性, 公式为
| $ \begin{align} C(u)=\frac{1}{M}\sum\limits_{i=1}^M {D(R_{u, i} )} , \end{align} $ | (7) |
其中
(3) 声誉值:普通用户和专家用户的第三个区别在于专家用户在整个社交网络中具有较高的声誉, 即有信任他们的用户较多.用信任用户
| $ \begin{align} R(u)=\frac{M_u }{M_{\max } }. \end{align} $ | (8) |
有了以上3个衡量标准, 本文采用公式
| $ \begin{equation} {\rm EVAL}(u)={\alpha \times {\rm ACT}(u)}+\beta \times C(u)+\gamma \times R(u) \end{equation} $ | (9) |
来评估专家用户.式(9)中
对于用户集合
假设
定义3 任意点
定义4
表 1所示为本文所用到的符号及其定义.
| 表 1 符号定义 Tab. 1 Symbol definition |
第2节的定义1对专家用户进行了定义, 本节将进行专家用户提取以及对商品属性进行连续空间映射化.
3.1 专家用户提取算法对于新用户, 系统并不知道其偏好, 只能通过协同过滤的方式找到其最近的邻居, 通过其最近邻居的偏好来预测该新用户的偏好.
本文对新用户进行相似度计算, 寻求
对商品属性标签进行连续化处理时, 本文采用属性专家用户的方式将离散化的标签变为连续化的标签.为了更清楚地展示本文所做的工作, 主要以电影为例进行说明.
3.2.1 属性专家用户的获取在推荐系统当中, 当拥有了用户
| 算法1: EEA |
| 输入:用户 |
| 输出:专家用户集合EU |
| 1. EU |
| 2. for |
| 3. ACT |
| 4. accuracy_rate |
| 5. if EVAL(u) |
| 6. EU.add |
| 7. end if |
| 8. end for |
| 9. return EU//专家用户集合返回 |
首先需要获取用户的类型矩阵UTM, 通过UTM对用户进行详细的定义. 表 2截取了评分矩阵中部分关于用户A (UserA)的评分记录, UserA对表 2中的5部电影有过观赏并给出了相关评价.结合离散化电影标签属性, 可以得到用户的类型矩阵UTM, 如表 3所示.
| 表 2 UserA的电影评分记录 Tab. 2 UserA's movie rating matrix |
| 表 3 UserA的用户类型矩阵UTM Tab. 3 UserA's user type matrix UTM |
对表 3而言, Total这一行即为UserA对类型的偏好向量UTV, 如果在电影推荐场景中, 所设置的最低属性专家用户可靠度
对于一个用户集合
当需要对一个物品的某一属性标签进行衡量评判时, 该领域的专家对该物品的意见往往具有参考价值.通过对用户
首先, 获取需要被属性空间连续化物品
| $ \begin{equation} a_{u, i, a} =\frac{\max \_{\rm rating}\times R_{u, i} +\min \_{\rm rating}\times R_{u, i} }{4\times\overline {R}_{u, a} } \end{equation} $ | (10) |
获取用户对物品
因为不同用户之间的打分尺度会有所不同, 有些用户习惯打高分, 而有些用户习惯打低分, 为了防止这种情况影响判定结果, 用式(10)将每个用户的评分做统一化的处理; 得到expert_set
| $ \begin{align} {\rm ca}_{i, a} =\sum\limits_{u\in \exp {\rm ert}\_{\rm set}_{i, a} } {\frac{R_{u, i} }{\max \_{\rm rating}\_a\times \overline {R}_{u, a} \vert \exp {\rm ert}\_{\rm set}_{i, a} \vert }}, \end{align} $ | (11) |
其中, ca
基于式(11), 便可将物品
| 算法2: DASC算法 |
| 输入:用户-物品评分矩阵 |
| 输出:物品 |
| 1. U |
| 2. for a |
| 3. if DAV |
| 4. CAV |
| 5. else |
| 6. expert_set |
| 7. if |
| 8. |
| 9. for |
| 10. ca |
| 11. ca |
| 12. else |
| 13. ca |
| 14. for every |
| 15. ca |
| 16. end for |
| 17. end if |
| 18. CAV |
| 19. end if |
| 20. end for |
| 21. return CAV |
以电影为例, 经属性标签连续化后如表 4所示.
| 表 4 电影的连续型属性向量CAV Tab. 4 The continuous attribute vector (CAV) of the film |
因此, 经过属性连续化后的商品信息向量可以映射到空间中.空间坐标的维数和商品属性类型的数量相等, 并且每个属性值表示相应的坐标轴上的值.为了更清晰地表达本文所做的工作, 在此采用了以电影为例而进行说明分析, 以上工作并不仅仅针对电影, 标签连续化策略以及专家用户的提取普适于商品的相关研究.
3.3 推荐结合幂律由于原始商品信息复杂而且庞大, 增加了查询算法的执行时间, 因此需要将原始商品信息中的大众商品剔除, 留下小众商品, 进而选取小众中的大众商品推荐给用户.本文利用幂律来对商品信息进行过滤.
3.3.1 幂律判断幂律分布的概率密度函数为
文献[27]通过训练经验数据得出了幂律分布相关的模型.幂律分布的概率密度函数为
| $ {p}(x) =\frac{\alpha -1}{{x}_{\rm min}}\left(\frac{x}{x_{\min }}\right)^{-\alpha}, $ | (12) |
| $ {p}(x\vert\alpha) =\prod\limits_{i=1}^n {\frac{\alpha {-1}}{{x}_{\rm min}}\left({\frac{x_i }{x_{\min }}}\right)^{-\alpha }}. $ | (13) |
本文采用最大似然估计来求解幂律指数.当对函数采用最大似然估计(Maximum Likelihood Estimation, MIE)后, 函数和取对数后的函数极大值点是相同的, 有
| $ \begin{align} L=\ln p(x\vert \alpha )&=\ln \prod\limits_{i=1}^n {\frac{\alpha -1}{x_{\min } }\Big( {\frac{x_i }{x_{\min } }}\Big)^{-\alpha }} \nonumber\\[2mm] & =\sum\limits_{i=1}^{\rm n} {\Big[ {\ln (\alpha -1)-\ln x_{\min } -\alpha \ln \frac{x_i }{x_{\min } }} \Big]} \nonumber\\[2mm] & =n\ln (\alpha -1)-n\ln x_{\min } -\alpha \sum\limits_{i=1}^n {\ln \frac{x{ }_i}{x_{\min } }}. \end{align} $ | (14) |
通过对
| $ \begin{equation} \widehat{\alpha} =1+n\Big[ {\sum\limits_{i=1}^n {\ln \frac{x_i }{x_{\min } }} } \Big]^{-1}. \end{equation} $ | (15) |
最后得到近似求解
式(15)中
为了有效缩减原始数据空间, 本文通过寻找一个阈值, 以此阈值为界限对商品进行范围缩减, 后续工作只需对缩减后的商品选取
评论时间间隔越长, 则间接表明商品的流行度越低.为了对小众中的大众商品进行推荐, 首先应选取评论间隔时间较长的商品, 然后针对这些商品再选取时间间隔较短的商品进行推荐.所以应该合理选取这个阈值点. 图 1为幂律分布曲线.
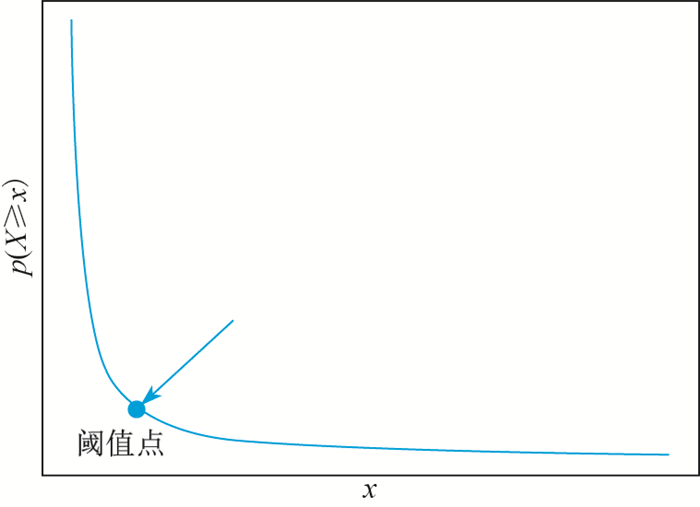
|
图 1 幂律分布曲线 Fig.1 Power law distribution curve |
由于曲率表示曲线的变化程度, 曲率越大, 曲线的弯曲程度变化越大.因此, 曲率最大的点可以用来表示阈值, 有
| $ \begin{equation} \rho =\frac{1}{k}=\frac{[1+(f')^{2}(t)]^{\frac{3}{2}}}{{\vert f"(t)\vert}}, \end{equation} $ | (16) |
其中,
前面已经将商品属性进行了标签连续化, 并且将处理后的商品信息向量映射到了空间中.为了利用空间搜索算法向用户推荐商品, 也将用户进行空间映射化, 可用公式
| $ \begin{equation} P_{u, k} =\frac{\sum\limits_{i=1}^M {R_{u, i} \times } I_{i, k} }{M} \end{equation} $ | (17) |
对用户偏好进行标签连续化.公式(17)中,
在第3.2和第3.4节中, 已将商品和用户进行了空间化的处理, 将商品和用户映射为
表示用户偏好和商品属性之间匹配程度
| $ \begin{align} MC=\frac{1}{\sqrt {\sum\limits_{i=1}^n {(u_i -p_i )^2} } }, \end{align} $ | (18) |
其中,
| 算法3: RUPRA算法 |
| 输入:经连续空间化的用户集合 |
| 输出:推荐列表 |
| 1. L |
| 2. for i |
| 3. UPC( |
| 4. end for |
| 5. for i |
| 6. Ii.knn |
| 7. for k |
| 8. if Uk |
| 9. Lk.add( |
| 10. end if |
| 11. end for |
| 12. end for |
| 13. return |
通过上述算法, 就得到了推荐给用户的商品列表集合.
4 实验结果及分析 4.1 实验数据集本实验选用MovieLens 100k数据集, 其中包括943个用户和1 682部电影的相关信息, 以及100 000条用户对电影的评分记录, 评分结果采用5等级制(1
实验采用的评估方法是机器学习中常见的leave-one-out方法.先将已有的用户偏好隐藏起来, 然后利用推荐系统对该用户偏好进行预测后, 进行商品推荐, 根据推荐商品的平均属性与已有的用户偏好的差距来对推荐系统进行评估.采用平均绝对误差MAE(Mean Absolute Error)对系统进行评估.假设
| $ \begin{align} {\rm MAE}&=\sum\limits_{i=1}^c {{\vert }p_i -q_i \vert }, \end{align} $ | (19) |
其中
根据公式(19), 评价较多的用户会有比较大的权值, 而数据中的大量评价较少的新用户只有很少的权值.为了平衡所有用户, 本文采用平均绝对用户误差MAUE (Mean Absolute User Error)这个标准, 即对每个用户计算MAE, 然后进行平均.设
| $ \begin{equation} {\rm MAUE}=\frac{\sum\limits_{u=1}^m {{\rm MAE}_u }}{m}. \end{equation} $ | (20) |
平均绝对用户误差可以更好地反映系统推荐准确性.
4.3 实验结果与分析本实验首先对不同数量的相似邻居和反向
图 2是基于不同数量
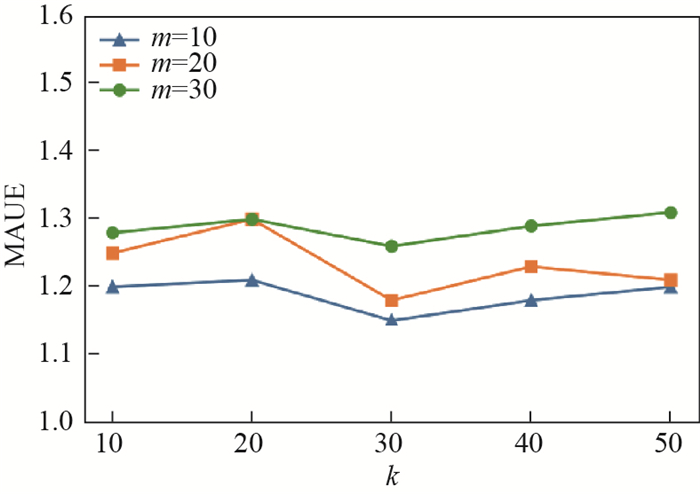
|
图 2 准确性随 |
图 3是基于不同
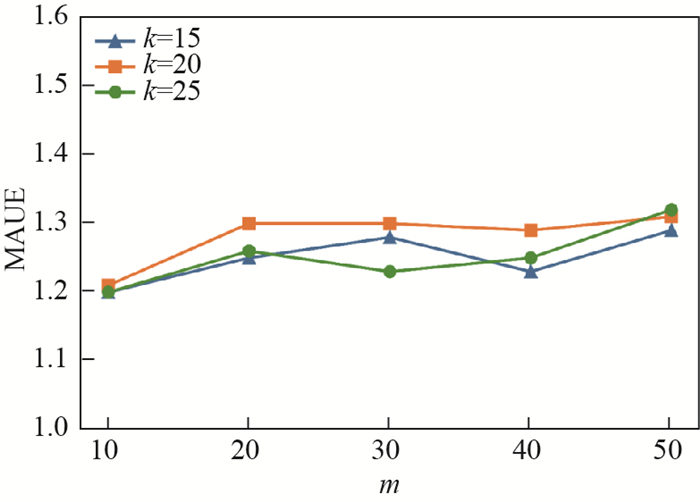
|
图 3 准确性随 |
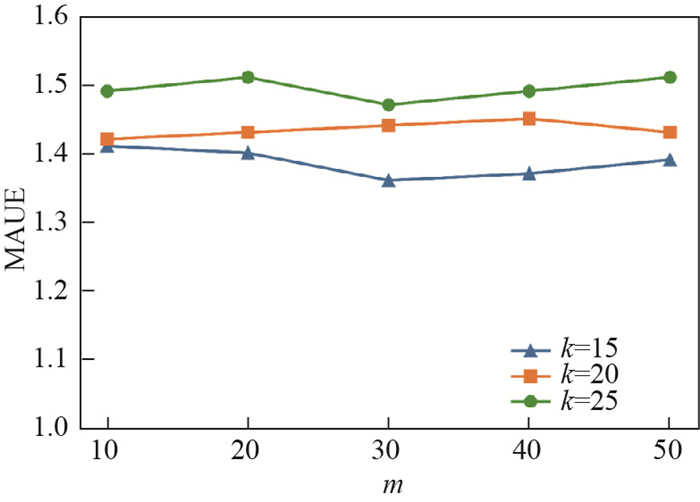
根据第3.3节中的幂律求解方法, 首先从原始数据集中拟合出幂律曲线, 并利用第3.3节中的公式计算其中的参数, 然后利用公式(16)计算出评论时间间隔阈值点, 并以此点为界限, 只保留原始数据集中评论时间间隔大于此阈值点的数据(评论时间间隔越短, 说明商品颇为流行, 关注商品且评论的人也比较多; 相反商品的评论间隔越长, 关注的人越少, 商品的流传度越低).通过这种方式来选取原始数据集中的小众商品, 从而挖掘小众商品中有较大潜力的大众商品来进行推荐.实验结果如图 4、图 5所示.
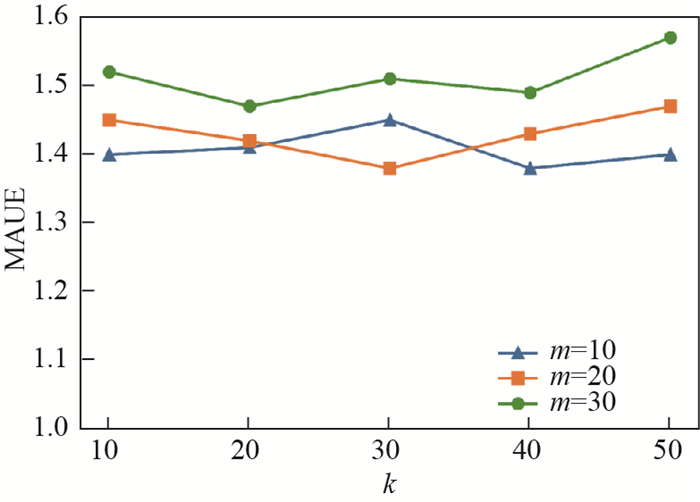
|
图 4 经幂律过滤后准确性变化趋势 Fig.4 Trend of accuracy change after power law filtering |
|
图 5 经幂律过滤后准确性变化趋势 Fig.5 Trend of accuracy change after power law filtering |
图 4、图 5是经过幂律进行过滤后, 将有较大潜力的电影推荐给用户的误差展示, 图 2、图 3和图 4、图 5相比, 图 4、图 5的误差程度明显高于图 2、图 3.因为经过幂律筛选后, 评分较高、口碑较好的电影已经被过滤掉, 剩下的有潜力的电影可能并不是完全符合用户偏好的, 但是拥有值得推荐的价值, 因此误差相对较高.
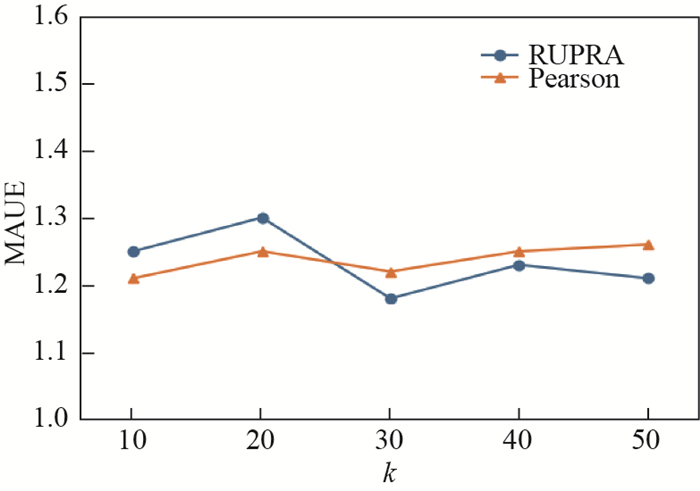
图 6是在最近邻居
|
图 6 本文模型(RUPRA)与Pearson模型准确性对比 Fig.6 Accuracy comparison between the proposed model (RUPRA) and the Pearson model |
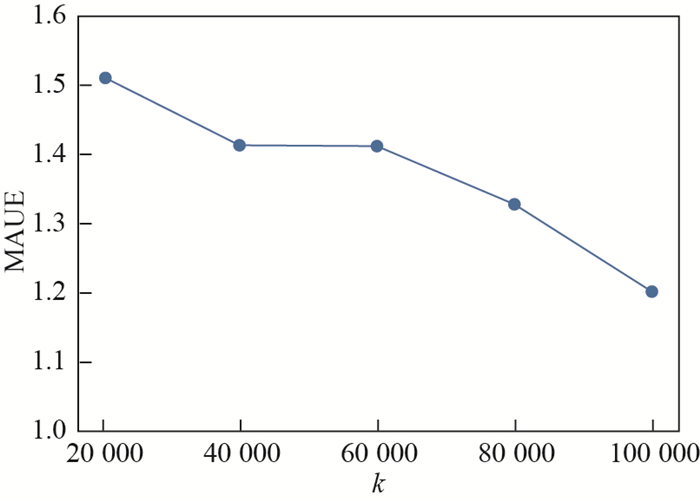
图 7表示在
|
图 7 不同样本数量的推荐算法准确性变化趋势 Fig.7 Accuracy trend of the recommendation algorithm with different sample sizes |
以上分析证明了在不同情况下本文推荐系统(RUPRA)的准确性, 以及不同的近似专家数量、商品的最远用户数量和样本数量对本文推荐系统准确性的影响.
5 结论本文基于传统的协同过滤提出了基于RFN的专家用户协同过滤算法.为了充分挖掘小众中的大众商品的价值潜力, 本文通过幂律对商品信息进行过滤, 同时对商品属性及用户偏好进行空间映射化, 结合空间查询思想向用户进行推荐.实验证明本文的推荐系统准确率较高, 可以让非主流商品吸引更多的目标用户, 实现了对小众中的大众进行推荐, 对推荐系统的应用具有重要意义.
| [1] |
BOBADILLA J, ORTEGA F, HERNANDO A. Recommender systems survey[J]. Knowledge-Based Systems, 2013, 46(1): 109-132. |
| [2] |
XU H L, WU X, LI X D, et al. Comparison study of Internet recommendation system[J]. Journal of Software, 2009, 20(2): 350-363. |
| [3] |
HUSSEIN T. Context-Aware Recommender Systems 2011[C]//ACM Conference on Recommender Systems. ACM, 2011:349-350.
|
| [4] |
MENG X W, XUN H U, WANG L C, et al. Mobile recommender systems and their applications[J]. Journal of Software, 2013, 24(1): 91-108. |
| [5] |
ANDERSON C. The long tail[J]. Wired Magazine, 2004, 12(10): 170-177. |
| [6] |
NEWMAN M E J. Power laws, Pareto distributions and Zipf's law[J]. Contemporary Physics, 2005, 46(5): 323-351. DOI:10.1080/00107510500052444 |
| [7] |
YANG X W, STECK H, GUO Y, et al. On top-k recommendation using social networks[C]//Proceedings of the 6th ACM Conference on Recommender Systems. ACM, 2012:67-74.
|
| [8] |
KHRIBI M K, JEMNI M, NASRAOUI O. Automatic recommendations for e-learning personalization based on web usage mining techniques and information retrieval[C]//Advanced Learning Technologies, 2008, ICALT'08, 8th IEEE International Conference on. IEEE, 2008:241-245. http://www.freepatentsonline.com/article/212768683.html
|
| [9] |
ABEL F, GAO Q, HOUBEN G J, et al. Analyzing user modeling on twitter for personalized news recommendations[C]//International Conference on User Modeling, Adaptation, and Personalization. Berlin:Springer, 2011:1-12. https://link.springer.com/chapter/10.1007%2F978-3-642-22362-4_1
|
| [10] |
YAO B, LI F F, KUMAR P. Reverse furthest neighbors in spatial databases[C]//IEEE, International Conference on Data Engineering. IEEE, 2009:664-675. https://www.researchgate.net/publication/220965425_Reverse_Furthest_Neighbors_in_Spatial_Databases
|
| [11] |
LIU J Q, CHEN H X, FURUSE K, et al. An efficient algorithm for arbitrary reverse furthest neighbor queries[C]//Asia-Pacific Web Conference. Berlin:Springer, 2012:60-72. https://www.researchgate.net/publication/261859969_An_Efficient_Algorithm_for_Arbitrary_Reverse_Furthest_Neighbor_Queries
|
| [12] |
WANG S L, CHEEMA M A, LIN X M, et al. Efficiently computing reverse k furthest neighbors[C]//Data Engineering (ICDE), 2016 IEEE 32nd International Conference on. IEEE, 2016:1110-1121. https://www.researchgate.net/publication/304456743_Efficiently_computing_reverse_k_furthest_neighbors
|
| [13] |
GOLDBERG D, NICHOLS D, OKI B M, et al. Using collaborative filtering to weave an information tapestry[J]. Communications of the ACM, 1992, 35(12): 61-70. DOI:10.1145/138859.138867 |
| [14] |
SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th international conference on World Wide Web. ACM, 2001:285-295. https://www.researchgate.net/publication/2369002_Item-based_Collaborative_Filtering_Recommendation_Algorithms
|
| [15] |
XIAO P, SHAO L S, LI X R. Improved collaborative filtering algorithm in the research and application of personalized movie recommendations[C]//Intelligent Systems Design and Engineering Applications, 20134th International Conference on. IEEE, 2013:349-352. https://www.researchgate.net/publication/271472705_Improved_Collaborative_Filtering_Algorithm_in_the_Research_and_Application_of_Personalized_Movie_Recommendations
|
| [16] |
ZHAO Z D, SHANG M S. User-based collaborative-filtering recommendation algorithms on hadoop[C]//20103rd International Conference on Knowledge Discovery and Data Mining. IEEE, 2010:478-481. https://www.researchgate.net/publication/221306166_User-Based_Collaborative-Filtering_Recommendation_Algorithms_on_Hadoop
|
| [17] |
PIRASTEH P, JUNG J J, HWANG D. Item-based collaborative filtering with attribute correlation:A case study on movie recommendation[C]//Asian Conference on Intelligent Information and Database Systems. Cham:Springer, 2014:245-252. https://link.springer.com/chapter/10.1007%2F978-3-319-05458-2_26
|
| [18] |
VOZALIS E G, MARGARITIS K G. Recommender systems:An experimental comparison of two filtering algorithms[C]//Proceedings of the 9th Panhellenic Conference in Informatics-PCI 2003. 2003.
|
| [19] |
MA H F, JIA M H Z, ZHANG D, et al. Combining tag correlation and user social relation for microblog recommendation[J]. Information Sciences, 2017, 385/386: 325-337. DOI:10.1016/j.ins.2016.12.047 |
| [20] |
郭娣, 赵海燕. 融合标签流行度和时间权重的矩阵分解推荐算法[J]. 小型微型计算机系统, 2016, 37(2): 293-297. DOI:10.3969/j.issn.1000-1220.2016.02.019 |
| [21] |
FALOUTSOS M, FALOUTSOS P, FALOUTSOS C. On power-law relationships of the internet topology[J]. ACM SIGCOMM Computer Communication Review, 1999, 29(4): 251-262. DOI:10.1145/316194 |
| [22] |
CLEMENTI F, GALLEGATI M. Power law tails in the Italian personal income distribution[J]. Physica A:Statistical Mechanics and its Applications, 2005, 350(2/3/4): 427-438. |
| [23] |
NEWMAN M E J. Power laws, Pareto distributions and Zipf's law[J]. Contemporary physics, 2005, 46(5): 323-351. DOI:10.1080/00107510500052444 |
| [24] |
CLAUSET A, SHALIZI C R, NEWMAN M E J. Power-law distributions in empirical data[J]. SIAM review, 2009, 51(4): 661-703. DOI:10.1137/070710111 |
| [25] |
LI B H, ZHANG C, CHEN W H, et al. Dynamic reverse furthest neighbor querying algorithm of moving objects[C]//ADMA 2016:Advanced Data Mining and Applications. Cham:Springer, 2016:266-279. http://en.cnki.com.cn/Article_en/CJFDTotal-XXWX201606003.htm
|
| [26] |
郑伟, 李博涵, 王雅楠, 等. 融合偏好交互的组推荐算法模型[J]. 小型微型计算机系统, 2018, 2(39): 372-378. |
| [27] |
CLAUSET A, SHALIZI C R, NEWMAN M E J. Power law distributions in empirical data[J]. SIAM Review, 2009, 51(4): 661-703. DOI:10.1137/070710111 |
| [28] |
高珂. 基于消费者行为分析的电子商务市场研究[D]. 山东青岛: 青岛理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10429-1011302212.htm
|




