众所周知,连通图在通信网络、社交网络、交通网络等有着广泛的应用[1-2]. 例如: 在通信网络中,即所有可能的信息传输线路构成的图中,点代表发射机,连接各点的边代表通信线路,或许网络中发射机的可靠性很高以至于不会瘫痪,但是通信线路可能会受到噪音干扰或其他干扰从而中断连接[3-5]. 介于这种情况,人们希望网络不会因为删除了某些连接而变得不稳定、不连通 (如通讯中断、交通瘫痪等). 在数学的分支图论中,连通图占据着十分重要的研究地位,因此对连通图的深入研究不仅是数学理论的需要,同时更重要的是为研究实际网络结构提供可靠的理论依据和可行的技术手段. 本文以2-边连通图为例展开讨论,研究2-边连通图的结构并描述2-边连通图的特征.
关于2-边连通图的充分必要条件可以在许多文献中看到. West在他的书[6]中给出了2-边连通图的6种等价性命题. Bondy和Murty在他们的书[7]中,给出了关于2-边连通图特征的4个等价性命题. 这些相互等价的命题是从不同的角度来刻画2-边连通图. 本文整理了有关2-边连通图的若干充分必要条件,也为收集到的若干充分必要条件提供较为简单的证明. 更为重要的是,本文对2-边连通图定义了2种新运算,分别是割点均匀剖分运算和反三角形边收缩运算,由此两种运算得到了2个新定理,本文分别给出了它们的证明.
1[7] 图G的边割E*是图G的边子集,使得图G-E*的分支数目大于图G的分支数目. 一个k边割是指包含k条边的边割. 图G的所有k边割中最小的k称为图G的边连通度. 若图G的边连通度大于等于k,则称图G为k-边连通的.
2[6] 图G的一个耳朵是指图G中内部顶点的度数均为2的极大路. 图G的闭耳是图G中除一个顶点外其他顶点的度均为2的一个圈. 图G的一个耳边分解是满足下面条件的分解
3[6] 一条(u,v)-链是一系列圈C1,C2,… ,Ck,使得

|
图 1 一条 (u,v)-链 Fig.1 A (u,v)-chain |
4[6] 对图G的一个顶点x和一个顶点子集U,一个(x,U)-迹扇是指从x到U的每个顶点的迹构成的集合,且此集合中任意2条迹在图G中无公共边(示例见图 2).
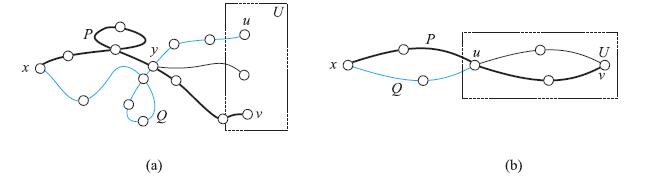
|
图 2 (a)一个(x,U)-迹扇,粗线是 (x,v)-迹 P,蓝色线 是 (x,u)-迹 Q;(b)一个特殊的 (x,U)-迹扇,(x,v)-迹必须通过顶点 u Fig.2 (a) An (x,U)-trail fan,where the (x,v)-trail P is in thick line,the (x,u)-trail Q is blue line; (b) An (x,U)-trail fan,but any (x,v)-trail must pass the vertex u |
5[6] 设图G是无割边的连通图,图G的块分解是指图G含有边不交的块
文献[7]给出如下的概念: 没有割点的连通图称为块. 若顶点与边的交错链
顶点均匀剖分运算是指: 对任意度数不小于4的顶点
不难看到,对顶点u实施顶点均匀剖分运算后,顶点u'和顶点u''的度数之和是原来顶点u的度数加2. 图 3给出了顶点均匀剖分运算的一个例子,即对图 3(a)所示的图G的顶点y和顶点w实施均匀剖分运算,得到图 3(b)所示的图H.
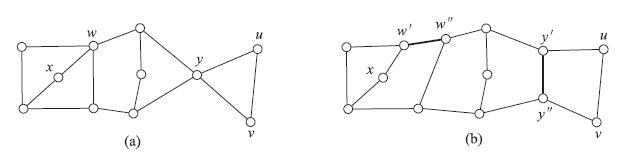
|
图 3 (a)图G; (b)图H Fig.3 (a) Graph G; (b) Graph H |
定理 1 图G是2-边连通图当且仅当对图G中的每一个割点作均匀剖分运算所得新图是2-连通图 (示例见图-3).
证明 必要性 设图G是2-边连通图,图G的所有割点为
充分性 对图G中的每一个割点
2-连通图一定是2-边连通图,但2-边连通图不一定是2-连通图. 本文对2-边连通图定义了顶点均匀剖分运算,定理1使得非2-连通的连通图可以转化为2-连通图,使得2-连通图的若干性质与2-边连通图的若干性质可以对应起来,方便人们深入研究它们的性质. 下面列出2-边连通图的若干等价命题. 为了不与2-连通图的命题重复,以下总假定讨论的图有割点.
定理 2 设图G是无割边、有割点的连通图. 下面的命题相互等价.
(1)[7] 图G是2-边连通图.
(2)[7] 图G有块分解.
(3)[6] 图G的任意2个顶点至少被2条无公共边的迹所连通.
(4)[6] 对任意2个顶点
(5)[6] 图G有一条包含任意2个顶点的闭迹.
(6) 将图G中的路uwv换成边uv后得到的图是2-边连通图,其中w是2度顶点.
(7) 在图G添加一个新顶点w,并将顶点w与G中任意一对顶点u,v分别相连得到的图是2-边连通图.
(8)[6] 对于图G的至少具有2个顶点的子集U和子集U外的一个顶点x,图G有一个(x,U)-迹扇.
(9)[7] 图G的任意一个顶点和任意一条边都位于同一条闭迹上.
(10) 图G有一条最长闭迹T,使得G的任何一条边要么在T上,要么在一条起终点均在T上的(闭)迹上.
(11)[6] 图G有一条包含任意2条边的闭迹.
(12)[7] 对每一对满足顶点个数
(13)[8] 对于图G的任意2个顶点u,v和任意的一条边e,图G有包含边e的(u,v)-迹.
(14)[8] 对于图G的任意3个顶点u,v,w,图G有包含顶点w的(u,v)-迹.
(15)[6] 图G有耳边分解,并且G的每个圈均是图G的某个耳边分解的起始圈.
(16)[8] 对于图G的任意3个顶点u,v和w,图G有不包含顶点w的(u,v)-迹.
(17)[9] 图G的任意2条边都在图G的同一个键中.
证 明 以下用符号
(1)⇒(2). 设图G有k个割点,对图G作块化运算: 设x是图G的一个割点,图
(2)⇒(3). 由命题(2)知,图G存在块分解. 则图G中每一个顶点至少属于一个块. 且块与块之间以图G的割点相互连接. 对于图G中任意2个顶点u,v,若u,v属于图G的同一个块,则在此块中必然存在两条连接u,v且无公共边的路. 若u,v分别属于图G的不同块
(3)⇒(4). 根据命题(3),对于任意的
(4)⇒(5). 根据命题(4),对图G中任意2个顶点u,v,图G中存在一条(u,v)-链. 而(u,v)-链也是一条闭迹,又因为顶点u,v的选取是任意的,故图G的任意2个顶点在图G的一个闭迹中.
(5)⇒(6). 设图G有路uwv,其中w是2度顶点. 根据命题(5),G有一条包含顶点u和w(或顶点v和w)的闭迹P,注意w是2度顶点,那么顶点v必在闭迹P中. 在G中将路uwv换成边uv,则很显然u与v仍然被包含在这个闭迹中. 故新得到的图H是2-边连通的. 有时,图H可能不再是简单图,是有重边的伪图.
(6)⇒(7). 给图G添加一个顶点w,将w与任意选择的一对顶点u和v相连得图H. 若H有割边xy,则
(7)⇒(8). 设U是图G的至少有2个顶点的顶点子集,顶点
(8)⇒(9). 任取图G的一个顶点x和一条边
(9)⇒(10). 设图G的最长闭迹为T,若边e在最长闭迹上,证毕. 若边e不在最长闭迹T上,则取T上的一个顶点u,由命题(9)可知顶点u与边e位于图G的同一条闭迹W上. 若W与T有一个交点,则边e在一条起终点均在T上的闭迹; 若W与T有
(10)⇒(11). 情形1: 若2条边
(11)⇒(12). 设图G的2个顶点子集|X|,|Y|有顶点个数
(12)⇒(13). 对于图G的任意2个顶点u,v和任意一条边
(13)⇒(14). 对图G的任意3个顶点u,v,w,设顶点w是边e的一个端点,由命题(13),知图G中包含边e的(u,v)-迹. 显然,这条迹包含了顶点w,也就是命题(14)得证.
(14)⇒(15). 从图G中的任意一个圈C出发,建立图G的一个耳边分解. 设图
(15)⇒(16). 由命题(15)知,图G存在耳边分解
(16)⇒(17). 任取图G的2条边
(17)⇒(1). 根据命题(17),图G的任意2条边都位于图G的同一个键中. 键为图的最小边割,即说明图G的键中最少有2条边. 这说明图G为2-边连通图.
综上论证,本定理得证.
反三角形边收缩运算: 对
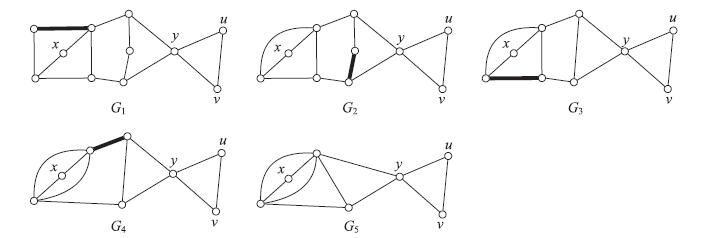
|
图 4 一个反三角形边收缩的例子 Fig.4 An example of the anti-triangle edge contraction |
定理 3 G 是 2-边连通图当且仅当经过一系列反三角形边收缩运算后得到连通图H,使得H是全边三角形图.
证 明 充分性 显然,只要从收缩到最后的全边三角形图H原路返回到图G,且每一个返回步骤产生的图是2-边连通图.
必要性 因为图G是2-边连通图,对G作反三角形边收缩运算时. 因为反三角形边收缩运算不产生割边,边收缩后的图是2-边连通图. 对所有不在三角形中的边进行边收缩运算,直到每条边都包含在某个三角形中时,收缩过程结束. 最终得到的图H是全边三角形图. 显然,H也是2-边连通图.
2 总结
本文给出了若干2-边连通图的等价性命题. 如果对定理2中的等价命题进行两两等价性证明,将要写
本文的创新点在于定理1和定理3,以及定理2中的命题(10). 定理1定义了割点均匀剖分运算,定理3定义了反三角形边收缩运算. 根据定理3,每一个2-边连通图是对某个全边三角形图实施一系列顶点剖分的结果,从而给出一种构造2-边连通图的方法. 定理2的命题(10)研究了2-边连通图的最长闭迹与此图的任一条边之间的位置关系. 以上等价命题从多个角度对2-边连通图的特征进行了刻画. 这里要指出,定理2中的等价命题的相互推证会有其他的简单方案,也就是说,本文的证明方案不一定是最简单的. 基于数学的严谨、优美观点,寻找定理2的最简单的证明方案仍然是一项有意义的工作. 我们不能证明,不存在不同于本文列举的其他的2-边连通图的等价命题.
| [1] | CRUCITTI P, LATORA V, MARCHIORI M, et al. Error and attack tolerance of complex networks[J]. Physica A, 2004, 340: 388-394. DOI:10.1016/j.physa.2004.04.031 |
| [2] | KRAPIVSKY P L, REDNER S, LEYVRAZ F. Connectivity of growing random networks[J]. Phys Rev Lett, 2000, 85(21): 4629-4632. DOI:10.1103/PhysRevLett.85.4629 |
| [3] | YAO B, YANG C, YAO M, et al. Graphs as models of scale-free networks[J]. Applied Mechanics and Materials, 2013, 380: 2034-2037. |
| [4] | YAO B, WANG H Y, YAO M, et al. On the collapse of graphs related to scale-free networks [C]//Proceeding of the 3rd International Conference on Information Science and Technology. 2013: 738-743. |
| [5] | YAO B, LIU X, ZHANG W J, et al. Applying graph theory to the internet of things [C]//2013 IEEE International Conference on High Performance Computing and Communications and 2013 IEEE International Conference on Embedded and Ubiquitous Computing. 2013: 2354-2361. |
| [6] | WEST D B. 图论导论[M]. 北京: 机械工业出版社, 2006. |
| [7] | BONDY J A, MURTY U S R. Graph Theory with Applications[M]. New York: The Macmillan Publishers, 1976. |
| [8] | 高随祥. 图论与网络流理论[M]. 北京: 高等教育出版社, 2009. |
| [9] | DIESTEL R. Graph Theory[M]. 北京: 高等教育出版社, 2012. |




