至2000年第一块超常材料(Metamaterials, MMs)被Smith[1]等人在实验室制备出来以来, 由于它具备负的折射率[2]、负的Goos-Hänche位移[3]、逆多普勒效应等反常物理特性[4], 越来越多的目光投向了对超常介质的物理性质和潜在应用的研究[5].随着越来越多的线性和非线性超常介质被发明, 加速了对电磁波在超常介质中传输的研究[5].这些研究表明了超常介质具有正折射率区(Positive-Index Region, PIR), 吸收区和负折射率区(Negative-Index Region, NIR)[6-7].Wen[8]等人利用Drude模型推导了光脉冲在超常介质中传输的非线性薛定谔方程(Non-Linear Schrodinger Equation, NLSE).而Joseph和Porsezian[9]则利用前者推导的非线性薛定谔方程研究了光脉冲传输的动力学行为.对于超常介质非线性性质的研究则更多, 如自相位调制(Self-Phase Modulation, SPM)、自陡峭(Self-Steepening, SS)[10-14]等等.尽管有许许多多学者对超常介质中不同特性的研究, 但是对于超常介质, 尤其是负折射率材料中高阶色散对于高斯脉冲传输特性影响的研究仍然很少.本文中, 我们将深入地讨论高阶色散对脉冲传输的影响.并结合分析结果进一步进行了色散补偿的研究.
在常规介质中, 往往只考虑二阶色散对群速色散(Group Velocity Dispersion, GVD)效应的影响.超常介质作为一种人工合成材料, 我们发现其中的各阶色散系数在数量级上高于常规介质中相应的色散系数(本文第2节), 这使得在光脉冲传输中不再能忽略高阶色散的影响.本文将讨论超常介质中三阶色散和四阶色散对高斯脉冲传输的影响, 分析脉冲畸变与色散之间的关系, 这一工作对于了解色散的影响以及对色散进行补偿有一定的实际意义.
1 光脉冲在超常介质中传输模型光作为一种电磁波, 在超常介质中传输遵循麦克斯韦方程组, 所以基于麦克斯韦方程组可以推导得到脉冲在非线性色散超常介质中的波动方程
| $\frac{\partial ^2E}{\partial z^2}=\mu _0 \varepsilon _0\frac{\partial ^2E}{\partial t^2}+\mu _0 \frac{\partial ^2P_\mathrm{NL} }{\partial t^2}.$ | (1) |
令
| $\frac{\partial A}{\partial z}=-\frac{\mathrm i}{2}\beta_2 \frac{\partial ^2A}{\partial T^2}+\frac{1}{6}\beta _3\frac{\partial ^3A}{\partial T^3}-\frac{\mathrm i}{24}\beta _4\frac{\partial ^4A}{\partial T^4}-\frac{1}{2}\alpha A+\mathrm i\Gamma _1 \vert A\vert ^2A, $ | (2) |
其中
| $\begin{align} \beta _i =\frac{\mathrm d^ik}{\mathrm d\omega ^i}\Big| _{\omega =\omega _0}\quad (i=1,2,3,\cdots), \end{align}$ | (3) |
| $\begin{align} & \Gamma _1 =\frac{\varepsilon _0 \mu _0 \chi ^{(3)}\omega ^2\mu _\mathrm r (\omega )}{2\beta _0 }, \end{align}$ | (4) |
其中
超常介质中, 相对介电常数
| $\varepsilon _\mathrm r =1-\frac{\omega _\mathrm {pe} ^2}{\omega^2}, \quad \mu _\mathrm r =1-\frac{\omega _\mathrm {pm} ^2}{\omega^2}, $ | (5) |
其中,
| $\begin{align} & \beta _1 =\frac{dk}{d\omega }=\frac{1}{c}\left[{n+\frac{1}{n}\left( {\frac{1+\overline {\omega }_p ^2}{{\overline\omega }^2}}-\frac{2\overline {\omega }_p ^2}{{\overline \omega}^4}\right)}\right], \end{align}$ | (6a) |
| $\begin{align} & \beta _2 =\frac{d\beta _1 }{d\omega }=\frac{1}{c\omega _{pe}}\left[{\frac{1}{n\overline \omega}\left( {-\frac{1}{\overline\omega^2}-\frac{\overline \omega_p ^2}{\overline\omega^2}+6\frac{\overline \omega_p ^2}{\overline \omega^4}}\right)-\frac{1}{n^3\overline \omega}\left( {\frac{1+\overline\omega_p ^2}{\overline \omega^2}-\frac{2\overline \omega_p^2}{\overline \omega^4}} \right)^2} \right], \end{align}$ | (6b) |
| $\begin{align} & \beta _3 =\frac{d\beta _2 }{d\omega }=\frac{1}{c\omega _\mathrm{pe} ^2}\Bigg\{ 3\left[{\frac{1}{n}\left( {-3\frac{1}{\overline\omega^4}-3\frac{\overline \omega_p ^2}{\overline\omega^4}+10\frac{\overline \omega_p ^2}{\overline \omega^6}}\right)-\frac{1}{n^3}\left( {\frac{1+\overline \omega_p^2}{\overline \omega^3}-\frac{2\overline \omega_p ^2}{\overline\omega^5}} \right)^2} \right]\notag\\[2mm] & \ \quad \ +\overline \omega\Bigg[\frac{1}{n}\frac{12\overline \omega_p ^2\overline \omega^2-60\overline \omega_p ^2+12\overline \omega^2}{\overline \omega^7}+\frac{3}{n^5}\left( {\frac{\overline \omega_p ^2\overline\omega^2-2\overline \omega_p ^2 +\overline \omega^2}{\overline\omega^5}} \right)^3 \notag\\[2mm] & \ \quad\ +\frac{3}{n^3}\left( {\frac{\overline \omega_p ^2\overline \omega^2 -2\overline \omega_p ^2+\overline \omega^2}{\overline \omega^5}} \right) \left({\frac{3\overline \omega_p ^2\overline \omega^2-10\overline \omega_p^2 +3\overline \omega^2}{\overline \omega^6}} \right) \Bigg] \Bigg\}, \end{align}$ | (6c) |
| $\begin{align} & \beta _4 =\frac{d\beta _3 }{d\omega }=\frac{1}{c\omega _{pe}^3}\Bigg\{\frac{4\left( {12\overline \omega_p ^2\overline\omega^2-60\overline \omega_p ^2+12\overline \omega^2}\right)}{n\overline \omega^7}-\frac{3\left( {3\overline \omega_p^2\overline \omega^2-10\overline \omega_p ^2+3\overline \omega^2}\right)}{n^3\overline \omega^{11}} \notag\\[2mm] & \ \quad \qquad-\frac{60\overline \omega_p ^2\overline \omega^2-420\overline \omega_p ^2 +60\overline \omega^2) } {n\overline \omega^7}-\frac{15\left( {\overline \omega_p ^2\overline \omega^2 -2\overline \omega_p^2+\overline \omega^2} \right)^4}{n^7\overline \omega^{19}} \notag\\[2mm] & \ \quad \ -\frac{4\left( {\overline \omega_p ^2\overline\omega^2-2\overline \omega_p ^2+\overline \omega^2} \right) \left( {12\overline \omega_p ^2\overline \omega^2-60\overline \omega_p^2+12\overline \omega^2} \right)}{n^3\overline \omega^{11}} \notag\\[2mm] & \ \quad \ -\frac{9\left( {\overline \omega_p ^2\overline\omega^2-2\overline \omega_p ^2+\overline \omega^2} \right)^2\left({6\overline \omega_p ^2\overline \omega^2-20\overline \omega_p^2+6\overline \omega^2} \right)}{n^5\overline\omega^{15}}+\frac{12\left( {\overline \omega_p ^2\overline\omega^2-2\overline \omega_p ^2+\overline \omega^2}\right)^3}{n^5\overline \omega^{15}}\notag \\[2mm] & \ \quad \qquad+\frac{12\left( {\overline \omega_p ^2\overline \omega^2-2\overline \omega_p ^2+\overline \omega^2} \right)\left( {3\overline \omega_p ^2 \overline \omega^2-10\overline \omega_p^2+3\overline \omega^2} \right)}{n^3\overline \omega^{11}} \Bigg\}, \end{align}$ | (6d) |
其中, 归一化光波中心频率
| $\begin{equation} \Gamma _1 =\frac{x^{(3)}\overline {\omega }\omega _\mathrm {pe} (1-\frac{\overline {\omega }_p ^2}{\overline {\omega }^2})}{2nc}\quad . \end{equation}$ | (7) |
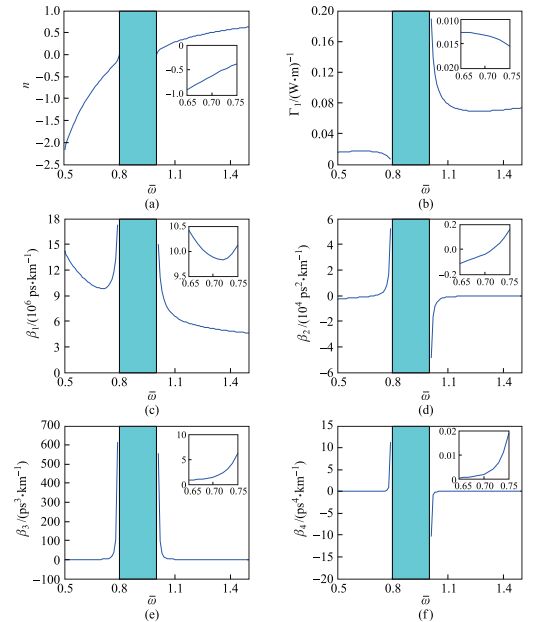
根据色散公式(6) 和三阶非线性系数公式(7) 可以画出色散系数和非线性系数关于归一化频率
|
注:各图中子图为归一化频率为0.7附近的局部放大图
图 1 折射率n、三阶非线性系数和一阶、二阶、三阶、四阶色散系数分别随归一化频率 |
图 1(a)为超常介质中折射率n随归一化频率
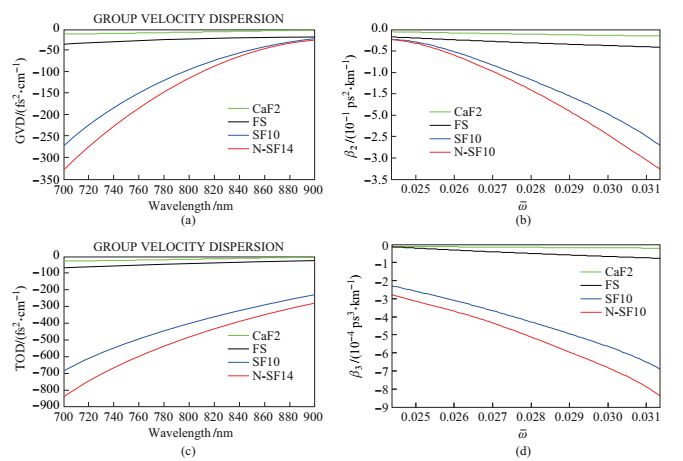
图 2(a)、图 2(c)取自网络[15-16], 展现了四种常规介质的
|
图 2 (a)、(c)分别为几种常规介质的二阶色散和三阶色散随波长变化的曲线图; (b)、(d)为相应的二阶色散和三阶色散随归一化频率变化的曲线图 Fig.2 (a), (c) Second-order and third-order dispersion in several conventional media; (b), (d) The corresponding relationship of (a), (c) with normalized frequency |
本文采用BPM(Beam Propagation Method)(光束传播法)进行脉冲传输仿真.入射脉冲采用具有归一化强度的高斯脉冲
从图 1(d)中, 我们找到了零色散归一化频率
根据图 1(e), 在零色散归一化频率
|
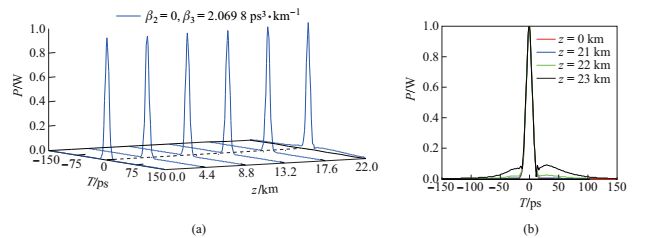
图 3 (a)当 |
从图 3(a)可以看出, 脉冲在出现分裂前(
图 1(d)中, 零色散归一化频率
|
表 1 |
|
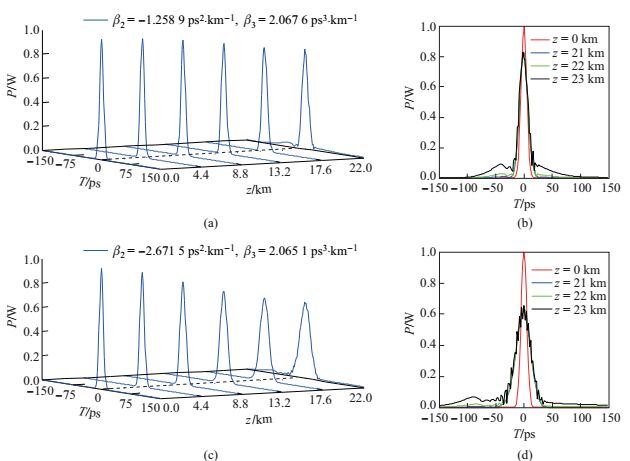
图 4 (a)、(c)相应于表 1中两种情况的高斯脉冲传输图; (b)、(d)为相应的脉冲在不同传输距离的波形对比图 Fig.4 (a), (c) Pulse propagation for two cases in Table 1; (b), (d) Corresponding waveform comparison at different propagation distances |
从图 4(b)、图 4(d)可以看出, 脉冲在22 km处开始出现分裂.但当脉冲出现分裂后, 脉冲继续传输很短距离, 脉冲就会迅速变坏, 次峰峰值和宽度都会迅速增大.同样的, 在上述两种情况下, 三阶色散长度
比较图 3和图 4(d)可以看出, 图 4(d)中脉冲分裂的情形没有图 3严重, 分裂峰的峰值略小且离脉冲主峰更远, 但其实图 4(d)所对应的
图 1(d)中, 零色散归一化频率
|
表 2 |
|
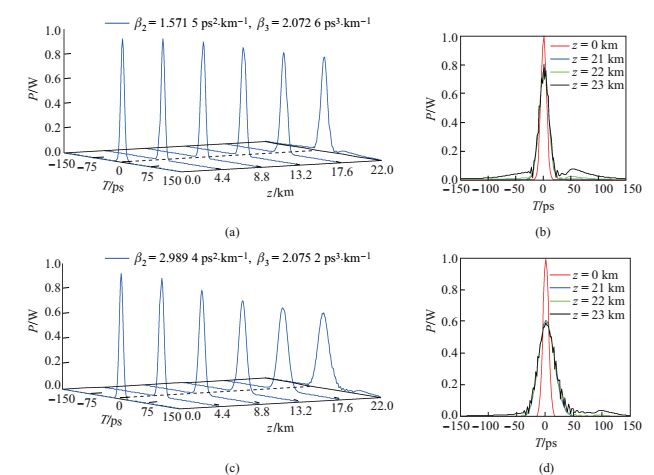
图 5 (a)、(c)相应于表 2中两种情况的高斯脉冲传输图; (b)、(d)为相应的脉冲在不同传输距离的波形对比图 Fig.5 (a), (c) Pulse propagation for two cases in Table 2; (b), (d) Corresponding waveform comparison at different propagation distances |
从图 5(b)也可以看出, 脉冲在22 km处开始出现分裂, 脉冲继续传输很短距离, 脉冲就迅速变坏, 次峰峰值和宽度都会迅速增大.图 5(d)中, 脉冲分裂也是出现在大约22 km, 但是当脉冲传输到22 km时, 脉冲展宽已经很明显; 与图 4情况相似, 虽然三阶色散长度
比较图 3和图 5(d)可以看出, 图 5(d)中脉冲分裂的情形没有图 3严重, 分裂峰的峰值略小且偏离脉冲主峰更远, 但其实图 5(d)所对应的
在常规介质中, 由于
|
表 3 |
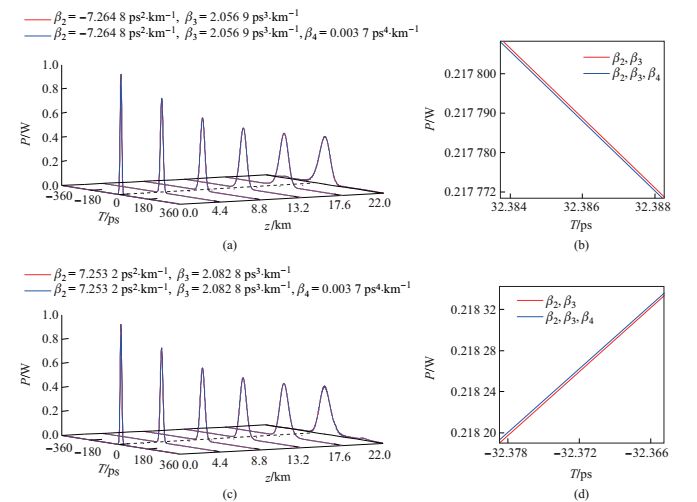
图 6中红色为
|
图 6 (a)、(c)相应于表 3中两种情况的高斯脉冲传输图, 其中红线没有考虑四阶色散; (b)、(d)脉冲传输到21 km时相应的半高带宽处的局部放大图
Fig.6 (a), (c) Pulse propagation for two cases in Table 3 and red line is for the case without |
据前分析, 超常介质中二阶、三阶色散都是较为严重的问题.即便是能够通过选取归一化频率使得
| $\beta _{21} L_1 +\beta _{22} L_2 =0, \quad {\beta _{31}L_1 +\beta _{32} L_2 =0},$ | (8) |
其中,
|
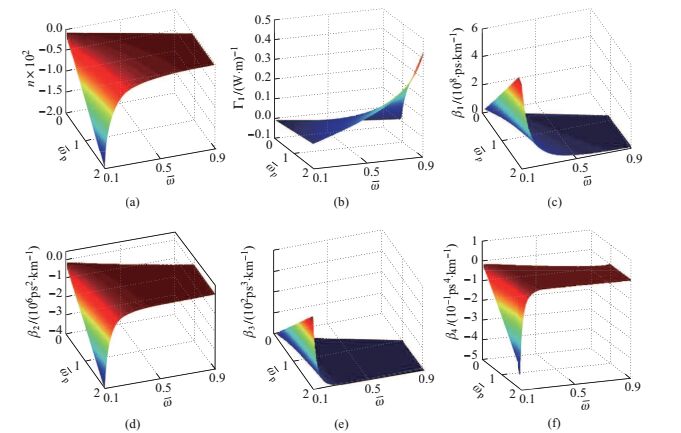
图 7 折射率n、三阶非线性系数和一阶、二阶、三阶、四阶色散系数分别随归一化频率 |
在图 7(d)和图 7(f)中
|
表 4 两组 |
将表 4中两种超常材料M1和M2交叉周期性排布, 可以得到一个平均GVD很小甚至可以忽略的新型复合超常材料.取M1和M2的长度
|
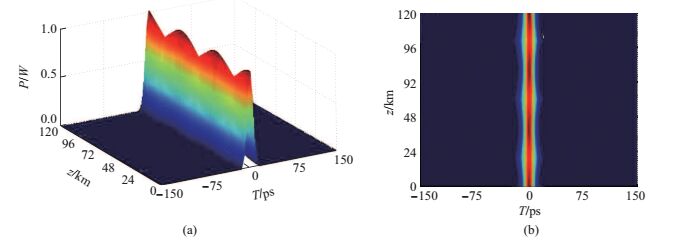
图 8 (a)高斯脉冲在复合超常材料M1+M2中色散补偿后传输120 km的脉冲波形变化图; (b)为(a)的俯视图, 即高斯脉冲能量扩散图 Fig.8 (a) Waveform variation of Gaussian pulse' 120 km propagation in compound metamaterials M1+M2; (b) Top view of (a) |
从图 8(a)可以看出, 脉冲在M1中传输时, 脉冲的宽度随着传输距离增加而展宽, 脉冲的幅值则因为脉冲的展宽而下降.当传输距离为
本文研究了超常材料中高阶色散与归一化频率的关系, 发现超常材料的二阶色散和高阶色散与一些常规介质相比非常之大, 对脉冲的传输有更为严重的影响.虽然我们找到了
从仿真中还可看出,
| [1] | SIMTH D R, KROLL N. Negative refractive index in left-handed materials[J]. Phys Rev Lett, 2000, 85(14): 2933-2936. DOI:10.1103/PhysRevLett.85.2933 |
| [2] | VESELAGO V G. The electrodynamics of substances with simultaneously negative values of μ and "[J]. Sov Phys Usp, 1968, 10(4): 509-514. DOI:10.1070/PU1968v010n04ABEH003699 |
| [3] | BERMAN P R. Goos-Hächen shift in negatively refractive media[J]. Phys Rev E, 2002, 66(6): 067603 DOI:10.1103/PhysRevE.66.067603 |
| [4] | ZHAROV A A, SHADRIVOV I V, KIVSHAR Y S. Nonlinear properties of left-handed metamaterials[J]. Phys Rev Lett, 2005, 30(24): 3356-3358. |
| [5] | LAZARIDES N, TSIRONIS G P. Coupled nonlinear Schröinger field equations for electromagnetic wave propagation in nonlinear left-handed materials[J]. Phys Rev E, 2005, 71: 036614 DOI:10.1103/PhysRevE.71.036614 |
| [6] | ZIOLKOWSKI R W. Superluminal transmission of information through an electromagnetic metamaterial[J]. Phys Rev E, 2001, 63: 046604 DOI:10.1103/PhysRevE.63.046604 |
| [7] | ZIOLKOWSKI R W. Pulsed and CW Gaussian beam interactions with double negative metamaterial slabs[J]. Opt Exp, 2003, 11: 662-681. DOI:10.1364/OE.11.000662 |
| [8] | WEN S C, XIANG Y J, DAI X Y, et al. Theoretical models for ultrashort electromagnetic pulse propagation in nonlinear metamaterials[J]. Phys Rev A, 2007, 75: 033815 DOI:10.1103/PhysRevA.75.033815 |
| [9] | JOSEPH A, PORSEZIAN K. Stability criterion for Gaussian pulse propagation through negative index materials[J]. Phys Rev A, 2010, 81: 023805 DOI:10.1103/PhysRevA.81.023805 |
| [10] | SARMA A K. Solitary wave solution to the generalized nonlinear Schrödinger equation for dispersive permittivity and permeability[J]. Eur Phys J D, 2011, 62: 421 DOI:10.1140/epjd/e2011-10288-0 |
| [11] | SARMA A K. Modulational instability of coupled nonlinear field equations for pulse propagation in a negative index material embedded into a Kerr medium[J]. J Opt Soc Am B(JOSA–B), 2011, 28(4): 944 DOI:10.1364/JOSAB.28.000944 |
| [12] | SAHA M, SARMA A K. Modulation instability in nonlinear metamaterials induced by cubic-quantic nonlinearities and higher order dispersive effects[J]. Opt Commn, 2012, 291: 321-325. DOI:10.1016/j.optcom.2012.11.011 |
| [13] | SCALORA M, SYRCHIN M S, AKOZBEK N, et al. Generalized non-linear Schrödinger equation for dispersive susceptibility and permeability: Application to negative index materials[J]. Phys Rev Lett, 2005, 95(1): 013902 DOI:10.1103/PhysRevLett.95.013902 |
| [14] | YANG R, ZHANG Y. Exact combined solitary wave solutions in nonlinear metamaterials[J]. J Opt Soc Am B(JOSA–B), 2011, 28: 123-127. DOI:10.1364/JOSAB.28.000123 |
| [15] | THORLABS. Inc: Dispersion-compensating prism pairs for ultrafast lasers[EB/OL]. [2016-04-10]. https://www.thorlabschina.cn/images/TabImages/AFSprismsGVDG2-480.gif.< |
| [16] | THORLABS.Inc: Dispersion-compensating prism pairs for ultrafast lasers[EB/OL]. [2016-04-10]. https://www.thorlabschina.cn/images/TabImages/AFSprismsTODG2-800.gif. |




