由于非线性偏微分方程能够描述物理、生物、化学和医学等领域中的复杂现象, 而且越来越多的数学、物理和工程问题要转化为非线性偏微分方程的求解问题.因此, 研究偏微分方程有重要的意义.而非线性偏微分方程的精确解可以更好地解释某些物理现象.经过多年研究, 人们已经提出许多行之有效的方法, 比如经典李群方法[1-3], Hirota双线性方法[4-5], 修正的CK直接约化方法[6-7], 齐次平衡方法[8-10]等.其中李群方法是研究微分方程的有力工具之一, 寻找方程的李点对称, 由已知解生成新解, 从而建立新解和旧解之间的联系.而且这种方法不仅适用于常系数方程和方程组, 而且适用于变系数方程.考虑以下变系数四阶偏微分方程
| $ \begin{equation} u_{t}+\alpha(t)u^{p}u_{x}+\beta u_{xxxx}=0, \end{equation} $ | (1) |
其中
本文由以下几部分组成:第1节求出方程(1)的李点对称; 第2节, 以
设方程(1)的单参数向量场为
| $ \begin{equation} V=\xi(x, t, u)\frac{\partial}{\partial x}+\tau(x, t, u)\frac{\partial}{\partial t}+\phi(x, t, u)\frac{\partial}{\partial u}, \end{equation} $ | (2) |
其中
| $ \begin{equation} \mathit{\rm{pr}}^{(4)}V(\Delta)|_{\Delta=0}=0, \end{equation} $ | (3) |
其中
| $ \begin{equation} \phi^{t}+\alpha'(t)\tau u^{p}u_{x}+p\alpha(t)u^{p-1}u_{x}\phi+ \alpha(t)u^{p}\phi^{x}+\beta\phi^{xxxx}=0, \end{equation} $ | (4) |
其中系数函数为
| $ \begin{align} u^{2}_{xx}: \phi_{uu}&=0, \nonumber\\ u_{xxxx}:\tau_{x}=0,&\Longrightarrow \tau=\tau(t), \nonumber\\ \cdots& \nonumber\\ u^{p}u_{x}: p\alpha(t)C_{4}+[4t\alpha'(t)+& 3\alpha(t)]C_{1}+\alpha'(t)C_{2}=0. \end{align} $ | (5) |
解以上方程组得
| $ \begin{equation} \xi=C_{1}x+C_{3}, \tau=4C_{1}t+C_{2}, \phi=C_{4}u, \end{equation} $ | (6) |
其中
下面根据
情况(ⅰ)
当
| $ \xi=C_{1}x+C_{3}, \tau=4C_{1}t+C_{2}, \phi=-\frac{3}{p}u, $ |
则生成元为
| $ \begin{equation} V_{1}=\frac{\partial}{\partial t}+x\frac{\partial}{\partial x}-\frac{3u}{p}\frac{\partial}{\partial u}, V_{2}=\frac{\partial}{\partial t}, \quad V_{3}=\frac{\partial}{\partial x}. \end{equation} $ | (7) |
情况(ⅱ)
(1) 当
| $ \xi=C_{1}x+C_{3}, \tau=4C_{1}t, \phi=0, $ |
则生成元为
| $ \begin{equation} V_{1}=4t\frac{\partial}{\partial t}+x\frac{\partial}{\partial x}, V_{2}=\frac{\partial}{\partial x}. \end{equation} $ | (8) |
(2) 当
(a)
| $ \xi=C_{3}, \tau=C_{2}, \phi=-kC_{2}u, $ |
则生成元为
| $ \begin{equation} V_{1}=\frac{\partial}{\partial t}-ku\frac{\partial}{\partial u}, V_{2}=\frac{\partial}{\partial x}. \end{equation} $ | (9) |
(b)
| $ \xi=C_{1}x+C_{3}, \tau=4C_{1}t-kC_{1}, \phi=0, $ |
则生成元为
| $ \begin{equation} V_{1}=(4t-k)\frac{\partial}{\partial t}+x\frac{\partial}{\partial x}, V_{2}=\frac{\partial}{\partial x}. \end{equation} $ | (10) |
(c)
| $ \xi=C_{1}x+C_{3}, \tau=4C_{1}, \phi=-kC_{1}u, $ |
则生成元为
| $ \begin{equation} V_{1}=4t\frac{\partial}{\partial t}+x\frac{\partial}{\partial x}-k\frac{\partial}{\partial u}, V_{2}=\frac{\partial}{\partial x}. \end{equation} $ | (11) |
(d)
前文中我们已经求出了方程(1)的李点对称, 下面以
当
| $ \begin{equation} u_{t}+ku^{3}u_{x}+\beta u_{xxxx}=0. \end{equation} $ | (12) |
(a) 对于向量场
| $ \begin{equation} -\dfrac{1}{4}\xi f'-\frac{1}{4}f+kf^{3}f'+\beta f^{(4)}=0, \end{equation} $ | (13) |
其中
(b) 对于向量场
| $ \begin{equation} -cf'+kf^{3}f'+\beta f^{(4)}=0, \end{equation} $ | (14) |
其中
(1) 当
| $ \begin{equation} u_{t}+kt^{-\frac{3}{4}}u^{3}u_{x}+\beta u_{xxxx}=0. \end{equation} $ | (15) |
对于向量场
| $ \begin{equation} -\frac{1}{4}\xi f'+kf^{3}f+\beta f^{(4)}=0, \end{equation} $ | (16) |
其中
(2) 当
(a)
| $ \begin{equation} u_{t}+l{\rm{e}}^{3kt}u^{3}u_{x}+\beta u_{xxxx}=0. \end{equation} $ | (17) |
对于向量场
| $ \begin{equation} kf+lf^{3}f'+\beta f^{(4)}=0, \end{equation} $ | (18) |
其中
(b)
| $ \begin{equation} u_{t}+l(4t-k)^{-\frac{3}{4}}u^{3}u_{x}+\beta u_{xxxx}=0. \end{equation} $ | (19) |
对于向量场
| $ \begin{equation} -\frac{1}{4}\xi f'+lf^{3}f+\beta f^{(4)}=0, \end{equation} $ | (20) |
其中
(c)
| $ \begin{equation} u_{t}+lt^{\frac{3k-3}{4}}u^{3}u_{x}+\beta u_{xxxx}=0. \end{equation} $ | (21) |
对于向量场
| $ \begin{equation} -\frac{1}{4}\xi f'-\frac{k}{4}f+lf^{3}f+\beta f^{(4)}=0, \end{equation} $ | (22) |
其中
(d)
前文中, 我们通过讨论
对方程(13)积分一次, 得
| $ \begin{equation} \xi f-kf^{4}-4\beta f'''=A_{0}, \end{equation} $ | (23) |
其中
| $ \begin{equation} f(\xi)=\sum\limits_{n=0}^{m}a_{m}(\xi)\varphi^{m}(a_{1}(\xi)\neq0), \end{equation} $ | (24) |
由齐次平衡原理得
| $ \begin{equation} f(\xi)=a_{1}(\xi)\varphi+a_{0}(\xi), \end{equation} $ | (25) |
其中
| $ \begin{equation} \varphi'(\xi)=A+B\varphi(\xi)+C\varphi^{2}(\xi), \end{equation} $ | (26) |
其中
把式(25)、(26)代入方程(23)中, 比较
| $ a_{1}=-\sqrt[3]{\frac{24\beta}{k}}C(\xi), a_{0}=-\sqrt[3]{\frac{24\beta}{k}}\left(\frac{B(\xi)}{2}+\frac{5C'(\xi)}{12C(\xi)}\right), A_{0}=0. $ |
当
| $ f_{1}(\xi)=-\sqrt[3]{\frac{24\beta}{k}}\left[\frac{\Delta_{1}}{2} \left(\frac{C_{1}\sinh\frac{1}{2}\Delta_{1}\xi+C_{2}\cosh\frac{1}{2}\Delta_{1}\xi}{C_{1}\cosh\frac{1}{2}\Delta_{1}\xi+C_{2}\sinh\frac{1}{2}\Delta_{1}\xi}\right)+\frac{C'}{6C}+\frac{B}{2}\right], $ |
故方程(12)的精确解为
| $ u_{1}(x, t)=-\sqrt[3]{\frac{24\beta}{k}}\left[\frac{\Delta_{1}}{2} \left(\frac{C_{1}\sinh\frac{1}{2}\Delta_{1}xt^{-\frac{1}{4}}+C_{2}\cosh\frac{1}{2}\Delta_{1}xt^{-\frac{1}{4}}}{C_{1}\cosh\frac{1}{2}\Delta_{1}xt^{-\frac{1}{4}}+C_{2}\sinh\frac{1}{2}\Delta_{1}xt^{-\frac{1}{4}}}\right) +\frac{C'}{6C}+\frac{B}{2}\right]t^{-\frac{1}{4}}. $ |
其中
当
| $ f_{2}(\xi)=-\sqrt[3]{\frac{24\beta}{k}}\left[\frac{\Delta_{2}}{2} \left(-\frac{C_{1}\sin\frac{1}{2}\Delta_{2}\xi+C_{2}\cos\frac{1}{2}\Delta_{2}\xi}{C_{1}\cos\frac{1}{2}\Delta_{2}\xi+C_{2}\sin\frac{1}{2}\Delta_{2}\xi}\right)+\frac{C'}{6C}+\frac{B}{2}\right], $ |
故方程(12)的精确解为
| $ u_{2}(x, t)=-\sqrt[3]{\frac{24\beta}{k}}\left[\frac{\Delta_{2}}{2} \left(-\frac{C_{1}\sin\frac{1}{2}\Delta_{2}xt^{-\frac{1}{4}}+C_{2}\cos\frac{1}{2}\Delta_{2}xt^{-\frac{1}{4}}}{C_{1}\cos\frac{1}{2}\Delta_{2}xt^{-\frac{1}{4}}+C_{2}\sin\frac{1}{2}\Delta_{2}xt^{-\frac{1}{4}}}\right) +\frac{C'}{6C}+\frac{B}{2}\right]t^{-\frac{1}{4}}. $ |
其中
当
| $ f_{3}(\xi)=-\sqrt[3]{\frac{24\beta}{k}}\left(\frac{C_{2}}{C_{1}+C_{2}\xi}+\frac{C'}{6C}+\frac{B}{2}\right), $ |
故方程(12)的精确解为
| $ u_{3}(x, t)=-\sqrt[3]{\frac{24\beta}{k}}\left(\frac{C_{2}}{C_{1}+C_{2}xt^{-\frac{1}{4}}}+\frac{C'}{6C}+\frac{B}{2}\right)t^{-\frac{1}{4}}, $ |
其中
对方程(14)积分一次得
| $ \begin{equation} cf-\frac{k}{4}f^{4}-\beta f'''=B_{0}, \end{equation} $ | (27) |
其中
| $ \begin{equation} f(\xi)=\sum\limits_{n=0}^{m}k_{m}\varphi^{m}, \end{equation} $ | (28) |
由齐次平衡原理得
| $ \begin{equation} f(\xi)=k_{1}\varphi+k_{0}, \end{equation} $ | (29) |
其中
| $ \begin{equation} \varphi'=A+B\varphi+C\varphi^{2}, \end{equation} $ | (30) |
其中
| $ k_{1}=\sqrt[3]{\frac{24\beta}{k}}C, k_{0}=\frac{B}{2}\sqrt[3]{\frac{24\beta}{k}}C, B_{0}=\left(\frac{3B^{4}C^{4}\beta^{2}}{2k}+\frac{A^{2}C^{2}k}{2}+\frac{AkCB^{2}}{4}-\frac{BC}{2}\right)\sqrt[3]{\frac{24\beta}{k}}. $ |
我们给出
当
| $ \varphi_{1}=\coth\xi\pm \mathit{\rm{csch}}\xi, \varphi_{2}=\tanh\xi\pm \mathit{{\rm{sech}}}\xi, \varphi_{3}=\frac{\tanh \xi}{1\pm \mathit{{\rm{sech}}}\xi}, \varphi_{4}=\frac{\coth \xi}{1\pm \mathit{\rm{csch}}\xi}, $ |
故方程(27)的解为
| $ \begin{align*} &f_{4}(\xi)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}(\coth\xi\pm \mathit{\rm{csch}}\xi), \quad f_{5}(\xi)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}(\tanh\xi\pm \mathit{{\rm{sech}}}\xi), \\[2mm] &f_{6}(\xi)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}\Big(\frac{\tanh \xi}{1\pm \mathit{{\rm{sech}}}\xi}\Big), \quad f_{7}(\xi)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}\Big(\frac{\coth \xi}{1\pm \mathit{\rm{csch}}\xi}\Big). \end{align*} $ |
对于方程(14)的解
| $ u_{4}(x, t)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}[\coth(x-ct)\pm \mathit{\rm{csch}}(x-ct)], $ |
借助Maple软件,
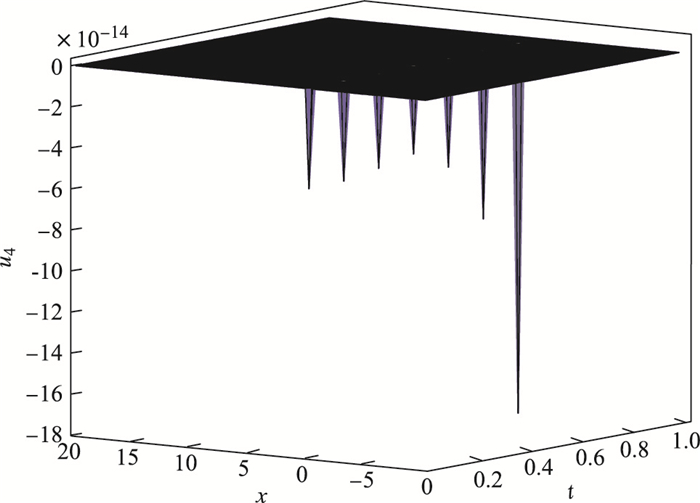
|
图 1 当 |
对于方程(14)的解
| $ u_{5}(x, t)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}\left[\tanh(x-ct)\pm \mathit{{\rm{sech}}}(x-ct)\right], $ |
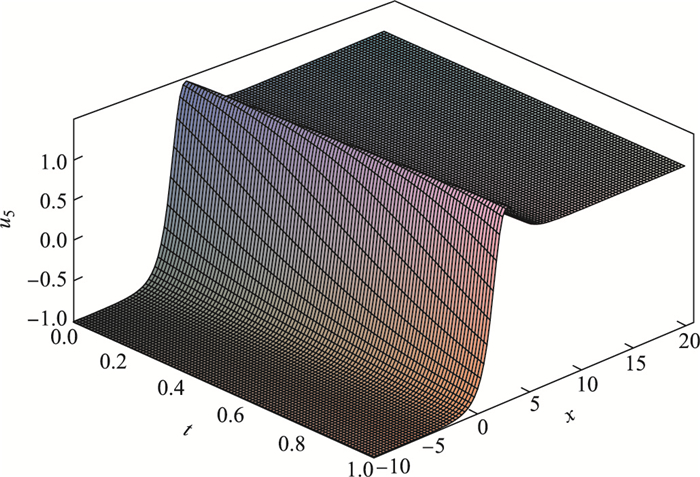
|
图 2 当 |
对于方程(14)的解
| $ u_{6}(x, t)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}\left[\frac{\tanh (x-ct)}{1\pm \mathit{{\rm{sech}}}(x-ct)}\right], $ |
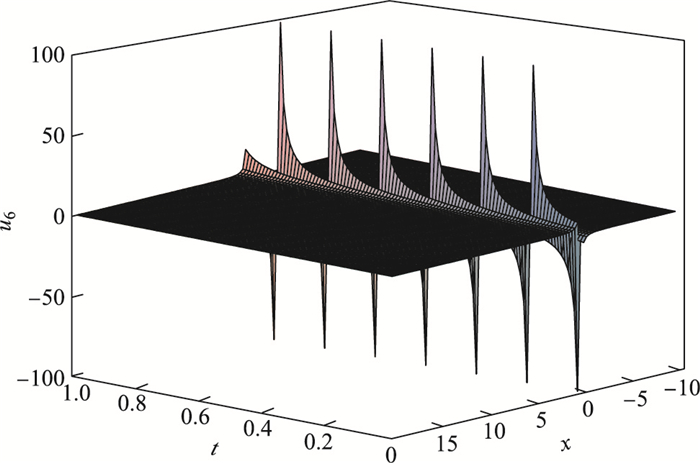
|
图 3 当 |
对于方程(14)的解
| $ u_{7}(x, t)=\frac{1}{2}\sqrt[3]{\frac{24\beta}{k}}\left[\frac{\coth (x-ct)}{1\pm \mathit{\rm{csch}}(x-ct)}\right]. $ |
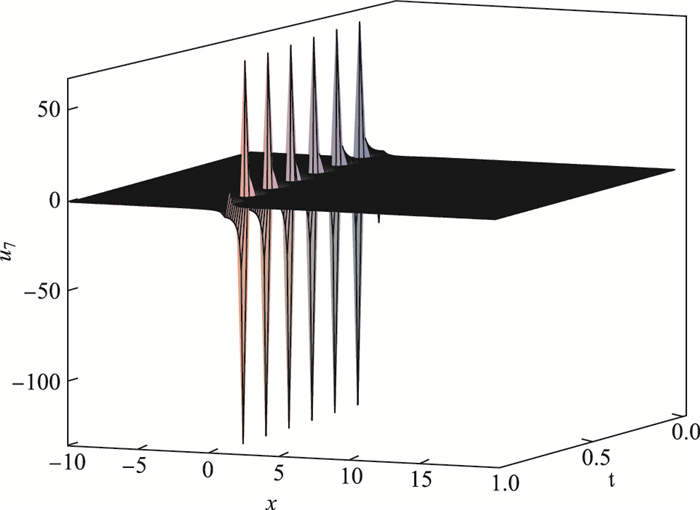
|
图 4 当 |
假设方程(16)有如下形式的幂级数展开解
| $ \begin{equation} f(\xi)=\sum\limits_{n=0}^{\infty}C_{n}\varphi^{n}, \end{equation} $ | (31) |
把式(31)代入方程(16)中, 得
| $ \begin{array}{l} l\sum\limits_{n = 1}^\infty {\left( {\sum\limits_{k = 0}^n {\sum\limits_{j = 0}^k {\sum\limits_{m = 0}^j {(n + 1 - k)} } } {C_m}{C_{j - m}}{C_{k - j}}{C_{n - k}}} \right)} {\xi ^n} - \frac{1}{4}\sum\limits_{n = 1}^\infty n {C_n}{\xi ^n} + lC_0^3{C_1}\\ \;\;\;\;\;\;\;\;\;\;\;\; + 24\beta {C_4} + \beta \sum\limits_{n = 1}^\infty {(n + 1)} (n + 2)(n + 3)(n + 4){C_{n + 4}}{\xi ^n} = 0, \end{array} $ | (32) |
比较式(32)中的系数, 可得:当
当
| $ \begin{equation} C_{n+4}=\frac{\frac{1}{4}nC_{n}-l\sum\limits_{k=0}^{n}\sum\limits_{j=0}^{k}\sum\limits_{m=0}^{j}C_{m}C_{j-m}C_{k-j}C_{n+1-k}}{\beta(n+1)(n+2)(n+3)(n+4)}, \end{equation} $ | (33) |
其中
| $ C_{5}=\frac{C_{1}-8lC^{3}_{0}C_{2}+4lC^{2}_{0}C^{2}_{1}+8lC_{0}C^{3}C_{1}+4lC^{2}_{0}C_{1}C_{2}}{480\beta}. $ |
故方程(16)的解为
| $ f_{8}(\xi)=C_{0}+C_{1}\xi+C_{2}\xi^{2}+C_{3}\xi^{3}+\sum\limits_{n=0}^{\infty}C_{n+4}\xi^{n+4}, $ |
因此得原方程(15)的精确幂级数展开解为
| $ u_{8}(x, t)=C_{0}+C_{1}(xt^{-\frac{1}{4}}) C_{2}(xt^{-\frac{1}{4}})^{2}+C_{3}(xt^{-\frac{1}{4}})^{3}+ \sum\limits_{n=0}^{\infty}C_{n+4}(xt^{-\frac{1}{4}})^{n+4}, $ |
其中
假设方程(18)有如下形式的
| $ \begin{equation} f(\xi)=\sum\limits_{n=0}^{m}\alpha_{m}\left(\frac{G'}{G}\right)^{m}, \end{equation} $ | (34) |
其中
| $ \begin{equation} G''+\lambda G'+\mu G=0. \end{equation} $ | (35) |
由式(34)和(35)得
| $ f^{(4)}=m(m+1)(m+2)(m+3)(m+4)\alpha_{m}\left(\frac{G'}{G}\right)^{m+4}+\cdots, $ | (36) |
| $ f^3=\alpha^{3}_{m}\left(\frac{G'}{G}\right)^{3m}+\cdots, $ | (37) |
| $ f'=-m\alpha_{m}\left(\frac{G'}{G}\right)^{m+1}+\cdots. $ | (38) |
把式(34)-(38)代入方程(18), 平衡最高阶导数项
| $ \begin{equation} f(\xi)=\alpha_{1}\left(\frac{G'}{G}\right)+\alpha_{0}, \end{equation} $ | (39) |
把式(35)-(39)代入方程(18)中, 且令式中
| $ \alpha_{1}=\frac{2\sqrt[3]{3\beta l^{2}}}{l}, \quad \alpha_{0}=\frac{\lambda\sqrt[3]{3\beta l^{2}}}{l}. $ |
当
| $ f_{9}(\xi)=\frac{\sqrt[3]{3\beta l^{2}}\sqrt{\lambda^{2}-4\mu}}{l} \left(\frac{C_{1}\sinh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}\xi+C_{2}\cosh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}\xi}{C_{1}\cosh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}\xi+C_{2}\sinh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}\xi}\right), $ |
故方程(17)的精确解为
| $ u_{9}(x, t)=\frac{\sqrt[3]{3\beta l^{2}}\sqrt{\lambda^{2}-4\mu}}{l} \left(\frac{C_{1}\sinh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}x+C_{2}\cosh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}x}{C_{1}\cosh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}x+C_{2}\sinh\frac{1}{2}\sqrt{\lambda^{2}-4\mu}x}\right){\rm{e}}^{-kt}, $ |
当
| $ f_{10}(\xi)=\frac{\sqrt[3]{3\beta l^{2}}\sqrt{4\mu-\lambda^{2}}}{l} \left(\frac{-C_{1}\sin\frac{1}{2}\sqrt{4\mu-\lambda^{2}}\xi+C_{2}\cos\frac{1}{2}\sqrt{4\mu-\lambda^{2}}\xi}{C_{1}\cos\frac{1}{2}\sqrt{4\mu-\lambda^{2}}\xi+C_{2}\sin\frac{1}{2}\sqrt{4\mu-\lambda^{2}}\xi}\right), $ |
故方程(17)的精确解为
| $ u_{10}(x, t)=\frac{\sqrt[3]{3\beta l^{2}}\sqrt{4\mu-\lambda^{2}}}{l} \left(\frac{-C_{1}\sin\frac{1}{2}\sqrt{4\mu-\lambda^{2}}x+C_{2}\cos\frac{1}{2}\sqrt{4\mu-\lambda^{2}}x}{C_{1}\cos\frac{1}{2}\sqrt{4\mu-\lambda^{2}}x+C_{2}\sin\frac{1}{2}\sqrt{4\mu-\lambda^{2}}x}\right){\rm{e}}^{-kt}, $ |
当
| $ f_{11}(\xi)=\frac{2\sqrt[3]{3\beta l^{2}}C_{2}}{l(C_{1}+C_{2}\xi)}, $ |
故原方程(17)的精确解为
| $ u_{11}(x, t)=\frac{2\sqrt[3]{3\beta l^{2}}C_{2}{\rm{e}}^{-kt}}{l(C_{1}+C_{2}x)}, $ |
其中
在这一部分, 我们将给出方程(1)的伴随方程和守恒律.
方程(1)的伴随方程为
| $ \begin{equation} F^{*}=v_{t}+\alpha(t)u^{p}v_{x}-\beta v_{xxxx}=0, \end{equation} $ | (40) |
设
| $ \begin{equation} F^{*}\mid_{v=\psi}=\lambda(x, t, u, \cdots)F, \end{equation} $ | (41) |
其中
| $ \psi_{t}+\beta \psi_{xxxx}+(\psi_{u}+\lambda)u_{t}+\alpha(t)u^{p}\psi_{x}-4\beta \psi_{uxxx}u_{x}-6\beta \psi_{uuxx}u^{2}_{x} -6\beta \psi_{uxx}u_{xx} $ |
| $ -4\beta \psi_{uuux}u^{3}_{x}+12\beta \psi_{uux}u_{x}u_{xx}-\beta \psi_{uuuu}u^{4}_{x}-6\beta \psi_{uuu}u^{2}_{x}u_{xx} -4\beta \psi_{ux}u_{xxx} $ |
| $ -4\beta \psi_{uu}u_{x}u_{xxx}+\beta(\lambda- \psi_{u})u_{xxxx}-3\beta \psi_{uu}u^{2}_{xx}+\alpha(t)\lambda u^{p}u_{x}=0. $ |
比较
| $ L=v(u_{t}+\alpha(t)u^{p}u_{x}+\beta u_{xxxx}), $ |
利用Ibragimov给出的结论, 守恒向量为
| $ \begin{align} C^{i}=&\xi^{i}L+W^{\alpha}\left[\frac{\partial L}{\partial u^{\alpha}_{i}}-D_{i}D_{k}D_{m}\left(\frac{\partial L}{\partial u^{\alpha}_{ijkm}}\right)\right]+D_{i}(W^{\alpha}) \left[D_{k}D_{m}\left(\frac{\partial L}{\partial u^{\alpha}_{ijkm}}\right)\right] \nonumber\\[2mm] &+D_{j}D_{k}(W^{\alpha})\left[-D_{m}\left(\frac{\partial L}{\partial u^{\alpha}_{ijkm}}\right)\right]+D_{j}D_{k}D_{m}(W^{\alpha})\frac{\partial L}{\partial u^{\alpha}_{ijkm}}, \end{align} $ | (42) |
其中
根据Ibragimov给出的结论, 给出向量场的通式
| $ V=\xi^{1}(x, t, u)\frac{\partial}{\partial t}+\xi^{2}(x, t, u)\frac{\partial}{\partial x}+\phi \frac{\partial}{\partial u}, $ |
那么方程(1)的守恒律由下式决定
| $ D_{t}(C^{1})+D_{x}(C^{2})=0, $ |
向量场
| $ C^{1}= \xi ^{1}L+W\left(\frac{\partial L}{\partial u_{t}}\right), $ | (43) |
| $ \begin{align} C^{2}=&\xi ^{2}L+W\left[\frac{\partial L}{\partial u_{x}}-D_{xxx}\left(\frac{\partial L}{\partial u_{xxxx}}\right)\right]+D_{x}(W)\left[D_{xx}\left(\frac{\partial L}{\partial u_{xxxx}}\right)\right] \nonumber\\[2mm] &+D_{xx}\left[-D_{x}\left(\frac{\partial L}{\partial u_{xxxx}}\right)\right] +D_{xxx}\frac{\partial L}{\partial u_{xxxx}}. \end{align} $ | (44) |
以下面情况(ⅰ)和情况(ⅱ)为例, 可分别求出显式守恒律.
情况(ⅰ)
考虑方程(12), 对于向量场
| $ V_{1}=4t\frac{\partial}{\partial t}+x\frac{\partial}{\partial x}-u\frac{\partial}{\partial u}, $ |
有
| $ \begin{array}{l} {C^1} = {\xi ^1}L + W\left( {\frac{{\partial L}}{{\partial {u_t}}}} \right)\\ \;\;\;\; = \rho (4kt{u^3}{u_x} + 4\beta t{u_{xxxx}} - x{u_x}), \end{array} $ | (45) |
| $ \begin{align} C^{2}=&\xi ^{2}L+W\left[\frac{\partial L}{\partial u_{x}}-D_{xxx}\left(\frac{\partial L}{\partial u_{xxxx}}\right)\right]+D_{x}(W)\left[D_{xx}\left(\frac{\partial L}{\partial u_{xxxx}}\right)\right] \nonumber\\[1mm] =&\rho (xu_{t}-ku^{4}-4ktu^{3}u_{t}-4\beta u_{xxx}-4\beta tu_{xxxt}).\quad\quad\quad\quad \quad\quad \end{align} $ | (46) |
情况(ⅱ)
考虑方程(17), 对于向量场
| $ V_{1}=\frac{\partial}{\partial t}-ku\frac{\partial}{\partial u}, $ |
有
| $ \begin{align} C^{1}=&\xi ^{1}L+W\left(\frac{\partial L}{\partial u_{t}}\right) \nonumber\\[1mm] =&\rho (l{\rm{e}}^{3kt}u^{3}u_{x}+\beta u_{xxxx}-ku), \end{align} $ | (47) |
| $ \begin{align} C^{2}=&\xi ^{2}L+W\left[\frac{\partial L}{\partial u_{x}}-D_{xxx}\left(\frac{\partial L}{\partial u_{xxxx}}\right)\right]+D_{x}(W)\left[D_{xx}\left(\frac{\partial L}{\partial u_{xxxx}}\right)\right] \nonumber\\[1mm] =&-\rho (kl{\rm{e}}^{3kt}u^{4}+l{\rm{e}}^{3kt}u^{3}u_{t}+k\beta u_{xxx}+\beta u_{xxxt}). \end{align} $ | (48) |
以上守恒向量
本文运用李群分析研究了一类变系数四阶偏微分方程, 把复杂的偏微分方程约化成常微分方程, 通过求常微分方程的精确解, 得到原方程的精确解, 包括三角函数解, 幂级数展开解, 椭圆函数解等.进而可以建立新解和旧解之间的关系, 能更好地解释复杂的物理现象.李群是研究微分方程的有力工具之一, 无论是研究常系数偏微分方程还是变系数偏微分方程, 都具有广泛的应用.另外, 我们给出了四阶变系数方程的伴随方程和显式守恒律.
| [1] | 田畴. 李群及其在微分方程中的应用[M]. 北京: 科学出版社, 2001. |
| [2] | OLVER P. Applications of Lie Groups to Differential Equations[M]. New York: Springer, 1993. |
| [3] | BLUMAN G, ANCO S. Symmetry and Integration Methods for Differential Equations[M]. New York: SpringerVerlag, 2002. |
| [4] | HIROTA R, SATSUMA J. A variety of nonlinear network equations generated form the Bäcklund transformation for the Tota lattice[J]. Suppl Prog Theor Phys, 1976, 59: 64-100. DOI:10.1143/PTPS.59.64 |
| [5] | LIU H Z, LI J B, CHEN F J. Exact periodic wave solutions for the mKdV equations[J]. Nonlinear Anal, 2009, 70: 2376-2381. DOI:10.1016/j.na.2008.03.019 |
| [6] | WANG G W, XU T Z, LIU X Q. New explicit solutions of the fifth-order KdV equation with variable cóefficients[J]. Bull Malays Math Sci Soc, 2014, 37(3): 769-778. |
| [7] | 胡晓瑞. 非线性系统的对称性与可积性[D]. 上海: 华东师范大学, 2012, 43-77. http://cdmd.cnki.com.cn/Article/CDMD-10269-1012435961.htm |
| [8] | 刘大勇, 夏铁成. 齐次平衡法寻找Caudrey-Dodd-Gibbon-Kaeada方程的多孤子解[J]. 应用数学和计算数学学报, 2011, 25(2): 205-212. |
| [9] | 刘丽环, 常晶, 冯雪. 求非线性发展方程行波解的(G'/G)展开法[J]. 吉林大学学报(理学版), 2013, 51(2): 183-186. |
| [10] | 张辉群. 齐次平衡方法的扩展及应用[J]. 数学物理学报, 2001, 21A(3): 321-325. |
| [11] | YAO Q L. Existence, multiplicity and infinite solvability of positive solutions to a nonlinear fourth-order periodic boundary value problem[J]. Nonlinear Analysis, 2005, 63: 237-246. DOI:10.1016/j.na.2005.05.009 |
| [12] | WANG M L, LI X Z, ZHANG J L. The (G'/G) -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J]. Phys Lett A, 2008, 372: 417-423. DOI:10.1016/j.physleta.2007.07.051 |
| [13] | 赵烨, 徐茜. 一类耦合Benjamin-Bona-Mahony型方程组的新精确解[J]. 纯粹数学与应用数学, 2015, 31: 12-17. DOI:10.3969/j.issn.1008-5513.2015.01.002 |
| [14] | LI K H, LIU H Z. Lie symmetry analysis and exact solutions for nonlinear LC circuit equation[J]. Chinese Journal of Quantum Electronics, 2016, 33: 279-286. |
| [15] | 杨春艳, 李小青. 一类四阶偏微分方程的对称分析及级数解[J]. 纯粹数学与应用数学, 2016, 32: 432-440. DOI:10.3969/j.issn.1008-5513.2016.04.011 |
| [16] | 徐兰兰, 陈怀堂. 变系数(2+1)维Nizhnik-Novikov-Vesselov的三孤子新解[J]. 物理学报, 2013, 62(9): 090204 |
| [17] | 魏帅帅, 李凯辉, 刘汉泽. 展开法在Riccati方程中的应用[J]. 河南科技大学学报, 2015, 36: 92-96. DOI:10.3969/j.issn.1672-6871.2015.02.022 |
| [18] | IBRAGIMOV N H. Integrating factors, adjoint equations and Lagrangians[J]. J Math Anal Appl, 2006, 38: 742-757. |
| [19] | IBRAGIMOV N H. A new conservation theorem[J]. J Math Anal Appl, 2007, 333: 311-328. DOI:10.1016/j.jmaa.2006.10.078 |
| [20] | IBRAGIMOV N H. Nonlinear self-adjointness and conservation laws[J]. J Phys A, 2011, 44: 432002(899) |
| [21] | ROSA R, GANDARIAS M L, BRUZON M S. Symmetries and conservation laws of a fifth-order KdV equation with time-dependent coefficients and linear damping[J]. Nonlinear Dyn, 2016, 84: 135-141. DOI:10.1007/s11071-015-2254-3 |
| [22] | YOMBA E. On exact solutions of the coupled Klein-Gordon-Schrödinger and the complex coupled KdV equations using mapping method[J]. Chaos, Solitons and Fractals, 2004, 21: 209-229. DOI:10.1016/j.chaos.2003.10.028 |




