复杂网络的理论及其应用自从Watts和Strogatz提出小世界网络以及Albert和Barab
本文延用L. Lacasa提出的可视图 (VG) 算法. VG算法将时间序列中的数据直接定义为复杂网络中的节点, 而节点间的连接关系由数据之间的线性可视关系决定.基于可视图方法, 随着时间序列数据的不断增加, 复杂网络的生成过程类似于Barabasi-Albert无尺度网络的动态生成过程, 而且复杂网络中的中心 (Hub) 节点对应于时间序列数值特别大的数据. VG算法能够将任意的时间序列转化为网络, 且为全连通网络, 不依赖于阈值的选取, 如周期时间序列能够转化成正则图、随机时间序列能够转化成随机图、分形时间序列能够转化成无标度网络.该方法已经在很多不同的领域内得到了很好的应用, 比如太阳黑子方面[9-10]、金融时间序列和飓风气候数据[11-15].最近, 又提出了水平可视图 (HVG) 算法[16], 同样得到了非常广泛的应用[17-18].
VG算法可将某些分形时间序列转化为无标度网络 (例如布朗运动序列), 即网络的度分布符合幂律分布[6].从数值角度看, 计算网络的幂率指数不是一个简单的事情, 在文献[6]中也并没有证明幂律分布是最优的度分布; 另外, 针对更加一般的随机时间序列, 刻画幂率分布是否可行, 以及在HVG算法中是否同样适用, 目前尚不明了.进一步刻画网络度分布的拟合问题, 无疑有助于理解网络化方法分析时间序列的基本问题.
本文首先简单介绍VG算法和HVG算法; 其次, 介绍本文的研究对象, 即自回归随机过程 (自回归随机时间序列) 和分数布朗运动; 最后, 通过这两种可视化算法, 把这两类数据转换为可视图, 对比分析后发现, 自回归随机过程的网络度分布符合指数分布, 而分数布朗运动的网络度分布近似幂律分布.
1 可视图网络生成算法VG算法的定义是:当给定的一组时间序列中, 任意两点 (
| $ \begin{align*} y_c < y_a+(y_b-y_a)\dfrac{t_c-t_a}{t_b-t_a} \end{align*} $ |
时, 则认为这两点可视, 即在网络中存在连边.现有结果表明可视图保留了原始数据的很多性质, 比如周期时间序列得到规则图、随机时间序列转化为随机网络图、分形序列对应标度网络[6]等.
HVG算法的定义是:如果任意两点 (
| $ \begin{align*} y_a, y_b>y_c \end{align*} $ |
时, 则认为这两点可视, 即在网络中相连.
2 两种时间序列介绍 2.1 自回归随机过程模型自回归随机过程模型 (简称为自回归模型) 是利用前期若干时刻的随机变量的线性组合来描述以后某时刻随机变量的线性回归模型, 它是时间序列中的一种常见形式.考虑一个时间序列
布朗运动过程是一种正态分布的独立增量连续随机过程, 而分数布朗运动 (Fractional Brownian Motion, FBM) 的增量不再是独立的, 这是对经典布朗运动的推广, 同时也是理想的不规则扩散和分形随机行走的基础.分数布朗运动的赫斯特指数
度分布是复杂网络中一个重要的概念.如果遵循指数分布时, 即网络的度分布为
|
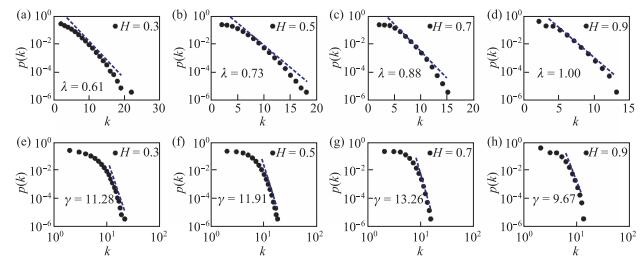
图 1 图 1(a)-图 1(d) 半对数坐标下的度累积分布的指数拟合, 虚线表示率参数 |
| 表 1 AR (1) 在VG算法下指数与幂率拟合比较 Tab.1 Comparison between exponential and power law scaling factors of VG graphs of AR (1) |
度分布斜线拟合的优劣运用相关系数平方
在VG算法下, 针对选取的不同参数
|
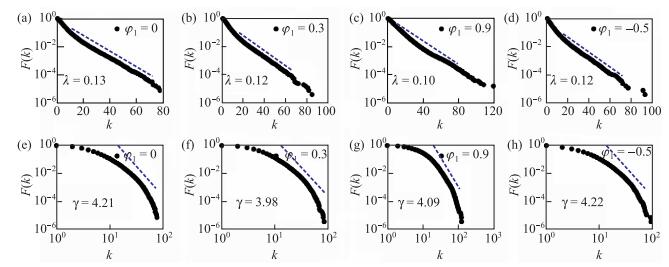
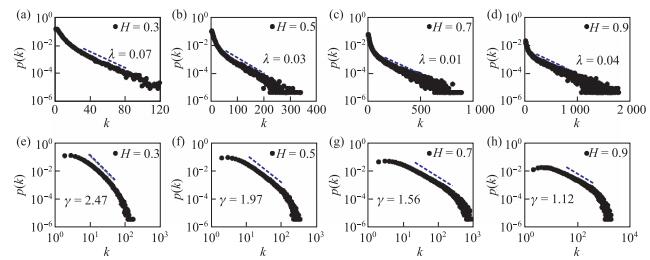
图 3 图 3(a)-图 3(b) 半对数坐标下的度分布的指数拟合, 虚线表示率参数 |
| 表 3 FBM在VG算法下指数与幂率拟合比较 Tab.3 Comparison between exponential and power law scaling factors VG graphs of FBM |
在HVG下, 可以得到相同的结论, 具体而言, 度分布和拟合结果如图 4和表 4所示.
4 结论本文将可视图方法应用在自回归随机过程和分数布朗运动中进行对比研究, 通过对指数拟合和幂律拟合的比较, 不论是在VG算法下, 还是在HVG算法下, 可得到以下结论.
(1) 对于自回归随机过程, 相较于幂律拟合, 指数拟合的残差平方和SSE更小, 相关系数平方
(2) 对于分数布朗运动时间序列, 相较于指数拟合, 幂律拟合的SSE更小,
传统时间序列分析的优劣性值得探讨, 尤其需要重视与回归网络、周期图等方法的比较研究; 在气候、金融和大脑等实际数据中的应用还有待于进一步研究.
| [1] | WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 6684(393): 440-442. |
| [2] | ALBERT R, BARABÁSI A L. Statistical mechanics of complex networks[J]. Review of Modern Physics, 2002, 74(1): 47-97. DOI:10.1103/RevModPhys.74.47 |
| [3] | 汪小帆. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006. |
| [4] | 何大韧. 复杂系统与复杂网络[M]. 北京: 高等教育出版社, 2009. |
| [5] | ZHANG J, SMALL M. Complex network from pseudoperiodic time series:topology versus dynamics[J]. Physical Review Letters, 2006, 96(23): 238701-238704. DOI:10.1103/PhysRevLett.96.238701 |
| [6] | LACASA L, LUQUE B, BALLESTEROS F, et al. From time series to complex networks:The visibility graph[J]. Proceedings of the National Academy of Sciences, 2008, 105(13): 4972-4975. DOI:10.1073/pnas.0709247105 |
| [7] | DONNER R V, ZOU Y, DONGES J F, et al. Recurrence networks-a novel paradigm for nonlinear time series analysis[J]. New Journal of Physics, 2010, 12(2): 129-132. |
| [8] | XU X K, ZHANG J, SMALL M. Superfamily phenomena and motifs of networks induced from time series[J]. Proceedings of the National Academy of Sciences, 2008, 105(50): 19601-19605. DOI:10.1073/pnas.0806082105 |
| [9] | ZOU Y, SMALL M, LIU Z H, et al. Complex network approach to characterize the statistical features of the sunspot series[J]. New Journal of Physics, 2014, 14(1): 1-8. |
| [10] | ZOU Y, DONNER R V, MARWAN N, et al. Long-term changes in the north-south asymmetry of solar activity:A nonlinear dynamics characterization using visibility graphs[J]. Nonlinear Processes in Geophysics, 2014, 21(1): 1113-1126. |
| [11] | YANG Y, YANG H. Complex network-based time series analysis[J]. Physica A, 2008, 387(s 5-6): 1381-1386. |
| [12] | LACASA L, TORAL R. Description of stochastic and chaotic series using visibility graphs[J]. Physical Review E, 2010, 82(3): 4881-4888. |
| [13] | GAO Z K, JIN N D. Flow-pattern identification and nonlinear dynamics of gas-liquid two-phase flow in complex networks[J]. Physical Review E, 2009, 79(6): 1019-1027. |
| [14] | YANG Y, WANG J, YANG H, et al. Visibility graph approach to exchange rate series[J]. Physica A, 2009, 388(20): 4431-4437. DOI:10.1016/j.physa.2009.07.016 |
| [15] | ELSNER J B, JAGGER T H, FOGARTY E A. Visibility network of United States hurricanes[J]. Geophysical Research Letters, 2009, 36(16): 554-570. |
| [16] | LUQUE B, LACASA L, BALLESTEROS F, et al. Horizontal visibility graphs:exact results for random time series[J]. Physical Review E, 2009, 80(2): 593-598. |
| [17] | GUTIN G, MANSOUR T, SEVERINI S. A characterization of horizontal visibility graphs and combinatorics on words[J]. Physica A, 2011, 390(12): 2421-2428. DOI:10.1016/j.physa.2011.02.031 |
| [18] | NUÑEN A, LACASA L, VALERO E, et al. Detecting series periodicit e y with horizontal visibility graphs[J]. International Journal of Bifurcation & Chaos, 2012, 22(7): 1250160(10pages) DOI:10.1142/S021812741250160X |