视觉是人们获得感知信息的主要方式, 视觉信息的主要来源是图像.在计算机网络技术和通信技术快速发展的同时, 在网络环境中存储和传输的数字图像的数量更是急剧增多.数字图像成为了网络中信息交流的主要信息载体.然而随着图像数量的增加, 暴露在网络中的信息也越来越多, 其中包括一些个人的隐私信息、企业乃至国家的涉密信息, 所以网络图像信息的安全问题日益受到重视.数字图像与一般的文本不同, 具有数据量大、相关性强以及冗余度高等特点, 这使得传统的密码学方法, 如DES(Data Encryption Standard)和AES(Advanced Encryption Standard)应用到图像加密场合的效果并不理想.在此背景下, 基于混沌的图像加密策略引起了广泛的关注[1-7].
混沌系统具有伪随机性、遍历性和初值敏感性等特点, 其在密码学的应用中具有明显的优势.同时, 混沌序列可以由混沌系统简单高效地生成, 故能满足加密需求.图像加密一般采用置乱--扩散机制:置乱过程是通过改变像素的位置来实现像素置乱; 扩散过程是对像素值的修改.早期所研究的图像加密算法都只是基于像素层面的置乱和扩散, 并不能打破图像固有的特性, 故而加密效果一般[4-7].因此, 近年来越来越多的研究着眼于基于比特位层面的加密, 并获得了理想的加密效果.混沌系统被广泛地运用到图像加密机制的各个阶段.汪彦等提出了改进的Lorenz混沌系统[8], 在混沌系统里加入了
本文基于Tent和Henon混沌系统, 提出了新的比特位平面的全局置乱算法, 对高位(在二进制表示中权重较大的位)和低位(在二进制表示中权重较小的位)采用不同的操作: ①对明文图像进行位平面分解, 并进行自适应的异或运算来修改高4位的位平面. ②位平面的置乱分为两个阶段:第一阶段, 分别对高4位和低4位组成的图像进行像素置乱; 第二阶段, 通过两两分组的方法形成4个平面, 进一步组成一幅新图像后再次进行像素的置乱. ③经过扩散得到最终加密图像.这样就没有了文献[11]中位平面置乱时的分组限制, 加密效果良好.经实验分析可知, 本文提出的图像加密算法能够有效地降低相邻像素之间的相关性, 有效增强抵抗选择明文攻击和已知明文攻击的能力, 最终的加密图像像素分布均匀.
1 算法原理 1.1 混沌系统混沌是非线性动力系统的固有特性, 是普遍存在于非线性系统中的现象.混沌系统的伪随机性、遍历性和初值敏感性等特点, 促使它在加密领域被引起广泛的关注.本文用到了以下混沌系统.
(1) Tent混沌系统, 方程为
| $ \begin{align} x_{n+1} =\left\{ {{\begin{array}{*{20}} {\mu x_n , } \hfill & {0<x_n <\dfrac{1}{2}, } \hfill \\ {\mu (1-x_n ), } \hfill & \dfrac{1}{2}\le x_n <1, \hfill \\ \end{array} }} \right. \end{align} $ | (1) |
其中,
(2) Henon混沌系统, 方程为
| $ \begin{align} \left\{ {{\begin{array}{*{20}} {x_{n+1} =1-ax_n^2 +y_n , } \\ {y_{n+1} =bx_n }, \end{array} }} \right. \end{align} $ | (2) |
是一个二维的离散动力系统.公式(2)中,
| $ \begin{align} \left\{ {{\begin{array}{*{20}} {x_{n+1} =1-ax_n^2 +y_n \bmod N, } \\ {y_{n+1} =bx_n +c\bmod N, } \end{array} }} \right. \end{align} $ | (3) |
其中,
| $ \begin{align} \left\{ {{\begin{array}{*{20}} {x_n =y_{n+1} -c\bmod N, } \\ {y_n =x_{n+1} -1+ax_n^2 \bmod N.} \end{array} }} \right. \end{align} $ | (4) |
使用Tent映射系统可以产生一维的混沌序列, 或称为密钥流. Henon映射系统可以用作坐标变换, 用于对像素置乱的过程中.
1.2 算法特性在Henon映射中有
在对加密效果的评价中, 像素个数变化率(Number of Pixels Change Rate, NPCR)是表示当明文图像的某个像素发生改变时, 经过加密得到的密文图像与由加密原文图像得到的密文图像的像素变化率.实际上, 像素个数变化率描述的是加密算法对明文变化的敏感性, 详细内容将在第2.5节讨论.讨论像素个数变化率的目的在于, 如果采用某些攻击方法, 如选择明文攻击和已知明文攻击, 来攻击加密算法, 攻击者可以选择一定数量的特定明文图像和对应密文图像, 通过发现其中的规律以破解加密算法所采用的密钥.因此, 理想的加密算法要对明文具有足够的敏感性.上述的敏感性至少要满足两个基本要求: ①如果某个像素点的值发生变化, 则加密过程会不同; ②如果没有像素点的值发生变化, 但是任意两个或多个像素点的位置发生了交换或变化而其他点保持不变, 则加密过程也会不同.
综上, 在确定Tent映射系统中的控制参数时, 既需考虑明文图像中每个像素点的像素值, 又要考虑像素点的位置信息.
1.3 加密原则基于像素层面的加密算法的效果不够理想.因此, 目前越来越多的研究都是基于比特位层面的加密[1-3, 10-11].灰度图像通常只有一个道, 且像素值的取值范围为[0, 255].所以对于数字灰度图像, 如果把所有像素值都用二进制表示, 那么这些0和1因为位置的不同, 所携带的信息量也不同, 具体第
| $ \begin{align} p(i)=\frac{2^{i-1}}{\sum\limits_{j=0}^7 {2^j} }, \mbox{ }i=1, \mbox{ 2}, \mbox{ }\cdots, 8 \end{align} $ | (5) |
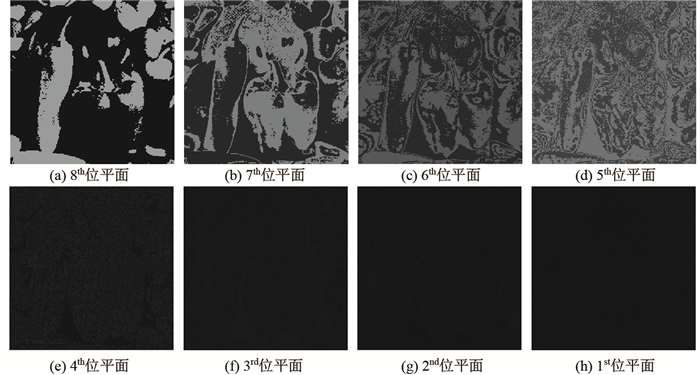
来计算[11].根据式(5)可知, 高位携带的信息更多一些. 图 1所示是一张图像的每一位所组成的图像, 其中图 1(a)-图 1(h)分别对应由像素值第8, 7,
|
图 1 不同位平面所携带的信息 Fig.1 Information carried by the different bit planes |
有研究表明, 达到理想的加密效果需要改变的比特位的数目只占全部比特位的3.3%[11].因为图像普遍存在着局部分布不均匀的问题, 所以加密的目标重点并非尽量多地改变数据, 而是尽量改变数据的分布, 使其均匀.因此, 为了权衡加密效果和算法开销, 算法应注重改变图像数据的分布.
1.4 图像加密算法基于以上分析, 本文提出了如下加密算法, 具体步骤为如下.
(1) 对于一幅大小为
| $ \begin{align} \left\{ {{\begin{array}{*{20}} S=\sum\limits_{i, j} {P_{ij} \otimes {i}'\otimes {j}'} , \\ {i}'=i\bmod 256, \\ {j}'=j\bmod 256, \end{array} }} \right. \end{align} $ | (6) |
| $ \mu =\alpha \times 2^{\frac{S}{N\times N\times 256}}, $ | (7) |
| $ k=S\bmod10^3+10^3, $ | (8) |
其中,
(2) 将图像中每一个像素值都用8位二进制表示, 由
(3) 用bit1异或bit5, 对其他位平面也做同样对应的操作, 可形式化地表示为
| $ \begin{align} \mathrm {bit}_j =\mathrm {bit}_j \otimes \mathrm {bit}_{j-4} , \quad j=5, 6, 7, 8, \end{align} $ | (9) |
这是自适应操作的过程.位平面之间的异或是指两位平面中对应点的像素值进行异或运算.
(4) 输入密钥
(5) 对Tent系统再迭代3次, 得到3个实数value1, value2, value3, 利用式(10)-(12)计算
| $ a_i ={\rm floor(value}_i \times 10^3)\bmod 250+5, $ | (10) |
| $ c_i ={\rm floor(value}_i \times 10^6)\bmod 250+5, $ | (11) |
| $ k_i ={\rm floor(value}_i \times 10^7)\bmod 5+1, $ | (12) |
其中,
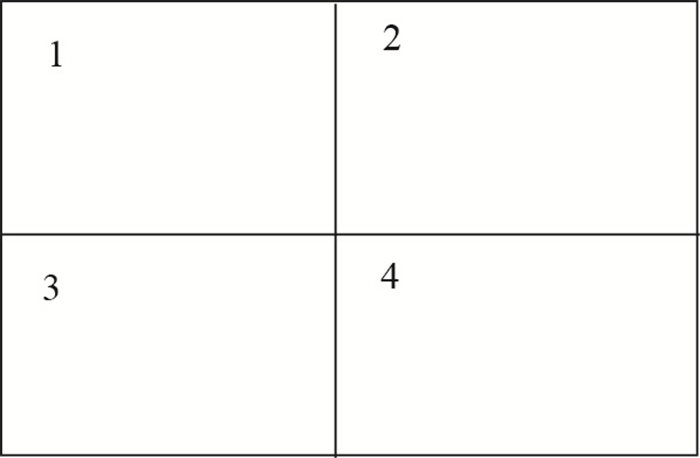
(6) 将bit5, bit6, bit7, bit8分别放置到对应的方框1, 2, 3, 4中, 如图 2所示.由此形成了一个2
|
图 2 位平面的重组放置方式 Fig.2 Reorganized placement of the bit planes |
(7) 继续对Tent映射系统迭代8次, 得到
| $ \begin{equation} P_j^\mathrm T =P_{p[i]}^\mathrm T =T_i =t_i , \quad i=1, 2, \cdots, 8, \end{equation} $ | (13) |
则
| $ \begin{align} R_{p[i]} =B_i =\mathrm {bit}_i , \quad i=1, 2, \cdots, 8, \end{align} $ | (14) |
显然
(8) 从上述步骤可知,
(9) 继续对Tent映射系统迭代
| $ P'[i] = \left\{ \begin{array}{l} P[i] \otimes {S_0}, \;\;\;\;\;i = 1, \\ P[i] \otimes (P'[i - 1] + I[i]) \otimes I[i], \quad i > 1, \end{array} \right. $ | (15) |
其中, 加法为模256下的同余加法,
|
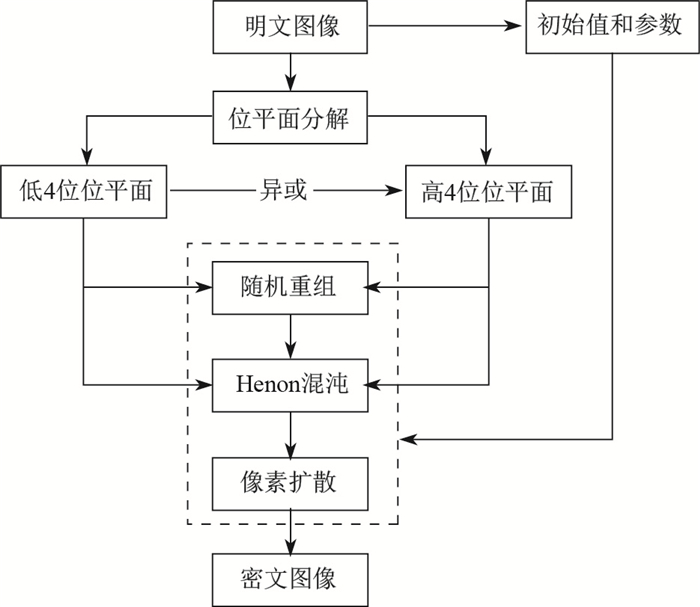
图 3 图像加密过程 Fig.3 Diagram of the image encryption process |
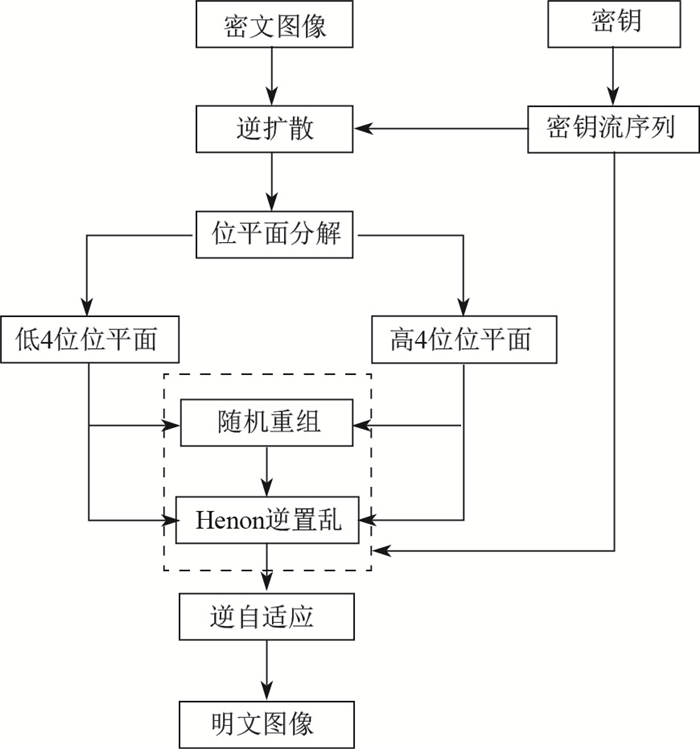
加密算法中每一步均可逆, 故解密算法是加密算法的逆过程.图像解密的流程如图 4所示.
|
图 4 图像解密过程 Fig.4 Diagram of the image decryption process |
加密过程中的密钥有
(1) 设密文大小为
(2) 通过对系统进行迭代得到实数value1, value2, value3, 实数序列
(3) 将密文图像按行优先展开为一维序列
| $ \begin{align} P[i]=\left\{ \begin{array}{l} P'[i]\otimes I[i]\otimes (P'[i-1]+I[i]), \quad i>1, \\ P'[i]\otimes S_0 , \quad i=1, \end{array} \right. \end{align} $ | (16) |
得到中间密文
(4) 将中间密文
(5) 自适应过程的逆过程, 即对于位平面进行一次式(9)的计算, 可得到原明文图像的位平面, 然后将8个位平面按正常顺序重组, 将每个像素点的8个01位表示转换成十进制数即得到最终的解密图像.
2 实验结果和性能分析仿真实验的明文图像为灰度图像Peppers, 大小为

|
图 5 明文图像、密文图像和解密图像 Fig.5 Plain image, cipher image, and decrypted image |
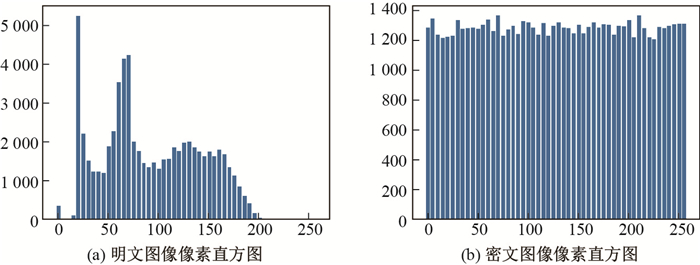
像素分布直方图能直观地揭示图像中的像素值分布.明文图像的像素值一般会分布不均, 攻击者可以利用统计特性攻击来获得图像中的有用信息; 而密文图像使得攻击者难以从中得到有价值的信息.密文图像中的像素分布越均匀, 则加密算法越理想.图像Peppers的明文和密文的像素分布直方图如图 6所示.
|
图 6 明文图像和密文图像的像素分布直方图 Fig.6 Histogram of plain image and cipher image pixels |
理想的加密算法需要降低明文图像中相邻像素间的强相关性, 该相关性可由相关系数定量描述.计算图像相关系数的方法为, 在图像中随机选取10 000个像素点存入
| $ \begin{align} \rho _{x, y} =\frac{E\{[x-E(x)][y-E(y)]\}}{\sqrt {D(x)} \sqrt {D(y)} }, \end{align} $ | (17) |
其中,
| $ E(x)=\frac{1}{n}\sum\limits_{i=1}^n {x_i } , $ | (18) |
| $ D(x)=\frac{1}{n}\sum\limits_{i=1}^n {[x_i -E(x)]^2} . $ | (19) |
在二维数字图像中, 图像的相邻关系包括:水平、垂直、对角这3种. 表 1所示为不同加密算法的明文图像和密文图像的相关性分析结果.
| 表 1 不同加密方法的相关性比较 Tab. 1 Correlation comparison between different encryption methods |
由表 1可知, 密文图像的相关系数的绝对值非常接近于0.这也定量地说明了密文像素的弱相关性.通过比较, 本文算法相关性方面的表现要优于其他文献中的加密算法.
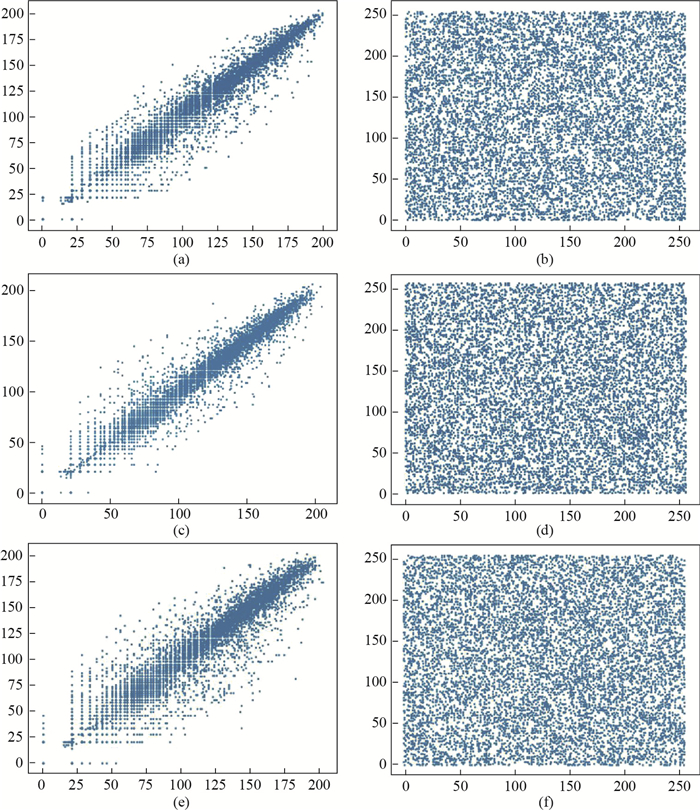
除了利用相关系数表示之外, 以相邻两点的像素值分别作为横、纵坐标描绘出散点图, 该散点图也可以将其相关性直观地展示出来, 如图 7所示. 图 7(a)、图 7(c)和图 7(e)分别是明文图像中具有水平、垂直和对角关系的相邻像素形成的散点图, 而与其对应的密文图像的散点图分别为图 7(b)、图 7(d)和图 7(f).从图 7中可知, 明文图像的相邻像素之间有明显的相关性, 而对于密文图像, 散点图中的点分布均匀, 毫无规律, 表明本文加密算法对破坏相关性有良好的表现.
|
图 7 相邻像素散点图 Fig.7 Adjacent pixel scatter plots |
借助信息熵的概念能定量地描述图像像素的混乱程度和分布情况.设
| $ \begin{equation} \label{eq7} H(X)=-\sum\limits_{i=1}^n {p(x_i )\log _2 p(x_i )} , \end{equation} $ | (20) |
其中,
由信息熵的表达式
| 表 2 明文图像和密文图像的熵值 Tab. 2 Information entropy of plain image and cipher image |
密钥敏感性表示在密钥发生改变时密文所对应的变化程度.计算密钥敏感性常采用的方法是让密钥的数值发生很微小的变化, 并计算两次加密的不同密文的差异, 这种差异称作灰度均方差.灰度均方差的计算公式为
| $ \begin{align} E_{C, {C}'} =\frac{1}{m\times n}\sum\limits_{i=1}^m {\sum\limits_{j=1}^n {(C_{ij} -{C}'_{ij} )^2} }, \end{align} $ | (21) |
其中,
| 表 3 灰度均方差 Tab. 3 Gray mean square error |
在表 3中,
采用明文敏感性分析能够定量地评估明文图像发生微小变化对密文图像的影响.明文敏感性分析方法主要包括像素个数变化率(NPCR)和归一化平均变化强度(Unified Average Changing Intensity, UACI).
(1) NPCR的计算公式为
| $ \begin{align} \mbox{NPCR}=\frac{\sum\limits_{i, j} {D(i, j)} }{m\times n}\times 100\% , \end{align} $ | (22) |
其中
| $ \begin{align} \label{eq8} D(i, j)=\left\{ {{\begin{array}{*{20}} 1, \quad C_1 (i, j)\ne C_2 (i, j), \\ 0, \quad C_1 (i, j)=C_2 (i, j), \end{array} }} \right. \end{align} $ | (23) |
其中,
(2) UACI的计算公式为
| $ \begin{align} \mbox{UACI}=\frac{1}{m\times n}\sum\limits_{i, j} {\frac{\vert C_1 (i, j)-C_2 (i, j)\vert }{255}} \times 100\% . \end{align} $ | (24) |
对于不同的图像, 通过随机修改某一像素点得到新的明文图像, 并对其加密得到密文图像, 最后计算其NPCR和UACI, 结果如表 4所示. 表 4的实验结果可表明, 本文加密算法对明文信息变化敏感, 并能有效抵抗差分攻击.
| 表 4 NPCR和UACI Tab. 4 NPCR and UACI performance |
密钥空间是衡量加密算法是否能够抵抗穷举攻击的指标, 密钥空间足够大才能抵御穷举攻击.本文加密算法中的密钥包括用于产生混沌序列的初值
本文所提出的图像加密算法是基于比特位层面的加密, 并且置乱是全局的, 因此能有效破坏图像数据分布的局部不均匀性.同时, 本文算法中加入了自适应过程, 给一些攻击行为, 如选择明文攻击等, 带来了更大的挑战, 并且增强了加密算法的明文敏感性.实验数据表明, 本文算法打破了其他基于像素层面的加密算法和基于比特位层面的局部固定置乱的加密算法的局限, 相比于其他算法获得了更好的效果.本文分别从NPCR、UACI、信息熵、明文敏感性等角度对所提算法进行了测试实验, 结果显示, 该加密算法都有更好的表现.因此, 本文提出的加密算法有更高的安全性和较好的应用前景.
| [1] |
ZHU Z L, ZHANG W, WONG K W, et al. A chaos-based symmetric image encryption scheme using a bit-level permutation[J]. Information Sciences, 2011, 181(6): 1171-1186. DOI:10.1016/j.ins.2010.11.009 |
| [2] |
WONG K W, KWOK B S H, LAW W S. A fast image encryption scheme based on chaotic standard map[J]. Physics Letters A, 2008, 372(15): 2645-2652. DOI:10.1016/j.physleta.2007.12.026 |
| [3] |
ALVAREZ G, LI S. Some basic cryptographic requirements for chaos-based cryptosystems[J]. International Journal of Bifurcation and Chaos, 2006, 16(8): 2129-2151. DOI:10.1142/S0218127406015970 |
| [4] |
ABDULLAH A H, ENAYATIFAR R, LEE M. A hybrid genetic algorithm and chaotic function model for image encryption[J]. AEU-International Journal of Electronics and Communications, 2012, 66(10): 806-816. DOI:10.1016/j.aeue.2012.01.015 |
| [5] |
WANG Y, WONG K W, LIAO X F, et al. A chaos-based image encryption algorithm with variable control parameters[J]. Chaos, Solitons & Fractals, 2009, 41(4): 1773-1783. |
| [6] |
YANG H Q, LIAO X F, WONG K W, et al. A new block cipher based on chaotic map and group theory[J]. Chaos, Solitons & Fractals, 2009, 40(1): 50-59. |
| [7] |
WANG Y, WONG K W, LIAO X F, et al. A new chaos-based fast image encryption algorithm[J]. Applied Soft Computing, 2011, 11(1): 514-522. DOI:10.1016/j.asoc.2009.12.011 |
| [8] |
汪彦, 涂立. 基于改进Lorenz混沌系统的图像加密新算法[J]. 中南大学学报(自然科学版), 2017, 48(10): 2678-2685. DOI:10.11817/j.issn.1672-7207.2017.10.017 |
| [9] |
毛骁骁, 孙克辉, 刘文浩. 基于分数阶统一混沌系统的图像加密算法[J]. 传感器与微系统, 2017, 36(6): 138-141. |
| [10] |
PING P, LI J H, MAO Y C, et al. Image encryption algorithm based on chaotic maps and bit reconstruction[J]. Journal of Image and Graphics, 2017, 22(10): 1348-1355. |
| [11] |
ZHANG W, WONG K W, YU H, et al. A symmetric color image encryption algorithm using the intrinsic features of bit distributions[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(3): 584-600. DOI:10.1016/j.cnsns.2012.08.010 |




