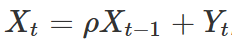This paper deals with the Monte Carlo Simulation in a Bayesian framework. It shows the importance of the use of Monte Carlo experiments through refined descriptive sampling within the autoregressive model , where 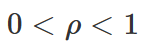and the errors Yt are independent random variables following an exponential distribution of parameter θ. To achieve this, a Bayesian Autoregressive Adaptive Refined Descriptive Sampling (B2ARDS) algorithm is proposed to estimate the parameters ρ and θ of such a model by a Bayesian method. We have used the same prior as the one already used by some authors, and computed their properties when the Normality error assumption is released to an exponential distribution. The results show that B2ARDS algorithm provides accurate and efficient point estimates.

References

• Albert, J. H., & Chib, S. (1993). Bayes inference via Gibbs sampling of autoregressive time series subject to Markov mean and variance shifts. Journal of Business && Economic Statistics, 11(1), 1–15. 
• Aloui, A., Zioui, A., Ourbih-Tari, M., & Alioui, A. (2015). A general purpose module using refined descriptive sampling for installation in simulation systems. Computational Statistics, 30(2), 477–490. https://doi.org/10.1007/s00180-014-0545-7 
• Amaral Turkmann, M. A. (1990). Bayesian analysis of an autoregressive process with exponential white noise. Statistics, 21(4), 601–608. https://doi.org/10.1080/02331889008802270 
• Andel, J. (1988). On AR(1) processes with exponential white noise. Communications in Statistics - Theory and Methods, 17(5), 1481–1495. http://doi.org/10.1080/03610928808829693 
• Ashby, D. (2006). Bayesian statistics in medicine: A 25 year review. Statistics in Medicine, 25(21), 3589–3631. https://doi.org/10.1002/sim.v25:21 
• Baghdali-Ourbih, L., Ourbih-Tari, M., & Dahmani, A. (2017). Implementing refined descriptive sampling into three phase discrete-event simulation models. Communications in Statistics : Simulation and Computation. Taylor and Francis, 46(5), 4035–4049. https://doi.org/10.1080/03610918.2015.1085557 
• Barnett, G., Koln, R., & Sheather, S. (1996). Bayesian estimation of an autoregressive model using Markov chain Monte Carlo. Journal of Econometrics, 74(2), 237–254. https://doi.org/10.1016/0304-4076(95)01744-5
• Beaumont, M. A., & Rannala, B. (2004). The Bayesian revolution in genetics. Nature Reviews Genetics, 5(4), 251–261. https://doi.org/10.1038/nrg1318 
• Boubalou, M., Ourbih-Tari, M., Aloui, A., & Zioui, A. (2019). Comparing M/G/1 queue estimators in Monte Carlo simulation through the tested generator getRDS and the proposed getLHS using variance reduction. Monte Carlo Methods and Applications, 25(2), 177–186. https://doi.org/10.1515/mcma-2019-2033
• Box, G., Jinkins, G., & Reinsel, G. (1976). Time series analysis: Forecasting and control. John Wiley and Sons. 
• Corander, J. (2006). Is there a real Bayesian revolution in pattern recognition for bioinformatics. Current Bioinformatics, 1(2), 161–165. https://doi.org/10.2174/157489306777011932 
• Diaz, J., & Farah, J. (1981). Bayesian identification of autoregressive processes. In Proceedings of the S.L, 22nd NBER-NSF. Seminar on Bayesian inference in econometrics. 
• Geweke, J. (1999). Using simulation methods for Bayesian econometric models. Inference, Development, and Communication Econometric Reviews, 18(1), 1–126. https://doi.org/10.1080/07474939908800428 
• Ghosh, M., & Heo, J. (2003). Default Bayesian priors for regression models with first-order autoregressive residuals. Journal of Time Series Analysis, 24(3), 269–282. https://doi.org/10.1111/jtsa.2003.24.issue-3 
• Ibazizen, M., & Fellag, H. (2003). Bayesian estimation of an AR(1) process with exponential white noise. Journal of Theoretical and Applied Statistics, 37(5), 365–372. https://doi.org/10.1080/0233188031000078042 
• Idjis, K., Ourbih-Tari, M., & Baghdali-Ourbih, L. (2017). Variance reduction in M/M/1 retrial queues using refined descriptive sampling. Communications in Statistics – Simulation and Computation, 46(6), 5002–5020. https://doi.org/10.1080/03610918.2016.1140778 
• Keller, A., Heinrich, S., & Niederreiter, H. (2008). Monte Carlo and quasi Monte Carlo methods. Springer.
• Kumar, J., & Agiwal, V. (2019). Bayesian estimation for fully shifted panel AR(1) time series model. Thai Journal of Mathematics, 17, 167–183. https://thaijmath.in.cmu.ac.th 
• Loh, W. L. (1996). On latin hypercube sampling. Annals of Statistics, 24(5), 2058–2080. https://doi.org/10.1214/aos/1069362310 
• Marriot, J., & Smith, A. (1992). Reparametrization aspects of numerical Bayesian methods for autoregressive moving average models. Journal of Time Series Analysis, 13(4), 307–331. https://doi.org/10.1111/j.1467-9892.1992.tb00111.x 
• Mckay, M. D., Conover, W. J., & Beckman, R. J. (1979). A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics, 21(2), 239–245. https://doi.org/10.2307/1268522 
• Monahan, J. (1984). Fully Bayesian analysis of ARMA time series models. Journal of Econometrics, 21(3), 307–331. https://doi.org/10.1016/0304-4076(83)90048-9 
• Ourbih-Tari, M., & Azzal, M. (2017). Survival function estimation with non parametric adaptative refined descriptive sampling algorithm : A case study. Communication in Statistics-Theory and Methods, 46(12), 5840–5850. https://doi.org/10.1080/03610926.2015.1065328 
• Ourbih-Tari, M., Zioui, A., & Aloui, A. (2017). Variance reduction in the simulation of a stationary M/G/1 queuing system using refined descriptive sampling. Communication in Statistics-Simulation and Computation, 46(5), 3504–3515. https://doi.org/10.1080/03610918.2015.1096374 
• Pereira, I., & Amaral-Turkman, M. A. (2004). Bayesian prediction in threshold autoregressive models with exponential white noise. sociedad De Estadistica E Investigacion Operativa, 13(1), 45–64. https://doi.org/10.1007/BF02603000 
• Saliby, E. (1990). Descriptive sampling: A better approach to Monte Carlo simulation. Journal of the Operational Research Society, 41(12), 1133–1142. https://doi.org/10.1057/jors.1990.180 
• Smith, A. F. M., & Robert, G. O. (1993). Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods. Journal of the Royal Statistical Society, 5(5), 3–23. https://doi.org/10.1111/j.2517-6161.1993.tbo1466.X 
• Stein, M. (1987). Large sample properties of simulations using latin hypercube sampling. Technometrics, 29(2), 143–151. https://doi.org/10.1080/00401706.1987.10488205
• Suparman, S., & Rusiman, M. S. (2018). Hierarchical Bayesian estimation for stationary autoregressive models using reversible jump MCMC algorithm. International Journal of Engineering && Technology, 7(430), 64–67. https://eprints.uthm.edu.my/id/eprint/5110 
• Tamiti, A., Ourbih-Tari, M., Aloui, A., & Idjis, K. (2018). The use of variance reduction, relative error and bias in testing the performance of M/G/1 retrial queues estimators in Monte Carlo simulation. Monte Carlo Methods and Applications, 24(3), 165–178. https://doi.org/10.1515/mcma-2018-0015
• Tari, M., & Dahmani, A. (2005a). Flowshop simulator using different sampling methods. Operational Research, 5(2), 261–272. https://doi.org/10.1007/BF02944312 
• Tari, M., & Dahmani, A. (2005b). The three phase discrete event simulation using some sampling methods. International Journal of Applied Mathematics and Statistics, 3(5), 37–48.
• Tari, M., & Dahmani, A. (2006). Refined descriptive sampling: A better approach to Monte Carlo simulation. Simulation Modelling: Practice and Theory, 14(2), 143–160. https://doi.org/10.1016/j.simpat.2005.04.001

To cite this article: Djoweyda Ghouil & Megdouda Ourbih-Tari (2023) Bayesian autoregressive adaptive refined descriptive sampling algorithm in the Monte Carlo simulation, Statistical Theory and Related Fields, 7:3, 177-187, DOI: 10.1080/24754269.2023.2180225

To link to this article: https://doi.org/10.1080/24754269.2023.2180225