Fig.1

The configuration of two diatomic polar molecules in an external electric field"

Fig.2

Stark state eigenenergies of the polar diatomic molecules for different $\mu \varepsilon / B$ values "

Fig.3

The relationship between the coefficients corresponding to spherical harmonic function, $ {a_j} $ and $ {b_j} $ , and $\mu \varepsilon / B$ for each of the qubit basis states, $ \left| 0 \right\rangle $ and $ \left| 1 \right\rangle $ "

Fig.4

Schematic diagram showing the relationship between values of molecular orientation, $ {C_0} $ and $ {C_1} $ , and the transition dipole moment, $ {C_X} $ , with $\mu \varepsilon / B$ "

Fig.5

Schematic diagram of a one-dimensional molecular chain consisting of N polar molecules "

Fig.6

The relationship between the pairwise concurrence ${C_{12}}$ of a one-dimensional molecular chain system consisting of $ N $ molecules and ${\varOmega \mathord{\left/ {\vphantom {\varOmega B}} \right. } B}$ , at different temperatures "

Fig.7

The relationship between the pairwise concurrence ${C_{12}}$ of a one-dimensional molecular chain system consisting of $ N $ molecules and $ {{\mu \varepsilon } \mathord{\left/ {\vphantom {{\mu \varepsilon } B}} \right. } B} $ , at different temperatures "

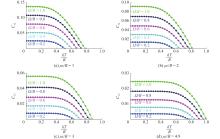
Fig.8

The relationship between the pairwise concurrence $ {C_{12}} $ of a one-dimensional molecular chain system and $ {{kT} \mathord{\left/ {\vphantom {{kT} B}} \right. } B} $ , for different values of ${\varOmega \mathord{\left/ {\vphantom {\Omega B}} \right. } B}$ , $ {{\mu \varepsilon } \mathord{\left/ {\vphantom {{\mu \varepsilon } B}} \right. } B} $ "

Fig.9

The relationship between the pairwise concurrence of pendular states formed by the first molecule and any other molecule in a one-dimensional chain system of $ N = 8 $ and $ {{\mu \varepsilon } \mathord{\left/ {\vphantom {{\mu \varepsilon } B}} \right. } B} $ at different temperatures "

Fig.10

The relationship between global entanglement and $ {{\mu \varepsilon } \mathord{\left/ {\vphantom {{\mu \varepsilon } B}} \right. } B} $ for a one-dimensional molecular chain system consisting of $ N $ molecules "

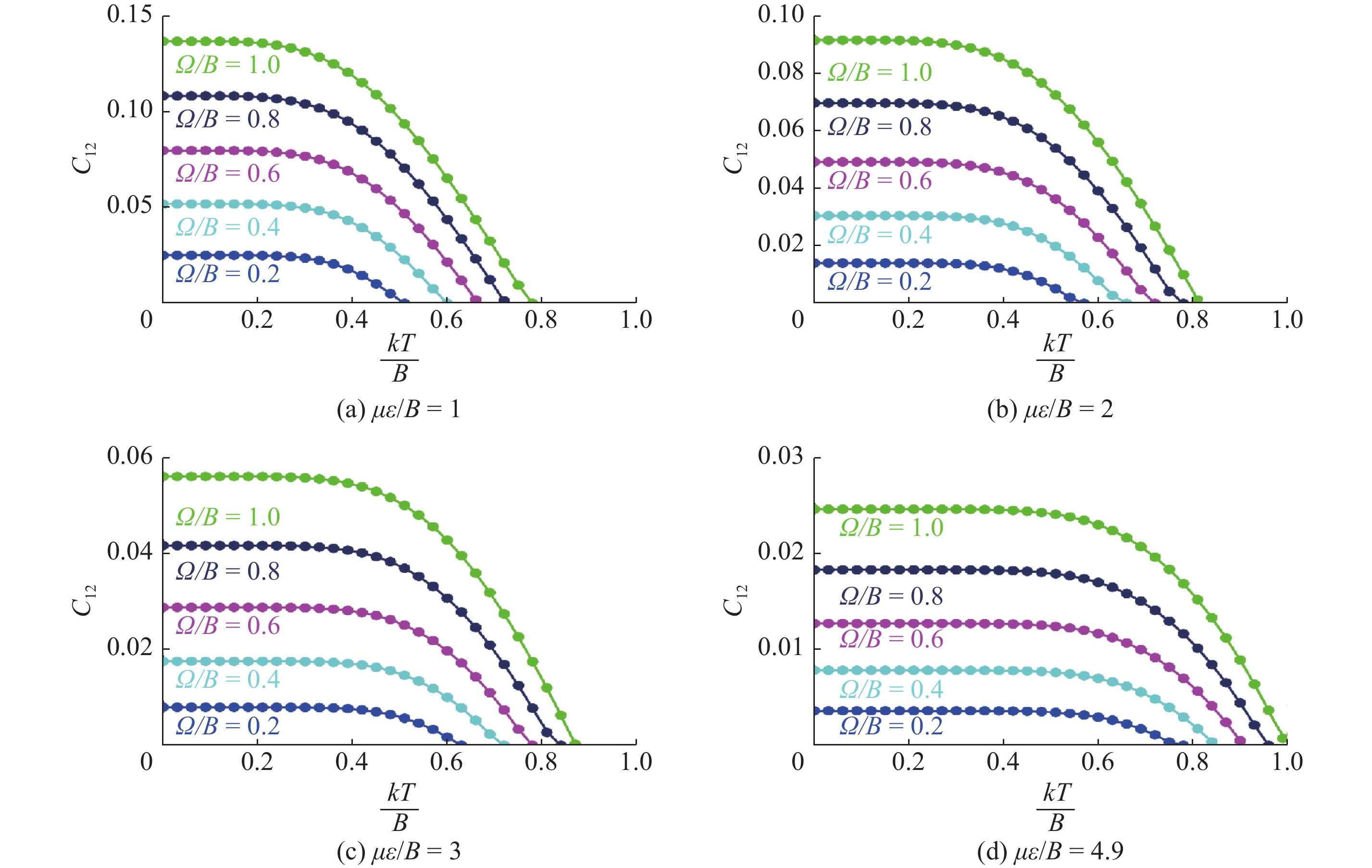
Fig.11

The relationship between global entanglement and ${\varOmega \mathord{\left/ {\vphantom {\varOmega B}} \right. } B}$ for a one-dimensional molecular chain system consisting of $ N $ molecules, with different values of $ {{\mu \varepsilon } \mathord{\left/ {\vphantom {{\mu \varepsilon } B}} \right. } B} $ "

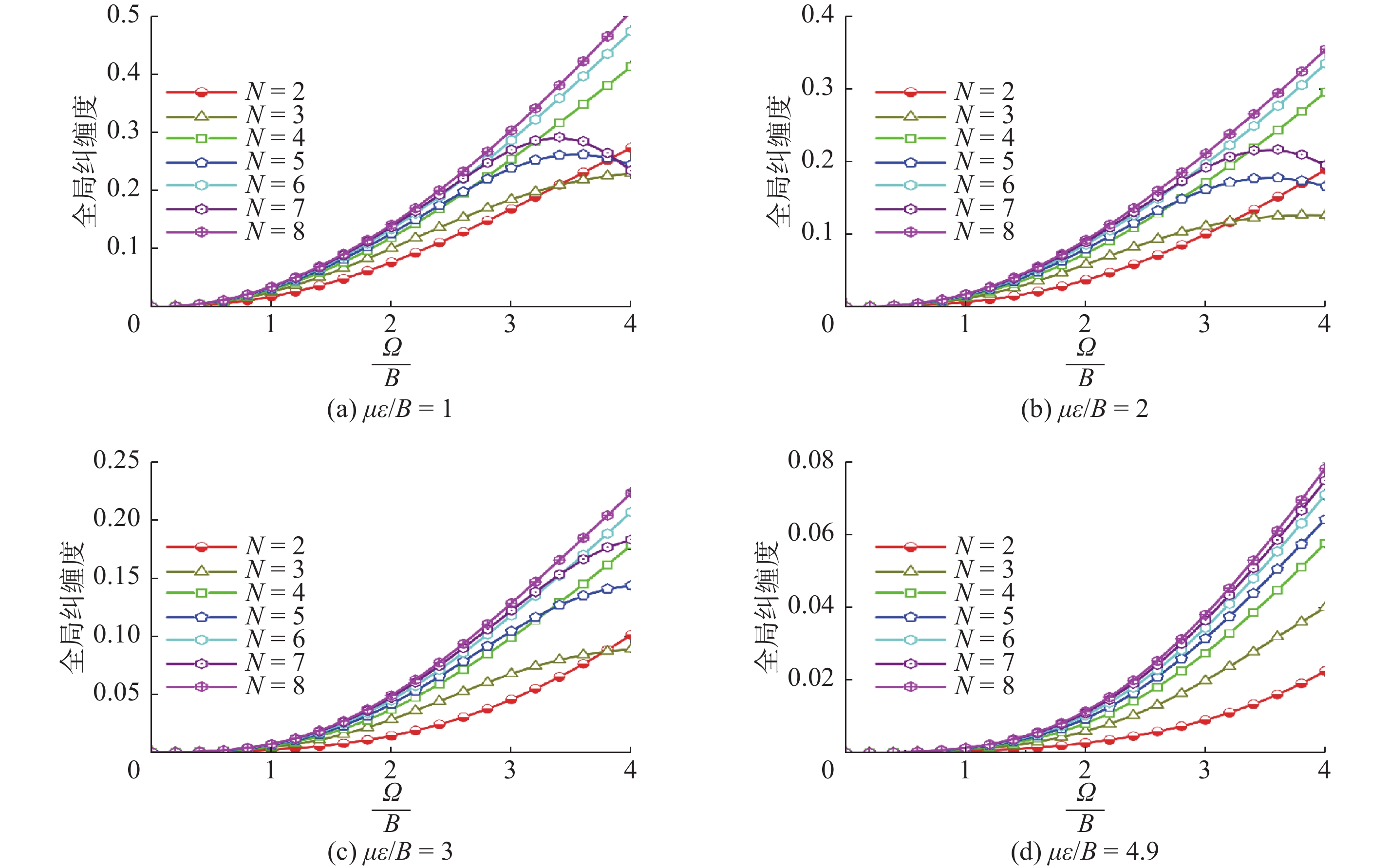
Fig.12

Global entanglement as a function of molecular number $ N $ for one-dimensional molecular chain systems with different values of ${\varOmega \mathord{\left/ {\vphantom {\varOmega B}} \right. } B}$ and ${{\mu \varepsilon } \mathord{\left/ {\vphantom {{\mu \varepsilon } B}} \right. } B} $ "